
 |
| Elliott Sound Products | Electronics Maths Functions |
 Main Index Main Index  Articles Index Articles Index |
Before calculators and computers, many mathematical functions were performed using operational amplifiers. They got that name because they can provide operational functions, such as addition, subtraction and comparison. They are now commonplace, and are generally just called 'op-amps' or 'opamps'. They revolutionalised many mathematical computations, as they could come up with an answer very quickly - much faster than people could manage.
Very early 'computations' used mechanical means, but these must be (almost by definition) complex and delicate. Possibly the most well-known is the Babbage 'analytical (aka 'difference') engine', which was eventually completed by Ada Lovelace (Charles Babbage never got it working). There's a mountain of information on-line, and I don't propose adding even more. However, one can but marvel at the ingenuity and skill of these early pioneers of computing. Most of these early devices were never commercialised, although several well known (but not necessarily still operational) companies started life selling 'adding machines' (sometimes referred to as 'comptometers' although they are a separate class of mechanical computer). For more info, see Adding Machine (Wikipedia).
Naturally, prior to the introduction of mechanical means, all maths were performed by the normal (human derived) processes of multiplication, division, addition and subtraction. Complex problems required great skill (and a lot of paper). The basis of maths as we know it is ancient, with some quite advanced methods developed to solve 'difficult' equations. Things we now consider to be trivial (e.g. square roots) had mathematicians of old trying to come up with the most elegant solution. It's educational to do a web search to see some of the history behind the maths we use today.
The subject of this article is the calculation of mathematical problems using analogue electronics. The simplest (by far) are addition and subtraction, which can be done very accurately using commonly available parts. More difficult are problems involving multiplication and division, and not only for electronic systems. These continue to be an issue for many people, and it has to be considered that there are people who are 'no good at maths' (often their own claim to avoid situations where they are expected to work out something). Don't expect to see quadratic equations, polynomials or other 'esoteric' maths constructs here - I've kept to the basics, so don't be scared off just yet. 
Note that I will always use the term 'maths' (plural) rather than the US convention of 'math' (there really is more than one type). That notwithstanding, I'll only be looking at relatively simple circuitry (and therefore simple equations), and I must stress that the circuits included have all been simulated, but not built and tested. There are some good reasons for this, with the main ones showing up where multiplication and division are involved. Without closely matched transistors, simple log/ antilog amplifiers will be wildly inaccurate.
Many functions use (or used) logs and antilogs, something that I suspect will cause many readers to shudder at the very thought. Fear not, while I do explain logs and antilogs, a complete understanding is not necessary to follow the general reasoning. Until I was able to afford a calculator (in ca. 1969 IIRC), I used log tables for most electronics calculations I performed because it was far easier than long division (in particular). I also used a slide rule (does anyone remember those?). I preferred log tables because I found them to be easier and more accurate.
Of all the functions, square roots were always one of the most troublesome. Early calculators could square easily, simply by multiplying the number by itself (e.g. 12 × 12 = 144). Attempting square roots with the early circuits was much harder. I challenge anyone with a good maths background to work out how to perform a square root. It seems simple enough on the surface, but when it comes down to the nitty-gritty (i.e. actually extracting the square root) it's likely to fall straight into the 'too hard' basket. It was always easy using log tables - just divide the logarithm of the number by two, then take the antilog. The simple method I often use with a calculator (particularly for other less common roots) is shown below.
For anyone interested, I recommend that you look at Calculate a Square Root by Hand (WikiHow.com). Daunting doesn't even come close when you have 'odd' or 'irrational' numbers (an irrational number cannot be expressed as the ratio of two integers - i.e. a simple fraction such as 1/4 or 5/8). I'm not about to provide a maths lesson here, but I do recommend that the reader looks into some of the concepts. I also won't cover 'complex' numbers (J-notation [j=√-1], aka the 'imaginary' part of a 'real' number).
Cube roots are uncommon for analogue processing systems, and this is good because they aren't very good at solving this type of problem. Calculators have many functions these days, and when you know how, you can perform most 'irksome' calculations with ease. Raising to a power '^' (may also be shown as xy or yx) is one such 'trick' that doesn't seem to be as well publicised as it should be. If it helps, you can take the nth root of a number ('X') with the formula ...
nth root = X ^( 1 / n ) A cube root is therefore ...
³√X = X ^(1/3) For example ...
³√123 = 123 ^(1/3) = 4.973189833
Why might you need these? If you know the internal volume of a speaker box, you can get the basic inside dimensions by taking the cube root of the volume in litres. The answer is in decimetres (1 decimetre = 100mm), so multiply by 100 to get millimetres. The final shape is determined by multiplying/ dividing the cube root by a suitable ratio (see Loudspeaker Enclosure Design Guidelines (Section 13) for the details.
Consider too that an octave has 12 semitones, logarithmically spaced between (say) A440 and A880. The 12th root of two is 1.059463094, and if you multiply that by itself 12 times, the answer is two. You've just re-created the equally tempered musical scale. It's not within the scope of this article, but it is nonetheless something useful to know (well, I think so anyway). This is how the distance between frets is calculated for a guitar.
Everything shown here can be worked out with a calculator, and for most of the complex circuits that's how I verified that the circuit was behaving as it should. There are some exceptions of course, in particular the calculation of RMS from a non-sinusoidal and/ or asymmetrical waveform. However, if you follow the general idea through, hopefully it will make sense. These are not audio circuits for the most part, but the concepts are used in some audio circuitry. VCAs (voltage controlled amplifiers) are a case in point, especially those with a logarithmic response to the control signal (typically measured in dB/mV).
If you simulate these circuits shown, you may or may not be able to duplicate my results. Simulators from different vendors need different 'tricks' to make them work with odd circuitry (these definitely qualify). I use SIMetrix (Release 6.20d), and others will behave differently. The opamps were supplied with ±15V for all circuits unless otherwise noted, and supply bypass caps are not shown (they are essential for any real circuit).
You can be forgiven for thinking that analogue computing is no longer relevant. However, you'd be wrong, as there's a current resurgence in interest from academia and IC manufacturers. Just as I thought this article was almost complete, I received an industry email with an interesting story and a link to a startup (Mythic) extolling the virtues of analogue processing. It turns out that many of the major IC makers are also looking in the same direction, with an analogue front-end used for its speed, followed by digital processing to get the best accuracy. For example, if you were to read up on successive approximation ADCs you'd find that there can be many processing steps to get the answer. If an approximate answer is provided as the starting point, the number of steps can be dramatically reduced, saving time and reducing power.
An example is The Analog Thing (THAT). The design featured has a collection of the circuits described below, including integrators, summing amps, comparators and multipliers. There are also pots (potentiometers) to provide inputs, a patch panel to configure the processes and a panel meter to display results. There's a hybrid port to allow digital configuration, and 'master/minion' (aka 'master/slave') ports to allow multiple THATs to be daisy-chained for more computing power.
I expect this to be the beginning of a 'new era' of analogue computing, as researchers are looking at using analogue front-ends to AI (artificial intelligence) processors and many other processor intensive applications. Analogue processing can be very fast, while consuming modest power. Things like integration are difficult on a digital processor, but are dead easy with an opamp, a resistor and a capacitor. The same goes for differentiation. An analogue multiplier is blindingly fast, with some designed to operate at 100MHz or more. The same thing done digitally requires significant processing, which increases with the complexity of the numbers - integers are easy, floating-point 64-bit numbers far less so.
We can expect to see many more systems that use a hybrid analogue/ digital architecture in the coming years. The precision of digital isn't always necessary, and the speed of analogue may more than compensate for 'real world' applications. We have come to expect numbers to be accurate to 6 or more decimal places, because that's what we get from calculators. We very rarely need (or use) all those decimal places, and no-one will calculate a particular frequency to more than a couple of decimal places, and usually less.
Some of the examples shown have passed their 'best-before' date, in particular log/ antilog circuits. These were never particularly accurate, and even simulations (which have perfectly matched transistors and exact resistors and capacitors) have errors of more than 1%. It's usually impossible (or close to it) to set up an analogue computer to duplicate a calculation made previously, because of component tolerances, thermal drift and the effects of external noise (for example). However, when used appropriately, this won't matter at all if it allows a complex calculation to be performed to an 'acceptable' accuracy. No-one would expect to be able to calculate the trajectory of an artillery shell to the millimetre (for example), because the atmospheric conditions prevailing will have an effect that simply cannot be calculated (especially wind speed and direction).
The current focus appears to be on improving AI (artificial intelligence) techniques by using analogue processing in conjunction with digital analysis. The aim is to reduce the power needed (in watts) to compute the front-end system's responses to external stimuli (vision in particular), much of which is currently handled by power-hungry GPUs (graphic processing units). These feature massively parallel architecture to perform complex calculations. By using an analogue front-end, it is theoretically possible to reduce consumption from 100W or more to less than 10W.
Somewhat predictably, this is not something I will cover, other than this brief introduction. I suggest that if you are interested, do a web search, as there's a vast amount of information available. It's up to the reader to determine the usefulness of the information found - not all of it is likely to be accurate, and much of what I have seen is in general terms only. Most companies aren't about to reveal their trade secrets.
There are countless applications in electronics where we need to know if an input signal is 'greater than' or 'less than' a reference level. The absolute input level is usually not so important, but if the reference voltage is passed (in either direction), an indication is required. These can be set up to be very precise, and operation is generally assured if the input voltage is greater/ less than the reference voltage by only a few millivolts. Examples include clipping indicators (the signal voltage has exceeded the maximum/ minimum allowed), 'successive approximation' analogue to digital converters (ADCs) as used in many digital multimeters, or battery circuits where we need to stop charging above a preset voltage or disconnect the load if the voltage has fallen below a preset minimum.
Analogue Class-D amplifiers use a comparator to generate the PWM signal, and industrial processes use them for monitoring temperature, pressure, and many other processes that require on-off control (which may be many times per second). They are also used for lamp dimming (leading or trailing edge), heater/ oven temperature control and motor speed control. The device used for these processes is a comparator. There are ICs designed for the purpose (called comparators), but where speed is not a consideration, you can even use an opamp. Almost all comparators use an uncommitted collector output, and a pull-up resistor is required. Low values are faster, but consume more current. High value pull-up resistors are uncommon unless speed is not a requirement.
A 'composite' circuit is called a window comparator. The signal must remain within a specified 'window', defined by two amplitudes. The output is high as long as the signal remains within the upper and lower bounds that define the window. It can be broad (several volts between upper and lower bounds) or narrow - just a few millivolts. There are many projects on the ESP website that use comparators, and the ability to detect when a voltage has crossed the preset threshold is used in (literally) countless circuits in common use, both household and industrial. See Comparators, The Unsung Heroes Of Electronics for an in-depth article on the subject.
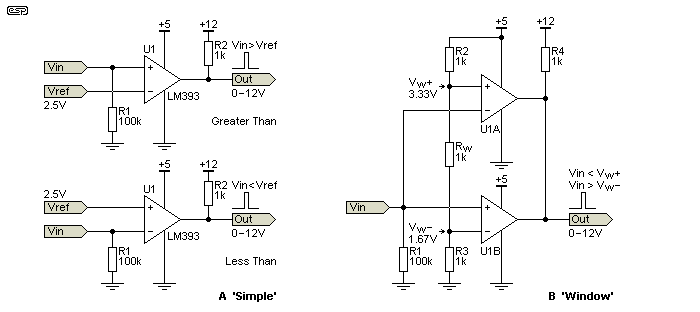
The examples show a 'greater than' and 'less than' comparators and a window comparator. The 'less than' function is achieved simply by swapping the inputs, and a window comparator has both 'greater than' and 'less than' functions. The output of the example shown remains high if the input is within the window (1.67V with the values shown). To change the window, it's simply a matter of increasing or reducing the value of RW. Note that both comparators in B) use the same output pull-up resistor (R4), and the outputs are simply paralleled. If you were to use opamps for the same function, the outputs would need to use isolating diodes, and the output level is less than the main 5V supply voltage (no level shift).
While an opamp can be used as a comparator, the reverse is not true. Comparator ICs almost always have an uncommitted 'open collector' output to allow level shifting, so the circuit can be operated at (say) 5V, but have a 12V (or more) output. Comparators have little or no compensation, and cannot be used with negative feedback. They have propagation delays that are much shorter than any opamp, and are designed specifically for the task of comparing, rather than amplifying.
Digital circuits can also use comparison, and it's a feature built into every programming language ever known. Not every process needs to take a measurement, other than to decide if the input is above or below a threshold. This can happen at any interval that's suitable. For example, a possible water tank overflow (or nearly empty) may only need to be tested each half hour (or longer for a large tank), where a dimmer circuit makes the comparison 100 (or 120) times/ second. A Class-D amplifier will make a comparison at anything up to 500,000 times per second.
Where noise is a problem, comparators are often used with positive feedback, arranged to provide hysteresis (a Schmitt trigger). This improves noise immunity, but it reduces the absolute accuracy of the detection threshold. It can still be made to operate at a precise voltage, but everything has to be taken into account (the reference voltage and output supply voltage). Where a particularly accurate detection voltage is required, it may be easier to make the reference voltage adjustable.
Hysteresis is a property of magnetic materials, where it takes more energy to reverse the magnetic poles than to magnetise them in the first place. It's also used with comparators, primarily to provide noise immunity. Several digital ICs (e.g. 74xx14, 4584) offer hysteresis, most commonly referred to as having Schmitt trigger inputs. A common example of mechanical hysteresis is a toggle switch, where the actuator has to be moved beyond the halfway point before the switch will operate.
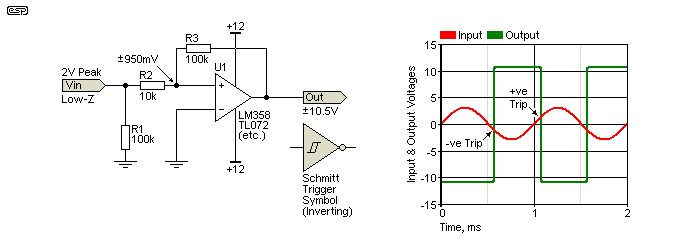
In the example circuit, I've used an opamp, partly to show how they are used as comparators. With 12V supplies, the opamp's output voltage can be ~±10.5V. The voltage divider formed by R3 and R2 provides positive feedback, and has a division of 10, so the input voltage has to be greater than ±1.05V before the output will change state. The reference voltage is zero, as the inverting input is grounded. The input can have up to ±500mV of noise, but the output will still switch cleanly, without 'false triggering' caused by the noise. However, the switching levels are not centred on zero (the reference voltage) because of the hysteresis. This type of circuit is used when noise immunity is more important than absolute accuracy. The amount of hysteresis is determined by the ratio of R2 and R3. Increasing R3 improves accuracy but reduces noise immunity.
Note that with the arrangement shown, the source must be a low impedance. Any resistance/ impedance in series with the input effectively increases the value of R1, increasing hysteresis. This may mean that the circuit doesn't work with your input signal, which would be annoying. The inputs can be reversed (+in grounded via R2) and the signal applied to the inverting input. This reverses the output, so it will go low with a positive input, and high with a negative input. The trigger thresholds are reduced because the output voltage is divided by 11, so it will trigger at ±954mV.
Because an opamp was used, the circuit lacks the precision that can be obtained with a comparator. Even the relatively high slew-rate of a TL072 (13V/µs) means that to traverse the total supply voltage of 24V takes 1.5µs, where an LM393 comparator with a 1k pull-up resistor can swing the voltage in about 180ns (almost ten times as fast!). The LM358 is a low-power and economical opamp choice, but it's painfully slow. Rise and fall times will be around 35µs. Not quite enough time to have lunch while waiting. 
Addition and subtraction are easy, and are as accurate as the resistors used (with a precision opamp). The basic adder is a common sight in audio, but as it's inverting, U3 is used to return to 'normal' polarity. Voltages add mathematically, so if In3 were -2V (for example), the resulting output is 900mV (((3+4)-(-2)) / 10). These circuits are very common in all types of analogue circuitry. Note that all stages are inverting, with the opamp's positive input grounded.

The 'divide by 10' function is included so that input voltages that add up to more than ~13.5V (the maximum available from the opamp) can be processed without error. The basic adder (U1) can have many inputs, and with the values shown you could have up to ten inputs without creating any significant errors. Unused inputs are ideally left 'floating' (not connected), as this keeps noise to the minimum - provided there are no long wires or PCB traces attached. The final outputs of multiple adders may be presented to a log amplifier (for example) so they can be multiplied or divided as needed by the circuit function.
In Fig. 3.1 I've shown a separate inverter to obtain subtraction, but it can all be done with a single opamp. A differential input opamp stage is commonly used to add the signal voltages together, but cancel (via subtraction) any noise voltage present on the signal lines. It can also perform addition/ subtraction as shown next.
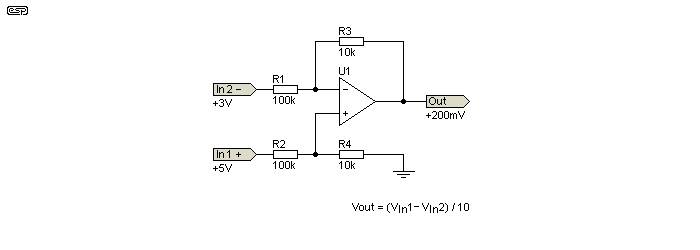
The output is equal to the difference between the voltages at In1 and In2. With the voltages shown, the output is 200mV, because the output is divided by 10. If R3 and R4 are made 100k (or R1, R2 are 10k), there is no division, so the output would be 2V. If both inputs are equal (at any voltage within the opamp's input voltage range) the output is zero. Should the negative input be greater (more positive) than the positive input, the output is negative. Both inputs must be from a low impedance source (ideally less than 100Ω). Opamps can achieve this easily. Any external resistance will cause an error in the output. The circuits in Figs. 2.1 and 2.2 work with AC or DC.
Some readers will be old enough to remember using log/ antilog tables for multiplication and division. These are now a part of history, but for a long time they made calculations a lot easier before we were spoiled by calculators. Even early calculators didn't provide things like square roots, so a 'successive approximation' technique was adopted to solve these. Now, calculators can perform most operations, including complex numbers (aka 'J notation') that are used in electrical (and electronics) engineering. While this is possible with log tables, it's not something I'd recommend to anyone.
The earliest multipliers and dividers were single quadrant, meaning that all inputs and outputs were unipolar (usually positive). 'Quadrants' are covered below. The logarithmic behaviour of diodes or transistors was exploited in these early circuits, with the one shown in Fig. 4.2 being described (albeit briefly) in the National Semiconductor 'Linear Applications' handbook, published in 1980. There are many versions elsewhere on the Net, but many are highly suspect, and some don't work at all. The three caps (all 1nF) were included to make the simulated circuit stable. Without them it will oscillate, and the 'real thing' will be no different.
Logs are easy. Obtaining a logarithmic response from an amplifier only requires a resistor, an opamp and a transistor. However, the function is not particularly linear logarithmic as we expect from a calculator or the like. These work electronically because, with very carefully matched transistors, the function can be reversed (almost) perfectly.
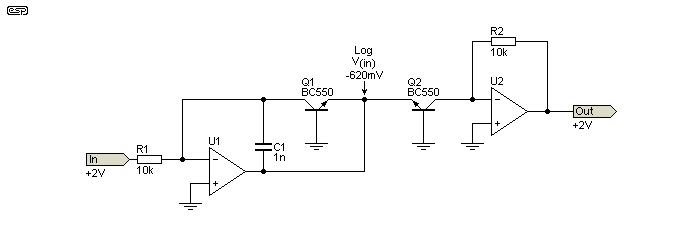
Below 50mV input, the combined output is 'undefined', but above that the functions of the log and antilog amps are complementary, so the output is the same as the input. It looks like you should be able to add a voltage divider or perhaps a series resistor to the emitter of Q2 to get division, and you can. Unfortunately, it's highly non-linear and not useful. The circuit only becomes usable when we add more opamps and transistors.

The circuit shown uses log amps for the three inputs, and an antilog amp for the output. When using logs, multiplication is achieved by adding the logarithms, and division is by subtraction. The answer is the antilog of the added (and/ or subtracted) results. The logarithm base (e.g. Log10, Ln [natural log, base 'e'], etc.) is immaterial - the result is the same. The ability to multiply and divide numbers is essential for any analogue computing system. These were used for ballistics calculations (e.g. military applications) and other processes before digital computing existed. It's probable that similar circuitry is still used in some systems, because it's comparatively low-cost, and can be very fast. However, like the Fig. 4.1 circuit, it doesn't work properly if any input is below ~60mV. However, if all inputs have the same voltage (not particularly useful) it will function down to about 10mV on all three inputs.
The transfer function of the complete Fig. 4.1 circuit is ...
Vout = ( Vin1 × Vin2 / Vin3 ) / 10
The log and antilog amps are neither 'natural' logs (base 'e') nor log10. The base is determined by the transistors, which are used as 'enhanced' diodes. While it is possible to use diodes, the dynamic range is severely restricted. In the above, and as simulated, if In1 is 5V, In2 is 3V and In3 is 1V, the output is 1.4937V (it should be 1.5V). Note that In3 must be 1V for simple multiplication, because if In3 were (for example) 0V, that would create a 'divide by zero' error, and the output will try to be infinite. It can't exceed the supply rail of course.
If In3 were made 0.5V, the output still follows the formula almost perfectly, giving an output of 2.967V (it should be 3, an error of 1.1%). To use a value we're all familiar with, if In1 and In2 are 1.414V (In3 at 1V), the output is 200mV (1.414² is 2, as 1.414 is the square root of 2 - √2). By applying the same signal to In1 and In2 with In3 at 1V, the circuit generates the square of the input. 2V input will result in 400mV output (4V/10). It's easy to see why the divide by 10 is included, because squaring any voltage over 3.87V would cause the output to (try to) exceed the opamp supply rails.
Log/ antilog circuits can use diodes, but they have a limited dynamic range and one of the things included above can't be incorporated - division. There are many examples, but not all simulate properly, some not at all. You need to select this type of circuit carefully if you wish to analyse them. They are not intuitive, and they all have limitations.
A basic understanding of logarithms is essential in electronics, especially where sound and light are involved. Human senses are logarithmic, as that's essential for us to be able to (for example) hear very quiet sounds, and not be completely overwhelmed by loud sounds. Our hearing has a range from 0dB SPL to around 130dB SPL, a range of about 3.16 million to one. Our other senses are also logarithmic (light, touch, etc.), and this is a huge evolutionary benefit. It allows us to experience an awesome range of sensations without 'overload'. The decibel is the best known of these log progressions, and we encounter it every time we work with audio electronics.
Pitch perception (musical notes) is also a log function, with the Western 'equally tempered scale' being based on the 12th root of 2 (an octave is double or half the starting frequency). An octave is covered by 12 semitones. There are several (many) other scales that follow different rules, but the equally tempered scale (aka 'equal temperament') is one of the best known and widely used for 'Western' music. There's lots of info available that won't be repeated here, nor do I intend to discuss the 'just' scale (which is similar, more 'tuneful', but irrelevant here).
Analogue multipliers are often described by the quadrants they can handle. The simplest is a single quadrant, where all inputs and outputs are a single polarity. A two-quadrant multiplier allows for one input to be of one polarity only, with the other able to be either positive or negative. The output is also bipolar. The most useful are four-quadrant types, where both inputs and the output can be positive or negative.
The convention is that the inputs are designated 'X' and 'Y', and they can be single-ended or (more commonly with ICs) differential. The output is almost always scaled (generally reduced by ×10) so that the output doesn't saturate with high input voltages. Most also provide for an output DC offset. One of the earliest analogue multiplier ICs was the MC1495, a wide band four-quadrant type. The inputs had to be manually trimmed to minimise DC offsets, and the output scale factor could be changed from the default. I first came across these in the mid 1970s, as they were used in the original version of the Electronics World 'Frequency Shifter For 'Howl' Suppression', designed by M. Hartley Jones (see Project 204 for an updated version).
The datasheet for these ICs is very comprehensive, and shows the things it can be made to do. Of these, obtaining the square root remains a problem, but it's not insoluble. Squaring (which includes frequency doubling for AC inputs) is easy. There used to be quite a few analogue multiplier ICs, but the number has shrunk. Today, the AD633 is a 'low cost' version, and the AD834 is a high-speed version (and very expensive). The TI MPY634 is another (also expensive) but it includes some extra circuitry to allow square roots without an external opamp.
| Type | Vx | Vy | Vo |
| Single Quadrant | Unipolar | Unipolar | Unipolar |
| Two Quadrant | Bipolar / Unipolar | Unipolar / Bipolar | Bipolar |
| Four Quadrant | Bipolar | Bipolar | Bipolar |
'Simple' circuits like that shown in Fig. 4.1 are single-quadrant. All inputs to that circuit are positive, as is the output. While this works for basic calculations, it's very limiting for many other tasks that use multiplier circuits. As shown above, multiplication is easy, but division is somewhat less so. Many of the early circuits used logs and antilogs to compute the result. They require very carefully matched (and thermally coupled) transistors, but can use surprisingly 'pedestrian' opamps. Most of the simulations I did used TL072 opamps, and the results are 'satisfactory'. Unlike a calculator where the result is accurate to perhaps 10 decimal places, they are rather wildly inaccurate by comparison (but generally within 2% or so).
It could be argued that an opamp gain stage is a multiplier, since the input voltage is multiplied by the gain. However, this is inflexible, as one operand remains fixed. It can be made adjustable with a pot or switched resistors, but it's still recognised as a gain stage, not a multiplier. The same applies to voltage dividers or transformers. A true multiplier does what it sounds like - it multiplies two (or more) values together. The input(s) can be voltage or current, depending on the source transducer and what you are trying to achieve.
Four-quadrant multipliers have been available as ICs since the early 1970s, with the MC1496 balanced modulator/ demodulator and MC1495 wide band four quadrant analogue multiplier being good examples. The original purposes were mainly radio frequency, for tasks such as amplitude modulation and synchronous detection. The original datasheets made no reference to audio frequency applications, but it didn't take long before people discovered that they worked just as well at audio frequencies as RF.
The basis of (almost) all multipliers is the Gilbert Cell, using cross-coupled long-tailed pairs with a variable 'tail' current used to change the gain. Barrie Gilbert is said to have based his invention on an earlier design by Howard Jones (1964) - see Wikipedia for all the details. A greatly simplified version is used in Project 213, a DIY voltage controlled amplifier that uses a 2-quadrant multiplier. It could be argued that it's really a 1½-quadrant, because both of the inputs have to be positive, but the output is bipolar.
The following drawing shows an MC1496 multiplier, configured as a 'typical' modulator. Although RF operation is assumed, the 'carrier' signal can be audio, and either a variable DC voltage or a low-frequency sinewave can be used for modulation. These will provide gain control or amplitude modulation (tremolo) respectively. Predictably, when either input is at zero volts, the output is also zero (any number multiplied by zero gives a zero result).
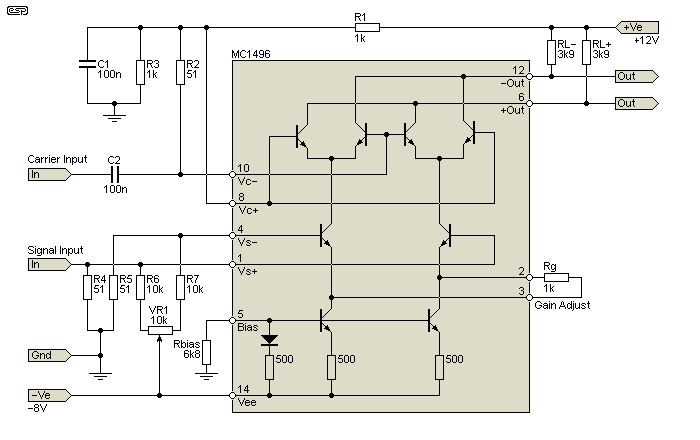
The 51Ω resistors are intended for RF usage (50Ω is a common RF impedance), and can simply be increased to something more suited to audio. Around 10k will work just fine. Because of the way it works, the audio would be applied to the 'signal' input, and C1/ C2 would have to be increased to around 10µF to provide a low impedance. The modulating frequency might be a 2-15Hz sinewave applied to the 'carrier' input to obtain tremolo for a guitar or other instrument. The modulation input also requires a DC bias, otherwise there would be no audio without the modulation. If it were to be biased to 1V, the audio output without modulation will be the same as the input level. The modulation can be a maximum of ±1V with respect to a modulation input bias of 1V.
Note that the circuit shown operates as an amplitude modulator with suppressed carrier (radio buffs will understand this). With 1 1MHz carrier and 1kHz modulation, the output contains the upper and lower sidebands at 999kHz and 1,001kHz, but the 1MHz carrier is not included (it's suppressed - hence the term). 'Traditional' amplitude modulation can be obtained by swapping the carrier and modulation inputs. A complete description is outside the scope of this article, but I encourage you to research this further if you think it's interesting. I think it is, but my interests extend well beyond audio.
The MC1496 is a four-quadrant multiplier, but the MC1495 would normally be the device of choice. I used the 1496 because its datasheet has the (simplified) internal schematic. This isn't provided for the 1495. These ICs have been obsolete for many years, and the modern equivalent is the AD633. This is a much better IC, and it's laser trimmed during production to minimise problems with DC offsets and to ensure it meets accuracy specifications.
As noted above, Project 204 (frequency shifter) uses a pair of AD633 multipliers, which improved the performance and ease of setup over the original using MC1495 multipliers. While the AD633 is listed as 'low cost', that's a matter of opinion. Personally, I don't consider an AU$30 IC to be 'low cost', but it is true compared to others costing over $100. For the purposes of explanation, the multiplier used in following drawings is 'ideal' (created as a non-linear function in the simulator). The transfer equation is (mostly) unchanged. The exception is Fig. 6.2, which is a reproduction of the Project 213 VCA.
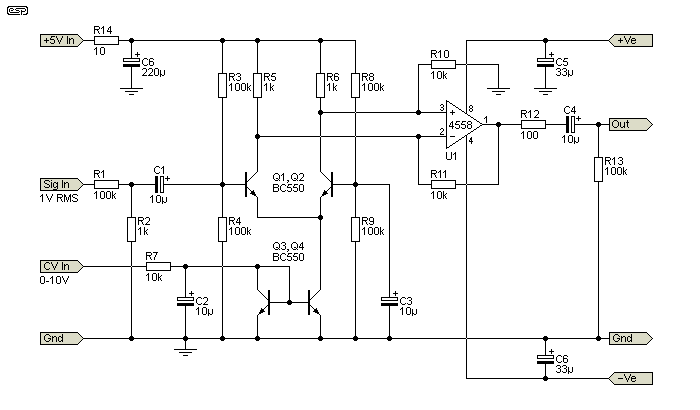
The circuit is a bit of an odd-ball, because it doesn't really fit into the definitions of quadrants. Had the current sink (Q3, Q4) been referred to the negative supply, that would allow it to handle a bipolar input signal, but the control signal remains unipolar. By that definition, it's a 2-quadrant multiplier. I didn't design it like that because it doesn't work as well as the version I published (yes, I tested it), and it has the advantage of a control signal that's ground referenced.
Four quadrant multiplier ICs can be used for multiplication, division, squaring and square roots. Division and square roots require an external opamp. The square root circuit is still tricky, because a diode is needed to prevent latch-up that can occur if the input is zero or negative (even by a couple of millivolts). You can't take the square root of a negative number (or zero). Very careful offset control (or an ultra-low offset opamp) is required, or the circuit below can't take the root of any value less than 3mV (the answer is 54.77mV). Whether this is a problem or not depends on the application. It is limiting though, unless the input signal remains above the lower limit at all times.
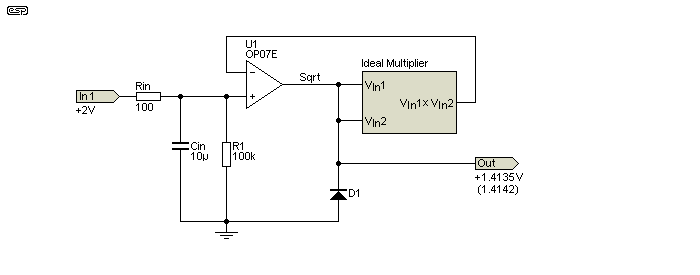
The multiplier uses almost the same formula as shown above (Vout = Vin1 × Vin2 / 10), but the final divide by 10 is omitted. The diode prevents issues with zero or negative inputs. If an offset is applied (which must be temperature compensated), it's (theoretically) possible to take the square root of 1mV (which is 31.6mV), but expect a significant error at such a low input! The result will be reasonably accurate when the input is greater than 100mV (√100m = 316.2m).
The square root extractor is still capable of working accurately with less than 100mV input, and the lower limit of the circuit shown (as simulated) is 50mV (peak or DC) for passable accuracy. Using a Schottky diode for D1 may help, and the circuit can theoretically measure down to less than 50mV input (√50m = 223m), and it's acceptably accurate down to that level. There doesn't appear to be a sensible way to improve the performance beyond that lower limit. With some messing around, I was able to simulate a square root of 5mV (70.7mV) and get a result of 70.9mV. With this kind of circuit, there's a continual fight between man (me) and machine (the simulator software). Simulators often need to be 'tricked' into doing what they're told. The 'trick' in this case was to include Rin and Cin. These prevented any momentary excursion into negative territory which causes the circuit to latch-up. Zero and negative values are 'illegal' states for a square root extractor.
Bear in mind that these results are simulated, and use an ideal (zero error) multiplier. Should you build one using real parts, expect to be disappointed. You also need to know your simulator pretty well, and know how to trick it into doing things it normally won't do. Square roots are as irksome in hardware as they are anywhere else.
They have been the bane of maths teachers' lives since ... forever. Some of the important properties of square roots are listed on line at a number of sites [ 4 ], and I don't propose to go into detail here. I do suggest that you do a web search though - if for no other reason than to see the different approaches and to understand that a square root is (or was) a pain in the bum!
If you think that obtaining the square root of a number looks complex, it is. If you look up 'square root algorithm' in a search engine, the number of pages is impressive, and the methods vary from being complex to very complex. With calculators and computers we tend not to give it a second thought, but the process is quite involved. Irrational numbers can take considerable computing power, regardless of the method used. One technique that seems to be missing almost everywhere is ...
Sqrt X = X ^ (1/2) For example (and simplified) ...
√123 = 123 ^ 0.5 = 11.09053651
Alternatively, you could use (base 10) logarithms ...
√123 = 10 ^ (log(123) / 2) = 11.09053651
... and get the same answer.
I know which one is the simplest.  It's also easy to remember without having to perform too many mental gyrations. Raising to a power is supported in most major computer programming languages, and it's (probably) fairly efficient, especially when compared to the 'successive approximation' technique. If you had to rely on 'standard' 4-figure log tables (assuming that anyone still knows how to use them), the result is 11.0904. Not exact, but close enough (when squared you get 122.9969). Almost no-one would bother with log tables any more, as most calculators have the √ function and exponentiation (raising to a power). They're even on my phone!
It's also easy to remember without having to perform too many mental gyrations. Raising to a power is supported in most major computer programming languages, and it's (probably) fairly efficient, especially when compared to the 'successive approximation' technique. If you had to rely on 'standard' 4-figure log tables (assuming that anyone still knows how to use them), the result is 11.0904. Not exact, but close enough (when squared you get 122.9969). Almost no-one would bother with log tables any more, as most calculators have the √ function and exponentiation (raising to a power). They're even on my phone!
Any waveform that is not an almost 'perfect' sinewave will be subjected to potentially large errors if it isn't measured using 'true RMS'. Most low-cost meters use average-responding, RMS calibrated measurements, but the measurement is only accurate if the input is a sinewave. For example, a 1V peak (2V p-p) squarewave will be displayed as its average, RMS calibrated, which is 1.11V - 11% high. With a true RMS meter, it will show as 1V as it should. Some waveforms are much worse, with errors that can exceed -50% (more than 50% low).
With an RMS converter, the input signal must be squared, and not just full-wave rectified. The average of the latter is 0.6366 of the peak value, whereas the average of the signal squared is 0.5 of the peak. Squaring can follow rectification, but the rectifier is not necessary because the value of -x² is the same as x². The process of squaring includes rectification by default.
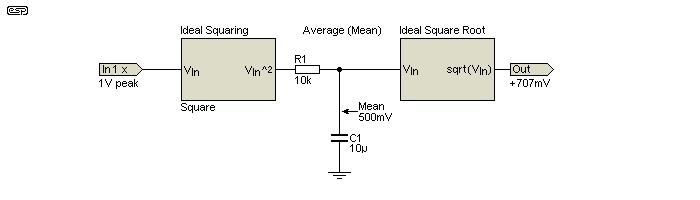
Since we don't have access to 'ideal' squaring and square root blocks outside of a simulator, we need to be more adventurous. While the circuit shown next still shows ideal multipliers, AD633 ICs will actually work fairly well, provided we're careful to minimise DC offsets. The method shown in Fig. 8.1 is (in the simulator) almost perfect - the result is virtually identical to the measurement taken with the simulator's maths functions that are used to measure the RMS value (amongst other useful things).
Multipliers can be used to convert a waveform to 'true RMS'. RMS stands for 'root mean squared', and is required with any waveform that's not a sinewave to prevent inaccurate readings. The limitation is the square root circuit, which as noted above is less than perfect. The concept is simple in theory - square the input voltage, take the average, and take the square root. For example, a 1V peak sinewave is squared, which provides a signal at twice the input frequency, but unidirectional (the square of a negative value is positive). The average taken at the positive end of C1 is 500mV. If we take the square root of 500mV we get 707mV (close enough), which is the RMS value of a 1V peak sinewave. This works with any waveform, and gives the true RMS voltage.
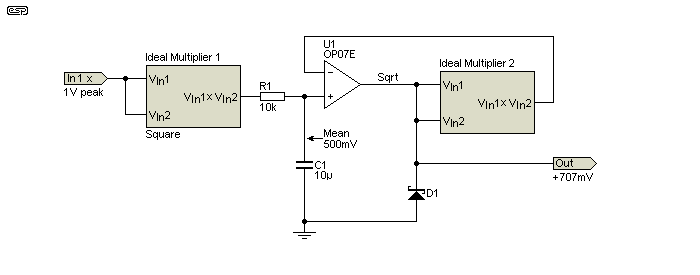
The circuit is conceptual, in that if multiplier ICs are used they must be configured to have unity gain (multiplier 2 in particular) rather than the default divide by 10. As shown, I used the SIMetrix 'Non-Linear Function', configured as an arbitrary source with the formula shown in the boxes. Both are configured to square the input. The output is accurate between 100mV and 2V (peak) input, but at lower voltages the accuracy gets progressively worse as the input voltage is reduced. A 100mV AC input has a mean value (after squaring) of only 5mV. The square root of 5m is 70.7m (70.7mV) but the output is 70.9mV (which is actually pretty good). It gets worse at lower inputs. The opamp must be a precision (ultra-low offset) type (I used an OP07E in the simulation).
Performance is fairly poor compared to an IC such as the AD737. These are described in some detail in AN-012, Peak, RMS And Averaging Circuits. These use a somewhat different principle to obtain the RMS value, that works down to low levels without losing accuracy (measurement speed and bandwidth are still limited at low input voltages though). An improved version is the AD536, but that comes at a cost (over AU$100 from the suppliers I checked). In some respects, this is all academic when compared to digital sampling measurement systems, where the RMS value can be determined (using digital calculations) almost instantly.
However, if the signal is varying, a digital readout is of no use to man or beast, and an analogue meter movement is a far better option. You need to be sure that you need something like this though, as the cost is significant (especially when you add a power supply, preamp, range switching, etc.). Mostly, we all just use a digital multimeter (preferably true RMS if you need accuracy). If a signal is varying over a fairly wide range (e.g. music) we can only estimate the voltage, and accuracy isn't possible whether we measure true RMS or average.
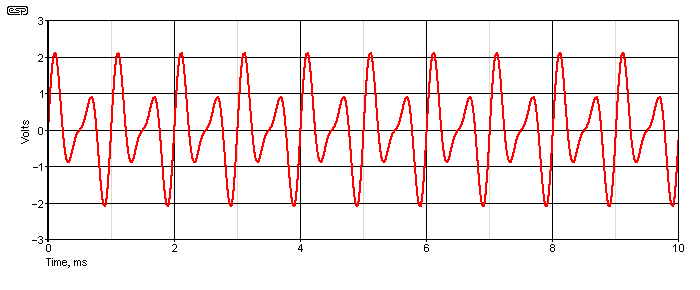
The waveform above consists of 1 'unit' at 1kHz, 4 units at 2kHz and 2 units at 3kHz (each unit is 333mV peak). The RMS value is 1.08V, but if it's full-wave rectified and the average (mean) taken (RMS calibrated), you'll get a reading of 957mV, an error of -11.4%. The two 'concept' circuits get the right answer, regardless of the apparent 'complexity' of the waveform. When a meter reads average but is calibrated as RMS (very common in cheap meters), any non-sinusoidal waveform will cause problems. With a sinewave, true RMS and average (RMS calibrated) meters give the same reading.
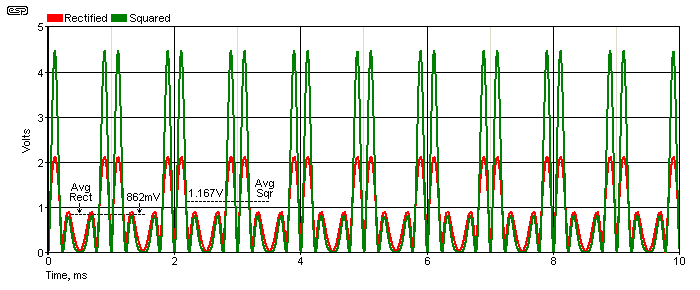
To display RMS (sinewave) with an averaged input, the rectified and averaged input signal needs a gain of 1.111. The sinewave, after the process of full-wave rectification (as opposed to squaring), gives a 636.62mV average output for a 1V peak sinewave, and if that's amplified by a factor of 1.111, the answer is 707mV, which is correct. It only works with a sinewave - other waveforms give wrong answers. Fig. 8.4 shows the difference between rectification and squaring, using the Fig. 8.3 waveform. The rectified average is 843mV, and squaring gives 1.667V.
The square root of 1.1667V is 1.08V (which is correct), but the rectified average is only 862mV, and after amplifying by 1.111 to get 'RMS' equivalent, the output is 957mV, which is clearly wrong. Unfortunately, these calculations are difficult, and the simplest proof is to use simulation.
A power measurement with DC is easy. Multiply the voltage and current, and voila! 12V at 1A is 12 watts, and there is no ambiguity whatsoever. With AC, it's very different, because the product of voltage and current is VA (volt-amps), and it may or may not be the same as the power. If the load is resistive (a resistor or heating element for example), then VA and watts are the same, but if the load is inductive, capacitive or non-linear, the two are usually very different.
A 'well behaved' reactive load (one with capacitance and/ or inductance) may show that the voltage and current measured gives (say) 100VA, with the power being 80W. The only way you can measure that is with a multiplier. It can be analogue or digital, but it must be able to distinguish the phase angle between the voltage and current. With a resistor, there is no phase angle - current and voltage are perfectly in phase. The 'power factor' of a load that draws 100VA and 80W is 0.8 (unity is ideal).
A 'proper' wattmeter was described in Project 189, an audio wattmeter that shows the real power delivered to a loudspeaker. Both the amplifier and the loudspeaker have to contend with the voltage and current, even when they don't contribute any energy to the motor structure(s). But you can't just measure these two quantities and call it 'power', because it probably isn't. This is a topic that I've covered in some detail in the discussions about power factor (see the Lamps and Energy section on the ESP site).
An analogue multiplier is a simple way to determine the real power. It still uses the voltage and current, but works with any phase displacement between voltage and current or a non-linear load, and provides the power, not VA. The electricity meter at your house only measures power, and that's what you pay for. In the circuit shown next, the output level is 1mV/W, but that's easily changed by adding gain (using one or two opamps). I've used an 'ideal' multiplier, but if you build the circuit with an AD633 it will perform perfectly. I know this because I've done so, and it's a great testing tool.

For the 'real thing' please see the project linked above. This is not a toy, it's a genuine wattmeter that indicates watts, not VA. The circuit above has an inductive load that draws 3.113A at 50V RMS. That's 155.5 VA (voltage multiplied by current), but the wattmeter shows that the power is 97W. The current transformer (CT) converts current to voltage, with a transfer ratio of 100mV/A. R3 is known as the 'burden' resistance, and it's always a low value to prevent core saturation in the CT. R1 and R2 form a 100:1 voltage divider, as a 'real' multiplier IC cannot handle an input of 100V RMS.
The output of the circuit will always show true power, regardless of the frequency, voltage, current, phase angle (between voltage and current) or waveform distortion. In a realistic circuit as described in the project page, there are upper and lower limits to all inputs. The current transformer can't handle frequencies much below ~40Hz (depending on its characteristics), and the multiplier has an upper frequency limit. For the AD633, that's quoted as 1MHz. The accuracy should be better than 5% overall, but it can be adjusted to be more accurate. The display would typically be an analogue meter movement if you're monitoring audio.
VA is often referred to as 'apparent power', versus 'true power' (in watts). A reactive load returns some of the current drawn back to the source, be it the household mains or an amplifier. This happens because the voltage and current are not in phase. Non-linear loads (such as a power supply - an example is shown to the left of the wattmeter) don't return anything to the source, but they usually have a poor power factor because the load current is distorted. In this case, the load draws 3.954A, giving 197VA and power of 161W. Without a wattmeter, you cannot determine the power without many tedious calculations.
Of course, you can just buy a digital wattmeter for mains measurements (these generally include the current transformer), and the calculations are performed digitally. See Project 172. These certainly work (I have several), but they aren't as much fun, and of course they don't teach you how the power is determined. They are useful though - that much is undeniable. Don't expect to use one to measure audio though, as the sampling rate is almost certainly far too low to handle anything above ~100Hz with any accuracy.
The final systems I'll look at here are integration and differentiation. These are common mathematical functions, that are used to extract an 'interesting' characteristic of a signal. They are also very common in mathematical equations. They are used in calculus, and are (or can be) complementary functions. Differentiation is used to determine the rate of change of a signal, while integration is used to work out the 'area under the curve' - how much charge is experienced over time. This article is not the place for detailed explanations of the mathematical functions, which include algebraic, exponential, logarithmic and trigonometric. Everything you wanted to know can be found on websites that concentrate on mathematical processes - there are many of them, and a search will find a wide range.
In electronics, integration and differentiation are quite common. For example, a differentiator provides the rate-of-change information of a signal, and an integrator provides amplitude and duration info, which may be cumulative. Both are achieved with opamps for precision applications. In the simplest of terms, an active differentiator is a high-pass filter, and an active integrator is a low-pass filter, but they are both more 'radical' than conventional filters. 'Active' implies the use of a gain stage, which is usually an opamp. Both are shown in Fig. 10.1.
The frequency is easily calculated using the standard formula (f=1/(2π×R×C), and is 15.9Hz for both circuits (R1=R3=100k, C1=C2=100nF). The integrator has a second defined frequency, set by R2 and C1, and it stops integrating at 1.59Hz. When wired in series, the output is flat down to 1.59Hz (the -3dB frequency). R2 is an unfortunate necessity, as without it the opamp has no DC feedback. With no input, the output will slowly drift to one or the other supply rail.
Integrators and differentiators don't have to use an opamp - a simple RC (resistor/ capacitor) network works, but it's not linear. The charge and discharge curves are exponential because the voltage across the resistor changes. The 'time constant' of an RC network is R×C, at which point the capacitor's voltage has risen (or fallen) by 63.2%. If 10V is applied to a 100nF cap via a 100k resistor (TC=10ms) the voltage will reach 6.32V in 10ms. When the same cap is discharged from 10V via a 100k resistor, its voltage will be 3.68V after one time constant (10ms). The -3dB frequency is calculated from the time constant too (f=1/2πRC). The term 'RC' is the time constant.
Passive integrators and differentiators are commonly used as simple filters, with a slope of 6dB/octave. Even the common coupling capacitor (in conjunction with an amplifier's input impedance) is a basic differentiator if the applied frequency is low enough. The -3dB frequency is calculated from the formula f = 1/2πRC. For most audio circuits, this will be below 20Hz, and often below 2Hz to ensure minimal rolloff at the lowest frequency of interest. We don't think of it as a differentiator, but it is.
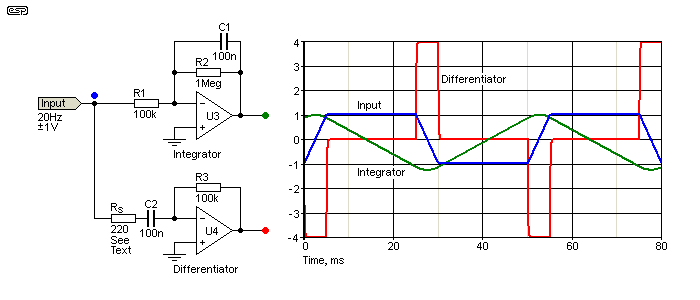
Both circuits are normally inverting and they are controlled by the input current, which is supplied to the inverting input (a virtual earth/ ground). The differentiator uses the instantaneous current through the input capacitor to provide an output that's directly proportional to the peak amplitude and rate-of-change, and the output of the integrator is proportional to the amplitude and duration of the signal. The signal current causes the integrator capacitor to charge, and both the amplitude and duration determine the output voltage. If the two circuits are wired in series, the output is (almost) an identical copy of the input. The difference is due to R2 (1MΩ). Rs in the differentiator is included to prevent 'infinite' gain at high frequencies. High frequency response is limited to 7.23kHz with 220Ω as shown.
The input signal was deliberately slow so the transitions are visible. Rise and fall times are 5ms, which I selected so that calculations are within the voltage range that opamps can handle. The integrator uses a 100nF integration cap, and R2 is included so the opamp has DC feedback. This limits the low-frequency response of the circuit. While the signal is at its positive or negative maximum, the input current is limited by R1, and is ±10µA. The output of U1 is the integral of the input current, and the voltage increases/ decreases at a rate of 100V/s (100mV/ms). During the period of one cycle (50ms), the integrator's output swings from +1.1V to -1.1V. Because the rise and fall times are 5ms, the integrator provides a voltage that is proportional to the voltage above or below zero, and accounts for the rise and fall times. The maximum rate-of-change for the integrator is 10V/s with 100nF and 100k.
By their nature, integrators force a constant current through the capacitor, with the current determined by the input resistance and applied voltage. If a 1V DC signal is applied to the input of the integrator, its output will rise/fall at a rate of 100mV/ms, exactly as predicted. It's not normal procedure to apply a steady input voltage or a repetitive waveform to the input of an integrator, as they are intended to be used to determine (and perhaps correct) long-term error voltages. Integrators are used to remove DC offset from critical systems, and they are also used as a 'DC servo' for audio power amplifiers to (all but) eliminate any offset. The use of a servo can ensure an amplifier has less than 1mV of DC offset (see DC Servos - Tips, Traps & Applications for a full description).
An integrator creates a constant current across the capacitor so it charges linearly, as opposed to the exponential curve seen when a cap is charged via a resistor. The current is determined by the input voltage and the value of the input resistor. The voltage across a capacitor can easily be calculated for any capacitance and constant input current. A 1F capacitor will charge by 1V/s with an input current of 1A. This is easily extrapolated to more sensible values, so a 1µF cap will charge by 1V/s with a 1µA input current, 10V/s with 10µA, etc. The formula is simply ...
ΔV = I / C For the example shown in Fig. 10.1 ... ΔV = 10µA / 100nF = 100V/s (100mV/ms or 100µV/µs)
During a transition of the 20Hz waveform, the input current to the differentiator is ±40µA, through C2. As the rise/ fall time is 5ms and the capacitance is 100nF, the effective impedance of C2 is 50k (5ms/100nF), so the charge current is 40µA. The formula shown below is preferable to calculating the effective impedance, although both methods work. The voltage across R3 is I×R (40µA×100k=4V). If the rise/fall times were reduced to 1ms, the charge current is increased to 200µA, with an output voltage of ±20V. That's greater than the supply voltage, and the value of R3 must be reduced. In a real circuit, RS is almost always needed so the opamp doesn't have extremely high gain at high frequencies. The value will be between 100Ω and 560Ω in a typical circuit. I used 220Ω, which has a negligible effect at the impedances used. The capacitor current is determined by the voltage change and rate-of-change (2V and 5ms respectively) ...
I(C) = C × ΔV / Δt (Where Δ means change) For example ... I(C) = 100n × 2 / 5m = 40µA
The output voltage is then determined by the value of the feedback resistor ...
VOut = I(C) × Rf so ... VOut = 40µ × 100k = 4V
In some cases, integrators are set up with an automatic discharge circuit that resets the voltage to zero when it reaches a preset limit. This forms a very basic analogue to digital converter, where the output frequency is determined by the input voltage (a voltage-frequency converter). This is known as a 'single-slope ADC', which is enhanced to become a 'dual-slope ADC' - these were the basis of most digital multimeters, and are still used. The dual-slope ADC has the advantage that component tolerance is balanced out, and it's therefore more accurate. The number of pulses counted tells you the average input voltage over time, and measurements can be taken over a period of months or even years. The output frequency is directly proportional to the input voltage. The rate-of-change of the cap voltage is determined by V = I / C, so with 2µA and 100nF, the rate-of-change is 20V/s. That means it takes 200ms to reach the reset trip voltage of 4V.
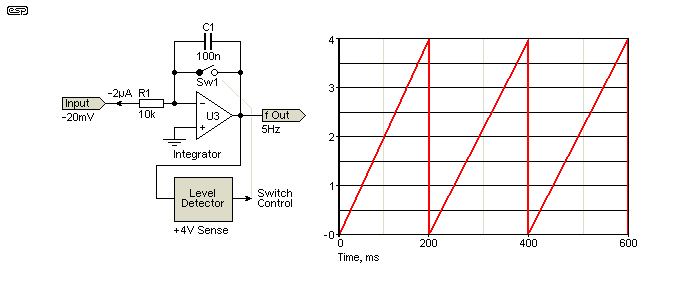
The output frequency is 5Hz for a -20mV input, and if the input is increased to -40mV, the frequency is 10Hz (the input voltage must be negative for a positive output because the integrator is inverting). It can be scaled to anything you like, provided it's within the frequency range of the opamp. Scaling is done by increasing or reducing either R1 or C1. The level detector is set for 4V, and when the voltage reaches that, the cap is discharged and the cycle repeats. The switch will most commonly be a JFET, but it can be anything that has low leakage and a low 'on' resistance.
A circuit such as this can be very accurate, but a low-leakage capacitor is a must for long cycle times. I first saw this arrangement used for long-term temperature monitoring at a water storage dam near Sydney, in ca. 1975. For its time, it was a work of art. It should be accurate to within 1% over at least five decades, with the discharge time being the dominant error source. The detector's reference voltage must also be stable, and a high-stability capacitor is essential. PCB leakage is a potential error source with very low input current, and Teflon (PTFE) stand-off terminals may be needed if low input current is provided by the sensor. The opamp must have very low input offset and negligible input current.
As noted above, dual-slope ADCs are common (and still readily available in IC form). I don't propose going into more detail here as it's not really relevant to the general topic, but as always there's a lot of info on-line, including manufacturer datasheets and detailed descriptions. Most new ADCs are ΔΣ (delta-sigma), and integrating ADCs are becoming less popular.
A common application for integrators and differentiators is a 'PID' controller [ 5 ], which uses proportional control (a simple gain stage), the integral (from an integrator) and derivative (from a differentiator) to reach the target value as quickly as possible. These are discussed in some detail in the article Hobby Servos, ESCs And Tachometers (which goes beyond 'typical' hobby circuits).
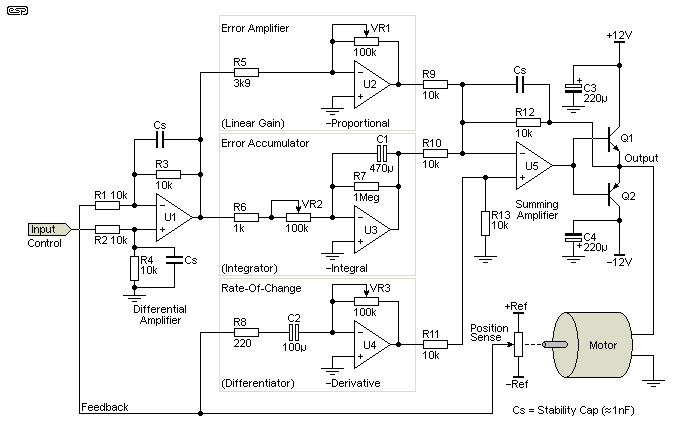
A PID controller is shown above, and while it includes a motor, it can just as easily be a heater, cooling system, or any other process that requires rapid and stable servo performance. One common usage is 'high end' car cruise-control systems, where very good control is necessary to prevent over-speed (in particular). The proportional section (top) is the primary error amplifier, and it does most of the 'heavy lifting'. Many simple servo systems use nothing else. The differentiator (derivative) applies a voltage that's proportional to the rate-of-change of the feedback signal, and it's used to (briefly) counteract the main proportional control to minimise overshoot. The integrator accumulates and removes long-term errors. These controllers are 'state-of-the-art', although many modern ones are digital (or digitally controlled).
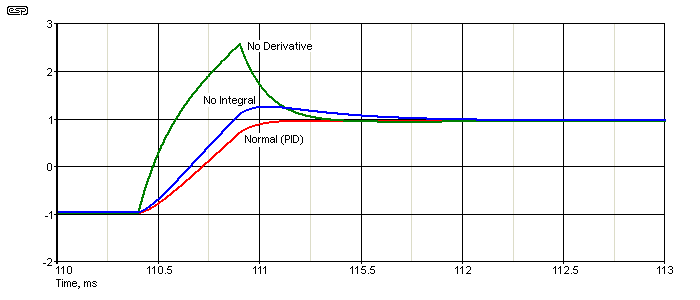
The graphs show what happens when the system is operating as intended (red), without differentiation (green) and without integration (blue). With the differentiator disabled, there is a large overshoot, and a smaller overshoot when only the integrator is disabled. The 'normal' graph shows almost perfect response. The load was simulated to have mass (inductance), inertia (capacitance) and friction (resistance). The signal rise time was set for 500ms, a 'sensible' limit for the simulation. Real life means real values of mass, inertia and friction, and the PID controller's trimpots are used to obtain the optimum settings. The damping effect of the derivative is particularly pronounced.
If the controlled element is not a servo as shown in Fig. 10.3, the sensor will be different from the 'position' pot shown. It can be a tachometer (to control a motor's speed), a thermistor (to control temperature) or a light sensor to enable 'daylight harvesting' for lighting systems. These are fairly new, and they are set up to dim (or turn off) internal lighting when there's sufficient daylight to allow the lamps to be operated at lower power. The energy (and cost) savings for a large warehouse (for example) can be significant. All of these functions are used in modern manufacturing systems.
This is as far as I'm taking the process here, but there are many engineering sites that go into a great deal of detail on the setup and use of PID controllers. The main points to take away from this relate to differentiation and integration. These functions are widely used, often without you realising that they are there. These 'simple' analogue circuits are truly ubiquitous - they are (literally) in so many systems that attempting to list them would be futile.
There's probably a lot here for you to get your head around, so it's best taken a step at a time. True RMS voltage readings aren't easy to grasp at first, and power (vs. VA) is something that causes many people problems. When you have phase shift or distorted waveforms, simple calculations don't work. However, even comparatively simple analogue multiplier (or RMS converter) IC circuits can solve these easily. Understanding how they work isn't essential to be able to use them, but it does fill in the gaps. Understanding the processes helps you improve your overall knowledge - never a bad thing.
None of the material here suggests that analogue techniques are no longer useful. Sometimes, analogue from input to output gives a better (human readable) output. One major problem with analogue computers is that they must be specifically configured for a particular calculation. This is limiting for 'general purpose' applications, but if there is a specific problem to be addressed (and cost isn't an issue), the analogue approach can still be a good solution. It has the advantage of speed, as there is no analogue to digital conversion (nor the inverse), and may be ideal where reconfiguration is never needed. All systems have limitations, and while modern computers are so powerful (and take up so little space), that doesn't mean that their limits cannot be exceeded (application dependent of course). They are also more of a 'one-size-fits-all' approach, as the system is configured in software, and not hard-wired.
However, once an analogue system is wired to do what you need, it can't be messed up by a software update, and it should perform as designed for many years. Thermal drift is a potential problem of course, and this may also affect the sensors used (that's an issue with analogue and digital systems). Should you decide to build a dedicated analogue computer, you will have many challenges. This applies if you elect to use a digital system as well, and while the latter can be reconfigured with software, the testing needed to ensure that it never runs off 'into the weeds' can be very time-consuming.
Many of the circuits described here are no longer in common usage, but they remain interesting and provide a background to the development of circuitry as we now know it. The 'old' ways of doing things haven't gone away though - they are just hiding. Most people will never get to play with an analogue multiplier, at least not called by that name. Voltage controlled amplifiers (VCAs) owe their very existence to multipliers, because that's what they are. Most true RMS multimeters use a dedicated RMS converter IC, even those that are microcontroller based. The micro generally only controls the display - it doesn't have the power or processing speed to perform irksome maths functions.
Some things remain difficult with analogue processes (e.g. square roots), and there's not much you can do to change that. As noted above, these are even difficult with a digital system that doesn't have an appropriate algorithm built-in, because they are troublesome, and have been since ancient times. Analogue hardware can only do so much before the whole system is tipped into instability or even lock-up. As always, if there's an alternative to a complex problem, use it.
Most of the functions that used to be done with multipliers (calculating RMS for example) are now performed with ICs dedicated to the purpose (ASICs), such as the AD737 (described as a 'low cost, low power, true RMS-to-DC converter'). Like the 'low cost' multipliers, the term is subjective, as they're not cheap. However, a single IC does almost everything. Simply apply AC to the input, and extract the true RMS value as a DC output. The hardware is specifically designed to avoid troublesome circuitry.
Please be aware that your simulator package may or may not run with all of the ideas posted here. Some will be no problem, while others just won't work. They do work with SIMetrix (with trickery in a few cases), but I haven't tested any of these circuits in any other simulator. I normally avoid circuits and simulations that can't be reproduced by anyone, anywhere, but these are 'special' cases. It's unlikely that anyone will try to build these circuits, and attempting to do so isn't recommended.
Some of the applications where analogue multipliers may still be used include Military Avionics, Missile Guidance Systems, Medical Imaging Displays, Video Mixers, Sonar AGC Processors, Radar Signal Conditioning, Voltage Controlled Amplifiers and Vector Generators. While we tend to think that 'everything is digital' these days, that's not really the case at all. Analogue techniques are far from 'dead', despite the capabilities of modern computers.
The wattmeter described is a very good example. This can be done digitally, but it won't be as responsive as an analogue circuit, and will require custom software. This probably isn't especially difficult, but unless your programming skills are pretty good you're likely to find it far more difficult than you thought. Digital circuits traditionally use a digital display, which is not helpful for a piece of test equipment intended to monitor a dynamic signal.
The mathematical functions of integration and differentiation are easy to describe, implement and simulate in electronics, but they are difficult to calculate, since calculus is required. This is an area of maths that usually causes people to run in the opposite direction, because it's one of the most difficult. PID servo systems are hard to simulate, and in real life they can be difficult to get right. Integration and differentiation are functions that are very common in electronics, although in most cases there are short cuts (formulae that have been worked out for us) for specific applications.
The datasheets for the various devices were a major source of information, but the 1980 edition of 'Linear Applications' (National Semiconductor) solved the final puzzle when looking at simple opamp-based multiplier/ divider circuits. While there are circuits shown on the Interwebs, some are simply wrong, and they don't work as claimed (some not at all). Even a lengthy video I saw that supposedly 'explained' how these circuits function used a flawed circuit that doesn't work. This isn't helpful. Additional references are in-line, with others shown below ...
For some further reading, I suggest analogmuseum.org. This is one of many sites that discuss analogue computers, but most are old (hence the museum). New versions are less well documented, as they will often be subject to patent applications or other impediments to ready access.
 Main Index Main Index  Articles Index Articles Index |