

|
| Elliott Sound Products | Linear Power Supply Design |

 Main Index
Main Index
 Articles Index
Articles Index
Having searched the Web for reference material (and found very little!), this would appear to be the definitive article on the design of a 'simple' linear power supply for a power amplifier. Power supplies are needed for every type of amplifier (or any other electronic equipment for that matter) we will ever use. I do not intend to deal with 'esoteric' designs with interesting names, but the simple, unregulated linear power supply that is still the mainstay of audio power amplifiers. This specifically excludes switchmode supplies, which are a great deal more complex.
These linear supplies should not create any problems for anyone, because they are so simple, right? Wrong! They appear simple, but there are many inter-related factors that should be considered before just embarking on your next masterpiece. The purpose of this article is to explain the terminology used, traps and pitfalls, and give some insight by way of a few practical examples.
Most of the general principles described can be translated to higher or lower voltage or current with no change to the basic parameters. If the voltage is increased, you simply need to ensure the diodes are rated for the worst case PIV (peak inverse voltage) to which they will be subjected. This depends on the type of rectifier used, and is described in more detail further below.
One omission that will be apparent to many readers is any reference to valve (vacuum tube) rectifiers. Contrary to the firmly held beliefs of some, they have exactly zero sonic benefit in any design, but there are people who (for reasons that I can't determine) prefer the power supply to sag under heavy load. This is replicated easily by using resistors in series with silicon diodes, of a value similar to that found in the valve data sheet. For example, a 5AR4 has a typical plate resistance of around 50 ohms at 25mA plate current, and a silicon diode in series with a 50 ohm resistor will give virtually identical results. All valve rectifiers also impose an upper limit on the capacitance following the rectifier, and that usually means that the filter cap is far too small to provide acceptable filtering. Valve rectifiers have one (and only one) redeeming feature - they provide a 'soft start' as the filaments or heaters warm up.
Anyone who claims to be able to hear the difference between a valve and silicon diode rectifier is either suffering from wishful thinking or self-delusion. As always, any test must be double-blind or the 'results' obtained aren't worth the time spent obtaining them. All sighted tests (where the listener knows what s/he is listening to) are invalid, and this has been proven many times in many different disciplines. It must be possible to obtain a statistically significant result - getting the right answer 50% of the time is no better than guesswork.
You also won't find anything here that suggests or recommends ultra-fast or fast recovery diodes, because there's simply no point for 50Hz or 60Hz mains. However, as noted in section 9, they don't do any harm and if that's what you prefer then use them by all means. Fast diodes essential in switchmode supplies because they operate at anything from 25kHz up to 100kHz or more. They don't 'sound better' than ordinary diodes, and again, only double-blind tests will reveal if anyone can really hear the difference. Remember that the idea of a rectifier and filter is to produce DC which is then used by the electronics. The idea that one rectifier type supposedly sounds 'better' than another is quite silly. There is no evidence that there is the slightest difference to sound quality if fast diodes are used, despite countless unsubstantiated claims. In some cases you may get a small reduction in conducted emissions (high-frequency interference sent back into the mains wiring).
There is one application where fast diodes are definitely recommended, and that's for 'choke input' filters, where the diodes feed rectified AC to the filter cap(s) via an inductor. These are not covered here because they are extremely uncommon in modern equipment, although a superficially similar arrangement is often used in regulated switchmode power supplies.
For anyone who would like to run transformer power supply simulations, I suggest you read the article Power Supply Simulation (Not As Easy As It Looks), which covers the tricks you can use to make a simulator emulate the 'real world' performance of transformers and rectifiers.
It's important to understand that the so-called 'linear' power supply is not linear at all. Current is delivered from the transformer (and the mains) only when the AC voltage is greater than the stored charge in the filter capacitors. The waveform is highly non-linear and can inject noise into any wiring that's close by (including speaker cables!). Mains and other AC wiring should be kept well separated from all signal and speaker wiring. The 'ground' point must always be taken from the centre-tap of the filter capacitors for a split supply to prevent diode switching noise from being injected into the ground wiring. Never take the ground from the transformer centre-tap, even if there's only a few millimetres of wire between that and the filter caps. Likewise, DC must be taken from the filter caps, and not from the bridge rectifier.
You need to be aware that transformer secondary voltages are nearly always specified at full rated current into a resistive load. For example, a 100VA transformer is designed for an output of 30V RMS at 3.33A. When loaded with 9Ω, the secondary voltage will measure 30V RMS (if the mains voltage is the same as the rated primary voltage!), but when unloaded (no secondary current) the voltage will be around 33.5V RMS, giving a DC voltage of about 45V, including diode losses for a bridge rectifier. With a resistive load, the regulation is around 11.5% (compare this with the values shown in Table 4.1). When loaded with a bridge rectifier and filter caps followed by a load that takes the transformer to full load (24Ω) the DC voltage falls from 46V to 38V, which is a regulation of worse than 17%. This is completely normal, and it happens with all transformers.
As a result, all linear power supplies will provide more than the expected voltage with no (or light) load, and less than expected at full load. Failure to appreciate this is common, largely because most articles that describe linear power supplies either don't mention it, or it's glossed over expecting that "Everyone knows this". In reality, everyone does not know this, other than from their own measurements, which may (or may not) be sufficiently accurate. 'Knowing' something is very different from observing a phenomenon, but not understanding exactly why it happens.
Mains voltages are nominally 230V or 120V, but the actual voltage varies from hour to hour (and sometimes minute to minute). The tolerance is generally ±10%, but it's very common for that to be exceeded. Australian mains voltage is nominally 230V, but it's not at all uncommon to see up to 260V (+13%) and sometimes more (I've measured up to 265V RMS on occasion). Much the same occurs everywhere, and in some places the claimed 'accuracy' can be well over ±10%. If the input (primary) voltage changes, so too does the secondary voltage, in direct proportion. That's only one of the many reasons that your DC voltages are different from the theoretical values.
We expect a sinewave from the mains, but it not - it's invariably distorted. The degree of distortion varies throughout the day, and depends on the current loading on the grid. Section 5.1 gives more details, but it's fair to say that the 'rules of thumb' that we all use are either wrong, or at least inaccurate. Surprisingly perhaps (perhaps???), this doesn't matter very much, because the errors created by the basic formulae are smaller than the errors caused by mains variations and transformer winding resistances. So, you can continue to use √2 (and its inverse) and not worry about it. Provided you understand that the results are (very) approximate, then you're well on your way to understanding linear power supplies.
Power supplies themselves require several definitions (these are discussed later in this article), but the requirements of the amplifier that is to be connected need to be understood before we start. This makes a very big difference to the way the supply performs.
Poor earthing practices, such as connecting components to the nearest available ground reference can (and do) also create problems, and these can introduce hum, or more usually a 'buzz' into the signal circuits. This applies equally to Class-AB and Class-A amplifiers, but is usually more apparent with Class-A since the maximum current is drawn on a continuous basis. Transformer leakage flux can also cause buzz, so ensure that DC, speaker and signal wiring is kept well clear of any transformer. Toroids have lower leakage flux than E-I transformers, but they can (and do) still cause problems.
Because a transformer's flux density is highest at no (or light) load, any mechanical noise will be greatest at idle and with low audio levels, and this is exactly where people expect their equipment to be noise-free.
Class-AB Amplifiers
I shall refer to the standard power amplifier as Class-AB - of all the amplifier types, these are the most common. Any amp that draws a quiescent current through the output devices is by definition, Class-AB. For true Class-B, there is no quiescent at all, and the output devices will conduct for exactly 180 degrees - this is rare.
Class-AB amps have a very widely varying current drain, which may be only 20 - 100mA or so with no signal, but rising to many amps when driven. The main problem is the revolting waveshape of the current on each supply lead, typically half-wave pulses, in sympathy with the program content.
These waveforms - this is current, not voltage - have sharply defined transitions, and as such will generate a magnetic field which varies with the current. Since a sharp transition equates to high order harmonics, care must be taken to ensure that voltages are not induced into the input stages of the amp from the supply lines. Because of the low inductance of the wiring of an amp, these problems are going to create distortion components which will tend to be worse at higher frequencies.
It is not only the amplifier which creates current pulses, but the rectifier/ filter capacitor combination as well. The power supply rectifier diodes usually conduct for only a short time during each AC cycle - this may be as little as 3 or 4 degrees at idle, but both the angle of conduction and the amplitude of the current pulse will increase as more power is drawn from the supply.
Class-A Amplifiers
The other common amplifier type is Class-A. These amps draw a large current on a continuous basis, and place a completely different loading on the supply. The current pulses are gone from the supply leads, but the rectifier and filter now must handle the maximum current on a continuous basis. The output voltage will always be lower than expected - the old 'rule' about the DC voltage being equal to the peak of the AC voltage (RMS × 1.414) doesn't apply.
The continuous load creates a new set of constraints on the design of a power supply, and the use of a Class-A amp implies that the builder already wants the very lowest noise. Although the noise of the power supply DC output (hum/ ripple) will normally be low because of extensive filtering, regulation or a capacitance multiplier, the switching noise of the diodes in the rectifier can become more than a nuisance if proper care is not taken.
Class-D Amplifiers
Class-D amps in various forms are now common. Like Class-AB amps, the supply current varies widely with output level, but some don't have very good PSRR (power supply rejection ratio) so the DC needs to be well filtered. There is another problem as well, commonly referred to as 'bus-pumping'. This can be a significant issue with high power, low frequency output, and the topology of a typical single-ended (as opposed to bridged or BTL) Class-D amps means that the supply rail voltage increases, and can lead to overvoltage shutdown or amplifier failure.
Some Class-D amps rely on very large filter capacitors to absorb the power returned from the load, and others run two amplifiers in 'anti-phase'. As one drives positive, the other drives negative, and inputs and speaker connections are reversed in relation to the other channel. This is provided naturally by a BTL design. The anti-phase connection ensures that current is drawn from both supplies (+ve and -ve) simultaneously and prevents (or at least reduces) bus pumping.
Somewhat surprisingly perhaps, the fundamental requirements of the final design are not greatly influenced by the different loading presented by the different amp types described above. There are differences of course, but in most cases they don't change the basics of PSU design. The continuous rating of a Class-A amp means that you must design the supply for a continuous (rather than transient) current, but since we are discussing properly designed, quality power supplies, the final result may be quite similar. However, a continuous high current load always means the voltage will be less than expected.
When a power supply is used with an amplifier, the basic things we need to know before starting are as follows
Power output and minimum impedance, or ...
Peak / average current
Acceptable power supply ripple voltage
With only these three criteria, it is possible to design a suitable supply for almost any amplifier. I shall not be describing high current regulators or capacitance multipliers in this article - only the basic elements of the supply itself. These other devices are complete designs in themselves, and rely on the rectifier/ filter combination to provide them with DC of suitable voltage and current.
The first component of the power supply is the transformer. Using magnetic coupling between windings, the transformer is used to isolate the amplifier (and the users) from the mains voltage, and to reduce (for solid state equipment at least) the voltage to something the amplifier can tolerate. The primary winding will be rated at 240, 220 or 120V AC depending on where you live, and the secondary will be a more user friendly (or less user hostile) voltage to suit the amplifier.
Contrary to what you might imagine, the maximum flux density in a transformer core occurs with no load. This is covered in detail in the Transformers article, but it's mentioned again here because it's an important thing to understand. If you assume the 'alternative possibility', your understanding of transformer functions will lead to assumptions that are seriously at odds with reality.
DC Output: The DC output is approximately equal to the secondary voltage multiplied by 1.414, but as we shall see, this is a rather simplistic calculation, and does not take the many variables into consideration. At light loading, this rule can be applied without fear, and it will be accurate enough for most applications. When an appreciable current is drawn, this simple approach falls flat on its face.
Mains variations: These occur in all situations, and the mains voltage at any point in time will usually be somewhat different from the nominal voltage quoted by the supplier. Any variation of 10% or less can be considered 'normal', and greater variations are not at all uncommon. In nearly all cases, an amplifier is rated at a certain power output into a specified load impedance, and at the nominal mains voltage. For those who live close to a sub-station or pole transformer, expect the voltage (and power output) to be higher than quoted - the rest of us can expect a lower mains voltage and less power, especially during peak electricity usage times.
Losses: Since all transformers have losses, these can be ignored in the design phase for only the simplest and least critical applications. For anything where reasonable performance is expected, you need to do more work to get everything right.
Magnetising loss (AKA iron loss) is the current that is required to maintain the design value of magnetic flux in the transformer core. There is nothing you can do to affect this loss, as it is dependent on the size of the core and the design criteria of the manufacturer. Large transformers will have a larger magnetising loss than small ones of the same type, but will be less affected by it due to the larger surface area which allows the transformer to remain cool at no load. Small transformers (less than ~25VA) have a greater loss per VA than bigger ones, and this is one of the reasons that small transformers run quite warm even when unloaded.
The iron losses are greatest at no-load and fall as more current is drawn from the transformer. Copper losses are caused by the resistance of the winding, and are lowest at no load, and rise with increasing output current. There is a fine balance between iron and copper losses during transformer design. A relatively high iron loss means that copper losses will be reduced (thus improving regulation), but if too high, the transformer will overheat with no load. A full description of the magnetising current and its effect on regulation is outside the scope of this article, and since there is little you can do about it, it shall be discussed no further. More information is available in the articles about transformers. It's interesting (but more-or-less irrelevant) to note that a transformer core's magnetic flux density is greatest at no load, and reduces as the load is increased. Many people get this wrong and assume that the opposite must be true. It's not!
Mains noise: Noise can easily get through a transformer, both in transverse and common modes. Transverse noise is any noise or waveform distortion that is effectively superimposed on the incoming AC waveform, and this is coupled through the transformer along with the wanted signal - the mains.
Common mode noise is any noise signal that is common to both the active (hot) and neutral mains leads. This is not coupled through the transformer magnetically, but capacitively. The higher the capacitance between primary and secondary windings, the more common mode noise will get through to the amplifier. The much loved toroidal transformer is much worse than conventional 'EI' (Ee-Eye) lamination transformers in this respect because of the large inter-winding capacitance. An electrostatic shield will help, but these are uncommon in mass produced toroidal transformers. The conventional transformer is usually better, and by using side-by-side windings instead of concentric windings, common mode noise can be reduced by an order of magnitude.
Input mains filters can remove either form of high frequency noise component to some degree, and large spikes can be tamed using Metal Oxide Varistors (MOVs) that effectively short circuit the noise pulse, reducing it to a level that is (hopefully) inaudible. Contrary to the beliefs of some, there is no panacea for noise, and it is best attacked in the equipment, rather than the now popular (but mainly misconceived) notion that an expensive mains lead will cure all.
Regulation: When specified, regulation is based upon a resistive load over the full cycle, but when used in a capacitor input filter (99.9% of all amplifier power supplies), the quoted and measured figures will never match.
Since the applied AC spends so much of its time at a voltage lower than that of the capacitor, there is no diode conduction. During the brief periods when the diode conducts, the transformer has to replace all energy drained from the capacitor in the intervening period between diode conductions.
Consider a power supply as shown in Figure 1. This is a completely conventional full-wave capacitor input filter (it is shown as single polarity for convenience). The circuit is assumed to have a total effective series resistance of 1 Ohm - this includes transformer winding resistances (primary and secondary) and diode losses. The capacitor C1 has a value of 4,700µF. The transformer has a nominal secondary voltage of 28V.
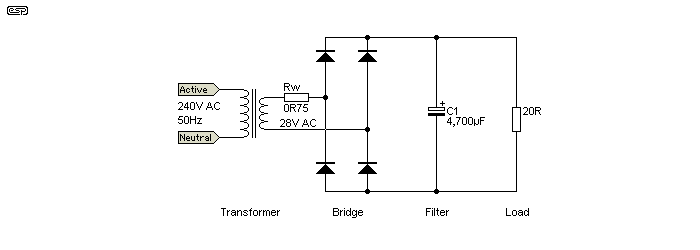
Figure 1 - Full Wave, Capacitor Input Filter Rectifier
The transformer is rated at 60VA and has a primary resistance of 15 Ohms, and a secondary resistance of 0.5 Ohms. This calculates to an internal copper loss resistance of 0.75Ω at the secondary (shown as Rw (winding resistance).
With a 20 Ohm load as shown and at an output current of 1.61A, diode conduction is about 3.5ms, and the peak value of the current flowing into the capacitor is 5.36A - 100 times per second (10ms interval). Diode conduction is therefore 35% of the cycle. RMS current in the transformer secondary is 2.98A.
Secondary AC Amps 2.98A RMS 7.0A Peak Secondary AC Volts (loaded) 26.39V RMS 35.11V Peak Secondary AC Volts (unloaded) 28.00V RMS 39.61V Peak DC Current 1.61A DC Voltage (loaded) 32.2V DC Voltage (unloaded) 38.45V DC Ripple Voltage 722mV RMS 2.24V Peak-Peak
Ripple across the load is 2.24V peak-peak (722mV RMS), and is the expected sawtooth waveform. Average DC loaded voltage is 32.2V. The no-load voltage of this supply is 38.45V, so at a mere 1.6A load, the regulation is ...
Reg (%) = ((Vn - Vl) / Vn) × 100
Where Vn is the no-load voltage, and Vl is the loaded voltage
For this example, this works out to close enough to 16% which is hardly a good result. By comparison, the actual transformer regulation would be in the order of 5% with a resistive load for a load current of 2.14A at 28V. Note that the RMS current in the secondary of the transformer is 2.98A AC (approximately the DC current multiplied by 1.8) for a load current of 1.61A DC - this must be so, since otherwise we would be getting something for nothing - a practice frowned upon by physics and the taxman.
The transformer's output voltage is no longer a sinewave - the tops are 'clipped' because of the high peak current. With an AC load current of 7A peak, the voltage loss due to winding resistance is determined by VLoss = RWindings × IPeak, which amounts to 5.25V peak that's 'lost' across the winding resistance when the diodes conduct. The reality is more complex than the simple calculation shows, but the DC output voltage is still reduced to 32V rather than the 38V expected. There is no simple formula to work out the loaded DC output voltage for a given current, and it's usually easier to measure it than to attempt a calculation. Simulation works, but only if you know the primary and secondary transformer winding resistances, and the diode forward voltage at the peak current (these are all difficult to measure!).
Output power is 32.2V × 1.61A = 51.8W, and the input is 28V × 2.98A = 83 VA. Input power is harder to measure and is the sum of the output power and all systems losses. For this example, we'll assume that the sum of the losses is 10W, so input power will be 62W.
So, if the input power is 62W and voltage times current is 83 VA, then the power factor is ...
PF (Power Factor) = Actual Power / Apparent Power = 62 / 83 = 0.75
There are many losses, with most being caused by the winding resistance of the transformer. The diode bridge accounts for an additional 2.5W at the current used for this test. Even the capacitors ESR (equivalent series resistance) adds a small loss, as does external wiring. There is an additional small loss as well - the transformer core's 'iron loss' - being a combination of the current needed to maintain the transformer's flux level, plus eddy current losses which heat the core itself. Iron loss is most significant at no load and decreases with increasing load.
Even though the transformer is overloaded, provided the overload is short-term no damage will be caused. Transformers are typically rated for average power (VA), and can sustain large overloads as long as the average long-term rating is not exceeded.
As described above, I assumed a total equivalent secondary series resistance for the transformer of 0.75 Ohm, which is about typical for a 60VA transformer as used here. Larger transformers will have lower series resistance (and vice versa), and the equivalent may be calculated - this is easier than actually measuring it under load.
If the secondary resistance is (say) 0.5 Ohm for a 240V to 30V transformer, it will be found that the primary resistance is (or should be) in the order of 15 Ohms. The actual figure will vary from one transformer type to another (e.g. 'conventional' EI (ee-eye) laminations versus toroidal).
The effective primary series resistance is calculated (approximately) by ...
Re = Rp / (Tr)²
Where Re is equivalent primary resistance, Rp is measured primary resistance, and Tr is the turns ratio (in this case, 240 / 30 = 8
Therefore ...
Re = 15 / 64 = 0.234 Ohm
This value is now added to the secondary resistance to calculate total series resistance. Please don't bother to e-mail to tell me that these figures are not correct - this is intended as a rough approximation - calculating actual values for transformers is worthy of an article in itself (which I am not about to write!  ). However, for most transformers the above will be surprisingly close to reality, and it's probable that measurement variances will exceed any small calculation error (which is mainly due to magnetising current). A well designed transformer will have (close to) equal equivalent primary and secondary resistances.
). However, for most transformers the above will be surprisingly close to reality, and it's probable that measurement variances will exceed any small calculation error (which is mainly due to magnetising current). A well designed transformer will have (close to) equal equivalent primary and secondary resistances.
The simple fact of the matter is that accuracy here is completely unimportant, as there is also series resistance in the mains power wiring from the power generation plant all the way to the power transformer primary winding. This is going to vary from one outlet to another and from one house to the next. Although it can be measured, it's is a completely pointless exercise since it will only be relevant for one household. Other factors are the actual supply voltage (nominal 120V, 230V, etc.) which varies widely from day to day and hour to hour.
For what its worth, the actual supply voltage was 233V when I measured the mains impedance at approximately 0.8 Ohms at my workbench - does this help?. We shall now do what everyone else does, and ignore it completely, not because it's unimportant, but because there's nothing we can do about it. As part of the design, allowance must be made to allow for the highest and lowest voltages that are likely to be encountered in normal use.
However - and again for what its worth - your 100W / 8 Ohm amplifier will be reduced to just over 90W, simply by connecting a 2400W heater to an adjacent power outlet, based on 0.8 Ohms mains wiring impedance and a genuine 230V supply voltage (before connection of the heater). The situation is likely to be slightly worse in the US, because the much lower AC supply voltage means that all currents are doubled for the same power. Yes, wiring is a heavier gauge, but other factors can come into play (such as termination resistance, a variable quantity at best).
An important distinction must be made between power (Watts) and VA. Power is a measure of work, and it is quite possible (common, actually) to have a situation where there is voltage and current, but little or no work. The product of voltage and current is Volts × Amps, or VA, and there is commonly a wide variance between VA and Watts. The ratio of watts to VA is called power factor, which has a maximum (and ideal) value of unity. If you have 100VA and 50W, the power factor is 0.5.
Various loads (capacitive or inductive) will draw current from the output of a transformer, amplifier or the mains supply. If the load is purely inductive or capacitive, there is no power (work) at all, even though the current may be quite high. Fluorescent lighting fixtures are renowned for this, where the current can be several times what was expected based on the power rating of the tubes.
This phenomenon is called 'power factor', and a power factor of 1 means that there are no power losses due to inductance or capacitance. Likewise, a power factor (PF) of 0 means that there is lots of voltage and current, but no power. In the case of fluorescent lighting, power factor correction capacitors are used to try to maintain the PF at as close to unity as possible. If this were not done, the wiring to the fittings (especially in large commercial buildings) will overheat, and a much greater load than necessary is placed on the local power sub-station, and indeed on the entire power grid. Electricity supply companies worldwide have the same problems, and in most countries, there is legislation that determines the minimum acceptable power factor for any installation.
The switch mode power supplies used in computers have a very poor PF, but there are many new designs that improve this. These can be expected to become mandatory in the not too distant future, as a poor power factor makes electricity more expensive to supply, and therefore more expensive for the consumer.
Note that I do not propose to cover the topic of power factor in depth (in fact that was it!), but a basic understanding is useful, and will make some of the following information more sensible. For those who really want to know more, see Power Factor, Active Power Factor Correction and Reactance. These articles discuss power factor in depth.
A power transformer does not care if work is being done at the output or not. It has internal resistance and inductive losses, and cares only about the input voltage and current. A power transformer can be overloaded and destroyed by a large capacitance directly across the output terminals. The capacitor does not even get warm, since it dissipates no power and does no work. The transformer 'sees' only the load current, and heats up proportionally - if the VA rating is exceeded consistently, the transformer will eventually overheat and die.
Equally, a transformer may be operated at 500% of its ratings for a short period, and as long as it has enough time to cool down between overloads, will be unaffected by the ordeal. Unfortunately, this otherwise useful characteristic is pointless in audio, since the voltage will fall too far with the load, and amplifier power output suffers badly. Having said this, most 'mainstream' power amps will economise on the transformer, and rely on the duty cycle of typical programme material to provide an adequate supply voltage for normal music signals. The continuous (erroneously called 'RMS') power will be lower, sometimes significantly.
The term 'dynamic headroom' used to be used to describe the difference between continuous and peak output power. A large figure (2dB or more) indicates that the transformer is too small for the job, since the supply voltage collapses under a sustained load.
Because we are going to use the transformer in an unfriendly manner, with a rectifier and large capacitance as the load, the VA rating is much higher than the power rating of the amplifier may indicate. There are some basic rules of thumb for the most common rectifier types, and these are shown below.
The following table is from the second transformer article (Transformers - The Basics - Part 2). It's so useful that it's worth repeating, and covers toroidal transformers. E-I types will be heavier for the same rating, and the figures shown will be a little different.
| VA | Reg % | RpΩ - 230V | RpΩ - 120V | Diameter | Height | Mass (kg) |
| 15 | 18 | 195 - 228 | 53 - 62 | 60 | 31 | 0.30 |
| 30 | 16 | 89 - 105 | 24 - 28 | 70 | 32 | 0.46 |
| 50 | 14 | 48 - 57 | 13 - 15 | 80 | 33 | 0.65 |
| 80 | 13 | 29 - 34 | 7.8 - 9.2 | 93 | 38 | 0.90 |
| 120 | 10 | 15 - 18 | 4.3 - 5.0 | 98 | 46 | 1.20 |
| 160 | 9 | 10 - 13 | 2.9 - 3.4 | 105 | 42 | 1.50 |
| 225 | 8 | 6.9 - 8.1 | 1.9 - 2.2 | 112 | 47 | 1.90 |
| 300 | 7 | 4.6 - 5.4 | 1.3 - 1.5 | 115 | 58 | 2.25 |
| 500 | 6 | 2.4 - 2.8 | 0.65 - 0.77 | 136 | 60 | 3.50 |
| 625 | 5 | 1.6 - 1.9 | 0.44 - 0.52 | 142 | 68 | 4.30 |
| 800 | 5 | 1.3 - 1.5 | 0.35 - 0.41 | 162 | 60 | 5.10 |
| 1000 | 5 | 1.0 - 1.2 | 0.28 - 0.33 | 165 | 70 | 6.50 |
The primary resistance for all of the examples in the above table was calculated - this figure is rarely given by manufacturers. Resistance is shown for both 230V and 120V primary windings. Knowing the basics at this level is often very handy - you can determine the approximate VA rating of a transformer just by knowing its weight and primary resistance. The secondary resistance can be calculated from the primary resistance and the turns ratio. The result obtained by using nominal turns ratio (based on the stated primary and secondary voltages) is accurate enough for most purposes. As shown by the range provided, the primary winding resistance could be up to 15% lower than calculated to reduce the current density in the primary. (See Reusing Transformers for another table covering a wider range of VA ratings.)
To properly see the effects of the losses and currents involved, a simpler circuit will be used from this point. This consists of a 25V RMS 'ideal' generator, and the copper losses are simulated by a resistance. Since the full-wave bridge rectifier is a very common configuration, this is what shall be used for the detailed analyses that follow. There are variations and exceptions to everything, but simulations and real-life testing on these simple circuits are very close, so this is what shall be used.
A simple resistance is the load, and we shall see the vast differences in peak AC current, capacitor ripple current and output voltage as the various parameters are changed. A solid understanding of the behaviour of the transformer, rectifier and filter capacitor is essential if worthwhile power supplies are to be designed.
Figure 2 shows the voltages and currents present in a typical supply. The waveforms will be examined shortly - for now we are interested in the average current and voltage in each section of the supply. The generator voltage is 25V RMS, and for this supply I have used a secondary winding resistance of 0.75 Ohm - roughly equivalent to a 120VA transformer. The voltages and currents are all RMS - although in practice very few RMS meters can give an accurate reading of the spiky current waveform.
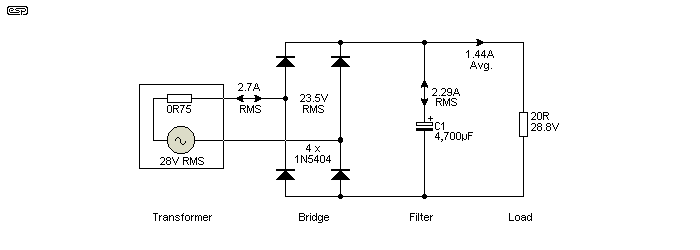
Figure 2 - Basic Bridge Rectifier - Voltages and Currents
Note the big difference between DC output current, capacitor ripple current and AC input current. The important parameters are listed in the table below ...
| Parameter | RMS (AC)/ Average (DC) | Peak |
| AC Voltage | 23.55 V | 31 V |
| AC Current | 2.71 A | 6.40 A |
| DC Voltage | 28.9 V | - |
| DC Current | 1.44 A | - |
| Ripple Current | 2.29 A | 4.95 A ** |
| Ripple Voltage | 655 mV | 2.08 V (P-P) |
** This figure is somewhat misleading, since there is both a charge and discharge cycle. During the discharge, there is a relatively constant current of -1.44A (the negative means the current is flowing out of the capacitor). During the charge period, the rectifier takes over the supply of current to the load and re-charges the capacitor at the peak current shown.
The average value is used for DC, and RMS for AC. Input VA (volts × amps) is 25V × 2.7A, or 67.75 VA, input power is 49.5W (simulated), and output power is 41.8W, so in all, 7.7W has been lost in the rectification and filtering process. Overall power factor is determined by ...
PF = Power / VA
PF = 49.5 / 67.75 = 0.73
The power factor on the transformer primary will be very close to that shown for the secondary with a good quality transformer. Power factor is not considered to be especially important for linear power supplies suited to audio applications, because the average power is quite low. This changes for industrial applications, because many large power consumers are charged extra if they do not maintain a power factor of at least 0.9 (resistive loads have a unity power factor, which is ideal).
About 5.5W is lost as copper losses in the transformer (dissipated in the 0.75 ohm resistor that simulates the winding resistances). Each diode dissipates around 550mW (a total of 2.2W for all 4 diodes), making the total loss 7.7W as shown above.
Attempting to quantify each individual loss is a relatively pointless exercise, since the end result is to make a power supply that works - we can do nothing about the losses. In reality, the losses may different from those calculated, since the RMS values are based on a pure sinewave input - this is somewhat dubious (although quite OK for the purpose of this article) because mains power is never a perfect sinewave.
About 0.7 to 0.9V is lost across each diode during conduction, but this will vary in practice, based on the current capacity of the rectifier diodes. Since this is a bridge rectifier, there are two diodes conducting at the +ve and -ve peaks of the waveform, so the total voltage loss is 1.8V - so the output DC should be around 32V. The measured values of 23.55V AC and 28.9V DC are a direct result of the waveform distortion. Because current is drawn only at the peak of the AC waveform, the input to the rectifiers is not a sinewave. The voltage and current waveforms are shown below, and it can be seen that the voltage waveform has been 'flattened' at the peaks. This is due to the high peak current drawn during this time, and no voltmeter will give the correct value - you must use an oscilloscope to be able to measure the peak-to-peak value of the waveform.
You may not have picked it up straight away, but look at the voltage waveform in Figure 3. It's no longer a sinewave, and the RMS voltage is not the peak voltage divided by 1.414 - the 'standard' formula has failed you! The peak voltage is 31V, but the RMS voltage is 23.55V, a fairly significant error (1.63V) from the standard √2 ratio we've all been led to believe. Somewhat unexpectedly perhaps, a similar error is normal with the mains supply, as it's not a sinewave either! The mains will almost invariably show a similar 'flattening' at the waveform peaks, so while a 'true RMS' meter will give you the right reading, using √2 to determine the DC voltage will be wrong. "Bugger!" said Pooh, as he threw all his multimeters in the bin  .
.

Figure 3 - Voltage and Current Waveforms
This reveals additional information to the voltage and current measurements taken before. Both are essential in understanding the rectification process. The peak AC input is only 32V, where we would normally expect 25 × 1.414 = 35V. We appear to have some missing voltage (35V - 1.8V diode drop is 33.2V), not the 28.9V DC measured with a multimeter. Examination with an oscilloscope and measuring peak currents (either simulated or using a current probe), we find that the voltage drop across the transformer winding resistance is much greater than expected due to the current peaks of 6.4A. This causes an internal voltage drop of 4.8V ... not the 2V that may have been assumed based on a resistance of 0.75 ohms and an average current of 2.71A.
An oscilloscope shows that the peak DC voltage is higher than the average value shown by the meter, and is 29.96V ... everything really does fall into place, but only when the whole process is examined carefully. You will never really understand the entire process unless you examine each of the many contributing factors.
Note that the waveforms of Figure 3 were taken at different locations within the circuit, and are in phase. The positive going part of the output ripple voltage, the peaks of the AC current, the positive peaks in capacitor ripple current and the flattening of the AC input voltage all occur at exactly the same time.
There are no 'simple' answers to the difference between AC and DC current. It depends on the type of rectifier, the value of capacitance used as the main filter cap, and the nature of the load. Dynamic loads are the reality for amplifier supplies, but there's no way to determine a 'typical' dynamic load because it depends on the music programme material. Low frequencies tend to have wider dynamics than midrange or treble, but that's almost impossible to simulate in any meaningful way.
Useful analysis can only be done with a static load, and I've used an estimation based on half the maximum steady-state 'RMS' power output of a single amplifier using ±35V supplies (100W into 4Ω). The load used for each example shown is based on a dual supply (positive and negative outputs), delivering a total output power of (close enough to) 50W with a total nominal voltage of 70V (2 × 35V). A stereo amplifier simply increases the load seen by the transformer, rectifier & filter.
| Rectifier | AC RMS | DC Average | Ratio |
| Bridge | 1.89 A | 740 mA | 2.55 |
| Full Wave | 1.89 A | 740 mA | 2.55 |
| Doubler | 3.67 A | 730 mA | 5.0 |
| Half Wave Note 1 | 2.34 A | 722 mA | 3.24 |
Note 1: Although the half-wave rectifier looks ok, the transformer current is unidirectional and will cause core saturation in any transformer, leading to failure in short order! A toroidal transformer will blow the mains fuse almost instantly, while an E-I transformer may take a few seconds before the fuse blows. Not using a fuse will cause transformer failure.
As noted in several places, half-wave rectifiers are not recommended for any power supply, and they should not be used if the current expected is more than a few milliamps. I never use half-wave rectifiers for a power supply, regardless of output current. I suggest that the reader takes a similar view - there's no need for simplicity when diodes are so inexpensive!
These results are all 'steady-state' and do not include inrush current. The exact difference depends on many factors, and should only be considered as a guide. It's quite obvious that the AC (RMS) current is always greater than the DC (average) current, but the only circuit one would normally use for a dual supply is the dual full-wave bridge rectifier. In some cases the supply will use a 'dual mono' arrangement (two transformers, bridge rectifiers and filter caps), but this doesn't change anything by much. It does mean that you use more diodes (or a pair of bridges), but it doesn't affect the underlying physics.
While these calculations indicate that the transformer's VA rating has to be higher than you'd expect, in reality music is sufficiently dynamic that even an apparently under-rated transformer is often quite alright, provided the amplifier isn't driven to clipping on a more-or-less permanent basis (as can happen with guitar amplifiers). You will also see that the values shown here are different from those shown in Table 5.7 - the latter shows the commonly accepted AC vs. DC current, while the values above were determined by simulation. The transformer's winding resistance is a dominant factor in the ratio between AC and DC current, so larger transformers (for a given load) will show a greater difference between the AC (RMS) and DC (average) current.
It is well known that bigger transformers have better efficiency than small ones, so it is a common practice to use a transformer that is over-rated for the application. This can improve the effective regulation considerably, but also places greater stresses on the filter capacitor due to higher ripple current. This is quoted in manufacturer data for capacitors intended for use in power supplies, and must not be exceeded. Excessive ripple current will cause overheating and eventual failure of the capacitor.
Capacitor ripple current ratings can be ignored at your peril, but in an audio amplifier reproducing music the average current will be considerably less than the worst case figure.
Large capacitors usually have a higher ripple current rating than small ones (both physical size and capacitance). It is useful to know that two 4,700µF caps will usually have a higher combined ripple current than a single 10,000µF cap, and will also show a lower ESR (equivalent series resistance). The combination will generally be cheaper as well - one of the very few instances where you really can get something for nothing. Using ten 1,000µF caps will generally give even better overall figures again, but the cost (in time and effort) of assembling them into a proper filter bank may not be felt worthwhile.
Above a specific value, as the capacitance is increased, the peak charging current will remain much the same for the same sized transformer, but the capacitor retains more of its charge between cycles. The switch-on current will be very much higher, and the surge will last longer as the capacitor charges. At capacitor values below optimum, the peak charge current will decrease somewhat, but there will be far greater output ripple.
There is no hard and fast rule for determining the optimum value for the filter cap, but in general I would suggest that the value should be at least that required to give a full load ripple voltage of less than 5V peak to peak. Based on this, my recommendation is that the minimum value is 2,000µF per amp DC, so a 5A (continuous) power supply will have a minimum of 10,000µF capacitance.
What is achieved by increasing the capacitance is the ability of the capacitors to retain more of their charge between AC cycles. Since the current demands of a Class-AB amplifier vary so widely - with the majority of the time at very low average currents - the actual operating voltage will be closer to the no-load voltage.
With large capacitors, the momentary current peaks created by the programme material will not be of sufficient duration to discharge the caps to the full load voltage levels, so there is more voltage available on a more or less consistent basis. This equates to more power for transient signals, and lower ripple voltages the rest of the time.
With a 4,700µF capacitor and a peak current of 5A (equivalent to the peak current of a 100W amp into 8 Ohms), the capacitor will lose voltage at the rate of 1V / ms between 'charges'. As the capacitance is increased, this discharge rate naturally falls proportionality to the capacitance. Doubling the capacitance halves the discharge rate and the ripple voltage for a given current, but increases the capacitor ripple current and the peak AC current - although the average value remains much the same. There are some small variations, but these are eventually accounted for if we analyse the waveforms critically - again, this is a relatively pointless exercise, and will not be undertaken.
What we will do, is see what happens in each individual case when ...
Table 2 shows the currents and voltages with the same transformer used in Figure 2, but with a 10,000µF filter cap. There are insignificant increases in currents, and no worthwhile increase in the average DC output voltage. Output ripple is half that of the previous example. As can be seen, more capacitance will affect the DC ripple voltage but little else, and one may wonder if it is worth the effort (the answer is generally "yes", but it depends on the application).
| Parameter | RMS (AC)/ Average (DC) | Peak |
| AC Voltage | 23.6 V | 31 V |
| AC Current | 2.71 A | 6.27 A |
| DC Voltage | 28.8 V | - |
| DC Current | 1.44 A | - |
| Ripple Current | 2.29 A | 4.8 A |
| Ripple Voltage | 306 mV | 1 V (P-P) |
Table 3 is the same data, with the original 4,700µF capacitor, but now with a transformer having 0.5 of the original total winding resistance (0.375 ohms) - this is equivalent to a transformer of about 4 times the 120VA rating used before (or about 500 VA).
| Parameter | RMS (AC)/ Average (DC) | Peak |
| AC Voltage | 24.2 V | 32 V |
| AC Current | 3.15 A | 8.32 A |
| DC Voltage | 30.3 V | - |
| DC Current | 1.52 A | - |
| Ripple Current | 2.76 A | 6.8 A ** |
| Ripple Voltage | 731 mV | 2.2 V (P-P) |
The increases in both average and peak currents are quite substantial, and the output voltage is higher by a small (but not especially useful) amount. The DC current is higher, only because the voltage is greater, and this is the sole reason for the increase in ripple voltage. The big test is to use the 10,000µF filter cap with this very much larger transformer, and see what increases occur.
| Parameter | RMS (AC)/ Average (DC) | Peak |
| AC Voltage | 24.2 V | 32 V |
| AC Current | 3.15 A | 8.52 A |
| DC Voltage | 30.4 V | - |
| DC Current | 1.52 A | - |
| Ripple Current | 2.79 A | 7.0 A ** |
| Ripple Voltage | 345 mV | 1.16 V (P-P) |
There's a small increase in the peak current from the transformer, but not enough to cause the slightest concern. The RMS value is unchanged, and there is the expected reduction of ripple voltage. Capacitor ripple current is increased a little, but it's nothing to worry about.
In case anyone is wondering why I used a load resistance of 20 Ohms, this was to simulate one half of a 55W Class-AB amplifier operating at the onset of clipping into an 8 Ohm load, with a steady sinewave input. Any dynamic analysis is very difficult, and the results are not particularly meaningful unless the exact signal source is known, along with the specifics of the power amplifier that is connected to the supply.
In these calculations, I also made no allowance for the fact that nearly all transformers are rated for an output voltage at full current - this is invariably the voltage into a resistive load, and not a rectifier / filter combination. This means that the voltage will always be a little higher than specified at no load, and now you know why the DC is less than expected at full load.
I only heard about this myth a couple of years ago (at the time of writing), and while I can imagine how it came about, it's completely bogus. Some people claim that as the capacitance is increased for a given sized transformer, the peak current is also increased. There are conflicting additional claims that the RMS input current to the transformer either A) does, or B) does not increase as well. Added to this is a further claim that the transformer will overheat because the current is higher.
In essence, this is all complete rubbish. Incorrect measurement techniques or bad simulation practices may lead one to believe that this is the case, but it is not. The important thing is that we can only examine the steady state current - inrush current will quite obviously be greater with larger capacitance, but this is a transient event. Because transient events are just that - transient - there is no point analysing them and making absolute claims, because every transient will be different. Transformers can survive massive short term overloads without any harm, and a soft start circuit will tame the transient currents to something less scary.
The steady-state conditions are applicable to most power supplies within about 100ms after power is applied, but to be safer it's better to allow 10 seconds or more. If one were to use a 2 Farad capacitor on a 15VA transformer, this time will be extended considerably, but this would be silly, and we are not interested in the effects of silly combinations.
If we use the transformer/rectifier circuit described above as an example, we can either measure or simulate the effects of using a much larger than normal capacitor. As shown in Figure 2, the selected capacitor is 4,700µF and the load current is 1.44A - all fairly normal. The transformer secondary current is 2.7A RMS, so a 120VA transformer is well within its ratings. Even overloads are not a problem - if they are infrequent, the transformer will be perfectly happy as long as it has a chance to cool down so its maximum temperature is never exceeded. A fan can be used to increase the VA rating of most transformers, albeit with some variability.
No problems so far. However, many audiophile expectations will demand that the capacitance be at least 10,000µF, around 50,000µF for passable performance, but (of course) 100,000µF would be much better. This is (IMO) rather pointless. I won't argue with 10,000µF, but any more is usually wasted and should not be necessary.
Now, according to the myth (sorry - 'theory'), this extra capacitance will cause the transformer's RMS current to increase, accompanied by a dramatic increase (or not) of the peak current - all during steady state conditions. It simply doesn't happen that way.
Adding more capacitance will ...
What is sensible? As with all things, it depends on the context. For a 25V transformer providing a worst case rectified and smoothed current of 1.44A into a 20 ohm load (as described above), a sensible upper limit would be perhaps 50,000µF, although even 100,000µF will cause no harm. Sensible values are those that consider the law of diminishing returns, where, after a certain point is reached further increases yield little additional benefit.
If we do an analysis of the different capacitor values whilst keeping everything else the same, the effects can be seen quite clearly. The table below shows a range of capacitor values, the transformer RMS secondary current, peak current, diode conduction period. load power and ripple voltage. As capacitance is increased, the load power also increases. Because the DC voltage has less ripple, the average voltage is very slightly higher. As a result, the load resistor dissipates a bit more power, and this accounts for the small increase in RMS current (remember, you can't get something for nothing).
| Cap Value | Isec RMS | Isec Peak | Diode Conduction | Load Power | Ripple (P-P) |
| 4,700 µF | 2.65 A | 6.18 A | 3.58 ms | 40.89 W | 2.008 V |
| 10,000 µF | 2.66 A | 6.21 A | 3.63 ms | 41.05 W | 953 mV |
| 22,000 µF | 2.66 A | 6.22 A | 3.63 ms | 41.08 W | 432 mV |
| 50,000 µF | 2.66 A | 6.23 A | 3.64 ms | 41.09 W | 191 mV |
| 100,000 µF | 2.66 A | 6.23 A | 3.64 ms | 41.09 W | 96 mV |
As you can see, the RMS input current difference is very small for steady state conditions. Inrush current is another matter though, and we need to examine that to ensure that nothing is stressed so much as to cause failure after a few years of operation. Before we do that, it is fairly clear that the law of diminishing returns is in full effect with any capacitance above 10,000µF. The increase in load power is negligible for the higher values, but ripple voltage is reduced. For a given load current, doubling the capacitance halves the ripple voltage. The (very small) increase in diode conduction time is due to the non-zero resistance of the source (the transformer winding resistances). While this is real, it's not something you need to worry about. A lower source resistance will make the conduction time increase more noticeable, but it still doesn't matter and there's nothing you can do about it anyway.
The figures shown here are an example, based on the schematic shown in Figure 2. Anyone wanting to do so can repeat the simulations I did, but for a steady state measurement, you must ignore the first part of the waveform with the inrush current. If this is included in an RMS analysis, you will not get the proper steady state value, but a value that includes the steady state and inrush currents. This is simply the way 99% of simulators work. For the figures shown, I ran the simulator for 2 seconds, and ignored the first 1.9 seconds. Data was only shown (and measured) for the last 100ms. If the entire 2 second simulation's data were used, the RMS current for a 100,000µF cap will be incorrectly shown as 5.64A, which is quite clearly wrong.
If you wish to simulate the myth in action, all you need is an ideal (zero ohm output impedance) voltage source and ideal diodes. Neither of these are actually available in the real world, but you can pretend. With these imaginary components, everything is different, and bigger caps cause huge increases in peak current. Since this has nothing to do with reality, it can be ignored. As noted, Table 5 was compiled from simulation data based on the circuit shown in Figure 2, using a non-zero source, and non-ideal diodes. Once the simulation has some vestige of reality to work with, we get answers that will match measured results remarkably well.
| Cap Value | ½ Cycle Peak | Duration to ... 50% of Max. |
Duration to ... Steady State |
| 4,700 µF | 24 A | < 1 cycle (20 ms) | < 40 ms |
| 10,000 µF | 30 A | < 1 cycle (20 ms) | 65 ms |
| 22,000 µF | 36 A | < 30 ms | 200 ms |
| 50,000 µF | 39 A | 65 ms | 345 ms |
| 100,000 µF | 41 A | 125 ms | 425 ms |
The first value is the capacitance, followed by the transformer secondary current for the first half cycle. It does not include the transformer's inrush current. The peak secondary current is limited to a maximum value based on the ...
This isn't easy to work out with any accuracy, but you don't need exact figures. As long as you have an overall understanding of the process and ensure that parts can handle the peak current without failure you don't need to go any further. Consider using a Project 39 soft start circuit to minimise the combined effects of transformer and capacitor inrush.
The third value is the time before the peak current has fallen to half the maximum. This was included to give you an idea of the duration of the inrush surge. The fourth column is an estimation, and shows the time from switch-on until the surge current has fallen to within 10% of the steady state value.
Needless to say, these tests are also easily run using a real transformer, diode bridge, filter cap and load. The figures will be slightly different, but the overall values will show exactly the same trend as shown. The transformer current waveform is best monitored across a low value resistor, with 0.1 ohm being about right. This will have a small effect on the peak current measured, but the measurements will correlate very well with those shown here. Alternately, measure the mains input current to the transformer using either the Project 139 or Project 139a mains current monitor. Either of these is better (and a great deal safer) than a resistor.
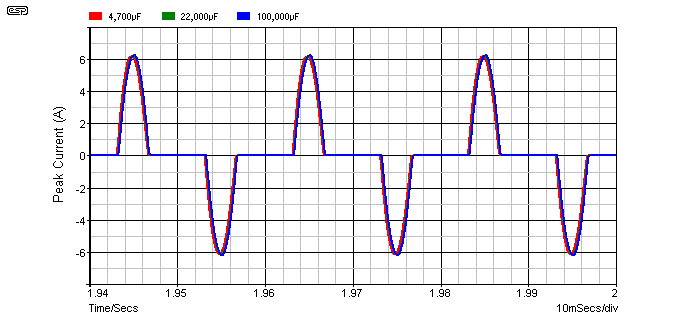
Figure 4 - Peak Current Waveforms
Figure 4 shows the peak waveforms with 4,700µF, 22,000µF and 100,000µF. They are all at the same scale, and all were taken after 1.9 seconds to ensure that the steady state conditions had been reached. As you can see, it is almost impossible to tell them apart, because they are almost perfectly overlayed. Since the peak values are almost unchanged, so too is the RMS value. The AC input voltage and load resistance are the same for each trace.
While it may seem that a higher capacitance should draw larger peak currents, it must be understood that the larger capacitor discharge less between charge pulses, and ultimately require exactly the same 'top-up' energy as a smaller cap. This effect can be seen just by looking at the ripple voltage figures - with lower ripple voltage, there is less voltage change when the diodes conduct, so the peak current and waveform remain relatively constant.
If the capacitor is smaller than optimum, then there will be very large differences between various values. Smaller than optimum is absolutely not recommended, and peak to peak ripple voltage should be no more than 10% of the total supply voltage for best results. The 4,700µF cap just makes it, and for normal listening would be perfectly alright.
So far we have looked at the full wave bridge rectifier, and this is but one of several different configurations. The most common (and/or simplest) rectifiers are ...
There are others, but they are not commonly used in low voltage amplifiers. The dual full wave (using a bridge rectifier and a centre tapped transformer) is probably the most common of all, and some further analysis of this rectifier will be covered next. I have chosen to ignore half wave rectifiers (in all their forms), but decided to add voltage doublers. These are normally only useful for low power applications where their operation is not critical. This is especially true of preamp supplies, which will almost always be followed by a regulator.
Half wave rectifiers should never be used. At any appreciable current (more than a few milliamps), the half wave rectification process means that the transformer is also subjected to a half wave rectified current, and this can cause the core to saturate at surprising small currents - especially with toroidal transformers. In general, avoid the use of half wave rectification altogether. There is no application that benefits from the use of a half wave rectifier.
A toroidal transformer can easily be pushed into hard saturation with as little as 20mA or so of DC in the windings. With any appreciable DC component, the input current rises dramatically, and it can easily exceed the transformer's full load rating. If sustained, this will cause the transformer to overheat and fail unless it's protected with an auto-resetting thermal cutout. If not, it's a very expensive experiment.
The full wave voltage doubler is still common in valve amplifier circuits and for some preamp supplies, and is very common with switchmode power supplies. For example, the Project 05 preamp supply offers a full wave voltage doubler as an input option. More on this below.
Of the major types, the generally accepted voltage and current ratios are as follows. These are not firm rules, only guidelines, and actual results depend on winding resistance and filter capacitance value. Even the impedance of your household mains supply makes a difference. (And no, stupidly expensive 'audiophool' mains leads don't help at all.)
| Rectifier Type | Filter Type ¹ | RMS AC Input | Diode Voltage |
| Full Wave (CT) | Capacitor Input | DC x 1.2 | AC Peak x 2 (from CT) |
| Full Wave (CT) Dual | Capacitor Input | DC x 1.8 ² | AC Peak x 2 (from CT) |
| Bridge | Capacitor Input | DC x 1.8 | AC Peak |
| Full Wave Doubler | Capacitor Input | DC x 3.3 | AC Peak x 2 |
1 Choke input filters have not been included, since although they provide superior filtering and lower noise, they are very expensive to produce because of the sheer size of the inductance.
2 This figure is for a dual supply (positive and negative outputs as shown in Figure 6). The load is between positive and negative.
As can be seen from the circuits analysed so far, the figure for bridge rectifiers (AC current 1.8 times the DC current) is close enough to what was measured. It must be remembered that this is not an exact science, since there are so many variables to deal with. The figures above are a guide only, and for continuous high current loads you need to ensure that the transformer won't be overloaded. This requires careful analysis and testing, because it's far more complex than it may appear.
The diode voltage rating is important, and must be considered in all cases. For most transistor amps, bridge rectifiers with a 400V rating are cheap and readily available in several current ratings, but for high voltage applications you need to be aware of the maximum voltage that can appear across each diode.
The bridge rectifier requires the lowest voltage diodes. Their reverse voltage rating only needs to be higher than the peak of the AC (VRMS x 1.414). For all others (including half wave), the diode voltage must be at least double the AC peak (measured from the centre-tap to either end of the winding). This becomes very important for high voltage supplies, and in some cases it's necessary to use two diodes in series to prevent failure. For example, a 600V DC supply from a full-wave rectifier (centre tapped transformer) requires diodes with a voltage rating of at least 1,200V and it's wise to use two 1kV diodes (e.g. 1N4007) in series for each diode.
Unlike the bridge rectifier which uses 100% of the transformer winding at all times, the full wave rectifier uses only half of the winding on each half cycle of the AC waveform. This leads to some additional losses, since the winding must have double the number of turns of that for a bridge rectifier. This means that the winding resistance is typically double that for a bridge rectifier, because the windings must be thinner so as not to occupy more area in the winding window. This leads to higher resistive losses.
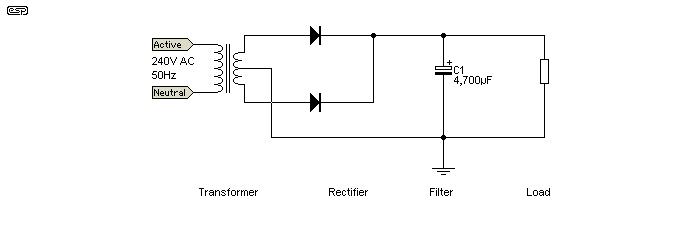
Figure 5 - Full Wave Rectifier
I have reverted to a transformer for this section, rather than the simulated version used before. This makes the drawings clearer, and the same depth of analysis will not be performed again this time. The capacitor ripple current is unaffected in principle, except that it will be slightly lower for a given VA rating since it is directly related to transformer winding resistance.
For the example in Figure 5, the AC current in each winding is 1.82A for a 1.47A DC load. This is quite close to the ratio of 1.2:1 shown in Table 5, and the difference is the result of normal variations in transformer winding resistance.
The VA rating for the transformer is the same for bridge and voltage doubler types, but is a little higher for the full wave. Despite apparent variations, wasted power is restricted to diodes and transformer winding resistive losses, and this assumes that windings are properly sized in all cases.
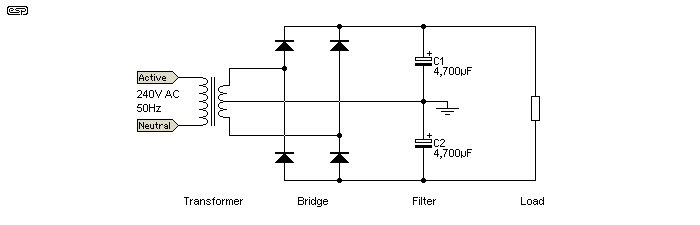
Figure 6 - Full Wave Centre Tapped Rectifier, Dual
This version now uses the entire winding all the time - each winding is used for both positive and negative supplies. Full winding utilisation means that the AC current is now the same as for a bridge rectifier, at 1.8 times the DC current, but only for a common mode load (i.e. between the supplies, rather than from one supply or the other to ground - this is identical to equal current from each supply to ground). Where the load is from only one supply or the other, the 1.2 rule applies, but power amplifiers will draw from both supplies (more or less) equally. The frequency of the signal waveform is mostly above the power supply input frequency, so the supply will effectively be loaded as common mode. All dual power supply designs must assume this load, or the result will be most unsatisfactory.
This type of supply often has a bad reputation, and is considered useful only for certain applications. Typically, the efficiency and regulation are considered by many to be rather poor, so it often tends to be used only for comparatively low current supplies. This need not be the case though. Because only half as many turns are needed, the wire can be twice the diameter, and will have ¼ of the resistance of a winding for a bridge rectifier. If this is done, performance is almost identical to a bridge. The doubler used to be a common supply in valve amplifiers (although not centre-tapped as shown below), since it halves the voltage across each capacitor and allows the use of lower voltage caps. They do need to have twice the capacitance though because the caps are in series, so the total capacitance is half that of each individual cap (hence the 10,000µF caps instead of 4,700µF as used before).
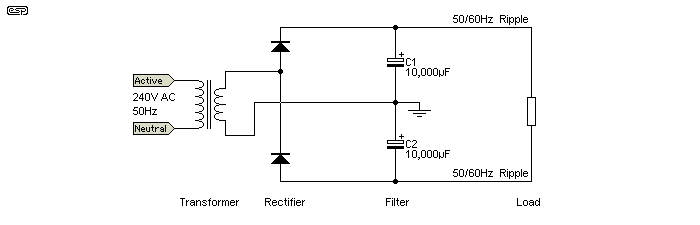
Figure 7 - Full Wave Voltage Doubler
Using the same voltage and load current as before, we can do a quick analysis of the circuit. The first thing to know is that the ripple voltage frequency at the centre tap of the two caps is the same as the applied mains (50 or 60Hz). Ripple at the main output is 100/120Hz, but only if the -Ve output is the earth/ ground reference. When used as a centre-tapped (+/- supply) with the centre tap grounded, the ripple voltage at each output (i.e. +Ve and -Ve) is at the mains frequency, but each output has the opposite phase for the ripple. This accounts for the 100/120Hz ripple when one side of the supply (not the centre tap) is grounded.
The voltage only manages to get to ±26.8V with a 1.5A load (actually a little less - about 1.49A). The ripple voltage is 2.3V peak-to-peak, but the AC input current is now slightly over 4.9A RMS. With a 25V winding and that much current, the transformer now has to be rated at 122.5VA, while delivering a fraction under 80W to the load. It should be quite apparent that this is not a particularly good way to build a power supply for high current, and in general my recommendation is that it be used only for relatively low current supplies.

Figure 8 - Full Wave Voltage Doubler, Single Ended
When used in valve (tube) amplifiers, the current is usually manageable, but a centre tapped (i.e. positive and negative) supply isn't required. It is a simple matter to change the earth reference from the capacitor centre tap to the negative end of the supply as shown in Figure 8, so you end up with a 54V supply from a 25V transformer winding. With a high voltage doubler, the half voltage tap (between the two caps) is useful for supplying screen grids of output valves, and for the preamp stages. Note that the high voltage tap now has 100Hz ripple, and the half voltage tap has 50Hz ripple (120Hz and 60Hz respectively for 60Hz mains). Naturally, for valve equipment the voltages will generally be closer to 500V and 250V than shown above. The lower frequency ripple voltage from the mid point means better filtering is needed, which is a nuisance.
Interestingly, this type of supply is (or was up until fairly recently) fairly common with computer power supplies and the like. When used at 120V, the voltage switch on the back of the supply converted it from a bridge rectifier to a voltage doubler, and the SMPS circuitry works from a 300-340V DC supply as a matter of course. At that voltage, current is typically fairly low (around 500mA for a 150W supply). In use in this manner, it is mandatory that some form of inrush current limiting is used, because the mains has such a low impedance that diode or capacitor failure is almost guaranteed with possible inrush currents of hundreds of amps.
In all power supply designs where the power is significant, the transformer temperature rise must be accounted for. Apart from the transformer radiating its heat to nearby components, any temperature rise will increase the copper losses, leading to reduced performance and even more heat. Use of a larger than required transformer will help considerably, but at the expense of capacitor ripple current. Fan cooling of the transformer can increase its rating quite dramatically if done properly.
Naturally, an increase in ripple current will cause the capacitors to become hotter, and as always, an increase in temperature causes increased losses and shortened component life expectancy.
For similar reasons, it is unwise to mount the filter capacitors anywhere near a significant heat source, such as large wirewound resistors, heatsinks or other heat generating components. Valve amplifiers are the natural enemy of electrolytic caps, due to the often elevated temperatures within the chassis. Some manufacturers have resorted to mounting the filter caps in a separate metal enclosure on the outside of the chassis (and reasonably well away from output valves) in an attempt to keep temperatures down.
Somewhat surprisingly, some amplifiers defy all expectations, and electrolytic capacitors will be found to be within specifications even after 50 years of operation. In other cases caps will fail far earlier than expected, and this can be due to a 'bad batch', faulty manufacture (one off) or just a shonky manufacturer or fakes! Yes, counterfeit capacitors have popped up in the market, and some are found to have a small (cheap) capacitor inside the can for a much higher specification component. If the price seems too good to be true, then it probably is.
The required capacitance for a given load current and ripple voltage is determined (approximately) by the formula [1]...
C = ( I L / ΔV) × k × 1,000 µF ... whereI L = Load current
ΔV = peak-peak ripple voltage
k = 6 for 120Hz or 7 for 100Hz ripple frequency
Since all my calculations above were done using 100Hz ripple frequency (50Hz mains), this can be checked easily, so ...
I L = 1.44, ripple = 2V p-p, therefore C = 5,040µF
It can safely be concluded that this formula is more than acceptable for our needs, any error being less than the tolerance of electrolytics anyway. The net result is that the required capacitance is about 3,500µF per amp, for a 2V peak to peak ripple (50Hz supply). The required capacitance will be less for 60Hz countries, at 3,000µF per amp - again for a 2V p-p ripple voltage. My recommendation (above) for a minimum of 2,000µF per amp DC is still quite valid, but allows for higher ripple voltage (3V P-P rather than 2V P-P). Note that the formula and my 'quick and dirty' estimation are only approximations, and you will almost certainly see variations in real life.
I have seen it advocated that 100,000µF is the minimum that should be used with a powerful amp (say 200W / channel or so), but I find this difficult to justify. The law of diminishing returns comes into play quite quickly, and with both capacitance and transformer VA rating, this law becomes significant once you have doubled each of these values. With Class-AB amps, a ripple voltage of 2V P-P at full power will do nothing more than reduce the power by a few watts at the onset of clipping. Even reducing the capacitance further to (say) 1,500µF per amp will only reduce the continuous power output by a small amount. Normal music signals with their dynamic range will allow an amp with a relatively small capacitance to still provide the same maximum power for short transients.
As an example, a 100W/ 8 Ohm power amp will have a maximum output current of about 3.5A RMS into a resistive load. Since we know that a loudspeaker is not resistive, this figure can be doubled, to 7A. In fact, the inductive load of a loudspeaker will reduce the current delivered to the load and provided by the power supply, but let's not allow reality to cloud the issue  .
.
So, we'll allow for double the current to allow for ... something. This is not an absolute rule - you can multiply by three if that makes you any happier. The supply current for each supply (+ve and -ve) will therefore have a peak value of about 10A (7 × 1.414), and the average will be 1/2 of the speaker current, or 3.5A. Based on the 3,500µF / amp figure above (assuming a 50Hz supply), 12,250µF per side is enough to ensure that ripple voltage never exceeds 2V P-P, but since this is a non-standard value, we would use 10,000µF.
In reality, it is probably going to be quite OK with 4,700µF, and the loss of power is negligible in real terms. As stated above, continuous power will be reduced, but normal music signals will not have transients of sufficient duration to discharge the filter caps appreciably. Note that this does not apply to amplifiers that are used for sub-woofers, nor for Class-A amps. These will place a greater load on the supply, and on a more consistent basis.
If we were to increase the capacitance to infinity (big cap!), the ripple voltage will be 0V, and we will get an extra volt (peak) from the amp before the onset of clipping with a continuous signal. However, the cap will also take an infinite amount of time to charge, so you won't be able to use the amplifier at all for many years after it's turned on. After an infinite time when the cap has charged, you'll get about 4W increase, which is completely insignificant.
With more realistic capacitor values the situation isn't much different, but at least they will reach full voltage in your lifetime. Now we must remember that the mains voltage can fall (or rise) by up to 10%, which represents a power drop of around 20W - the 100W amp will only be capable of 80W with 10% low mains. Considering that an amplifier should not be operated at or near clipping anyway, the difference is inconsequential. If an amplifier is intolerant of a normal amount of supply ripple (typically a couple of volts peak-to-peak), then it's a poor design and shouldn't be used.
Use of a small (e.g. 1µF) polyester, polycarbonate or polypropylene capacitor across the DC output is a common practice. Electrolytics all exhibit a small inductance, and this causes their impedance to rise at higher frequencies. This is dependent on the physical size (mainly the length) of the cap - bigger caps usually have greater inductance. Again, the use of a paralleled bank of small (1,000µF) electros will be better in this respect than a single large can type, and will also be easier to mount and cheaper. I have never found the necessity to add a bypass cap across the electros to maintain amp stability, but it cannot hurt. Some amplifiers will oscillate if the supply impedance is allowed to exceed some specific (low) impedance at high frequencies. Essentially it is a good idea, and in the greater scheme of things, is inexpensive. Should you choose not to include a film bypass, it is unlikely that anything 'bad' will happen - the impedance of the large electrolytic will usually remain much lower than that of the film cap at any frequency below 1MHz or so.
As a reality check, note that the leads to and from the filter cap will generally have far more inductance than the capacitor itself, and it is often these leads (as well as PCB traces) that dominate the 'self-resonant' frequency of a capacitor. If the leads are too long, then some amplifiers will oscillate. The proper place for film bypass capacitors is on the amplifier board itself - not directly in parallel with the filter capacitors. You can do both, but only the caps on the power amp board will have any useful effect. As a guide, the inductance of a straight piece of wire in free space is approximately 5-6nH (nano-Henrys) per centimetre, so if you have 100mm (10cm) of wire between the filter caps and the amplifier, you have added ~55nH of inductance in the supply leads. It isn't much, but can cause high speed semiconductors to oscillate in a feedback circuit.
A common rule-of-thumb for wire inductance is 1nH/ mm, but all such simple 'rules' are only very rough approximations. A wire's inductance depends on its diameter as well as length, and is reduced by twisting wires (e.g. +ve and -ve) together. All wiring adds resistance as well, and this can cause more problems than the inductance.
You will often see graphs showing the self-resonant frequency of electrolytic capacitors, and they may start to show a rising impedance within the audio band. Very large capacitors will be 'worse' in this respect than smaller ones. This is part of the 'rationale' for using one or more smaller caps in parallel. Such graphs are misleading unless interpreted correctly, and can usually be ignored. The reason that the self-resonant frequency is so low has little to do with inductance, it's because the capacitance is so large! The impedance of the cap remains very low up to at least 100kHz, and is usually fine up to 200kHz or more. Feel free to test this for yourself.
Consider a 4,700µF cap with a series inductance of 100nH - two leads, each a bit less than 100mm in length. The standard formula ( Z = 1 / 2π √ L C ) tells us that the resonant frequency is only 7.34kHz. Surprisingly, it doesn't matter a great deal, because the impedance at 100kHz is only 62mΩ (62 milli-ohm) - ignoring ESR of perhaps 50mΩ or so (actual impedance at 100kHz will be around 80mΩ with 50mΩ ESR). Any small cap placed in parallel will have a much higher impedance. For example a 1µF cap doesn't get down to 80mΩ until you get to about 2MHz - and that assumes zero lead length and zero ESR. Despite claims to the contrary, the 'sound' of the DC is unchanged.
Note that wiring to the amplifier (or other load) must be taken from the filter capacitor's terminals, never from the rectifier. There is already a limit to the HF bypassing because of the electro's ESR, and any resistance you add only makes matters worse. The small resistance (and inductance) between the diodes and the filter capacitor can cause more high frequency energy to be superimposed onto the DC. There's a good chance that this will be audible with some designs. In case you are wondering, adding a 100nF film cap makes virtually zero difference in real terms. A reduction of 2.6µV is not significant compared to 65mV ripple - that's what I measured in a simulation, and assumes an ideal 100nF cap with zero lead inductance and resistance. A real-world component will show a great deal less difference.

Some designers include a bleeder resistor in parallel with the filter cap(s). Once an amplifier is working normally, this is redundant, and does nothing useful other than dissipate power. It can be very useful during testing though, as the caps can retain a charge for some time if the amp is not connected, leading to sparks and possible damage (uncommon, but it can happen). There are no rules for the value, but it wouldn't be sensible to use a 1Meg resistor in parallel with a 10,000µF capacitor, nor would it be sensible to use a 1 ohm resistor. In general, a resistor value that will discharge the caps to around 37% of the full voltage in around 10 seconds is reasonable, so for a 10,000µF cap that means a 1k resistor. If the supply voltage is ±56V, you'll need 5W resistors that will dissipate a little over 3W each. Work out the value and power rating needed for your application.
The manufacturers' ripple current rating is the maximum continuous ripple if the quoted life expectancy of the capacitor is to be achieved (usually 2000 hours, but 12000 to 26000 hours for some manufacturers). The ripple current rating is determined in part by the ESR (equivalent series resistance) and the maximum rated operating temperature (typically 85°C, but higher for high temperature types). The maximum ripple current can be increased by up to 2.5 times as the operating temperature is reduced (2.5 times at 30°C), though going above about 1.5 times is risky because the ESR increases as the capacitor ages and causes more heat for the same ripple current. [3]. Personally, I prefer not to exceed the quoted ripple current rating.
Capacitors in power supplies feeding Class-A amps should be operated well within their ripple current rating. In a Class-AB amp, the maximum ripple is at maximum output which only occurs occasionally (if at all!). Occasional excursions up to or even above the maximum ripple current will not significantly affect the life of the capacitor. In a Class-A amp however, the ripple is at or close to the maximum whenever the amp is switched on. If the ripple current is at the maximum for the capacitor, the life expectancy would be 2000 hours (for the normal types). This equates to a life of less than 2 years if the amp is used for 3 hours a day. It may last much longer, but that would be good luck rather than good management.
A formula for calculating ripple current would be very useful, but unfortunately (despite claims made in some articles I have read), it is almost entirely dependent on the series resistance provided by the incoming mains, the power transformer and rectifier diodes. Any formulae that do exist are only true for 'sub-optimal' values of capacitance (in other words, the cap is too small to be fully effective). The summary (below) has some guidelines that may be useful, but be aware that these are guidelines only - the final outcome has so many variables that it is impossible to give an accurate prediction of capacitor ripple current.
Remember that large capacitor values will have a smaller surface area per unit capacitance than smaller ones, so the use of multiple small caps instead of a single large component can be beneficial. There is more surface area, the ESR will be lower, ripple current rating higher, and the combination will most often be cheaper as well. This is an 'all win' situation - rarely achieved in any form of engineering. An example is worth showing - the following details are from an Australian electronics retailer's catalogue:
| Value (µF) | Voltage | Size (mm) Dia x H | Surface Area (mm²) | Ripple Current (mA) | Price (AU$) |
| 1,000 | 63 | 16 x 32 | 1659 | 1,400 | 1.95 |
| 2,200 | 50 | 16 x 35 | 1810 | 1,900 | 2.85 |
| 4,000 | 75 | 30 x 80 | 7634 | 4,600 | 14.50 |
| 8,000 | 80 | 35 x 76 | 8467 | 3,460 | 18.95 |
| 10,000 | 100 | 51 x 85 | 13779 | 8,100 | 32.95 |
For the sake of the exercise, we will assume that we need 8,000µF at a minimum of 50V, and with a ripple current rating of 7A - this is more than adequate for a 100W amp, and meets all the design criteria.
I shall leave it to you to do your own comparisons, but most of the time you will get similar results. This is a very good way to reduce the size requirements as well - it is far easier to fit a number of small caps into an enclosure than a couple of large ones, and since there is an overall improvement in specs as well as a price advantage, it is an elegant solution.
Note that the prices shown were obtained when this section was written (~2003) and will no longer be accurate. However, the trends described don't change, and remain representative regardless of component price variations.
It is worth pointing out that historically, filter capacitors are the number one cause of power supply failure. This is almost always because of the effects of temperature and ripple current, and close attention to this is very much worth your while. ESR is the best way to determine if a capacitor is still good or is on its last legs. An ESR meter is an excellent investment for anyone building or repairing amplifiers. When a cap goes 'bad', the ESR will rise to an unacceptable value even though the capacitance may seem to be within normal tolerance.
While inductance is not affected by the dielectric material, ESR is - it is dependent on the dissipation factor (DF) of the insulation material, as well as the resistance of the leads, plate material/ metallisation layers and plate terminations. Because DF varies with frequency and/or temperature in most common dielectrics, so too does ESR. While ESR is rarely a problem in most audio circuits, it's a different matter with power supplies. ESR (like all resistance) creates heat when current is passed, so for high current circuits the ESR is often a limiting factor.
ESR is very difficult to measure with low value capacitors, because the capacitive reactance is usually a great deal higher than the ESR itself. In general, it is safe to ignore ESR in most electrolytic and film caps used in signal level applications (such as electronic crossovers, coupling capacitors and opamp bypass applications). ESR becomes very important in high current power supplies, switching regulators/supplies and Class-D amplifiers, many digital circuits and any other application that demands high instantaneous currents that are supplied by the capacitor.
The table below shows the worst case ESR for new (standard, not low ESR) electrolytics for a range of capacitor values and voltages. If any cap with the value/ voltage shown has a measured ESR significantly exceeding that in the table, it is on the way out and should be replaced. The table was compiled using the details printed on my ESR meters, and is representative - some new caps will be much better than shown, some may not be quite as good, and ultimately you need to use your own judgement as to whether the measured ESR will cause a problem or not.
Some people have wondered why ESR is usually tested at 100kHz. The reason is simple - at that frequency, the capacitive reactance of a 1µF cap is only 1.6 ohms, and any 'resistance' measured is therefore predominantly the ESR of the capacitor. This is why it's rather pointless to try to measure the ESR of any capacitor below 1µF - it can be done, but the measurement frequency must be much higher than 100kHz. Larger values have much less reactance, and the capacitive reactance is negligible.
| Capacitance | Voltage | ||||||
| 10 | 16 | 25 | 35 | 63 | 160 | 250 | |
| 1µF | 14 | 16 | 18 | 20 | |||
| 2.2µF | 6.0 | 8.0 | 10 | 10 | 18 | ||
| 4.7µF | 15 | 7.5 | 4.2 | 2.3 | 5.0 | ||
| 10µF | 8.0 | 5.3 | 3.2 | 2.4 | 3.0 | 2.5 | |
| 22µF | 5.4 | 3.6 | 2.1 | 1.5 | 1.5 | 1.5 | 1.8 |
| 47µF | 2.2 | 1.6 | 1.2 | 680m | 560m | 700m | 800m |
| 100µF | 1.2 | 700m | 320m | 320m | 300m | 150m | 800m |
| 220µF | 600m | 330m | 230m | 170m | 160m | 90m | 500m |
| 470µF | 240m | 180m | 120m | 90m | 90m | 50m | 300m |
| 1,000µF | 120m | 90m | 80m | 70m | 50m | 60m | |
| 4,700µF | 120m | 85m | 70m | 60m | 40m | ||
| 10,000µF | 120m | 80m | 60m | 40m | 30m | ||
The above table is approximate, and gives worst case ESR figures for various capacitors at different rated voltages. ESR is normally measured at 100kHz, where the capacitive reactance is low enough that it doesn't affect the reading. ESR is also affected by the dissipation factor (DF) of the electrolyte and the internal construction of the capacitor. Caps that are (or claim to be) low ESR use different formulations for the electrolyte to obtain the lowest ESR practical. Note that ESL (equivalent series inductance) is generally very small, and is often almost entirely the result of leads that are too long.
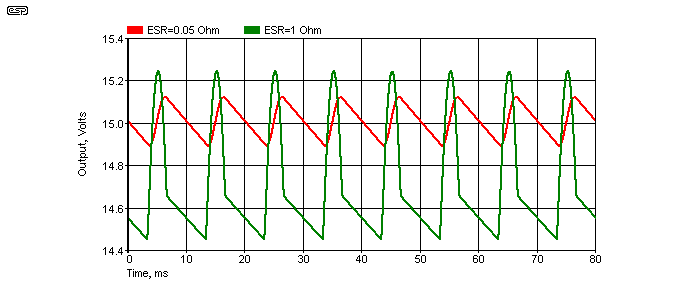
Figure 9 - Ripple Voltage, Normal And High ESR Capacitor
Capacitors can develop a high ESR as a result of age, being placed adjacent to hot surfaces, excessive ripple current or even faulty manufacture. When a main filter capacitor in an amplifier's power supply develops a high ESR, the effect can usually be seen on the ripple voltage waveform. The above is exaggerated for clarity, but shows the waveform with a normal 4,700µF capacitor with an ESR of around 50mΩ compared to another where the ESR has risen to 1 ohm. The output current is about 150mA, and the spikes on the leading edge of the green waveform indicate immediately that the capacitor is faulty.
Should you simply measure capacitance with a suitable meter, it will often show a reading that's well within the normal range. The ESR increases well before the capacitor loses significant capacitance, and that's why it's important to verify that the ESR is alright. In most cases, this can be measured with the capacitor in situ, but make sure it is fully discharged to prevent damage to the ESR meter. This is often one of the first tests conducted on switchmode supplies, because high ESR can cause them to malfunction (usually unpredictably).
Should you happen to measure a waveform similar to the green trace with new capacitors, it could be because the measured voltage is taken from the bridge rectifier rather than the filter capacitors. It probably won't be as bad as that shown, but the supplies to an amplifier or regulator must always be taken directly from the filter cap terminals, and never from the rectifier. Even a small resistance can introduce considerable noise (usually 'buzz') into the audio. It might not look like it, but the green waveform has greatly increased high frequency noise compared to the red trace.
One thing I strongly recommend for power amplifier power supplies is the use of 35A chassis mounted bridge rectifiers. Because of the size of the diode junctions, these exhibit a lower forward voltage drop than smaller diodes, and they are much easier to keep cool since they will be mounted to the chassis which acts as a heatsink. As always, lower temperatures mean longer life, and as was demonstrated above, the peak currents are quite high, so the use of a bigger than normal rectifier does no harm at all.
Even given the above, I have had to replace bridge rectifiers on a number of occasions - like any other component, they can (and do) fail. The bigger transformers increase the risk of failure, due to the enormous current that flows at power-on, since the capacitors are completely discharged and act as a momentary short circuit. You must always consider the peak current, which as shown above is much higher than the RMS or average value. With a 'typical' power supply, the peak diode current can exceed five times the DC current, even though the average diode current will be about half the DC current. Diodes are (almost) always specified for average current, with a repetitive peak current capability that can handle the expected peak current in normal use.
Diodes used in a FWCT (Full Wave Centre Tapped) or single Full Wave supply rectifier must be rated at a minimum of double the worst case peak AC voltage. So for example, a 25V RMS transformer will have a peak AC voltage of 35V when loaded, but may be as high as 40V unloaded, and double this is 80V. 100V Peak Inverse Voltage (PIV) diodes would be the minimum acceptable for this application.
Voltage doubler supplies are very uncommon for transistor power amps, but are sometimes used for preamp supplies and valve (vacuum tube) amplifiers. The diode PIV must be at least double the peak AC voltage, so (for example) with a 200V winding (282V peak) the diodes need to be rated for a minimum of 600V.
For a single bridge rectifier, PIV only needs to be greater than the peak AC voltage, since there are effectively two diodes in series. In the case of a dual supply (using a 25-0-25V transformer), the worst case peak AC voltage is 80V, but using diodes rated for 200V PIV is wise. The most common 35A chassis mounted bridge rectifiers are rated at 400V, and this is sufficient for all supplies commonly used for power amplifiers of any normal (i.e. < 500W into 8 ohms). Beyond this, the voltage rating is fine, but the current rating is inadequate, and a higher current bridge should be used. Alternatively, use a separate bridge and filter capacitors for each channel.
There is currently a trend towards using fast recovery diodes in power supplies, since these supposedly sound 'better'. There is absolutely no requirement for them, but they do no harm. The purpose of a fast recovery (or any other fast diode) is to be able to switch off quickly when the voltage across the diode is reversed. All diodes will tend to remain in a conducting state for a brief period when they are suddenly reverse biased. This is extremely important for switchmode supplies, since they operate at high frequency and have a squarewave input. Standard diodes will fail in seconds with the reverse current, since it causes a huge power loss in the diode.
At 50 or 60Hz, and with a sinewave input, the slowest diodes in the universe are still faster than they need to be. Despite this, high speed diodes actually do cause less 'disturbance' at the transformer's secondary. Not that it makes the slightest difference to the DC. Nelson Pass suggests that even the standard diodes should be slowed down with paralleled capacitors [2]. This might help, as it reduces the radiated and conducted harmonics from the diode switching. These switching harmonics can extend to several MHz, even with the normal 50/60Hz mains.
Typically, capacitors between 10 and 100nF (optionally with a small series resistance) are wired in parallel with each diode in the bridge, and this is quite common with some high end equipment and test gear where minimum radiated noise is essential. Some constructors like to add snubbers (a series resistor and capacitor) in parallel with the transformer secondaries. For more info on that topic, see Power Supply Snubbers which covers this in detail. Don't expect a snubber or fast diodes to change the DC, because they won't (and this has been tested and verified on the workbench). The main filter capacitors have a very low impedance at all frequencies of interest, and they effectively remove all traces of switching transients (they are not particularly fast, despite 'alternative' opinions).
For reasons that I find completely obscure, there are some who claim that there are audible differences between power supply filter caps, diodes and mains leads. The net result of all the transforming, rectifying and filtering described above, is to produce DC. OK, it is not pure DC, in that it has some superimposed AC, as ripple voltage. Very few power amplifiers are so intolerant of ripple or other signals on their supply lines that a couple of volts will be audible. If this is the case, then a regulated supply, or at least a capacitance multiplier, is essential.
Very small amounts of noise that manage to get through the supply also should have no effect on an amp, and if the amp is so afflicted, the remedy is the same as for ripple. Remember that at all audio frequencies, the reactance of the capacitor is very low, and will act as a short circuit for any stray noise signals. A 10,000µF cap has a theoretical reactance (impedance) of 1.6 milliohms at 10kHz. This will never be achieved in practice - the wire has more resistance than that and even seemingly short lengths of wire add inductance. Suffice to say that the impedance is pretty low, and it is extremely hard for any appreciable signal to get past the filter capacitors. The addition of one or more 1µF film type bypass caps ensures that impedance stays low even at radio frequencies, but as noted earlier, beware of long leads!
The above assumes that the problem is noise, but this is rarely stated as the 'improvement' - it is more likely to be bass 'authority' or extension, or perhaps the 'veil' is lifted from the highs. It can readily be demonstrated that as long as a power supply is well engineered in the first place, the 'quality' of the DC output is unaffected by any of the so-called 'remedies'. Ripple voltage will remain the same, amplifier power output (at all frequencies) will be unchanged, and mostly the signal to noise ratio will be unaffected. It is very easy to monitor the supply rails with an oscilloscope and a monitor loudspeaker (capacitively coupled of course), and from this it is possible to directly assess any difference should it exist.
Always beware of any purely subjective claim that this or that will 'improve' a circuit, an amplifier or anything else. Without technical backup, test results and measurements, these claims are almost invariably bogus. Double-blind (or ABX) testing is the only subjective test methodology that can be believed.
I have yet to hear from anyone who can give a plausible explanation or send me test results or a sound file that demonstrates the difference between any two mains leads or even two 'equivalent' power supplies, all else being equal. This is snake-oil and should be avoided. In a (very) few cases, the use of a mains lead that has an outer shield might reduce noise, but it can have little effect on anything else.
Another 'interesting' myth is that using a snubber (essentially a Zobel network consisting of a series resistor and capacitor) across the diodes or transformer secondary windings will "improve the sound". It won't do anything of the sort, but in some cases may reduce conducted EMI (electro-magnetic interference conducted back to the mains via the power lead) if this happens to be a problem. This is covered in detail in the article Snubbers For Power Supplies - Are They Necessary And Why Might I Need One?. As with many of the other mythical/ magic 'ingredients' that can be added to power supplies, they won't hurt anything, but they also will not change the 'sound' of the DC. By all means include snubbers if it makes you feel better, but don't go posting nonsense on-line about the "amazing difference" they make. It doesn't happen unless your internal wiring is poorly laid out and you get buzz as a result of internal radiated magnetic fields.
In conclusion, there are some rules of thumb that can be applied to save calculations and test measurements. These should not be considered as gospel - they are merely my suggestions on acceptable minimum requirements for a power supply. Adding snubbers, high speed diodes or film caps in parallel with the main filter caps does no harm, but it doesn't improve anything, with the possible exception of a small decrease in conducted emissions (RF energy fed back into the mains supply).
Diode Ratings
Larger transformers (i.e. higher VA rating) usually have lower losses (watts per VA) at full (or average) power. This is because they need fewer turns of heavier gauge wire with a larger core. That means that the DC voltage will be higher than for an otherwise similar transformer of lower rating. For example, the DC output from a 25-0-25V 500VA transformer will significantly higher than that from a 25-0-25V 100VA transformer at the same DC load current. This is particularly important for Class-A amplifiers, because they draw considerable current 100% of the time.
Because the regulation of small transformers is worse than for large ones, you may find that the no-load DC voltage is higher than expected, and the full-load voltage lower. This is normal, and it happens with all transformers. It varies depending on the size of the transformer. A large transformer will nearly always provide a DC voltage that has better regulation than you can get from a small transformer with the same AC voltage output.
You can increase the VA rating of any given transformer by using fan cooling. The increase depends on the surface area of the transformer that is subjected to turbulent airflow. Laminar or 'smooth' airflow is comparatively ineffective, because it allows a layer of still air to exist next to the transformer. Fans must blow air onto the transformer, and not suck air past it - the difference can be considerable. You will need to experiment if you want to run a transformer beyond its ratings, and be aware that you only increase the VA rating, and regulation will be worse than a larger transformer.
Since the power supply is connected to the mains, it is necessary to protect the building wiring and the equipment from any major failure that may occur. To this end, fuses are the most common form of protection, and if properly sized will generally prevent catastrophic damage should a component fail.
Toroidal transformers have a very high 'inrush' current at power-on, and slow-blow fuses are essential to prevent nuisance blowing. In the case of any toroid of 500VA or more, a slow-start circuit is very useful to ensure that the initial currents are limited to a safe value. An example of such a circuit is presented in Project 39, and represents excellent insurance against surge damage to rectifiers and capacitors.
Calculating the correct value for a mains fuse is not easy, since there are many variables, but a few basic rules may help. Firstly, check the manufacturer's data sheet or website. Often they will have recommended fuse ratings and types to suit their transformers in use. If manufacturer data is unavailable, determine the maximum operating current of the system, based on continuous maximum power. The calculations done previously will help.
The mains current is determined by the turns ratio of the transformer, calculated by ...
Tr = Vpri / Vsec Where Tr is turns ratio, Vpri is primary (mains) voltage, and Vsec is secondary voltage
A 240V to 25-0-25V (i.e. a 50V secondary - the whole secondary winding must be used in the calculations) transformer has a turns ratio of 4.8:1, the same transformer with a 120V primary has a turns ratio of 2.4:1 - this can be calculated for any transformer. The primary current is calculated by ...
Ipri = Isec / Tr Where Ipri is primary current, Isec is secondary current
A supply designed for our hypothetical 100W/ 8 ohm amplifier will have a secondary current of about 6.3A at full power, so primary current (for 240V) is about 1.3A. A 2A fuse would seem OK for this, but if a 500VA transformer was used (for example), this is enough to handle the maximum transformer primary current, but will (eventually) blow due to the transformer's inrush current. A 3A (or 3.15A) slow-blow fuse should be used, and this should survive the inrush current (120V countries will need a 6A slow-blow fuse). I recommend the use of a soft-start circuit for any transformer above 300VA.
Thermal protection (often by way of a once-only thermal fuse) is often included in transformers. Generally (but not always) this is limited to small transformers that have a fine gauge primary winding, and they often draw perhaps twice their normal primary current, even when the output is shorted!. A normal fuse can withstand that small overload for long enough to enable a complete melt-down! If the 'one-time' thermal fuse has been used, should the transformer overheat it must be discarded, since the fuse is buried inside the windings and cannot be replaced. All the more reason to ensure that the transformer is properly protected at the outset. Feel free to add your own thermal fuse, but make sure it is in good thermal contact with the windings, is well away from any airflow (intended or otherwise) and that the wiring to it is safe under all possible conditions. This isn't trivial, but it does add an extra level of protection - but only if done properly.
Multi-tapped primaries (e.g. 120, 220, 240V) create additional problems with fusing, and often a compromise value will be used. The transformer protection is then not as good as it could be, but will generally still provide protection against shorted diodes or filter caps. Ideally, there will be different fuse ratings for 120 or 230V operation, and the correct fuse should always be used.
Additionally, it can be an advantage to fit Metal Oxide Varistors (MOVs) to the mains - between the active and neutral leads. These will absorb any spikes on the mains, and may help to prevent clicks and pops coming through the amplifier. MOV specifications can be daunting though, and it will often help if you ask the supplier for assistance to pick the right one for your application. They usually can only withstand a limited number of over-voltage 'events' before they fail completely, and the normal failure mode is for them to explode (and no, I'm not joking).

Note that primary fuse or circuit breaker protection does not protect the amplifier against overload or shorted speaker leads. If this happens, or should the amplifier fail, the primary fuse offers no protection against catastrophic failure, speaker damage and possibly fire. For this reason, secondary DC fuses should always be used - no exceptions. Many people also like to include DC protection, such as Project 33. Many commercial and kit versions fail to show the correct relay contact wiring, and they may be next to useless.
Inrush current is defined as the initial current drawn when the power is first applied. With transformer based power supplies, there are two separate components - transformer inrush and capacitor charging current. They are very much interdependent, but the maximum current at power-on cannot exceed a value determined by the transformer's primary resistance. The optimum part of the waveform to apply power for a transformer is at the peak of the AC voltage - 325V for 230V mains. See Transformers, Part 2 for more info.
To minimise capacitor inrush, power should be applied at the mains zero crossing, where the maximum rate of change of voltage is the lowest. When a switch is closed, the rate of change is extremely high if there is appreciable voltage across the switch contacts at the time.
These two are completely at odds with each other, but the exact moment when power is actually applied is effectively random. In addition, there is the effect of the (discharged) capacitor applying an instantaneous heavy overload to the transformer at power-on. This will tend to reduce the transformer's flux density, but the cap(s) will behave as a momentary short-circuit (via the diode bridge), so the only way to know what really happens is to run tests. This level of testing is not trivial and requires specialised test equipment, but fortunately is not really necessary.
With transformers of 300VA or less, you usually don't need to do anything at all. If the correct rating and type of fuse is used, the inrush current will be high but well within 'normal' range. The worst case inrush current can be no more than around 50A (at 230V for a 300VA transformer), because it's limited by the primary resistance and mains impedance. Duration is typically less than one AC cycle. Larger transformers create higher inrush current because the primary resistance is lower. The capacitors have to charge, and as noted above (see Table 6) the capacitor inrush duration is much less than 500ms, even with extremely large capacitors.
The easiest way to limit the inrush is to use a soft start circuit such as Project 39. Using NTC thermistors alone is a poor choice, because most amplifiers don't draw enough current at idle to obtain a low series resistance. The thermistor resistance will be constantly cycling when the amp is driven with a signal, and there is little protection if the amp is (accidentally or otherwise) switched off and back on again quickly.
A soft start circuit protects the fuse from very high surge currents, limits the capacitor charging current, and makes the power-on cycle much more friendly to the equipment and the incoming mains. The resistors (or thermistors) should be selected so that the maximum peak current is between 2 and 5 times the normal full power operating current. For example, if an amplifier is expected to draw 2A at maximum power, the soft start should limit the worst case peak current to somewhere between 4 and 10 amps. For 230V mains, the resistance will be between 23 and 58 ohms. The standard values I suggest for Project 39 are around 50 ohms for 230V (or 22 ohms for 120V), and these have proven to be effective and reliable for many hundreds of constructors.
Provision of a soft start is also needed for most switchmode power supplies. Unlike a linear supply, there is no transformer primary winding resistance to limit the current, and the low ESR of the capacitors can cause exceptionally high inrush. I've measured the inrush of a fairly modest SMPS (150W) at 80A peak, and even a small 20W SMPS can cause 10A or more peak inrush current. Many of the latest generation of switchmode supplies use an active soft start circuit because the inrush current often causes circuit breakers to trip if several supplies are turned on at the same time. A modest 150µF/ 400V electrolytic capacitor will have a typical ESR of no more than 2 ohms, so if not limited, inrush current can be 150A or more - at least in theory.
In practice, there are several additional impedances that help mitigate the inrush current. Mains wiring (including plugs and sockets), diodes, fuses and PCB tracks all contribute some resistance and that keeps the inrush current below 100A in most cases. To ensure that inrush never causes a problem, a soft-start circuit has to be used.
EMI is not usually a problem with a linear power supply, and most will pass the regulations used in all countries without any filtering. However, it's quite common to use at least some kind of filter, which in many cases will be nothing more than a capacitor. There are three possible approaches, with none being significantly better or worse than another. There can be a large cost difference though, and it's up to the constructor to decide which approach is used.
The first method is to use a mains rated (Class X2) capacitor in parallel with the transformer's primary. It's important to understand that no standard capacitor can be used - it must be an X2 mains cap. This is doubly important for mains voltages of 220-240V, because all DC rated caps will eventually fail, regardless of the voltage rating. X2 caps are specifically designed for use across the mains, and are usually (but not invariably) polypropylene. A common voltage rating is 275V AC, which is ideal. A capacitance of around 470nF is generally suitable.
The second is to use a capacitor across each winding of the transformer's secondaries. Again, I suggest that you use Class-X2 caps, especially for secondaries of more than 50V AC. The task gets harder for valve amps, because the secondary voltage is usually in the range of 300V to 600V AC, so a series string of caps will almost certainly be needed. When a series string is used, it's a good idea to include resistors in parallel with each cap to ensure the voltage across each is equal. Be careful with the resistors - it will often be necessary to use several in series so the voltage across each is limited to a safe value. Using resistors with a high voltage across them will almost always lead to eventual failure!
The third method is common when people decide that fast diodes sound 'better', and they add a cap in parallel with each diode to slow it down again (that has to be pointless). The same can be done with standard diodes. This isn't a method I've used, but I'd expect it to be similar to using a single cap (or two caps for a dual winding) across the transformer secondary winding(s).
None of the above will make much (if any) difference to the harmonics generated within the audio band, but they can help reduce radio frequency noise by a few dB. The test used to determine whether there's a benefit or not is 'conducted emissions' - noise and/or interference that's passed back into the mains wiring through the mains lead itself. In most cases, it's highly unlikely that you will hear any difference, unless the added cap manages to reduce audible noise (improbable in a well laid out system).
For more info on the topic, see the article Power Supply Snubber Circuits. While not essential (and it doesn't affect the sound), adding snubbers to the transformer secondary (or secondaries) can reduce EMI to a worthwhile degree. While EMI is rarely bad enough to prevent any transformer supply from passing conducted emissions tests, a snubber can provide an extra 'safety margin'. Far worse is the level of harmonic distortion (and poor power factor) caused by the very non-linear waveform.
For many applications, the power supply of choice has now become one of the many different switchmode types. Some larger SMPS have active power factor correction to minimise the mains current when heavily loaded. I will only look at the basic principles here, because SMPS design is a complete career in itself. Any attempt to try to explain the finer points is futile because this is just one page of my site. Entire sites are devoted to SMPS design, and the design is non-trivial in every respect. There is an article on the ESP site that covers the basics though - see SMPS Primer for the details.
Manufacturers use a SMPS because it is much smaller than an equivalent linear supply, and as noted can include active power factor correction (PFC). This is designed to keep the mains waveform as close to the mains voltage waveform as possible. This minimises current for the same power, and reduces mains distortion (which is becoming a major problem). More importantly, a SMPS will often be cheaper than a traditional power supply, and of course is a great deal lighter.
Figure 10 - SMPS Block Diagram
The PFC circuitry uses raw (unsmoothed) rectified AC, so it has a very high ripple component (325V P-P for 230V input). The ICs are specifically designed to be able to deal with this waveform, and the output of the PFC circuit is DC - usually at around 350 - 420V. Most active PFC controllers provide a well regulated output voltage. If the active PFC stage is not used, the PFC block above is replaced with a conventional rectifier and high voltage filter capacitor(s). The PWM switching circuit is then responsible for all regulation (if used - many SMPS used for amplifiers do not provide regulation). (As noted above, many of the latest generation of SMPS use an active soft start circuit to limit inrush current.)
The DC is then chopped at high speed (typically 50kHz or more) into a pulse width modulated (PWM) signal for regulated supplies, or a simple squarewave signal. This allows the transformer to be very small even for high power systems, due to the high operating frequency. The output of the transformer is rectified and filtered, and the filter caps can be quite small because the input is a rectified high frequency squarewave. The DC then goes to the (sometimes optional) monitoring circuitry. This may be designed to provide tightly regulated supplies, and/ or to monitor the output current for fault conditions, etc. It's not at all uncommon for SMPS to use an internal low-power SMPS to provide normal working voltages for the IC(s) and 'housekeeping' circuitry.
The overall circuitry may initially appear simple if you look at the printed board for such a supply, but then you realise that it's almost always completely surface mount devices (SMD), with tiny components on both sides of the PCB. The overall complexity is often astonishing, and the possibility of servicing these supplies ranges from dubious to not-a-chance. It might be possible if you have full schematics and a manufacturer supplied test procedure (along with full SMD rework facilities), but in many cases the only option is to replace the PCB.
It's not at all uncommon for the PCB to be burned when a SMPS fails, because the protection circuits can only function if the circuitry is functional. There are countless failure modes that defeat all attempts at protection. Electrolytic capacitors are often the Achilles heel of any SMPS, and it's very common for them to develop a high ESR after a few years. In some designs, a single high ESR capacitor can cause the switching circuitry to fail - often spectacularly.
SMPS are used because people want gear that's light, powerful and cool running. Manufacturers like them because they are fairly cheap to make, and shipping and handling costs are reduced because of the low weight. No more bulky transformers and large capacitor banks. Few purchasers understand the downsides though.
The expected life of a conventional linear supply is close to infinite. There are few parts, all are easily procured (even custom transformers aren't overly expensive) and service is a breeze. Any SMPS can be expected to last until it's first used, and with any luck it can last for quite a few years thereafter. Will you be able to repair it in 10, 20 or 30 years? In a word - "no". The power supply (and often the amplifier too) become electronic waste once the specialised ICs are no longer available. Some of these parts may have a single production run, and are never made again.
Whether I like the idea or not is beside the point - this is what's being made today, and customers have to put up with it. DIY people will be making linear supplies for quite some time yet though, and they will most likely still be repairable in 50 years time!
For those who want to know more about SMPS in general, there is some more info on the ESP site, and the OnSemi reference has some excellent introductory info (although the very latest developments are not included as it was published in 2002). There is another OnSemi document that explains power factor correction, as well as countless others from various manufacturers.
The information presented in this article is intended as a guide only, and the author takes no responsibility for any damage, disfigurement or injury to persons (including but not limited to loss of life) or property that results from the use or misuse of the data or formulae presented herein. It is the readers' responsibility absolutely to assess the suitability of a design or any part thereof for the intended purpose, and to take all necessary precautions to ensure the safety of himself/ herself and others.
The reader is warned that the primary and secondary voltages present in nearly all power supplies for amplifiers are potentially lethal, and constructors must observe all applicable laws, statutory requirements and other restrictions or requirements that may exist where you live.
WARNING: All mains wiring should be performed by suitably qualified persons, and it may be an offence to perform such wiring unless so qualified. Severe penalties may apply.
All power supplies must be fused or protected by an approved circuit breaker, and all mains wiring must be suitably insulated and protected against accidental contact to the specifications and requirements that apply in your country.
The references cited here are those I used when compiling the article, but there are many others. Many books have been written on the topic, and there are countless websites that also have information. Whether it is reliable, useful or even factual is not always clear, so it's important to verify that what you read is relevant and/or based on science - as opposed to 'magic' or snake-oil. There are countless claims that do not stand up to scrutiny, so you have to be careful whenever you read articles on the Net. In general, avoid 'hints' and other material found in forum sites - these rarely agree with reality.
 Main Index
Main Index
 Articles Index
Articles Index