Active Filters

There is a wide range of filter circuits, each with its own set of advantages and disadvantages. All filters introduce phase shift, and (almost all) filters change the frequency response. There is one class of filter called 'all-pass' that does not affect the response, only phase. While at first look this might be thought rather pointless, like all circuits that have been developed over the years it often comes in very handy.

Filters also affect the transient response of the signal passing through, and extreme filters (high order types or filters with a high Q) can even cause ringing (a damped oscillation) at the filter's cutoff frequency. In some cases, this doesn't represent a problem if the ringing is outside the audio band, but can be an issue for filters used in crossover networks (for example).

If you are not already familiar with the concept of filters, it might be better to read the article Designing With Opamps - Part 2, as this gives a bit more background information but a lot less detail than shown here. There is some duplication - the original article was written some time ago, and it was considered worthwhile to include some of the basic info in both articles.

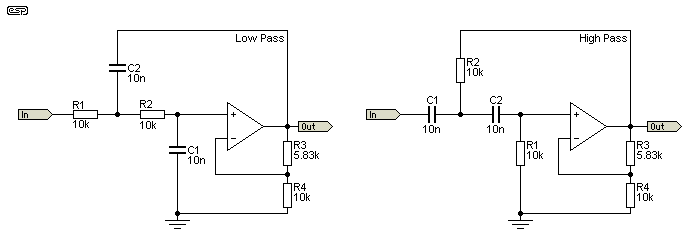
Filters are used at the frequencies where they are needed, so the filters described here need to be recalculated. I have normalised the frequency setting components to 10k for resistors, and 10nF for capacitors. This provides a -3dB frequency of 1.59kHz in most cases. Increasing capacitance or resistance reduces the cutoff frequency and vice versa.

Capacitors used in filter circuits should be polyester, Mylar, polypropylene, polystyrene or similar. NP0 (aka C0G) ceramics can be used for low values. Choose the capacitor dielectric depending on the expected use for the filter. Never use multilayer ceramic caps for filters, because they will introduce distortion and are usually highly voltage and temperature dependent. Likewise, if at all possible avoid electrolytic capacitors - including bipolar and especially tantalum types.

The following is actually a fairly small sample of all the different topologies, but the examples have been selected based on their potential usefulness. Some of the circuits shown are extremely common, others less so. In the general discussions about filter properties I have avoided heavy mathematical analysis. The maths formulas provided are enough to allow you to configure the filter - few readers will want to perform detailed calculations and they are not generally useful other than for university exams.

Within this article, the filters are intended for 'audio' frequencies, meaning only that they are not generally suitable for frequencies above ~100kHz or so. This limit is imposed by the opamps, not the filters as such. However, at radio frequencies (RF, above perhaps 200kHz or so), it's far more common to use inductors and capacitors, because the inductance required is small, and the parts are physically small too. While high speed circuitry can allow any of the filters to operate at RF, the cost will generally be far greater than for 'conventional' L/C filters. For opamp based active filters, there is no lower limit (other than DC), so operation at 0.1Hz or less is perfectly acceptable if that's what you need.

In the early days of electronics and still today for RF (radio frequency), filters used inductors, capacitors and (sometimes) resistors. Inductors for audio are generally a poor choice, as they are the most 'imperfect' of all electronic components. An LC (inductor/ capacitor) filter can be series or parallel, with the series connection having minimum impedance at resonance. The parallel connection provides maximum impedance at resonance. This article does not cover LC filters, but there are cases where the final filter uses an active equivalent to an inductor (a gyrator for example).

Gyrators are every bit as imperfect as 'real' inductors within the audio frequency range, but with the benefits that they are not affected by magnetic fields, and are smaller and (usually) much cheaper than a physical inductor. They are also very easy to make variable using a potentiometer, which allows functionality that may otherwise be difficult and/ or expensive to achieve. So, if you are looking for information covering the design and construction of passive LC filters, this is not the place to find it.

It's important to understand that all filters introduce phase shift, and there is no such thing as a filter without phase shift. Any two filters with the exact same frequency response will have the same phase response, regardless of how they are implemented. There are countless spurious claims from manufacturers (especially for equalisers) that this or that equaliser is 'better' than the competition's EQ because it has 'minimum phase' or 'complementary phase' (etc.). These claims are from marketing people, and have no validity in engineering. Contrary to what is often claimed, our ears are insensitive to (static) phase response, but we can detect even quite small variations in frequency response.

The common terminology of filters describes the pass-band and stop-band, and may refer to the transition-band, where the filter passes through the design frequency. Q is a measure of 'quality', but not in the normal sense. A high-Q filter is not inherently 'better' than a low-Q design, and may be much worse for many applications. In some cases, the term 'damping' is used instead, which is simply the inverse of Q (i.e. 1/Q).

It is generally defined that the -3dB frequency is the point where the output level has fallen by 3dB from the maximum level within the passband. This means that if a filter produces a 1dB peak before rolloff, the -3dB point is then actually 2dB below the average level. I tend to disagree that this is the most appropriate way to describe the filter's behaviour, but it is accepted as the 'standard', so I won't attempt to break with tradition here.

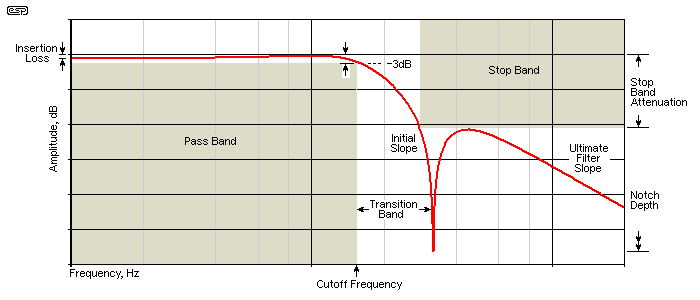
The above shows the major characteristics of a low pass filter. A high pass filter uses the same definitions, but obviously the stop band is at the low frequency end. Insertion loss is not common with active filters, but is always present with passive designs. The filter response shown is for a Cauer/ elliptical filter, only because it has all of the details needed to describe the various sections of the response. Passband ripple isn't shown (there's just a small peak before rolloff) because very few filters designed for audio show this behaviour. It's generally only found in multi-stage, fast rolloff filters.

Not all filters show all of the responses shown. Most 'simple' filters do not have a notch in the stop band, and the ultimate rolloff is usually reached about 2 octaves above or below the -3dB frequency. Most have no peak before rolloff either, but are simply smooth curves that roll off at the desired rate.

There are several different filter types, generally described by their behaviour. The basic types are low-pass, high-pass, bandpass, band-stop (notch) and all-pass. There are also many sub-types, where either a combination of filter types is incorporated into a single block, or different filters are combined to produce the desired result.

Then we need to describe the different topologies, some of which are named after their inventor/discoverer, while others are named based on their circuit function. For example the Linkwitz-Riley crossover filter set was invented by Siegfried Linkwitz and Russ Riley, the Sallen-Key filter was invented by Roy Sallen and Edwin L. Key (thanks to a reader, I discovered not only their first names, but also found that they invented a portable radar system called 'Chipmunk'), and the state-variable and multiple feedback filters are described by the functionality of the circuit. The biquad filter is known by the type of equation that describes its operation (the bi-quadratic equation). Wilhelm Cauer was the inventor of the Elliptical filter - also known as a Cauer filter.

Of all the filters, the Sallen-Key is the most common - it has excellent performance, is simple to implement, and it can have an easily varied Q by either changing the system gain (equal component value design), or component selection. Stop-band performance is generally good, with the theoretical attenuation extending to infinity (at an infinite frequency). 'Real world' implementations are not as good due to limitations in the active circuitry (whether opamps or discrete), but are more than acceptable for most applications. Other popular types are the multiple-feedback (MFB) filter, and (somewhat surprisingly) the all-pass filter.

Multiple feedback (MFB) filters are also popular, being easy to implement and low cost. Unfortunately, the formulae needed to calculate the component values are somewhat complex, making the design more difficult. In some cases, a seemingly benign filter may also require an opamp with extremely wide bandwidth or it will not work as expected. High-pass MFB filters cannot be recommended because of very high capacitive loading, which will stress most opamps and can cause instability and/or high distortion.

Less common (especially in DIY audio applications) are the rest of the major designs ...

Finally, there is a circuit that is quite common, but is not a filter in its own right. The simulated inductor uses an opamp to make a capacitor act like an inductor. Because there are no coils of wire, hum pickup is minimised, and cost is much lower than a real inductor. When used with a capacitor in series, it acts like an L-C tuned circuit. Very high 'inductance' is possible, but circuit Q is limited by an intrinsic resistance.

The generalised formula for first order filters is well known, and variants are used for higher orders. This depends on the topology of the filter, and for some the standard formula doesn't work at all. For reference ...

fo is the frequency, which is either the -3dB frequency for high and low pass filters, or the centre frequency for band pass types.

A bandpass filter's Q is defined as the centre frequency (fo) divided by the bandwidth (bw) at the -3dB frequencies. For example, if the centre frequency is 1kHz, the upper -3dB frequency is 1.66kHz and the lower -3dB frequency is 612Hz, the bandwidth is 1.05kHz. Therefore ...

High and low pass filters also have a Q figure, but it doesn't define the bandwidth. Instead, the Q determines what happens around the transition frequency. High Q filters usually have a peak just before rolloff, and low Q filters have a very gradual rolloff before reaching their ultimate slope (6dB/octave, 12dB/octave, etc.). Converting Q/ bandwidth to octaves can be somewhat tedious, but the following table should be helpful.

Q	BW (oct)	Q	BW (oct)	Q	BW (oct)
0.50	2.54	1.50	0.945	6.50	0.222
0.55	2.35	1.60	0.888	7.00	0.206
0.60	2.19	1.70	0.837	7.50	0.192
0.65	2.04	1.80	0.792	8.00	0.180
0.667	2.00	1.90	0.751	8.50	0.170
0.70	1.92	2.00	0.714	8.65	0.167
0.75	1.80	2.15	0.667	9.00	0.160
0.80	1.70	2.50	0.573	9.50	0.152
0.85	1.61	2.87	0.500 (½ Octave)	10.0	0.144
0.90	1.53	3.00	0.479	15.0	0.096
0.95	1.46	3.50	0.411	20.0	0.072
1.00	1.39	4.00	0.360	25.0	0.058
1.10	1.27	4.32	0.333 (⅓ Octave)	30.0	0.048
1.20	1.17	4.50	0.320	35.0	0.041
1.30	1.08	5.00	0.288	40.0	0.036
1.40	1.01	5.50	0.262	45.0	0.032
1.414	1.00 (1 Octave)	6.00	0.240	50.0	0.029

Table 1 - Q Vs Bandwidth In Octaves

The above table is based on that provided by Rane ^[ 12 ] in their technical note 170. The notes also provide the formulae if you want to make the calculations yourself. Naturally, this only applies to bandpass filters, but it's a useful reference so has been included. Also shown are the three most common filter bandwidths used for 'graphic' equalisers, namely 1 octave, 1/2 octave and 1/3 octave. Some signal analysis software also includes sharper (higher Q) filters, but these aren't shown.

All filters are described by their 'order' - the number of reactive elements in the circuit. A reactive element is either a capacitor or inductor, although most active filters do not use inductors. In turn, this determines the ultimate rolloff, specified in either dB/octave or dB/decade. Most filters do not achieve the theoretical rolloff slope until the signal frequency is perhaps several octaves above or below the design frequency. With high Q filters, the initial rolloff is faster than the design value, and vice-versa for low Q filters.

In addition, filters are classified into two distinct groups - odd and even order. Each behaves differently, and this often needs to be accounted for in the final design. The general characteristics are shown below ...

Order (Poles)	dB/Octave	dB/Decade	Phase Shift *	Comments
1^st	6	20	90°	Only passive, very common
2^nd	12	40	180°	Extremely common - most popular
3^rd	18	60	270°	Moderately common
4^th	24	80	360°	Linkwitz-Riley crossovers (etc.)
5^th	30	100	450°	Uncommon - rarely used
6^th	36	120	540°	Uncommon
n	n × 6	n × 20	n × 90°	Anti-aliasing filters (etc.)

Table 2 - Filter Orders and Rolloff Slopes

You'll see that the first order filter is passive only. While an opamp is often used with these filters, it is only a buffer. While it is certainly possible to build an active 1st order filter, the Q still can't be altered. The filter's Q and rolloff are fixed by the laws of physics and cannot be changed. All other filters allow a choice of Q, modifying the initial rolloff slope and creating a peak (high Q) or gentle rolloff (low Q) just before the cutoff frequency. By definition, the cutoff frequency of any filter is when the amplitude has fallen by 3dB from the normal output level. If there is a peak in the response, this is ignored when stating the nominal cutoff frequency.

This can be rather confusing to the newcomer, because the formula may show a nominal cutoff frequency of (say) 1.59kHz, yet the measured response can differ considerably. In general, any formula given for frequency assumes Butterworth response. The table below is for second order filters, but the overall Q is the same for all filter orders above the first (these always have a Q of 0.5).

Type	Q	Damping	Description
Bessel	0.577	1.733	Maximally flat phase response, fastest settling time
Butterworth	0.707	1.414	Maximally flat amplitude
Chebyshev	> 0.707	< 1.414	Peak (and dips) before rolloff. Fastest initial rolloff

Table 3 - Filter Types and Characteristics

The above covers the most important and common filter classes, but the Q can actually be anything from 0.5 ('sub-Bessel'), up to often quite high numbers. Few filters for normal usage will have a Q exceeding 2, and a Sallen-Key filter will become an oscillator if the Q exceeds 3. Extremely high Q factors are generally only used with bandpass and band stop (notch) filters.

It's common to see references to poles and zeros with filters, and this can create difficulties for beginners in particular. This isn't helped at all when you are faced with complex calculations, vector and/ or Bode plots and somewhat convoluted explanations that usually don't help when you're starting out. This isn't at all surprising when you are dealing with digital or notch filters, but it is rather daunting when you see the mathematics involved. I don't intend to cover this in any great detail because mostly it won't help you understand if you see a bunch of vector diagrams but few 'real life' examples. Explaining filters in terms of s-parameters, Neper frequencies (and/ or Nepers/ second) and phase shift in radians/ second doesn't really help anyone to understand the basic principles!

Only first order filters are discussed in this overview, having an idealised rolloff of 6dB/ octave or 20dB/ decade. These are the simplest of all filters, and only require an opamp to ensure that loading on the filter circuit is minimal. They cannot drive any external load without changing their behaviour (however slightly that may be). Filter circuits are often described by a mathematical equation called a transfer function, which in general form is a formula with variables denoted as 'j' and 'ω' where ...

This is where things go pear-shaped, because √-1 is an impossible number (you can't take the square root of a negative number), and is classified as the 'imaginary' part of the equation. Some calculators allow what's often known as 'complex' arithmetic/ maths, which permits the use of imaginary numbers to allow 'complex' equations to be solved. The 'imaginary' part of the equation represents the reactive element (a capacitor or inductor), while the 'real' part usually represents resistance, which is not reactive.

For example, one can determine the output voltage of a first order low-pass filter at any frequency with the equation ...

Long before simulators were available to the average user, this was the only way that one could determine the output voltage of a filter circuit at any given frequency. It's still necessary if you need to calculate the input or output impedance of even a simple resistor/ capacitor (RC) filter (unless you use a simulator of course). If you don't have a calculator that handles 'complex' maths (i.e. one that can handle j-notation) then basically you have a great deal of work to do! The common formula ...

... provides the -3dB frequency, but at any other frequency it isn't easy to determine the output voltage or phase without delving into complex maths. Everyone had to use scientific calculators that had the ability to work with the 'imaginary' part of the equation, and to say that the process was tedious is putting it mildly (in the extreme). It's a long time since I used this particular form of calculation (and yes, I still have a couple of scientific calculators with that facility), and most of the time it's not necessary any more ... if you have a simulator of course. Even without simulation tools, much of what you actually need to determine is still simply based on the 3dB frequency, and the rest tends to follow common rules that don't change. At least, this is the case with simple filters, but it becomes a lot more difficult when you're designing filters with characteristics that differ from the 'normal'.

Zeros in a filter are a different matter again. There are some extremely tedious calculations involved if you're writing code for a filter to be implemented in a DSP, but somewhat predictably this isn't a topic I intend to cover. I will only describe zeros in the most simplistic sense - it's not strictly accurate (at least not with more advanced filter techniques), but it's intended as a very basic introduction only.

As an example, we'll examine one of the most common 'complex' first order filter networks, the RIAA equalisation curve for vinyl playback. The original filter (as opposed to the IEC 'amended' version) has two poles (at 50.05Hz and 2,122Hz), and one zero at 500.5Hz. Although we're only interested in the zero (since that where this explanation is headed), the two poles and the zero are shown below. You will also see these frequencies described in terms of time constants, being 75µs, 318µs and 3180µs for 2122Hz, 500Hz and 50Hz respectively.

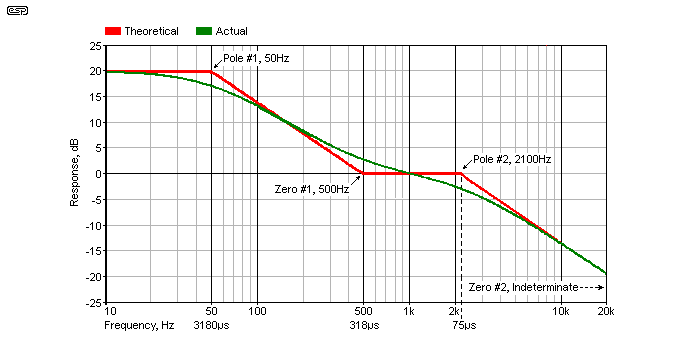
Note that the frequencies have been rounded to the nearest whole number, so 50.05Hz is shown as 50Hz. In some designs, there's a second zero at some indeterminate frequency above 20kHz. This is not part of the RIAA specification, and is the unintended consequence of using a single stage to perform the entire equalisation (this flaw does not exist in Project 06). It happens because the single stage EQ arrangement cannot have a gain below unity (although the reasons are outside the scope of this section).

As you can see, the zero at 500Hz effectively stops the rolloff as frequency increases. Because filters are 'real world' devices, the theoretical response (in red) can never be achieved. The recording EQ has the same generalised response, but is inverted (it has two zeros and one pole). In the case of an RIAA playback filter, the zero at 500Hz simply stops the rolloff - if no high frequency (2,122Hz) de-emphasis were applied, the response would flatten out above ~1kHz, with a theoretical level of 0dB (in reality it will be somewhat less, at around -2dB or thereabouts).

Interestingly (or not

) a high pass filter will always have an 'implied' zero at DC. By definition, a high-pass filter must be unable to pass DC, because it uses one or more capacitors in series with the input signal. Since an ideal capacitor cannot pass DC (and most film caps approach this ideal), this always sets the output to zero at DC, although the response may already be attenuated to the point where the DC component is immaterial anyway.

If you want to know more on this area of filter design, there are some references below, or do a search on the topic of filter poles and zeros. I can pretty much guarantee that most people will stare blankly at the descriptions offered and be none the wiser afterwards, hence this brief introduction to the subject. There is no doubt that people who really like maths will find the explanations enlightening, but most people just want to be able to design simple circuits that work. The remainder of this article shows you how that can be done.

In general, it is preferable wherever possible to operate all opamps in an audio circuit using a dual power supply. Typically, the supply rails will be ±15V, although this may be as low as ±5V in some cases. While a single supply can be used, it is necessary to bias all opamps to a voltage that's typically half the supply voltage.

This may be done individually at the input of each opamp, or a common 'artificial earth' can be created that is shared by all the analogue circuitry. In either case, all (actual) ground referenced signals must be capacitively coupled, and it is probable that the circuit will generate an audible thump when power is applied or removed. For the purposes of this article, all opamps will be operated from a dual supply. Supply rails, bypass capacitors and opamp supply connections are not shown. If you need to run any of these filter circuits from a single supply, you will need to implement an artificial earth and all coupling capacitors as needed.

This is now your responsibility, and you can expect me to become annoyed if you ask how this should be done. I suggest that you read through Project 32 for a simple split supply circuit that can be used with the filters shown here.

You will need to verify the pinouts for the opamp(s) you plan to use. For general testing, TL072 opamps are suggested, as they are reasonably well behaved (provided the peak input level is kept well below the supply rail voltage), have very high input impedance so filter performance is not compromised, and are both readily available and cheap. Experimentation is strongly recommended - you will learn more by building the circuits that you ever can just by reading an article on the subject.

Supply pins, bypass capacitors and power supply connections are not shown in any of the circuits that follow. A 100nF multilayer capacitor should be used from each supply pin to ground (artificial or otherwise) to ensure that the circuit doesn't oscillate. You will also need to include a 100 ohm resistor at the opamp's output if you plan to connect any of the filters shown to shielded cables (for example to a monitor amplifier). Failure to include the resistor may result in the opamp(s) oscillating.

Selecting the right values is more a matter of educated guesswork than an exact science. The choice is determined by a number of factors, including the opamp's ability to drive the impedances presented to it, noise, and sensible values for capacitors. While a 100Hz filter that uses 100pF capacitors is possible, the 15.9M resistors needed are so high that noise will be a real problem. Likewise, it would be silly to design a 20kHz filter that used 10uF capacitors, since the resistance needed is less than 1 ohm.

E12	1.0		1.2		1.5		1.8		2.2		2.7		3.3		3.9		4.7		5.6		6.8		8.2
E24	1.0	1.1	1.2	1.3	1.5	1.6	1.8	2.0	2.2	2.4	2.7	3.0	3.3	3.6	3.9	4.3	4.7	5.1	5.6	6.2	6.8	7.5	8.2	9.1

Table 4 - E12 and E24 Component Values

Capacitors are the most limiting, since they are only readily available in the E12 series. While resistors can be obtained in the E96 series (96 values per decade), for audio work this is rarely necessary and simply adds needless expense. The E24 series is generally sufficient, and these values are usually easy to get.

Where possible, I suggest that resistors should not be less than 2.2k, nor higher than 100k - 47k is better, but may not be suitable for very low frequencies. Higher values cause greater circuit noise, and if low value resistances are used, the opamps in the circuit will be prematurely overloaded trying to drive the low impedance. All resistors should be 1% metal film for lowest noise and greatest stability. Capacitance should be kept above 1nF if possible, and larger (within reason) is better. Very small capacitors are unduly influenced by stray capacitance of the PCB tracks and even lead lengths, so should be avoided unless there is no choice.

Capacitors should be polyester or Mylar. Never use ceramic caps except when nothing else is available - if you must use them, use NP0 (C0G) types if possible. Since close tolerance capacitors are hard to get and expensive, it's easier to buy more than you need and match them using a cheap capacitance meter. Absolute accuracy usually isn't needed, but close matching between channels for a stereo system is a requirement for good imaging.

Unless there is absolutely no choice, avoid bipolar (non-polarised) electrolytic capacitors completely. They are not suitable for precision filters, and may cause audible distortion in some cases. Tantalum caps should be avoided altogether!

Sallen-Key filters are by far the most common for a great many applications. They are well behaved, and reasonably tolerant of component variations. All filters are affected by the component values, but some are more critical than others. The general unity gain Sallen-Key topology can be very irksome if you need odd-order filters, and changing the Q of the unity gain filters will subject you to a barrage of maths to contend with. Nothing actually difficult, but tedious.

... however, this is modified (sometimes dramatically) once we start using filters of second order and higher.

A modification that allows equal component values and lets the Q be changed at will is easily applied, provided you can accept a change of gain along with the change of Q. Sometimes this is not an issue, but certainly not always. The majority of filters shown in ESP's project pages use unity-gain Sallen-Key filters, but in most cases the required values are already worked out for you. Figure 3.1 shows the traditional Butterworth low and high pass unity gain filters.

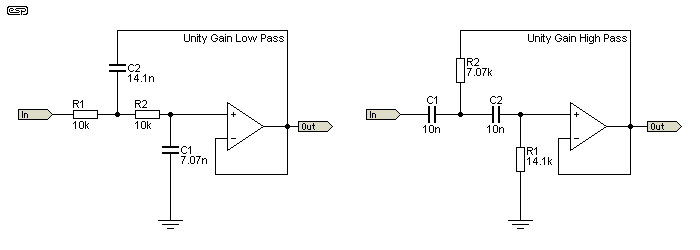
This is the standard unity gain Sallen-Key circuit. The values are set for a Q of 0.707, so the behaviour is Butterworth. The turnover (-3dB) frequency is 1.59kHz. As you can see, for the low pass filter we change the value of C (10nF) as follows ...

Exactly the same principle is applied to the high pass filter, except that the standardised value for R (10K) used here is modified by Q, with R1 becoming 14.14k and R2 becomes 7.07k. In many cases, it is necessary to make small adjustments to the frequency to allow the use of standard value components.

If all frequency selecting components are equal (equal value Sallen-Key), the Q falls to 0.5, and the filter is best described as 'sub-Bessel'. This is shown below, along with response graphs showing the difference. For calculation, there are countless different formulae (including interactive websites and filter design software), but all eventually come back to the same numbers. I have chosen a simplistic approach, but it is worth noting that the final values are definitely not standard values. This is very common with filters, and it may take several attempts before you get values you can actually buy (or arrange with series/parallel arrangements).

This version uses nice equal values, and is the easiest to build. However, because the Q is so low, it is not generally considered to be useful (although it is used for the 12dB/ octave Linkwitz-Riley crossover network). The relative response of the Butterworth and sub-Bessel filters are shown in Figure 3.3.

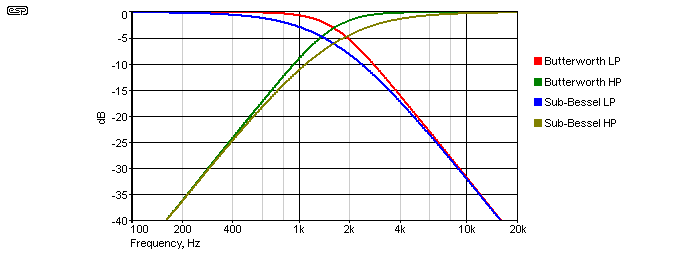
With a Q of 0.5 (damping of 2), the sub-Bessel filter has a very gradual initial rolloff. The crossover frequency between high and low-pass sections is at -3dB for a Butterworth filter, but is -6dB for the sub-Bessel type. Note that a true Bessel filter has a Q of 0.577, hence the distinction here. This is not always adhered to, as some references indicate that a Bessel filter simply has a Q of less than 0.707 (or damping greater than 1.414). While it may seem pedantic, I will stay with the strict definition in this area.

A useful (but relatively uncommon) change to the Sallen-Key filter allows us to obtain a much more flexible filter. This is a very useful variant, but the added gain may be a problem in some systems. While it is possible to use it as unity gain (see below), there are still limitations.

By adding a feedback network to the opamp, we can change the gain and Q of the filter without affecting the frequency. The Q of a filter using this arrangement is ...

Once the gain is known, the values of R3 and R4 can be determined. Since gain is calculated from ...

As a result, the circuit in Figure 3.4 has a gain of 1.586 and a Q of 0.707 as expected (or close enough to it). It is generally considered that the gain and Q are inextricably linked, but there is no real reason that the output can't be taken from the junction of R3 and R4, via a high impedance buffer (unity gain non-inverting opamp buffer). This restores unity gain, but remember that the opamp is still operating with gain, so there is a requirement to keep levels lower than expected. From ±15V, most opamps will give close to 10V RMS output, but this is reduced to a little over 6V RMS (at the junction of R3 and R4) when operated this way.

For a Bessel filter, gain will be reduced to 1.267 (R3 = 2.67k), and for Chebyshev with a Q of 1, the gain is 2 and R3 = R4 = 10k. Remember that the Sallen-Key filter must be operated with a Q of less than 3 or it will become an oscillator.

For most applications in audio, it's difficult to justify the extra complexity of any other filter type. The Sallen-Key has established itself as the most popular filter type for electronic crossovers, high pass filters (e.g. rumble filters or loudspeaker excursion protection) and many others as well. It does have limitations, but once understood these are easy to work around and generally cause few problems.

Multiple feedback (MFB) filters are most commonly used where high gain or high Q is needed - especially in bandpass designs. The design calculations can be extremely tedious, and there is regularly a requirement for component values that are simply unobtainable (or extremely messy - using many different values). The performance is usually as good as a Sallen-Key circuit, but one extra component is needed for a unity gain solution.

While it is accepted that gain, Q and frequency are independently adjustable, this is only really true at the design phase. Again, there is a requirement for widely varying component values. The MFB design is very well suited to bandpass applications though, and its simplicity is hard to beat in that application. You may see MFB filters referred to as Deliyannis, Delyiannis, Deliyannis-Friend or just 'DF'. These are the same as shown here but with a different name.

Notably, the high pass MFB filter has an input impedance that falls with frequency, and it can easily become so low as to overload both the driving opamp and the opamp used for the filter itself. In the circuit shown below, input impedance for the high pass falls to 1.6k at 20kHz - it can be far lower if the filter is tuned to a lower frequency, because the capacitor values are larger. If the caps are changed to 50nF and 100nF (giving a high pass filter tuned to 159Hz), the input impedance falls to just 320 ohms at 10kHz if Rs1 and Rs2 are not included. For the most part, the capacitive loading makes the high-pass version pretty much useless, due to the extreme likelihood of serious distortion at high frequencies and/or instability.

The loading is so high that it's almost guaranteed to cause most opamps stress, and distortion will rise rapidly as frequency increases (remember - this is within the pass band of the filter). At the same time, the opamp's open loop gain is falling because of its internal frequency compensation, so distortion rises far more than expected. The additional resistors do reduce the level slightly, but that's a small price to pay if distortion can be reduced to an acceptable level. Don't expect to find this in many text books, but it's a fact nonetheless ^[8]. Ultimately, it's best to avoid using high pass MFB filters unless there is absolutely no choice - Sallen-Key has none of the problems described. (Note that the low-pass MFB filter has no bad habits and is quite safe to use.)

Figure 4.1 shows low and high pass versions of the MFB filter. These are both set for a -3dB frequency of 1.59kHz, and based on 10k and 10nF tuning components. Look carefully at the high-pass filter, and you can see the capacitive feedback path. Rs1 and Rs2 can be added to isolate the capacitance, but will reduce the level. The safe value depends on the opamps used, and you'll lose a little over 0.6dB in the pass band with the values shown above. The loss can be reduced (but input impedance is also reduced) by using a lower value for Rs1 and Rs2. Note that Rs1 and Rs2 are both needed, and must be the same value.

Using the normal frequency formula, R =10k and C = 10nF, but these values don't work properly in the MFB filter. Since we know that Q = 0.707 for a Butterworth filter, we can simplify the component selection quite dramatically as shown below. What? It doesn't look simple? The normal formulae are a great deal more complex than the method described here.

As with the Sallen-Key filter, it will generally be necessary to change your expectations of the cutoff frequency to allow the use of available component values. Fortunately, it is rarely necessary in audio applications to have very precise frequencies, so minor adjustments are usually not a problem. Using the MFB filter for a crossover network is usually not a good idea though, because you end up with too many different values, increasing the risk of making assembly errors. Because the filter is also slightly more complex, it will be more expensive to build.

It's difficult to recommend the MFB high pass filter because of its extremely low input impedance and capacitive load on the driving stage at high frequencies. Although adding the resistors as shown mitigates this problem, it's far easier to use a Sallen-Key filter which doesn't have the problem.

Bandpass filters are commonly used for various effects, constant-Q graphic equalisers and parametric EQ circuits. They are also used with analogue analysers and various pieces of test equipment. Where fixed frequency and Q are needed, the MFB bandpass filter is difficult to beat, as it is a straightforward design with no bad habits.

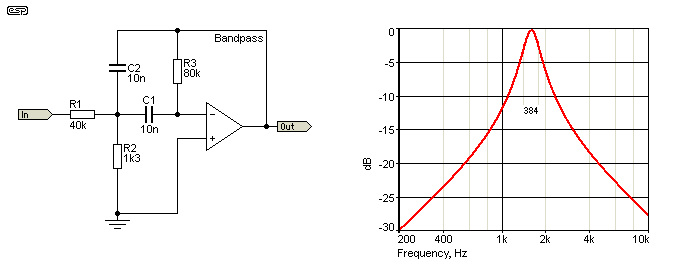
As before, the filter is tuned to 1.59kHz, and we can measure the Q to verify that it's what we expect. For a bandpass filter, Q is equal to the peak frequency, divided by the -3dB bandwidth (384Hz), so Q = 1590 / 384 = 4.14 - that's pretty close, considering that the resistor values were rounded to the nearest sensible value. The values were obtained from the ESP MFB Bandpass Filter Calculator (available on the ESP website).

This filter is used in Project 84 (a one third octave band subwoofer equaliser) and is also referenced in a number of other projects. I suggest that you use the calculator to work out the values, since the formulae are somewhat beyond the intent of this article.

I (recently) became aware of a simplified version of the MFB bandpass filter, which uses one less resistor. This makes it less useful overall, but that's not to say that it should not be used. As with all things in electronics, there's more than one way to do something, and despite some limitations the simplified version is a handy tool where you don't need great flexibility.

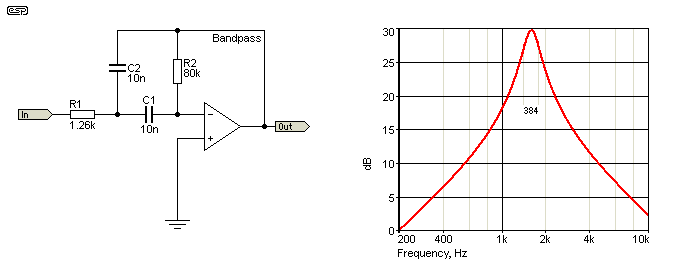
I kept the frequency and Q the same, but we don't have the ability to vary gain and Q independently with one resistor missing. The parallel combination of R1 and R2 in Fig. 4.2 is 1.26k, so a single 1.26k resistor is used for the input. Because we can't control both gain and Q, we get a gain of 30dB (×31.8). While this might be far too high for some circuits, it will likely be fine in others, particularly if we have a low input level (less than 250mV at the tuned frequency). If we don't mind the Q changing, the circuit can be tuned over a limited range by making R1 variable. If R1 is varied from 1k to 2.2k (for example), the frequency is changed from 1.78kHz to 1.2kHz, but the gain changes too - 32dB with 1k, 25dB with 2.2k. The Q changes too, but not by a great deal.

The state-variable filter is something of an oddball design, with several different versions of the basic circuit being available, and different formulae being described to calculate the gain and Q. All of the frequency calculations I've seen are correct, but some imply that multiple resistors are involved to change frequency. This is not the case - two resistors affect the frequency, and these can be in the form of a dual-gang pot. This makes the filter easily tunable, unlike any of the others so far.

In addition, the state-variable filter provides 3 simultaneous outputs - high pass, low pass and bandpass. All have the same frequency (-3dB or peak for the bandpass) and the same Q. It is often said that gain and Q cannot be separated - so as one is varied, the other varies as well. Q and gain can be made independent by adding a fourth opamp. This is desirable (and commonly applied) in parametric equalisers.

This is an extremely versatile filter, and its usefulness is often overlooked. Some reference material suggests that there's no real reason to even use the design, but I disagree with this assessment. Since both low and high pass outputs are available simultaneously, it can be used as a variable crossover (with some changes). While higher orders can be made, they become more and more complex, and for this article only the second order filter is discussed.

In the example above, R1 changes gain and Q. Increasing R1 reduces gain, and increases the filter's Q, although the change of Q is relatively small compared to the gain change. R2 changes Q, but leaves gain unchanged (contrary to the myriad claims that the two are inseparable without the fourth opamp). Increasing R2 reduces Q, and vice versa.

Rt and Ct are the tuning components, and as shown give a frequency of 1.59kHz. The two Rt resistors can be replaced by a dual-gang pot, allowing a continuous variation of frequency. A series resistor must still be used, typically one tenth of the pot value. In the above circuit, Rt could be replaced by a 100k pot in series with a 10k resistor, giving a range from 145Hz to 1.59kHz - a range of just over 1 decade. When the frequency of a state variable filter is changed, the Q remains the same.

A notch filter is created by adding the high and low pass outputs. Because they are 180° out of phase at the tuning frequency (fo), the result is (close to) zero voltage at fo when the two outputs are added. Addition can use a traditional opamp summing amplifier or just a pair of resistors. There will be a 6dB signal loss across the pass band for the simple resistive adder. The depth of the notch depends on how accurately the two signals are summed, but even a small phase shift (through the filter) can considerably reduce the depth.

It is beyond the scope of this article to cover the complete design process, and in particular the process for setting the filter Q to a specific value. There are countless examples and design notes available on the Net, and those interested in exploring further are encouraged to do a search for material that gives the information needed.

For a lot more info on this topology, see the ESP article State Variable Filters. This includes the little-known 1^st order variant.

Although the state-variable filter is a bi-quadratic (biquad) design, it is different from the 'true' biquad shown here. The biquad in its pure form is somewhat remarkable in that it can only be made as a low pass or bandpass filter. There is no ability to use the traditional approach of swapping the positions of tuning resistors and capacitors to obtain a high pass filter. This limits its usefulness, but it is still very usable as a bandpass filter. Like the state-variable, both outputs are available simultaneously. In addition, there is an inverted copy of the low pass output, however this is probably of limited value.

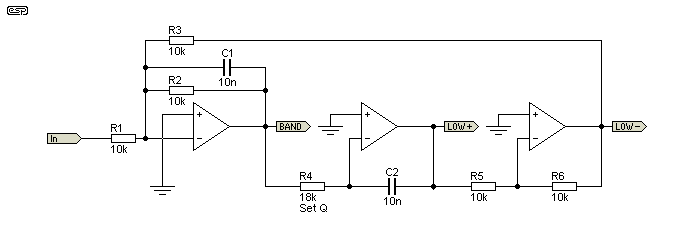
While the circuit looks similar to the state variable, it is very different. Again, a complete discussion of the calculations is outside the scope of this article, but R2 is used to set Q and gain, while R3 & R4 and C1 & C2 are the tuning components. When the frequency of a biquad filter is changed, Q also changes, so a bandpass implementation has a constant bandwidth. Q increases with increased frequency. Use as a low pass filter is rather pointless, since there is no high pass equivalent, and the Q changes with frequency anyway. R4 sets the Q, and with 18k as shown, it's a little above 0.707 (Butterworth). Unfortunately, adjusting the Q also changes the frequency. As the resistance is lowered, the frequency and Q increase.

You can swap the positions of R4 and C2 to get a high-pass and low-pass output, but the slope is only 6dB/ octave and you lose the bandpass (it becomes the low-pass output). This isn't a useful modification.

Notch filters are used for a variety of purposes, including distortion analysers and for removing troublesome frequencies. 50/60Hz hum or prominent acoustic feedback frequencies can be reduced (or eliminated almost completely), because typical notch filters have a very narrow band-stop region. The bandwidth can be as low as around 10-20 Hz, with the unwanted frequency reduced by 40dB or more.

There are many circuit topologies that can be used for very narrow notch filters, including the twin-T, Fliege, Wien-bridge and state-variable. All have similar responses, but the twin-T is unique in that it can have an almost infinite notch depth even when configured as a completely passive filter (i.e. with no opamp or other amplification). All other types require active circuitry to achieve usable results.

The twin-T notch requires extraordinary component precision to achieve a complete notch, and for this reason it's not often recommended. However, it is without doubt one of the best filters to use when a very deep notch is needed - especially for completely passive circuits. The following is only a very brief overview of notch filters - there are many more configurations that can be used, each with its own advantages and disadvantages. Notable (but not shown) is the bridged-T filter that has been used in some distortion analysers. It is easier to tune than the twin-T, and comes in a number of different topologies. It's interesting, but IMO not sufficiently useful to describe here. Bridged-T notch filters can never equal a twin-T for notch depth or Q without the addition of active circuitry.

I have heard complaints that the twin-tee notch filter is 'finicky' to set up. In reality, it's no harder that any other filter type with similar performance. If a very deep notch is needed at a particular frequency, the filter component values will always be critical, and even a small drift of a component value (due to time or temperature) will affect the notch depth at the selected frequency. In many respects, the twin-tee is likely to win out over any other design, because it can achieve a very deep notch with no active components. Feedback is only ever needed to minimise the -3dB frequency bandwidth, and it does not affect the notch depth.

The twin-T (or twin-tee) filter is essentially a notch (band stop) filter, and unlike most filters shown here, can still give an extremely high Q notch without the use of any opamps. In theory, the notch depth is infinite at the tuning frequency, but this is rarely achieved in practice. Notch depths of 100dB are easily achieved, and are common in distortion analysers. If the notch is placed at the fundamental frequency of the applied signal, it is effectively removed completely, so any signal that is measured is noise and distortion. While a notch filter can be converted to a peaking (bandpass) by means of an opamp, the result is usually about the same as you can get with a MFB filter, so there's not much point because of the added complexity.

It is still common to add an opamp to a twin-t filter though, because it makes it possible to ensure that there is little or no attenuation of the second harmonic when used as the basis for a distortion analyser. By applying feedback around the notch filter, the response can be maintained within a dB or less at only one octave from the notch frequency.

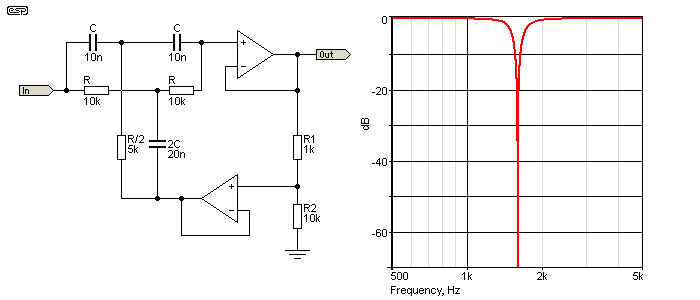
R and C are the tuning components. These have to be extremely accurate for a very deep notch, and it's common for one of the R values and the 2R value to be made using a fixed resistor and two (or more) potentiometers. For example, 10k might be made using a 9.95k fixed resistance, in series with a 500 ohm and 50 ohm pot. The idea is that at the nominal tuning frequency, the two pots will be centred, allowing fine and very fine adjustment. A change of as little as 10 ohms makes a big difference to the notch depth.

The first opamp acts as a buffer, ensuring that the output of the filter is not loaded by the voltage divider that supplies the signal to the second opamp. The second opamp applies feedback via the R/2 and 2C leg of the tee, making the initial rolloff occur closer to the notch frequency. As shown, the second harmonic is attenuated by less than 0.3dB. When used to remove the fundamental frequency for distortion measurements, it can be extremely difficult to maintain a good notch because of minute amounts of frequency drift.

The bridged-tee (bridged-T) notch is often used for equalisation, and other places where a fairly shallow (and broad) notch is acceptable. Strictly speaking, it's not an active filter, other than the requirement for a high impedance output buffer. The bridged-tee filter has a wide band where frequencies near the tuned frequency are affected, and very deep notches are not available with most versions. There are a few different topologies, but they are generally intended to provide a specific response rather than act as 'true' notch filters. The bridged-tee can be used as the tuned feedback path for an oscillator, but there's little or no advantage over a Wien bridge in this role. Note that the circuit must be driven from a low impedance source.

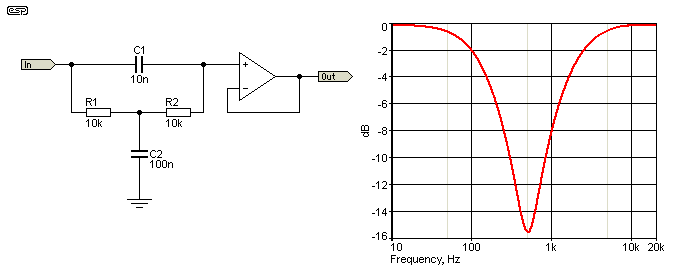
The circuit above is more-or-less typical, and also shows the response with the values provided. Calculation of the frequency is non-intuitive and a bit cumbersome, but it's easy enough when you know how. The ratio between the two capacitors is defined by the cap values, and as shown they are 10:1 (C2, C1 respectively, shown below as C_ratio). To determine the frequency we must take the square root of the ratio, in this case, √10 is 3.162. This means the effective (or 'nominal') capacitance is C1 × 3.162 =31.62nF or C2 / 3.162 =31.62nF. Frequency is ...

Turning the first two formulae around makes it easier to calculate the capacitor values needed for a defined frequency ...

The attenuation at the tuned frequency is set by the capacitor ratio, and for the example shown ...

However, as you can see from the graph in Figure 6.2, the 'notch' is very broad, with -3dB frequencies at 126Hz and 1.97kHz, a bandwidth of 1.844kHz. Increasing the capacitance ratio achieves a deeper notch, but all other frequencies (outside the 'stop band') are also attenuated. While the bridged-tee is useful for some specific applications (EQ circuits in particular), it's too broad to be useful for eliminating 'nuisance' frequencies such as mains hum. There is no reason that the values of R1 and R2 must be equal, and it's not uncommon to see different values used in equalisation circuits.

The bridged-tee is very sensitive to output loading, so a high impedance buffer is essential at the output to prevent the levels above and below the tuning frequency from being 'skewed'. Any output load will reduce the level below the notch frequency. The alternative version described below is more sensitive to output loading than the conventional arrangement, but neither is much use without a buffer.

An interesting twist on the 'conventional' bridged-tee shown above is to reverse the positions of the resistors and capacitors. You might expect that this would reverse its operation, and provide a peak rather than a notch. It actually works identically to the version shown above. For example, for the same frequency and notch depth, use a 100k resistor in place of C1, and a 10k resistor in place of C2. Two equal value caps (10nF each) replace the resistors. The potential advantage is that it's more flexible, because resistors are available in a wider range than capacitors. While you could replace one resistor with a pot, that will affect both notch depth and frequency, so it's not especially useful. The tuning formulae are the same, except that it becomes the resistor ratio rather than the capacitance ratio that determines frequency and attenuation.

It's not at all uncommon to see bridged-tee network with unbalanced values, deliberately driven with a non-zero source impedance and/ or loaded at the output. One of the places you are most likely to come across the circuit in bass guitar amps as a 'contour' circuit, which deliberately inserts a notch and (usually) bass boost. Further discussion of this is outside the scope of this article.

Normally, the Fliege filter is something of an oddity (high and low pass versions are shown below), but it makes an easily tuned notch filter with variable Q. Notch depth is not as good as a twin-T, but is much better than the bridged-tee. It can be tuned with a single resistor (within limits). The Q can be changed by changing two resistors. There is a caveat on the variable Q though - if the frequency tuning resistance is changed, the Q is also changed.

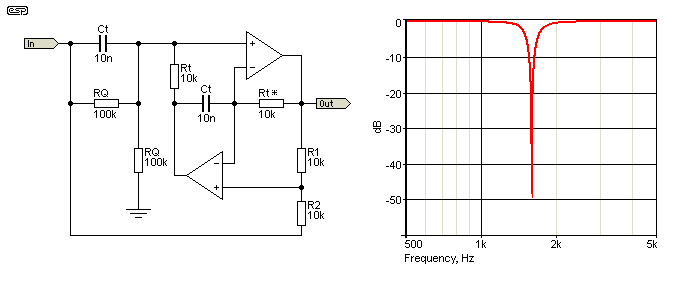
As before, the frequency with component values shown is 1.59kHz, and follows the same formula as other filters. Q is set by resistors RQ, and the value needed is approximately ...

In the circuit shown, Q is about 5, and that's enough to ensure that the second harmonic of the input frequency is attenuated by less than 0.1dB. Increasing the Q will reduce the notch depth, so the lowest Q that gives an acceptable minimum attenuation of harmonics should be used. It is possible to increase the Q to at least 10, but notch depth will be reduced.

The circuit can be tuned over a reasonable range by varying the resistor Rt* - it can be changed from 5k to 20k, providing frequencies from about 2.25kHz down to 1.13kHz with the other values unchanged. The Q does vary (as does notch depth), but performance is satisfactory over the range. I don't know of any other notch filter that's so easily adjusted, which makes this an excellent candidate for removing any 'nuisance' frequency such as 50/60Hz hum.

Fliege notch filters have unique phase performance. As frequency increases towards the notch frequency the phase is 0° - in phase with the input. As the notch frequency is passed, the phase is -360° above the notch - again exactly in phase with the input. No other notch filter I've looked at does this.

There are many, many more filter types. Some are extremely obscure (but interesting), and there are no doubt others that richly deserve their obscurity. It would not be sensible to even try to cover them all, and with a few exceptions most will never be even considered as candidates for your next project. Some of the better known types are covered, others are mentioned only in passing.

The Fliege filters shown below are interesting - gain is fixed at two, but the frequency and Q are (at least to some extent) independent. The Q can be changed with a single resistor scaled to the frequency tuning resistors, as shown below. If RQ is half the value of Rt (the tuning resistor) the Q is 0.5 - a Linkwitz-Riley alignment.

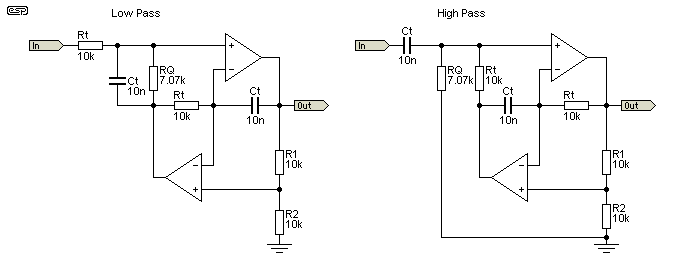
Frequency is set with Rt and Ct, and they are conveniently the same values we'd use for a single pole filter. RQ sets the filter Q (surprise), and if set to 10k in the example, the Q is 1. When set to 7.07k as shown, the Q is 0.707 - very easy and convenient. Considering the requirement for two opamps, it's unlikely to be adopted for crossovers or many other audio applications, but it is interesting nonetheless (or at least I think so). Fliege filters can also be configured for bandpass or notch.

Another obscure design is the Akerberg-Mossberg Filter. This is an easy topology to use, but requires three-op-amps for its operation. It is easy to change gain, type of low-pass and high-pass filter (Butterworth, Chebyshev or Bessel), and the Q of band-pass and notch filters. The notch filter performance is not as good as that of the twin-T but it is supposedly less critical. While undoubtedly useful, the details will not be included here, because there seems little application for audio circuits.

One filter that does require further explanation is the Cauer or elliptic filter. As the basis for the NTM™ (Neville Thiele Method) crossover, and a very common anti-aliasing filter for analogue-digital conversion, it deserves some attention. It is an interesting filter, in that it is the only one to have ripple in the stop band. Pass band ripple is common with high-order Chebyshev filters, but no other filter has ripple in the stop band - beyond the cutoff frequency. This is produced because the filter is typically a combination of a (more or less) traditional Sallen-Key filter, followed by one or more notch filters, all tuned to operate beyond the cutoff frequency.

The following example uses a Sallen-Key 12dB/octave filter, followed by a state variable filter. The summing amplifier adds the high pass and low-pass outputs together, resulting in a notch because they are out-of-phase. Changing the value of R13 (68k) changes the position of the notch ... a lower value reduces notch frequency, but increases the level of the rebound (see Figure 7.3).

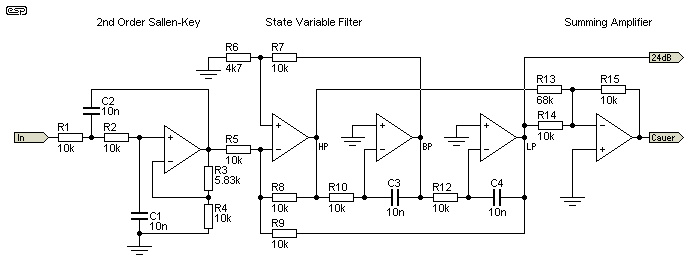
Only the low pass filter is shown - the requirements for a high pass equivalent are met by the usual technique of reversing resistors and capacitors for the primary frequency, and changing the frequency for the notch filter(s). Admittedly, this is not especially easy, but a complete description of both types is not warranted here.

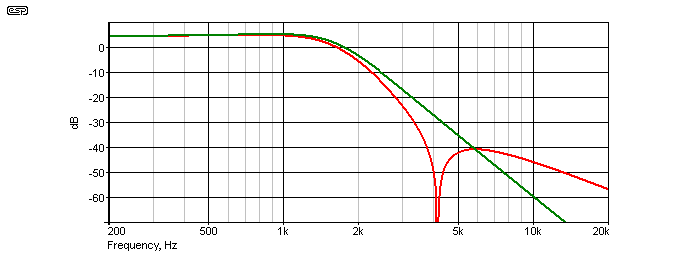
The red trace is the Cauer response - as is immediately obvious, it rolls off more sharply than the fourth order filter after the cutoff frequency, but 'rebounds' at about 6kHz. While the rebound (or bounce) appears disconcerting, with higher order filters it's not really a concern. Even here, the peak level is at -40dB. Note that the rolloff slope after the bounce is 12dB/octave, not 24. This is because the state variable filter is used to produce the notch, and does not add a further 12dB/octave. The green trace shows the level when the state variable filter is used as an additional 12dB/octave filter, giving 24dB/octave in total.

The turnover frequency is a little lower than the 1.59kHz expected (1.48kHz), but that's because the filter was optimised for the 24dB/octave response shown in green. The faster rolloff of the Cauer filter is very pronounced, especially beyond 3kHz. At 4kHz, the level is 44dB below that at 2kHz, but it would be incorrect to say that the rolloff was 44dB/octave, because it changes - very rapidly as the notch frequency is approached (4.1kHz in this example).

While I have only shown a basic 24dB/octave version, it's not uncommon for Cauer filters to be 6^th order or above. As the order is increased, the bounce is reduced further, and this is common for anti-aliasing filters. The much-sought-after 'brick wall' filter is almost achieved with this topology.

Inductors are without doubt the worst of all electronic components. Not only are they bulky, but they pick up noise from any nearby source of a magnetic field. Inductors also have significant resistance and often high inter-winding capacitance as well. When used for RF applications, the values needed are typically very low and it's easy enough to minimise the deficiencies. For audio frequencies, the failings of inductors make themselves well known.

One solution for 'line level' applications, where the voltage and current are low, is the simulated inductor. By configuring an opamp and capacitor appropriately, the combination can be made to act just like a real inductor, but with fewer shortcomings. This is commonly known as a simulated inductor or a gyrator. When used with a capacitor, 'traditional' LC (inductance-capacitance) filters can be created, and these are common building blocks in many filter applications.

The generalised circuits are shown below, one using only an emitter follower (cheap and cheerful) or the 'real' alternative using an opamp. The response shown is based on the generalised circuit shown below the two gyrators. It's a parallel resonance circuit with a 10k feed resistance. The formula for resonance is also shown in the drawing. Gyrators can be used as an inductor only, or in series or parallel resonance circuits ... provided the 'inductor' is earth/ ground referenced.

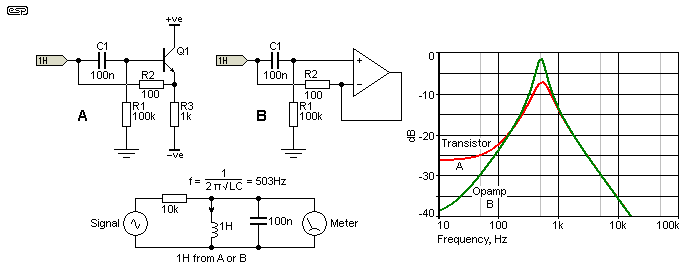
As you can see from the response graph, the single transistor version is nowhere near as good as that using an opamp. However, it's cheap, and in many cases will work just fine - depending on your application of course. In reality, the cost difference is minimal, because most opamps are inexpensive (and you save one resistor as well). The basic formula for determining inductance is ...

For the above example, the simulated inductors are nominally 1H, but the transistor version is actually slightly less because the gain of an emitter follower is typically only about 0.98 instead of unity. The circuits can be wired for series or parallel resonance, but the 'inductors' are earth (ground) referenced. If you need a floating inductor, there is a circuit that can be used, but it's considerably more complex. For a great many equalisers and the like needed in audio, having the inductor earth referenced is not usually a problem.

Simulated inductors are not immune from 'winding resistance', but it is fairly obviously not because of the resistance of a coil of wire. R2 is needed for the circuit to work, and is directly equivalent to winding resistance. Although some opamps will be able to work with values lower than the 100 ohms shown, there is a risk of instability if R2 is made too low. In general, 100 ohms is a reasonable compromise, and works well in practice.

If you wish to know (a lot) more about this approach, see the Gyrator Filters article, which covers them in much greater detail that this short introduction.

It's hard to think of this as a filter, since it leaves the frequency response unchanged. Only the phase of the signal is varied, and with this comes a potentially useful time delay. Although the delay is short, it can be used to 'time align' drivers whose acoustic centres are separated far enough to cause problems.

Version 'A' produces a lagging phase. That means that the output signal occurs after the input. For the values shown, the delay is about 155µs with a 1.59kHz signal. Version 'B' has a leading phase - the output signal occurs before the input. While this seems impossible, for a signal that lasts more than a few cycles it really does happen. In the second example, the output occurs 155µs before the input (but only after steady-state conditions are established).

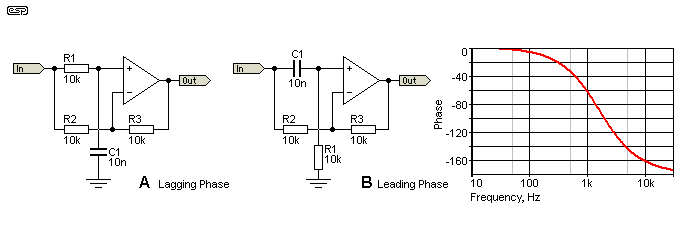
The circuit is shown above. It is a simple circuit, and easily incorporated into a system if needed. R1 and C1 can be exchanged as shown in 'B', which simply reverses the phase. Instead of having 0° shift at low frequencies, there is 180° and vice versa. The advantage of the second circuit is that R1 can be replaced with a pot, allowing the phase at 1.58kHz to be varied from 0° (pot shorted) to 180° to around 12° with a 100k pot. When the pot is set for minimum resistance, C1 is connected to ground, and may cause the driving opamp to become unstable. You need to verify that the driving circuit remains stable in your design.

The leading phase angle of the second circuit makes it unsuitable as a time delay - for that, you might use several of the 'A' circuits in series to get the desired time delay. It must be understood that the time delay is the result of phase shift, so varies with frequency. At one octave either side of 1.59kHz (i.e. 795Hz and 3.18kHz), the delay is roughly 180µs and 110µs respectively.

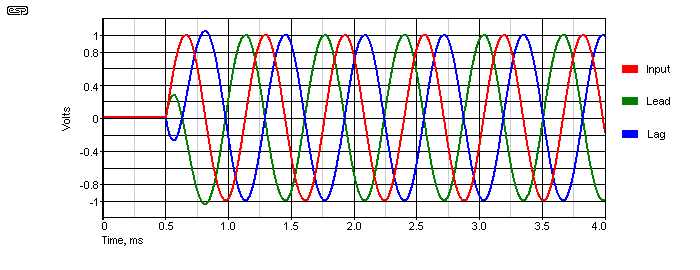
Above, you can see the input signal (red), and the outputs of the two versions of the all-pass filter (lead and lag). The time response is set up within half a cycle, so by the completion of the first full cycle, the leading and lagging time delay is clearly visible. The leading trace (green) is 159µs before the input, and the lagging trace (blue) is 159µs after the input. This amount of time may seem insignificant, but it represents the time taken for sound in air to travel about 55mm.

By adjusting the values to suit the crossover frequency, it is possible to obtain pretty close to perfect time alignment. This may be necessary if the acoustic centres of the loudspeaker drivers cause the relative outputs to be out of phase by less than 180°. It is usually the tweeter signal that has to be delayed to match the midrange (or mid-bass) driver. The details of how to achieve this are outside the scope of this article.

Digital filters are not new, but with cheap digital signal processor (DSP) ICs now available, they are becoming very common. In many cases, the end-user is completely unaware that digital filters are in use because they are commonly integrated within equipment. Surround-sound, room 'correction' (which cannot and does not work! ¹), tone controls and many other functions are now implemented using DSPs, rather than analogue circuits. Indeed, many of the functions (whether useful or not) can't even be done using analogue processing because the cost and circuit complexity would be far too high. Some filter implementations are simply impossible with analogue processing.

The design and implementation of digital filters is worthy of a complete book, and indeed there are many such books available. I do not propose to even attempt to explain these filters, other than in general terms. Although not exactly outside the scope of DIY, it requires dedicated hardware and software to calculate the filter coefficients and to program the DSP.

There are basically two different types of digital filter, known as 'finite impulse response' (FIR) and 'infinite impulse response' (IIR). Analogue filters are essentially IIR types, and the IIR digital filter coefficients are commonly derived from the analogue equivalent. All digital filters rely on digital delay lines, plus addition, subtraction and/or multiplication in software. Although all processes needed can be performed by general purpose processors, DSP chips are optimised for these functions so generally require far less code than would be needed for a DSP function performed by the general-purpose microprocessor in a home PC (for example). Basic digital filter characteristics are as follows ...

When a signal that is to be filtered is analysed, it's usually easy to decide which type of digital filter is best for the application. If phase characteristics are important, then FIR filters must be used because they have a linear phase characteristic. FIR filters are of higher order and more complex. If it's only the frequency response that matters (for example to replace an analogue filter), IIR filters may be a better choice because they have a lower order (less complex), and are therefore easier and cheaper to implement. While there are many claims that phase is somehow 'important', that is often not true at all. Relative phase (between two frequency bands for example) is important, but is not an issue with IIR filter implementations if done properly.

FIR filters have the advantage that they are always stable, but they require greater hardware resources. FIR filters use a mathematical function referred to as convolution - where the final function is a modified form of one of the two original functions. FIR filters have no analogue counterpart, and can be designed to do things that are impossible with any analogue filter. An example is to build a filter with a steep rolloff slope, but with linear phase shift (even if it's not needed for audio).

IIR filters use recursion (feedback), and while this makes the functions more efficient (requiring fewer computing resources), it also means that the final filter may not be stable. IIR filters are virtually identical to conventional analogue filters, and it is not possible to remove phase shift from the output.

A filter using convolution (FIR) requires a separate processing section and delay for each sample being processed, and uses only the input samples in the equations. In contrast, a recursive filter (IIR) uses both input and output samples because of the feedback, and therefore requires fewer processor resources. As noted, this can lead to instability and also 'limit cycles' - basically a form of non-harmonic distortion resulting from quantisation errors that may circulate within the DSP filter block.

It has been claimed (for example ^[11]) that digital filters are far superior to analogue filters because they "are not subject to the component non-linearities that greatly complicate the design of analogue filters". While this is true up to a point, it also ignores the fact that digital filters are subject to quantisation errors and all the other issues that all digital systems can suffer from. Not the least of these is headroom. Most DSPs operate from 5V or 3.3V, so the level is limited to an absolute maximum of 1.77V or 1.17V RMS, more than 15dB lower than can be used with analogue filters using common opamps.

However, as noted above, digital filters can have far greater rolloff slopes and much higher complexity than analogue equivalents, and FIR filters can be configured as linear-phase so there is minimal phase shift through the filter. Digital filters can be configured to do things that are simply impossible with an analogue design. Because digital filters rely on signal delay, there is an inevitable latency (time delay) as the signal passes through the filter, analogue to digital converter (ADC) and digital to analogue converter (DAC). Most digital filters also require an analogue low-pass filter ahead of the ADC to prevent aliasing.

Some proponents of the digital approach may claim that the FIR filter's linear-phase characteristic is ideal for audio. However, it should be remembered that the phase of a typical audio signal is virtually random, and eliminating phase shift is of no practical benefit. There is no evidence that the normal phase shift introduced by any (sensible) analogue filter is audible in a blind test.

Overall, the digital approach is likely to cost more for typical audio applications such as electronic crossovers. There are DSP boards available that can easily be configured as crossovers, with optional equalisation in some cases. The end result may well be very good, but it's close to impossible to truly understand what's going on, and little is learned along the way (other than how to drive PC based software to configure the DSP).

Because of the low output level which may not be sufficient to drive a power amp to its maximum, additional analogue circuitry is needed to restore the level, and the digital circuitry must be operated at a level that guarantees that 0dBFS (maximum digital (full scale) level without clipping) is never exceeded. This might mean that the maximum level may need to be kept below perhaps 500mV, and most of the time the level will be a great deal less at normal listening levels.

Of course, once the signal is in the digital domain (after the ADC), any other effects that might be needed are easily accomplished. For example, a digital crossover network can be configured with the necessary time delays to 'time align' the loudspeakers, or to apply equalisation as needed to obtain a flat frequency response. Great care is still required though, because it's easy to apply radical EQ to 'correct' a poor loudspeaker, and while the end result might be flat, it may also sound like a bucket of bolts. Despite claims you may see, digital processing cannot make a silk purse from a sow's ear - a crappy speaker is still crappy no matter how much technology you throw at it!

Digital filters can be used to re-create any analogue response (Butterworth, Bessel, Linkwitz-Riley, Chebyshev, 'inverse' Chebyshev, elliptic (Cauer), low pass, high pass, band pass, band stop (notch), etc., etc. As explained above, responses and functions can be created in the digital domain that are simply impossible with analogue. Despite all the apparent advantages, it does not follow that digital is necessarily 'better'. Indeed, if the DSP isn't capable of at least 32-bit precision the digital realisation may be a great deal worse, and there is always the additional circuitry (and low signal level requiring additional amplification) that just means that there are a great many more things to go wrong.

There is no doubt that digital filters are immensely useful, and it's expected that entire subsystems will become more powerful and cheaper over time. It's already possible to get fully configured boards and software to drive them quite cheaply (less than $100), and these will eventually replace many analogue designs. Whether they are 'better' than an analogue implementation for 'routine' applications such as electronic crossover networks is subject to some debate - as is to be expected. As always, many of the claims and counter-claims are based on purely subjective testing, without a great deal of science. Most readers will know that I consider subjective claims to be pointless at best, and they are often highly misleading.

I do not propose to cover digital filters in any more detail than has been presented. People who are interested in more information are encouraged to do a web search - there is a vast amount of information available. Be warned that much of what you will find is extremely technical, and assumes that the reader is already acquainted with digital techniques and understands the complex maths involved. It's worth noting that I've sold a great many Project 09 analogue crossovers to people who've tried DSP and were disappointed with the results when listening to music. Unless the DSP has a sufficiently high sample rate and bit-depth, digital 'artifacts' are more likely than not, made worse when complex functions are implemented.

As noted earlier, all filters affect the transient response of the signal passed through them. As the order and Q are increased, the transient response becomes worse, with clearly visible ringing on an impulse waveform. While this can often look very scary ("that must ruin the sound"), in reality it's not really a problem for most of the filters we use. Part of the problem is that the typical test waveform is a pulse, and while that does show the problem, it makes it appear much worse than it really is. Music does not consist of very narrow pulses that have infinitely short rise and fall times, but tends to be relatively smooth. Even musical transients do not have very fast rise times, because the instruments do not have fast rise-times and the recording process uses filters to limit the maximum frequency. This reduces the maximum possible risetime of any signal that passes through.

Although it is possible to record a single 50µs pulse (half a cycle of 10kHz), loudspeakers can't reproduce it even if it were to get through the recording chain. We would also be hard pressed to hear it - such a signal would only sound like a click, provided the level was high enough of course. It takes time before the ear-brain combination can recognise that a signal exists as a tone or the sound of an instrument. Nevertheless, transient response will be examined here, warts and all.

More to the point, while the 'standard' test signal shows the effect, it is totally unrealistic. Being of only one polarity, it is completely unlike any normal signal in audio. There is no musical instrument that can produce such a waveform, and no microphone that can record it intact.

The term 'steady-state', if used strictly, describes a waveform that has existed for eternity. Any disturbance (such as switching it on or off) introduces transient effects. In most cases, steady-state conditions can be seen to exist after a number of cycles of a sinewave. Minor disturbances will not usually be audible, because the signal needs to exist for a period of several cycles before we can interpret it as a particular tone. This is highly dependent on the frequency and amplitude of the signal and its harmonics.

The impulse used for the above was a 1V peak, 200µs wide impulse (green trace). The filter used was 24dB/octave with a cutoff frequency of 1.66kHz, and is approximately Butterworth. Even a Linkwitz-Riley alignment shows a (very) small amount of ringing, but it is negligible in real terms. The red trace shows that the filter is triggered into a heavily damped oscillation at a frequency just below the cutoff frequency (in this case, at about 1.3kHz). As Q is increased, the ringing becomes worse, but since high Q filters are not generally used in audio, they can be ignored for the purposes of this article.

What is more important is the overall change to a normal signal. While music is not steady-state, for most filters it takes only a couple of cycles for steady-state conditions to be established. For the filter used for Figure 9.1, it takes only one half-cycle at 1kHz before the output signal reaches (approximately) steady-state conditions. When the input signal is above the cutoff frequency, it takes a little longer for the signal to settle down - at 2kHz, 2½ cycles are needed before steady-state conditions apply. This gets progressively worse as frequency is increased, but the filter is also reducing the amplitude of the signal above cutoff, so the effects become immaterial. For example, we don't really care if it takes 3 days for a 20kHz signal to settle from a 1.66kHz filter, because the filter has effectively removed the signal anyway (20kHz is about 88dB down with the test filter).

A high pass filter also affects the transient response. Figure 9.2 shows the same pulse, applied to a 70Hz, 24dB/octave high pass filter. Again, the red trace is the filtered response, and green is the applied pulse. Again, because the test impulse is unidirectional, the effects shown are far worse than will ever be experienced by a real filter handling music signals. The majority of the disturbance seen is a direct result of using a single pulse of only one polarity.

While it is simple enough to create a somewhat more realistic test waveform, there really isn't much point. The simple fact is that filters affect transient response, and it does not matter if they are active, passive or digital. Passive filters are the hardest to control, and if the load is a loudspeaker it presents a different impedance depending on frequency, and will therefore be far less predictable.

Suffice to say that all filters create deviations in transient response, but provided filter Q is kept reasonably low, the effects are generally completely inaudible. Filters with a Q of 0.5 (sub-Bessel) are as close to benign as it is possible to achieve while still maintaining useful frequency response and crossover performance. Low frequency high pass filters (for example, infrasonic filters, speaker excursion limiting filters, etc.) introduce phase shift (as do all filters), but their transient response does not usually significantly affect signals within the normal audio range.

While transient response is obviously important, I can find no evidence that listeners are able to detect any statistically relevant differences in a properly conducted blind test. Vast numbers of people listen to vented (ported) loudspeaker enclosures, and their transient response is dreadful. However, it must be considered that bass signals hardly qualify as 'transient', because they are rather slow by nature. While commonly used by reviewers, the term 'fast bass' is an oxymoron.

Because it's pertinent to this discussion (and because I can do it easily), I recorded the waveform distortion of a 723Hz 3-cycle tone burst, passed through a 723Hz 6dB/octave filter (2.2k and 100nF). This is the most benign of all filters, yet the waveform distortion is clearly visible in the above two oscilloscope captures. The image on the left is the high-pass section, and on the right is the low-pass. Note that the input waveform is exactly 3 cycles, and it starts and stops at exactly zero volts.

This is a more realistic test than using a single polarity pulse, but the waveform is still easily able to show the effect, but it will never be found in isolation in music. This notwithstanding, the effect of the filters is audible, as you would expect from any filter. There is also a phase shift of 90°, with the high pass output leading the low pass output. A single 3 cycle burst sounds like a click, but at 723Hz the tonality of the signal is just audible. There is also an 'undertone' created by the stop-start nature of the waveform. The filter changes the sound simply because it is a filter. The low pass filter accentuates the non-harmonic 'undertone' that is created by the burst waveform, and the high pass version removes it.

This shows quite clearly that even a first order filter (6dB/octave) will cause transient distortion. The above results can be duplicated easily, and a simulation gives identical results to those captured on the oscilloscope. For those who remain dubious, I recommend that you either run the test yourself if you have the equipment, or at least perform simulations to verify that these effects are very real. A tone-burst gate is shown in Project 143, and Project 86 describes a simple audio oscillator. Both are ideal for this type of test.

Higher order filters do exactly the same thing, but the effects are more pronounced. However, even a 24dB/octave (4th order) filter will show the second cycle from both high and low pass sections to be exactly equal and in phase with each other. Only the first and last cycles are affected in a tone-burst test. Note that any waveform disturbance when the tone burst ends is always after the input stimulus has ended (the filter is not pro-active, and can't make a change before the stimulus has started or stopped). Lest the reader assume from this that a full-range driver is 'better' because it needs no crossover network, these have many other compromises and will rarely (if ever) match a decent 2-way or 3-way system using active crossover networks.

Of all the filter orders, only first order (6dB/ octave) types will produce an output waveform that's identical to the input when the outputs of high-pass and low-pass filters (tuned to the same frequency) are recombined. This is often used as a 'reason' that we shouldn't use anything else, but first order filters are almost always too gentle to be useful for the majority of applications.

Filters affect the phase of the signal, and in so doing also affect the time it takes for the signal to pass through the filter. This time is called 'group delay', and is described in the next section.

Group delay is best described as the delay difference between one group of frequencies and another different group of frequencies (e.g. above and below 2kHz). To use the analogy of John L Murphy (True Audio), imagine if the treble was heard instantly, but the bass was delayed until the same time tomorrow (24 hours). This would be audible to everyone. All normal filters (and even some loudspeakers

) can be expected to have a delay much less than this, and group delay is not generally a problem.

Above we see a Butterworth (red) and sub-Bessel (green) filter. Only the low-pass section is shown, and only as a matter of interest. There is nothing that can be done to change group delay for a given filter type, and if that filter type is needed to produce a specific response then you are simply stuck with it. Like phase shift, group delay comes free with all filters as a matter of course.

There is a table (below) that gives the approximate thresholds of audibility for group delay, and the data were compiled by Blauert and Laws ^[7]. There is not a lot of research into this for some reason, but there's little or nothing that can be done about it. The group delays of most filters are well below the threshold of audibility based on the available data.

Frequency	Audibility Threshold	No. of Cycles
500 Hz	3.2 ms	1.6
1 kHz	2 ms	2
2 kHz	1 ms	2
4 kHz	1.5 ms	6
8 kHz	2 ms	16

Threshold of Audibility for Group Delay

The table shows the minimum group delay that is thought to be audible, along with the number of cycles at that frequency. Any delay time less than shown will not be heard, however there may be exceptions if the delay causes an anomaly in the frequency response. If this is the case, it will be detected as a frequency response error - not a time delay. Although there appears to have been surprisingly little testing in this area, it is generally thought that human hearing is not especially sensitive to short time delays. As frequency is increased or reduced around 2kHz (the most sensitive frequency), greater delays are required before they become audible.

Audibility of group delay depends on the source material. Sharp impulse sounds can sound 'blurred' if there is too much delay between the low and high frequencies, but you may not hear any significant change if the source material has no transients. It's probably safe to assume that if the group delay never exceeds (say) 0.5 of a cycle at any frequency, it won't be audible. This is a far stricter criterion than we see in the above table, but it's not unreasonable. Some speaker designers consider that up to two complete cycles is "probably ok" (and they are probably right), and a typical vented speaker enclosure (the vent, box and loudspeaker create an acoustic filter) has far more group delay than most filters.

One complete cycle at 50Hz is 20ms, so two cycles will take 40ms. At 20Hz, a single cycle is 50ms and two cycles take 100ms. You can work out the cycle time for any frequency and take it from there. In the table above, anything over 1.6 cycles at 500Hz is at the threshold of audibility, but at sub-bass frequencies (below 40Hz) our hearing is not at all sensitive to the delay. There is little or no empirical data though, and the above table is pretty much all that anyone has to work with ... you'll find the same data all over the Net.

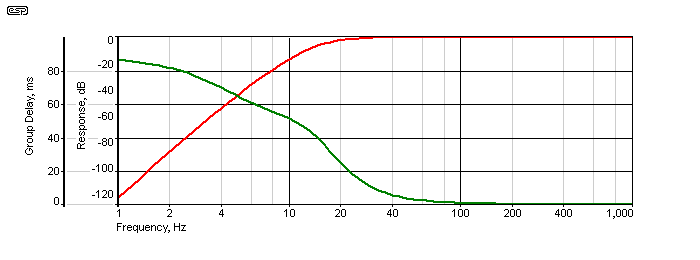
Figure 10.2 shows the group delay for the P99 36dB/octave infrasonic filter. This is a very high rolloff filter, and the group delay looks pretty bad at 1Hz ... until you realise that the theoretical output level at that frequency is -120dB. Group delay is 24ms at 20Hz (50ms cycle time), 29ms at 18Hz (55.5ms cycle time) and 51ms at 10Hz (100ms cycle time). This is close enough to the 1/2 cycle limit that I set above, and will normally be completely inaudible. Room effects and enclosure design will cause far more havoc than a 1/2 cycle delay.

It also has to be understood that if you have a serious problem with infrasonics (for example), then a filter can only improve matters. Anything that fixes a known (and audible) problem can only ever improve the system overall. It's very rare that the cure is worse than the disease.

As most readers will be aware, nothing in life is perfect. While active filters are almost always preferable to their passive equivalents at audio frequencies, there are limitations. Many of these are due to the opamp used in the filter circuit, although it doesn't often show up during simulations or real-life testing. However, it is important that these limits are known, because in some circuits it can make a big difference.

Every opamp has a limited frequency response and a non-zero output impedance. The main reason for frequency response upper limit is the internal stabilisation capacitor, although it may be external with some devices. Either way, the open loop gain (and frequency response) falls at 6dB/ octave at frequencies above a lower limit of between 10 and 1,000Hz. This stabilisation feedback is necessary to ensure that the opamp doesn't oscillate, and needs to be fairly brutal for stable unity gain operation. If an opamp is properly selected, high pass filters usually behave exactly as expected, but low pass filters may show sub-optimal performance in the stop band.

The reduced HF gain has two effects - because there is less feedback, distortion is higher and output impedance rises. Any low pass filter that relies on a low opamp output impedance will eventually fail to maintain the desired rolloff rate, and will 'bottom out' at a frequency determined by the opamp's characteristics. The Sallen-Key low pass filter is particularly susceptible to this issue, as shown in the following drawing and graph. Some other filter topologies are also affected, including the multiple feedback bandpass. MFB low pass filters are slightly affected, but not as badly as the Sallen-Key. Rather than the signal showing a 'rebound', the slope changes from 12dB/ octave to 6dB/ octave when the opamp runs out of steam.

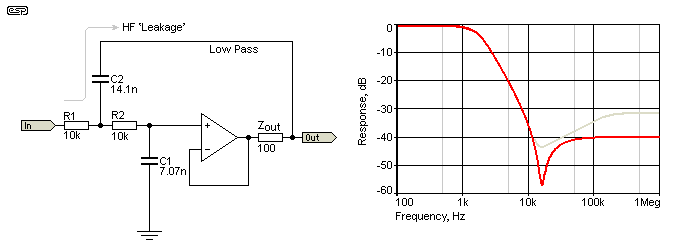
The output impedance of the opamp is exaggerated for clarity, but the effect is very clear. the -3dB frequency is 1.59kHz as before, and the dip occurs at 16kHz. As the frequency increases further, the output level is eventually determined solely by the combination of R1 and Z_out, which forms a simple voltage divider in the example circuit. At the frequencies where we see problems, C2 has a very low impedance (710 ohms at 16kHz), and C1 becomes more-or-less redundant because the opamp can't do anything useful any more.

The real-life situation is more complex of course, because Z_out is not a simple resistance and it increases with increasing frequency as the opamp runs out of gain. This is shown in the light grey trace. The 'rebound' level will not continue to increase indefinitely though, but the only way to know exactly what the circuit will do is to build it. A simulator can only ever get you part of the way.

The important things to understand here are that a) this is very real, and b) it rarely causes a problem. That might come as a surprise, but at audio frequencies the transition frequency (where the output voltage stops falling at 12dB/ octave) is almost always well outside the audio band. For example, a lowly TL071 opamp has a transition frequency of 100kHz, where the signal is 66dB down. Yes, as the frequency is increased so is the output level, but there is no audio signal at 100kHz and we shouldn't be concerned that the level has risen to perhaps -40dB at 2MHz.

For audio frequencies, very few opamps (even the worst possible examples) will 'bottom out' at a frequency much less than around 50kHz, showing clearly that the example shown is very pessimistic. However, even with the result shown above, performance is not really compromised. At the worst, the output level is 40dB down, so with a 1V input the output at frequencies above 50kHz is still less than 10mV. Since there is no audio at that frequency, there's still no problem. However, it would not be sensible to use the worst possible opamp, and any opamp designed for audio use will be far better than shown. When filter sections are cascaded, the result is that the 'rebound' occurs at a much lower level. For a 24dB/ octave filter, the rebound level will typically be below the noise floor, even for signals above 100kHz.

Where this effect does become important is when one is building or designing test equipment or signal processing circuits that operate at frequencies well above the audio band. Naturally, if this is the case, we will choose a wide bandwidth opamp that's designed for the frequency range that we need. Expecting most 'audio grade' opamps to function properly even at low radio frequencies would be folly.

As with all things in electronics, the effect can be mitigated (or at least minimised) by suitable trickery. For example, we can include a first order filter in front of the main filter circuit, having a turnover frequency that's perhaps 10 to 20 times the design frequency. So, a 1.59kHz filter could have a preceding 6dB/octave filter (with an impedance of less than 1/10th of the primary filter) tuned for some suitably selected higher frequency. In the above example, that would add a series resistor in front of R1 of (say) 560 ohms, followed by a 3.9nF cap to ground (about 73kHz turnover frequency). With this in front of the circuit shown, even a µA741 will achieve an ultimate attenuation of at least 60dB below the reference level (at least according to the simulator I use). The additional filter does change the response ever so slightly, but the effects of that will need to be determined at the design phase.

Filters are an ongoing development, with DSP (digital signal processing) now being applied for more complex types. Regardless, the analogue versions are still very much in use, and for DIY applications are generally the cheapest and easiest to use. Performance is every bit as good as a DSP version, but they can't be changed with software coefficients because they must be hard-wired. Of course, many is the claim that digital filters are ever so much better than analogue, and there are just as many counter-claims. I don't believe that either camp is right - both can do the same things. As noted above, digital filters can do things that are impossible with analogue, but are significantly more complex and costly to develop. With the advent of high speed analogue-digital converters, even traditional anti-aliasing filters are often not needed, with a fairly basic filter being adequate. This is achieved by sampling the audio at a much higher than required rate, applying the filter digitally using a DSP, then down-sampling to the required rate (44.1kHz for example).

The hardware basis of analogue filters is rarely a problem for any fixed installation, such as a hi-fi system or a dedicated powered speaker, and the DSP approach is (generally) not cost effective. While even analogue filters can be made adjustable, it's very difficult to get 4-way (or more) ganged pots - and even harder to get them with acceptable tracking. However, it's easy to install machine sockets to allow resistors to be changed if this is needed.

Because of the huge range of different filter types, there is one to suit every need, however obscure. While some of those shown above are suitable for use as a crossover, others are completely unsuitable - often for reasons of cost and complexity. There is no point building a complex filter whose Q can be varied without affecting anything else, because you generally know the Q that's needed for your application before you start. This is determined by the filter topology and the requirements. For an electronic crossover, you need to be able to sum the outputs to get a flat response (generally an absolute requirement, because that's what the loudspeakers will do), so the Q needs to be set accordingly based on the filter slopes.

The Sallen-Key filter is still the easiest to use, and despite its shortcomings is sufficiently well behaved for almost anything needed in audio (for general purpose high and low pass filters at least). While MFB filters are sometimes applied, there is usually no advantage - the required values are more irksome, they are an inverting topology, and IMO offer no benefit to offset the greater complexity. High-pass MFB filters should be avoided altogether. Of course, bandpass MFB filters are ideal and beat most other contenders hands down. State variable filters are probably the most flexible, but need 3 opamps instead of only one for MFB or Sallen-Key types (for 12dB/octave or bandpass filters). The other topologies are interesting, but other than specialised applications, are generally not especially useful for audio/ hi-fi applications.

It's obviously necessary to ensure that the active element you use (usually an opamp) is up to the task. For example, using a µA741 for an RF filter would be ill-advised, because it simply isn't fast enough. Equally, using a very fast current feedback opamp designed for RF work would be just as silly in an audio circuit. The information here is simply an introduction to the various filter types and topologies, and it's up to the designer to select an opamp that will provide the best compromise for the intended application.

Notch filters are a somewhat unique application, especially the twin-tee. These are the basis of many distortion analysers, and this topology is the only passive R/C filter that offers a fairly high Q along with close to infinite attenuation of the tuned frequency. Adding feedback improves the Q, so the 'stop band' can be limited to just a few Hertz, with everything else passing through with little or no attenuation.

In short, there is an active filter for just about any audio frequency application imaginable, and it's up to the system designer to adopt the one(s) that best suit the specific needs of the final design. As noted earlier, the term 'audio frequency' does not mean 'audio' in the hi-fi sense, only that the frequency range is (mostly) within the audio spectrum (± a couple of octaves).

Several references were used while compiling this article, with many coming from my own accumulated knowledge. Some of this accumulated knowledge is directly due to the following publications:

Page created and copyright © Rod Elliott, 20 August 2009./ Update Jan 2014 - added digital filter overview plus Fig 17A and associated text./ Oct 2016 - Added section 11./ Jan 2019 - added section 1.2 (poles & zeros)./ Jan 2024 - Added Fig. 4.3 (simplified MFB bandpass).

Active Filters - Characteristics, Topologies and Examples