

|
| Elliott Sound Products | State Variable Filters |
 Main Index
Main Index
 Articles Index
Articles Index
One of the filter topologies I have mentioned in passing in other articles is the state-variable. This is one of the most versatile filter types available, but is often overlooked because it requires 3 opamps and must always be driven from a low impedance. Neither of these things is a challenge (most filters require a low impedance source anyway), and there is often no better solution to a filter problem than a state-variable type. It is derived from a two-integrator biquadratic topology (commonly referred to as a biquad), but has significant advantages. Not the least of these is the fact that the high and low pass signals are both available (a biquad provides lowpass & bandpass only) and at the same level. The bandpass output is also available, but its level depends on the filter Q.
State-variable filters can also produce a notch response by adding the high and low pass signals together without an inverter. Because they are 180° out of phase at all frequencies, the two signals cancel when their relative amplitudes are identical. Complete cancellation can only occur when both signals are present in exactly equal measure, so either side of the centre frequency the signal approaches the full level as you move further away from the notch frequency. With a Q of 0.707 (Butterworth alignment), the attenuation of the second harmonic is 3dB, but using a higher Q can reduce this. As with any notch filter there are limits, and ultimately frequency (and circuit component) stability are the limiting factors.
While it looks a little daunting at first, the circuit is actually quite straightforward. The first stage is used to add and subtract signals that are derived from a pair of integrators. There are three simultaneous outputs, low-pass, band-pass and high-pass. Unlike any other filter, the three outputs maintain a fixed phase relationship that remains true even if there are slight errors caused by component tolerances. In particular, the low-pass and high-pass outputs remain 180° out of phase regardless of (some) errors that may cause problems with overall frequency response. A simple inverter puts the two signals in perfect phase with each other.
The state-variable filter has many other unique properties too, so we shall look at them in some actual circuits. Note that these configurations are not the only ones applicable. State-variable filters are often shown quite differently, with input and Q-factor determining resistors in particular connecting to different opamp inputs. Q (quality factor) is also referred to by its inverse - damping (ζ), and ...
ζ = 1 / ( 2 × Q ) or ...
Q = 1 / ( 2 × ζ )
Therefore, a circuit with a Q of 0.707 (critically damped) also has a damping factor (ζ) of 0.707. It is very important to remember that inputs must always be from a low impedance source for any filter, and the state-variable is no different. Although not shown, all circuits shown below would have the input signal provided from a unity gain buffer or other similar circuit having very low impedance across the audio band.
The basic building block for a state-variable filter is shown in Figure 1. The first stage is the adder/ subtractor, which sums the outputs from the two integrators that follow. By varying resistor values, we can change the Q (bandwidth), gain and frequency. There are various schemes that are designed to allow at least Q and frequency to be changed at will, without affecting the gain.
This may not seem very profound at the moment, but the usefulness will be shown in further examples. The state-variable filter probably has more variations than any other type. The signal may be applied to either the inverting or non-inverting input of the first stage, the Q and gain can be changed by raising or lowering the values of several different resistors, or the Q can be varied without changing gain at all.
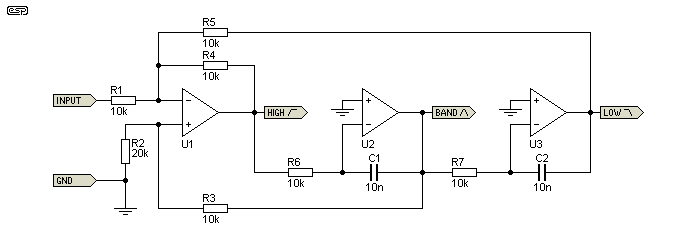
Figure 1 - Basic State-Variable Filter Schematic
U1 is the heart of the filter. It sums the signals returned from the two integrators, and resistor values change the gain and Q of the three outputs simultaneously. It is also the input (which may be on the inverting or non-inverting input for different results). U2 and U3 are the integrators, and R6/ C1 and R7/ C2 set the centre frequency.
To increase Q, reduce R2 (and vice versa) - passband gain is unchanged.
To reduce gain (and increase Q) increase R1
Note - although the passband gain is unaffected when R2 is changed, the gain at the filter's centre frequency is changed. For example, if R2 is reduced to 1k, the bandpass gain is over 11dB, and both high and low pass filters will peak to +11dB before rolloff starts. Well away from the tuning frequency, the high and low pass outputs return to the gain preset by the resistor value selection. You need to be aware of this, because it's very easy to cause clipping with high Q - even at normal (~1V RMS) input levels. While it's possible to get very high Q (50 or more), it's not advisable. In general, the Q shouldn't be greater than ten, otherwise the first opamp (U1) will run out of gain.
R4 and R5 should always be the same value. If one is increased or reduced, the relative levels of the high and low pass outputs can be changed, but it also affects Q and is not useful. R6 and R7 should also be the same, as should C1 and C2. Rather interestingly, changing R6 or R7 will alter the Q, but not the gain. Doing so also changes the frequency and the relative phase relationships between the two signals. To tune the filter properly, R6 and R7 must be kept equal (or as close as possible).
Provided that R6 = R7 and C1 = C2, the centre frequency is given by ...
1 / ( 2π × R × C )
For the values shown, centre frequency is 1,592Hz. R6 and R7 can be replaced with a dual gang pot, making the filter frequency variable over a wide range. This technique is used in crossover networks and parametric equalisers, and may also be applied to test equipment and anything else that benefits from a smoothly variable filter frequency. Good tracking is an essential requirement for a tuning pot. This generally means that you'll use a linear pot, because they generally have better tracking and linearity than log or antilog pots at the same price-point.
A bandpass filter's Q is defined as the centre frequency (fo) divided by the bandwidth (bw) at the -3dB frequencies. So if the centre frequency is 1kHz, the upper -3dB frequency is 1.66kHz and the lower -3dB frequency is 612Hz, the bandwidth is 1.05kHz. Therefore ...
Q = fo / bw
Q = 1k / 1.05k = 0.952
Conversely, if we know the Q then the bandwidth is given by ...
bw = fo / Q
bw = 1k / 0.952 = 1.05kHz
Note that the state variable filter shown here is a two pole design (second order), and therefore has a rolloff slope of 12dB/ octave. Fourth order filters (24dB/ octave) can also be made, but require a 4-gang pot to allow tuning, and are generally outside the scope of the hobbyist because the pots are too hard to get. The 4th order design is also considerably more complex and will not be covered here. Likewise, I don't intend to discuss a third order state variable (18dB/octave). The biggest problem you will face making anything over second order is the pots - dual gang pots are readily available, but multi-gang units are very hard to get.
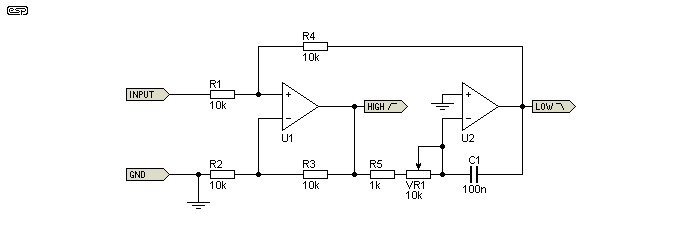
Figure 1A - First Order State-Variable Filter Schematic
However, a little known version is the first order state variable filter. This is the simplest of all, and is not often seen or used. I suggested it in the Project 152 Bass Guitar Amp (Part 2) because it's perfect for the job. U2 is the integrator, and tuning is via R5, VR1 and C1. With a 10k pot for VR1, you get a variable frequency from 144Hz (VR1 at maximum) to 1.59kHz (VR1 at minimum). Both high and low pass outputs are available, but there's no band pass output. The filter Q is fixed, and in common with all first order filters the outputs are 90° out of phase.
First order filters are generally of limited value because of the slow rolloff. The Figure 1A circuit is potentially useful because you get high and low pass outputs, and the frequency can be changed with a single pot. You may never see a first order state-variable filter again, but if you ever need one ...
If you wish to build a state-variable crossover, see Project 148, which is a complete 2 or 3-way crossover, and PCBs are available for it. I first started using a state-variable filter for an active crossover a long time ago (sometime in the mid 1970s), having found the filter topology described in a book and thinking "what a good idea - I'll build a crossover with it!" I used the crossover network based on the state-variable filter in my hi-fi for many years, and it found its way into several active crossovers I built for PA systems, and a test amplifier that I use to this day. The article 'Biamping - Not Quite Magic, But Close' was inspired by the continued success I had, and that article was the entire contents of my website in 1998 when it was first launched.
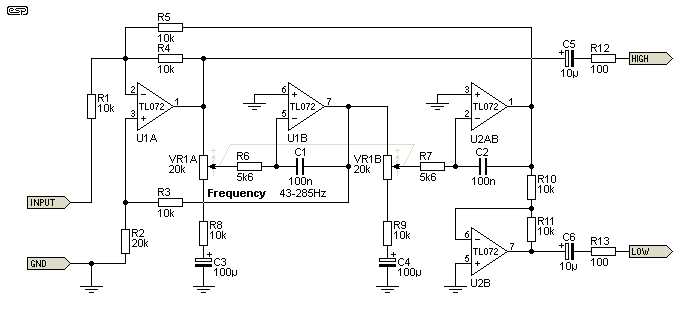
Figure 2 - State-Variable Filter Based Crossover Network
The circuit of Figure 2 is very similar to that used in my first crossover networks. I finally remembered the opamps I used originally - μA739¹ - remember that this was a very long time ago, before the acceptance of the venerable μA741! The TL072 is generally well suited to the state-variable topology for less demanding applications. Just about any opamp is suitable, but if bipolar input opamps are used noise may be an issue for the summing amp front end unless circuit impedances are kept low. There is always a balancing act (i.e. compromise) when selecting impedances - low impedance may reduce noise, but can overload the opamp's output leading to increased distortion.
¹ The Fairchild μA739 was a very early dual opamp that had an 'uncommitted' collector for the PNP output, and it used a load resistor from the output to the -ve supply to provide current for the output transistor. A shorted output meant instant death (for the opamp), as it had no short-circuit protection and it was not internally compensated. The same opamp was used in the Crown DC300A power amplifier (ca. 1970). Being 'pure' Class-A made it marginally better than other opamps of the day.
You will notice that the low-frequency output is provided via an inverter. This is because the high and low frequency outputs are 180° out-of-phase, so the inverter restores the correct phase relationship. This is standard with all 12dB/ octave filters - the inverter can be omitted if the low frequency loudspeaker is connected with reverse polarity, but this is not recommended when using an active crossover. The phase response is identical for both high and low pass sections, regardless of tuning resistor mismatches (caused by a poorly tracking pot) or variations in the system Q factor.
As shown, the crossover is continuously variable from 43Hz to 285Hz. Reduce the operating frequency by increasing C1 and C2, or increase it by reducing the cap values. The caps should be selected to be within better than 5% of each other if at all possible. In reality, the crossover is so good that small variations will be completely swamped by loudspeaker driver variations. At low frequencies, room nodes will cause huge variations, and the accuracy of the filters is almost irrelevant. This is not to imply that you can be cavalier and use any old part you like - it's still better to get things right  .
.
R2 changes the filter's Q, and with 22k there is a small error (0.26dB dip) when the outputs are summed. The optimum value for a Linkwitz-Riley alignment is 20k, but the error is so small that it is probable that it will never be audible. A traditional Butterworth response (replete with +3dB peak at crossover) is obtained by reducing R2 to 9k.
In case you are wondering, C3 and C4 are there to ensure that the filter has minimum gain at DC. The arrangement shown for the pots gives more range with a smaller value pot, but (without the capacitors) also increases the DC gain of the complete circuit. A small DC offset can be amplified considerably if the caps are omitted. However, with the traditionally low Q of crossover filters and correspondingly low total gain, it is more than likely that C3 and C4 can be omitted (i.e. replaced with a direct connection to ground) with no ill effects.
As noted, it is very important that the input is sourced from a low impedance, such as directly from another opamp. Any series resistance or impedance is added to the effective value of R1, and will change both gain and filter Q. For example, an extra 200 ohms will reduce the gain by 0.5dB and simultaneously cause a 0.5dB peak at the filter's centre frequency because Q is increased.
The frequency response of each output of a state-variable crossover is shown below. I have not included the summed response of the high and low pass sections, because a perfectly straight line is not very interesting. To obtain the straight line, the filter has a Q of 0.5 - Linkwitz-Riley alignment.

Figure 3 - State-Variable Crossover Frequency Response
The green trace is the bandpass output, and it's shown here only for interest's sake - not because it can be used in this configuration. The ultimate rolloff for the filters is 12dB/ octave, and while this is still useful, it's not a good as a 24dB/ octave Linkwitz-Riley crossover. As noted earlier, 24dB/ octave is possible, but the circuit becomes much more complex than a pair of Sallen-Key filters as used in Project 09. Note that the low-pass output is inverting with respect to the high-pass, but the bandpass output is in phase with the input. The low-pass output leads the input by 90°, while the high-pass lags the input by 90° at the tuned frequency.
A fourth order state-variable filter requires 5 opamps - one for the input stage as shown above, plus 4 integrators. Compared to the P09 crossover referenced above, this is both expensive and requires significant PCB real estate. While it can be tuned with a pot (unlike Sallen-Key filters), either a 4-gang pot or some means of switching 4 separate resistors is needed [ 1 ]. State variable filters are sometimes also built using VCAs in place of the pots, so you could use a SSM2164 quad VCA chip to control a fourth order filter.
While searching for useful additional material, I even came across a design for a third-order state-variable filter (18dB/ octave). While interesting, I cannot see a practical use for it other than for analogue synthesisers (for which it was designed).
One area that is most densely populated by the state-variable filter is the parametric equaliser. These are made by many different manufacturers, and up until fairly recently were analogue. Many modern ones are digital, or are software 'plug-ins' for PC based music editing programs. These equalisers are not to be taken lightly - in the wrong hands they can cause mayhem, because the filter bandwidth can be very narrow, but with a large amount of gain. As a notch filter, this is useful for reducing acoustic feedback (for example), but as a boosted band it can create feedback with ease. Some parametric equalisers allow the bandwidth to be as narrow as 1/6th of an octave or even less.
Parametric equalisers allow the user to apply boost or cut (attenuation), with one or more tunable filters. The filters are based on a state-variable topology, and are usually continuously variable across overlapping frequency ranges. The frequency, boost/ cut and bandwidth (Q) are all independently variable. While this provides great flexibility, it's easy to imagine how an untrained operator could seriously mess up the sound if given the chance. There's a 'golden rule' that applies to parametric EQ - "Cut narrow, boost wide." In other words, only use high Q filters to cut a troublesome frequency, and when applying boost, use a low Q.
The first design shown in Figure 4 is based on an article (original reference long lost) from 1982. It's interesting from an historical viewpoint, but it is a relatively complex circuit and requires two dual-gang pots. Both need to track accurately for good performance.
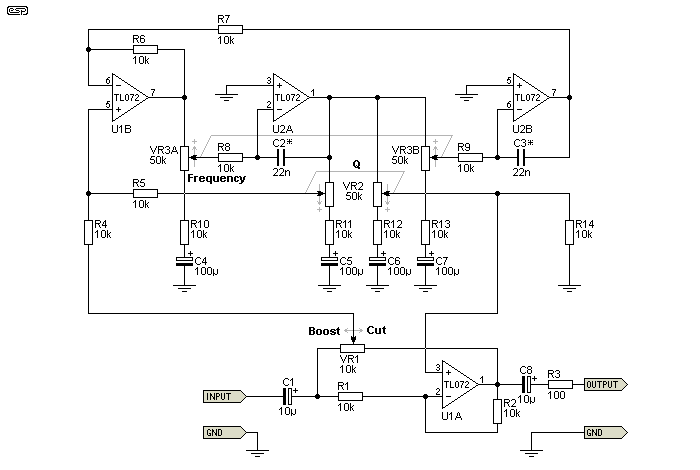
Figure 4 - Parametric Equaliser #1
The Q (bandwidth) is variable between a maximum of 7.8 (0.18 octave) and a minimum of 0.88 (1.56 octaves), and frequency with the values shown is from 66Hz to 722Hz. Gain remains constant as Q is changed. R11 and R12 can be reduced in value if a higher Q is desired, but Q cannot be less than 0.88 with the values given.
The second version is based on the Urei 545 parametric EQ [ 2 ], but I have made a number of changes. As you can see, it is much simpler than the circuit shown in Figure 4, and uses only one dual-gang pot. Q is now adjusted with a single ganged pot, but it is just as effective as the more complex version and does not change the gain at all.
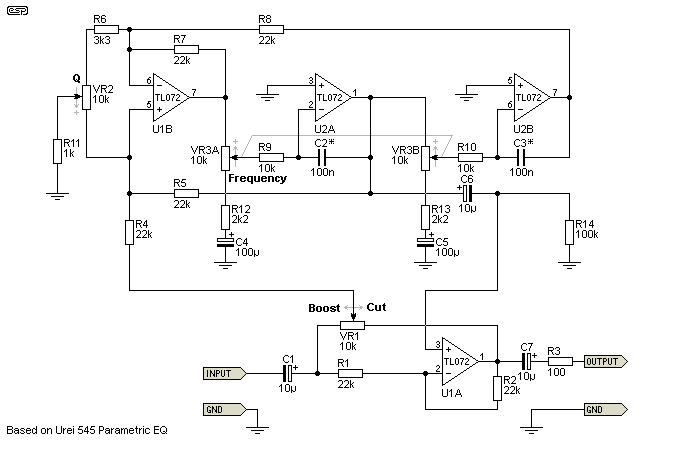
Figure 5 - Parametric Equaliser #2
The cut and boost control is implemented in the same way as #1, and most parametric EQ systems using this method simply cascade (connect one after another) as many stages as needed. While this inevitably adds noise to the signal, the signal itself will usually be at a reasonably high level so noise is not obtrusive. Sections that are not being used can be switched out of circuit to keep noise to a minimum.
There are other schemes that don't simply connect one stage after the next, but the circuitry is considerably more complex. Other common options are to provide switching to allow 'peaking' (as shown here) or 'shelving', where the output is taken from the low or high pass section instead of the bandpass. When this is done, it is usual for the Q/Bandwidth pot to be disabled, and in some cases the entire filter may be modified by switching to alter the phase response. If this isn't done, the circuit behaviour may not be as expected. In some cases, it may be necessary to use a separate high and low pass shelving equalisation section because the scheme shown cannot accommodate the required response. For those who don't know the term, shelving EQ is similar to that used in conventional tone controls, but in a parametric EQ the frequency is adjustable (see Project 28 'quasi-parametric equaliser' as an example).
As shown in the circuit diagram, the filter's centre frequency range is variable from 24Hz to 160Hz, and the bandwidth is variable from 2.7 octaves to a bit over 1/6th octave (Q of 0.46 - 8.2). Reducing C2 and C3 to 22nF raises the frequency range to 110 - 725Hz.

Both of the parametric EQ circuits shown use a voltage divider to set the frequency below the maximum (when the pot is fully clockwise and minimum resistance). At intermediate or minimum setting (minimum frequency), the frequency is not directly related to the pot's resistance, but by the voltage division ratio. It is a convoluted process to calculate the effective pot resistance, but for the Figure 5 circuit it works out to be about 55.3k. This is in series with R9 and R10, giving a total effective resistance of 65.3k, and that sets the low frequency to 24.37Hz.
I wasn't going to attempt to provide a formula, but it turns out that it's less complex than I expected. To work out the lower frequency (using the values shown in Figure 5), you need to calculate the effective pot resistance with the pot set to minimum (fully anti-clockwise) ...
EEff = 10k × ( 10k / 2.2k + 1 )
EEff = 10k × 5.54 = 55.54k ( + R9 or R10)
EEff = 65.54k
If you calculate the frequency using this value, it works out to be 24.31Hz. The advantage of using the pots as voltage dividers is that it allows the full frequency range to be spread out more effectively than simply using series pots. A series pot tends to cramp the higher frequencies into a narrow range, making frequency setting harder. The voltage divider doesn't cure this completely, but it works better than a series pot. It also keeps internal resistances lower, reducing resistor noise.
The formula provided can (with some manipulation) be used to determine the effective resistance at any intermediate pot setting. I leave this as an exercise for the reader.
As noted earlier, the state-variable is one of the most flexible topologies known. While the 'standard' version uses three opamps, there's another version that uses four. This lets you get four different responses simultaneously, and can be configured for variable Q without altering the passband gain. An example circuit is shown below, and it's not particularly complex compared to the basic version shown in Figure 1, but it doesn't need an extra opamp to obtain the notch.
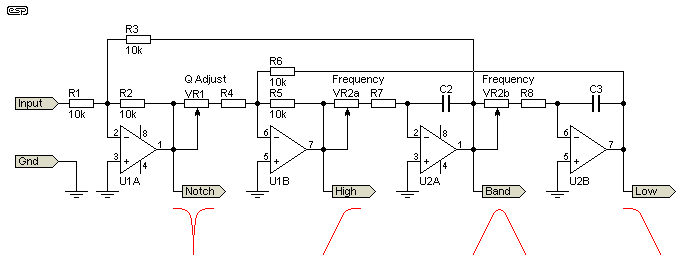
Figure 6 - Four-Opamp State Variable Filter
This is a re-arrangement of the 4-opamp version shown in AN1762 [ 6, 7, 8 ]. The addition of the fourth opamp allows the Q to be adjusted without altering the gain, and while that is also possible with the 'standard' 3-opamp version, it's not as good. However, the version shown still has some amplitude variation, but it's well controlled and with a Q of 0.707 (damping = 1.414) produces a maximum of only 3dB gain, but only for the low-pass and high-pass outputs.
If VR1 + R4 equals 7.07k, the filter is Butterworth (maximally flat amplitude). Increasing the value of VR1 increases the Q, and it can be made very high if required. Mostly, I'd suggest that VR1 would be perhaps 100k, which will provide a Q of 10. More can be had, but it's unlikely to be useful. Frequency is determined in exactly the same way as any other state-variable filter, and is determined by VR2a, R7, C1 and VR2b, R8, C2. Note that you may need to add a small capacitance (~10-22pF) in parallel with R6 if you use fast opamps. This will prevent possible oscillation.

Figure 7 - Four-Opamp Filter Response (Q = 0.707)
The response shown is obtained when VR2a+R7 = VR2b+R8 = 10k, and C1, C2 are 10nF. The centre frequency is 1.59kHz. Q is 0.707, obtained by setting VR1+R4 to 7.07k. As the Q is increased, the peak of the bandpass section remains at 0dB, as does the 'baseline' level from the notch section. The low and high pass sections show no boost (above 0dB) before rolling off (at 12dB/ octave) with high Q. The Q can be made 0.5 (Linkwitz-Riley alignment) with VR1+R4 set to 5k. The passband gain for high and low pass sections is then 6dB. At any setting, the peak amplitude of the bandpass filter is always unity gain (0dB).
Varying the value of R1 changes the gain, but doesn't affect the Q or frequency. To ensure nominal unity gain, the input should be driven from a unity-gain buffer so the external circuit doesn't affect the circuit gain. This isn't necessary if you want to change the gain of course.
As noted above, the state-variable filter makes an excellent notch filter by summing the high and low pass outputs. It is easily tuned, and the Q is adjustable so the width of the notch can be varied. Notch filters are used to remove single frequency tones (such as 50/60Hz hum) from an audio signal, or for distortion measurements. In both cases, it's much easier to start with a broad notch and then make it narrower by increasing the Q once it is properly tuned.
As with any notch filter, there is no theoretical limit to the depth of the attenuation of the tuned frequency. In reality, there will be frequency drifts and component drifts within the notch filter itself that make extreme rejection (more than perhaps 60-70dB) very difficult. A frequency change in either the oscillator or notch filter of only about 1Hz in 1kHz will cause notch depth to be reduced by more than 20dB with a Q of only 1. As Q is increased, the problem gets progressively worse.
Another use is to use the bandpass output, which can allow you to build a manual spectrum analyser [ 3 ]. The likely usefulness of such a device has diminished somewhat because of the ready availability of spectrum analysis software that runs on any PC, but when the referenced article was written (1982) such things didn't exist. No other filter design allows the level of flexibility that you can get from the state-variable design.
One of the other nice things about the state-variable filter is that it can be used anywhere a more 'traditional' Sallen-Key or multiple feedback filter can be used. The demands on the opamps are generally much lower than other topologies, so quite pedestrian opamps will work much better than expected. This is particularly true of the integrators, as they are relatively slow-acting by definition. The first stage may need to be faster than expected if high Q values are used at high frequencies.
Texas Instruments makes a dedicated state-variable filter IC, the UAF42. This has two integrators, the adder/ subtractor first stage opamp and an extra non-committed opamp that can be used as an input buffer, inverter or whatever you might need it for. Unfortunately, it is stupidly expensive so it's much cheaper to use conventional opamps.
Voltage controlled state-variable filters are common in synthesisers, and the way most are configured is to use an operational transconductance amplifier (OTA) in place of the resistors that feed the two integrators. These specialised opamps have an output current that is determined by the input voltage and control current. While I do not propose to cover these in any detail, there are plenty of examples on the Net. Unfortunately, OTAs are now obsolete, and no-one makes them any more. Of course, you can try your luck on eBay - you may even be lucky enough to get one that works! (But don't count on it.)
In short, state-variable filters can be used anywhere you might use a traditional Sallen-Key or multiple feedback design, and preferably where the filter slope doesn't need to be greater than 12dB/ octave. High Q (narrow bandwidth) peak and notch filters are available. The bandpass filter has an ultimate rolloff slope of 6dB/ octave, in common with the multiple feedback design. The advantage is that higher Q can be used without having to use very fast opamps - even at relatively high frequencies. This is so because the state-variable design doesn't require the high gain needed by many other designs when high Q filters are needed.
There are better alternatives if you need only a bandpass filter. A very good example is shown in Project 218. The filter is based on a 'generalised impedance converter' (GIC), and requires two opamps. It's capable of very high Q, and is easily tuned. A state-variable filter can certainly achieve the same result, but it's more complex overall, and is also harder to tune, and getting the optimum balance of Q and gain isn't straightforward.
As has been described here, the state-variable filter is one of the most versatile filter blocks available. Despite its requirement for more opamps than other filter types, there are many mitigating factors that make it worthwhile. A second order filter is easily tuned simply by varying two resistors, and a reasonably inexpensive dual-gang linear pot is usually able to tune the filters with only minor changes to the signal amplitude or filter Q. Given the circuit's capabilities, the addition of a couple of additional opamps isn't a high price to pay for the performance.
The unique capabilities of this class of filter are not shared by any other - in particular the ability to have high, low and band pass outputs from the same filter, always with the same phase relationship. This even applies if the tuning pot doesn't track very well, although filter Q may be significantly affected if tracking is not accurate. However, it must be remembered that the high-pass and low-pass sections are always subjected to a 180° phase shift. One or the other needs an inverting buffer when used as a crossover network for example.
With the very modest prices for even surprisingly good opamps these days, there is a lot of opportunity for the adventurous electronics enthusiast to experiment with these filters. Just building one and playing with tuning and Q will convince you of the benefits. That's exactly what I did when I first found out about the state-variable topology, and I'm still using my lab amp with its state variable crossovers to this day. Having been built in the late 1970s, that means I've been using it for over well 40 years!
 Main Index
Main Index
 Articles Index
Articles Index