

|
| Elliott Sound Products | Negative Impedance |
 Main Index Main Index
 Articles Index Articles Index
|
Negative impedance (or resistance) is a rather odd concept, and it seems unlikely (impossible, even) when it's first mentioned to most people. However, there are some fairly common parts that exhibit negative resistance, albeit only over a limited range of operation. One of these is the humble neon lamp. When voltage is slowly applied, initially there is no conduction. When the voltage reaches around 70-90V (depending on the lamp), it suddenly conducts. There is then a region of negative resistance, where the voltage across the lamp falls, but the current goes up.
By definition, that is negative resistance. With the resistors we all know and love, their characteristic is positive resistance, so as the voltage rises or falls, the current rises or falls in direct proportion to the voltage change. Everyone in electronics knows Ohm's law, and it is (or should be) embedded permanently in one's subconscious for recall at a moment's notice ...
R = V / I Where (of course) R is resistance, V is voltage, and I is current
There are several articles on the ESP site that look at negative impedance, and they are listed in the references section. There will be further references to parts of these articles throughout this text, because it was the concepts discussed that prompted a separate article to look at negative impedance more closely. There are some rather bizarre aspects to any negative impedance device, and this is especially true when theoretically 'ideal' negative resistances are looked at. Somewhat surprisingly perhaps, a NIC (negative impedance converter) based on opamps can approach the theoretical model, at least at low frequencies where the opamp has maximum gain - typically in excess of 100,000 (100dB).
For the remainder of this article, the term 'NIC' will be mostly used in place of 'negative resistance', 'negative impedance' or 'negative impedance converter'. Naturally, there will be exceptions, depending on the context. While I use the term 'impedance' most of the time, this can often be just simple resistance (no frequency dependency as the word 'impedance' implies).
Note too that there won't be an attempt to cover every different type of NIC, as there are just too many. I will concentrate on those that are interesting (or that I think are interesting), and I'll show as many examples as I can. Where possible, they will also be explained - necessary because negative impedance is not intuitive.
It's fair to say that some of the examples won't have a practical use, at least as shown. However, most are actually potentially worthwhile, and if nothing else they can be great fun to play around with. Simple opamp based NICs are easy to build so you can prove to yourself that negative impedance exists, and you may even see a use for one in your next project. However, this is probably unlikely, but one never knows. 
Most of the circuits shown expect to be fed from a low impedance source, which in all cases must be earth (ground) referenced. Opamp power connections are not shown, nor are supply bypass capacitors or pin numbers. There is no guarantee that all circuits are functional as shown. Opamp power is not shown, but dual supplies (±5-15V) are required unless otherwise noted.
It's important to understand that any NIC can only ever be conditionally stable, meaning that some combinations may not work as expected unless all operating conditions are satisfied. We are used to opamps that are unconditionally stable, meaning that they will never oscillate or lock-up under normal linear operating conditions. This is provided that all datasheet conditions are met of course, including proper PCB layout, supply bypassing and component values that ensure that all voltages and currents are within specification.
In contrast, a NIC can become unstable or lock-up (e.g. switch to one supply rail or the other) or become 'dysfunctional' for any number of reasons. Component tolerances are usually far more critical than with conventional linear circuits. While a resistor or capacitor tolerance of ±10% will do no more than change the gain or frequency of a conventional circuit, that same tolerance may make the difference between a negative impedance circuit working or producing an epic fail.
In this article, reference to 'audio frequencies' doesn't necessarily mean audio or hi-fi, but simply means a circuit is usable at frequencies from a few Hertz up to perhaps 30kHz or so. Many industrial processes also work within the audio frequency range, but they are not used for speech or music. It's an important distinction, and it applies across many fields of electronics.
Although I've already described it, there are some things that you need to understand about negative impedance. As its name suggests, it can be used to make 'real' resistance simply 'disappear'. For example, if you have a signal generator with zero ohms output impedance, a load that's exactly 100 ohms, and you feed it with an impedance that's exactly -100 ohms, there is no resistance. None at all. This is identical to a short circuit, but the voltage developed across your 100 ohm load will be infinite, as will the current through it. This rather nonsensical situation cannot occur in real life for a variety of reasons.
It's is not possible in an opamp (or even a power amp) based circuit, because they will always have a defined supply voltage (which limits the amplitude) and the output can only deliver the current that the device can provide (typically ±25mA or so peak current for an opamp). All real life sources have a finite (positive) impedance and/ or voltage and current limits. Few signal generators have an output impedance of less than 50 ohms, so you'll never normally see anything even approaching infinity.
Negative impedance is fundamentally weird, and a NIC behaves in what may seem to be incomprehensible ways until you examine it closely. If you have a simulation package on your PC, it may be possible to simply tell it that a resistor has a resistance of -100 ohms - an instant negative impedance, and you don't even have to build much of a schematic. I use SIMetrix [ 9 ], which is perfectly happy for you to do that. Other simulators may or may not behave the same way.
The question is how and why your load resistor can be made to 'disappear'? If the +100 ohms (your load) and the -100 ohms (negative resistance) cancel, the whole circuit must be a short circuit. In order for it to appear to be a short circuit to the signal generator (assuming zero ohms impedance), it must draw infinite current. That means an infinite voltage across the -100 ohm resistor, and an infinite (but opposite polarity) voltage across your +100 ohm load. The two cancel, and the signal generator simply sees a short circuit. In the following drawing, the generator has an internal resistance of 50 ohms - this removes the requirement for infinite voltage and current because it limits the current to a sensible (and achievable) level.
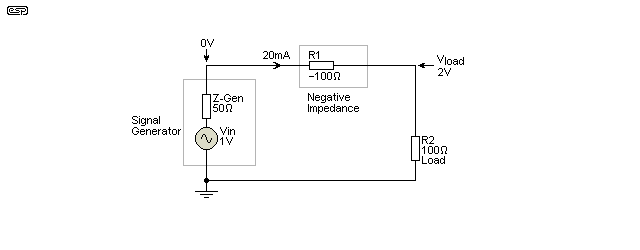
Figure 1 - Negative Impedance Concept
Basic laws of physics (Ohm's law in this case) show what must happen in the circuit. The two external resistances cancel perfectly, so the generator sees a short circuit at the output. There's zero voltage, but a current of 20mA flows through R1 and R2, limited by ZGen, the signal generator's internal impedance (1V with 50Ω in series). Therefore, the voltage across R1 (negative resistance) must be -2V, with +2V across R2 (the load). It doesn't matter if the voltages are AC or DC, but of course with AC, the voltage across the negative resistance must have its phase reversed so the two voltages cancel out. The result is a short circuit at the generator terminals, and R2 (the load resistance) has effectively 'disappeared'. Note that 'disappear' is in quotes because it's only an apparent disappearance - the resistance is still there, but its influence is removed by the NIC.
When you make any calculations, all resistances must be considered, including the generator's output impedance. I encourage you to do some sample calculations so that the currents and voltages can be determined for different resistances, as that will help you to understand how it all joins up.
I = V / R ('R' is the total resistance, positive and negative, and including the resistance of the generator)
R = -100Ω (R1) + 100Ω (R2, Load) + 50Ω (ZGen) = 50Ω
I = 1 / 50Ω = 20mA
VLoad = R2 × I
VLoad = 100Ω × 20mA = 2V
While the concept may seem odd, it all works out easily. We'll again assume a voltage of 1V (it doesn't matter if it's AC or DC), and see what happens when the load resistance is reduced to 40 ohms. If you don't run through a few simple calculations it won't make much sense, so it's well worthwhile to spend a few minutes.
I = V / R ('R' is the same as above)
R = -100Ω + 50Ω + 40Ω = -10Ω
I = 1 / -10Ω = -100mA
VLoad = R × I = 40Ω × -100mA = -4V
This shows how (and why) the polarity reverses (or an AC signal is 180° out of phase) when the negative resistance is greater than the total 'real' resistance. Whether you calculate this or run a simulation, you will get exactly the same results. The same formulae work for any combination of voltage, 'real' resistance and negative resistance. As you can see, nothing more involved than Ohm's law is needed for complete analysis.
Making a simple NIC using an opamp works rather well. One of the first things you will find is that the absolute value of the load vs. the negative impedance is important. As seen above, for a negative resistance/ impedance to work in the manner you expect, the value of the negative impedance must be lower than the actual (positive) impedance. It the negative resistance is (say) -100 ohms, then the total positive resistance will usually be greater than +100 ohms. Once the positive resistance is less than 100 ohms, the negative resistance becomes the dominant part of the equation, and the signal polarity is inverted as shown in the calculation above.
There are a few common devices that exhibit negative impedance - at least over a limited range. A neon lamp is one of the easiest to analyse and experiment with, because the voltage is passably safe (less than 100V), and it's easy to build a simple relaxation oscillator using nothing more than a neon lamp, a resistor and a capacitor. If you try to do the same thing with something that does not have a negative resistance region, all you get is a steady DC voltage. The negative impedance region means that it becomes an oscillator.
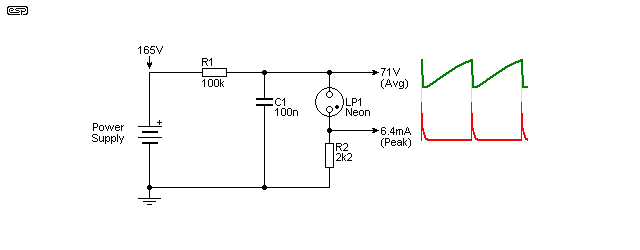
Figure 2 - Neon Lamp Relaxation Oscillator
When the voltage is below the neon's strike voltage, no current is drawn. Once the lamp 'strikes' the neon gas ionises, and the negative impedance causes the voltage across the neon to fall as the current through it rises. This is known as the Pearson-Anson effect [ 4 ]. The capacitor will be discharged until the voltage across the neon lamp is insufficient to maintain ionisation, the lamp then extinguishes and the cycle repeats. The resistor must be a fairly high value, or it may be able to provide enough current to maintain ionisation within the lamp, and the circuit won't oscillate. The oscillator circuit shown will stop oscillating when the supply voltage is a little over 260V (a continuous current of around 1.9mA). Changing the voltage also changes the frequency, but the output amplitude is not affected.
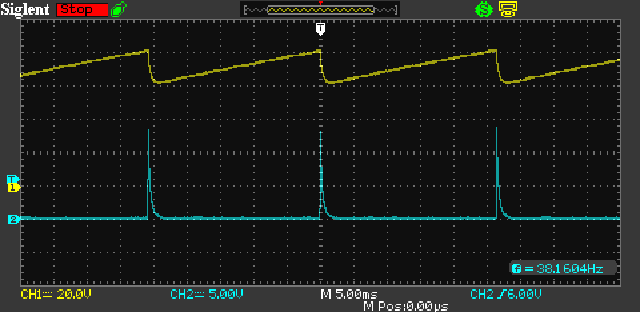
Figure 3 - Neon Lamp Oscillator Waveforms
As you can see, the waveforms are pretty much what you'd expect. The average voltage across the neon measured 71V, and the neon strikes at about 81V and extinguishes at 61V (the sawtooth output is 20V peak to peak around the 71V average). Peak current is monitored across the 2.2k resistor, and measures 14 volts, so the peak current is 6.4mA with a total duration of only 2ms. The negative resistance of a neon lamp is not great, and there is a significant positive resistance as well. However, if the negative resistance region didn't exist the circuit could not oscillate.
As an aside (since it has little to do with the main topic here), neon lamp oscillators have been used as frequency dividers, and were used in some early electric/ electronic organs. The frequency was set to be a little lower than half the input frequency, and the discharge spike from the previous divider triggered the neon to fire at each second input pulse. This divided the frequency by two (one octave). A typical organ using this type of divider needed a great many neon lamps, and the supply was regulated to ensure stable operation.
All gas discharge lamps exhibit the same general characteristic of negative impedance. While you could also build an oscillator with a full sized fluorescent tube, it would be somewhat unwieldy due to the size of the tube. It would also require a dangerously high voltage to cause ionisation, so it's not a recommended DIY project  . All gas discharge lamps have a negative resistance region, but the small neon is really the only one that's useful for the experimenter.
. All gas discharge lamps have a negative resistance region, but the small neon is really the only one that's useful for the experimenter.
Another negative impedance device that used to be reasonably common was the tunnel diode. These are now very hard to get, as are Gunn and IMPATT (IMPact ionisation Avalanche Transit-Time) diodes which also have a negative impedance region. The various negative impedance diodes mentioned are used at microwave frequencies, but will not be covered here.
A DIAC is another negative impedance device, and they are common in TRIAC lamp dimmer circuits. An example circuit is shown in Project 159 (Leading Edge Dimmer, Figure 6). DIACs are classified as bidirectional trigger diodes, with a breakdown voltage between ~28V and 45V. These will also oscillate with a parallel cap and series resistor. A DIAC oscillator uses same basic circuit as a neon oscillator, but with lower voltage. These devices remain readily available at low cost, but the requirement for them is now somewhat diminished.
Another of the better known negative impedance semiconductors is the unijunction transistor (UJT), such as the 2N4871 (now discontinued). A variant is the PUT (programmable unijunction transistor) such as the 2N6027 and 2N6028 (also discontinued). As you can see, there's a pattern here, with many of the negative impedance devices being no longer available - at least from major suppliers. You can probably get them from ebay or other suppliers, but you might not end up with what you wanted and paid for.
Most of the tasks that used to be performed by UJTs and PUTs are now done with timers such as the 555, or by means of a microcontroller. They were always something of a niche product, and an unkind person might even suggest they were a solution looking for a problem. To some extent that was always true, because their uses were somewhat limited, as they were used primarily for simple oscillators that didn't need great accuracy or stability. There aren't many applications that can't be done with more 'conventional' parts, and the need for esoteric negative resistance parts is minimal.
The circuits described in this section are all non-linear, and aren't suitable for any kind of signal processing. For that we need to become more adventurous, and look at linear negative impedance circuits. There are several different types, with some being pretty much purely theoretical (i.e. they don't do anything useful) and others being used in advanced circuitry. They remain relatively uncommon though, but may be hidden inside ICs designed for high-performance filters (for example).
There are several circuits that can be used to make a basic NIC, and building one with an opamp and a few resistors is quite simple. One characteristic that is shared by all NIC circuits is positive feedback, which has to be tightly controlled or the circuit will oscillate. That means that using a NIC to drive any load that is unpredictable (e.g. anything that can be changed or altered by the user) is unwise. As noted in the ESP article Effects Of Source Impedance on Loudspeakers, using negative impedance for any loudspeaker is probably a bad idea. In theory there appear to be advantages, but in reality this rarely turns out to be the case.
One area where negative impedance really does work is explained in Transformers For Small Signal Audio. That article also shows oscilloscope captures of the waveforms expected in use. Using a NIC to drive an audio transformer means that the primary winding resistance can be (at least partially) cancelled out, allowing higher output levels, lower distortion and improved response at low frequencies. C2 is an absolute requirement, which is unfortunate but unavoidable.
With C2 shorted out, the circuit has extremely high gain at DC and may easily become unstable. If C2 is there, it causes the response to rise at very low frequencies. A NIC transformer driver should always be preceded by a high pass filter to remove infrasonic energy. C1 goes a small way towards fixing this problem, but it's not a complete cure. The simple act of starting and/ or stopping a signal creates an infrasonic 'disturbance', and the NIC makes it worse than conventional voltage drive. With the values shown (and a similar transformer), response is less than 1dB down at 10Hz.
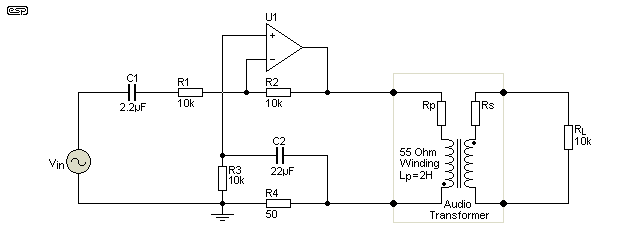
Figure 4 - NIC Used To Drive An Audio Transformer
The NIC is based on U1, which can be any normal opamp, a pair of paralleled opamps (for improved drive current), or an opamp with a buffer to allow it to drive a lower impedance. The output impedance is set by R4, and is 50 ohms to suit this transformer. You must determine the correct value for the transformer you want to use, with a value that's a little less than the winding resistance. When the opamp is attempting to remove distortion caused by partial saturation, the output current may be much higher than you anticipate.
Note: Be very careful with this arrangement. It works exactly as claimed, but the negative impedance set by R4 must be less than the primary winding resistance. If you use more negative impedance, the circuit will oscillate at a low frequency, determined (at least in part) by the inductance of the transformer. If you rely on a simulator, you can easily be lulled into a false sense of security.
C2 and R3 are used to ensure that the circuit has unity gain at DC, and without them the DC conditions in the circuit are seriously unpredictable. By using this arrangement, the output impedance is reduced because the transformer's primary resistance is (mostly) cancelled out. This also means that the circuit will 'automatically' pre-distort the input signal to compensate for transformer distortion caused by partial saturation of the magnetic core.
The transformer is wired with the secondary reversed, because the NIC is inverting. You also need to be aware that you 'lose' more than half the available output from the driving opamp, some across the resistor (R4) and some because the opamp needs headroom so it can 'pre-distort' the signal to produce a clean transformer output. This is unlikely to be an issue, because the small, cheap transformers that need this technique most usually can't handle more than around 1V RMS anyway. This limit is at low frequencies, typically 40-50Hz (transformer dependent of course), and is due to core saturation.
Notwithstanding the warnings, and as unlikely as it may seem, negative impedance drive works very well. The reason is superficially complex, but it's actually quite simple. A transformer with no winding resistance and driven by a pure voltage source (i.e. zero ohms) has no distortion. Saturation distortion occurs because the transformer draws high non-linear current as the core starts to saturate, and this distorts the voltage waveform across the primary due to the winding resistance. When a NIC is used to drive the transformer, the winding resistance can be cancelled, so the transformer appears to be driven from an almost 'perfect' voltage source. It is inadvisable to try to cancel all of the winding resistance, because a small variation in the actual resistance will make the system unstable. As seen above, the NIC provides a -50 ohm output impedance, driving a 55 ohm winding. The effective impedance across the primary is therefore only 5 ohms, instead of 55 ohms.
This is stable, but we also need to ensure that extremely high gain is not available at DC, hence the addition of C2 and R3. The resulting 5 ohms of effective winding resistance means that the saturation distortion is almost completely cancelled - at least up to the point where the driving opamp runs out of voltage or current. In addition, the low frequency response is extended, but again, this is restricted by the opamp's output voltage and current limits.
At frequencies well above those that cause saturation, the opamp does not see a very low impedance. It sees the (transformed) impedance presented to the secondary of the transformer, plus the secondary winding resistance. In the above (and assuming an ideal (non-saturating) transformer, the peak current is developed at around 6Hz, where the NIC is compensating for the small inductance of the transformer (2 Henrys as shown). With a 1V input, the maximum current is 10mA, but this is overcome by including a high-pass filter that restricts the response to perhaps 15Hz and above.
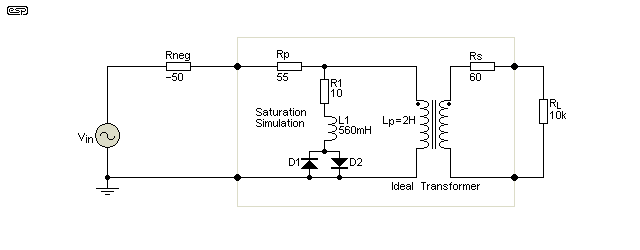
Figure 5 - Saturating Transformer Test Circuit
Real transformers saturate, and most simulators don't do a particularly good job of showing the waveforms you get when a transformer approaches saturation. Figure 5 is an attempt to demonstrate the effect, and it works reasonably well, at least to the extent that it can prove the point. At high frequencies (1kHz and above), distortion is minimal with or without the negative impedance drive. With an input of a little over 3V peak at 44Hz, the distortion when driven from a voltage source is 7.4%, which falls to 0.14% when the NIC is used. With negative impedance drive, the transformer's output voltage is also higher, and low frequency response is extended.
In the article Transformers For Small Signal Audio, there are waveforms captured from a real transformer as it's driven towards saturation. The test circuit above only goes part-way towards the simulation of saturation, but it doesn't produce the actual voltage or current waveforms that exist in a physical transformer. The ability of the NIC to minimise the distortion is just as real though.
There is one very common NIC that's used in several 'explanations' found on the Net. While it certainly does what a NIC should do, it's actually not a particularly useful arrangement in the form shown. The point marked '-Z' shows where the negative impedance is found, and the value is equal to R1. If Rin is made to be 900 ohms, a 1V (peak) input signal (AC or DC) will be inverted, and a voltage of -10V (or 10V AC with inverted polarity) is seen at the opamp's input. The current from the generator is determined by the difference between +900Ω and -1k, or -100 ohms. Therefore, a 1V DC input will pass -10mA ( I = V / R ), and not +1.11mA as would be the case if the input resistor (Rin) were returned to earth/ ground rather then the NIC input.
There are several (often wild) claims made about the circuit, including that you can substitute capacitance or inductance for any or all of the resistors (impedances) shown. This allegedly means that you can make a negative capacitor (an inductor) for example, but don't expect some of the published circuits to actually work with real opamps. This circuit is of minor interest only as an analogue 'building block', and has been included here only because it's so common on the Net.
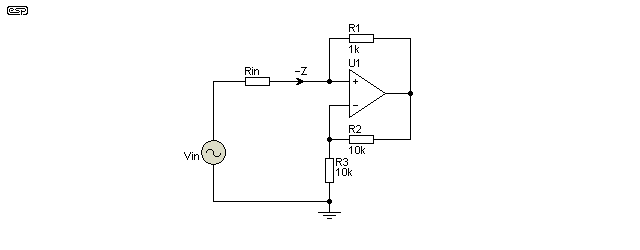
Figure 6 - Common NIC Used For Explanations
This NIC is often shown with a voltage input, which is the basis for most explanations. In real life, the input will normally be a current, and applying a voltage (from a low impedance source) doesn't achieve anything you can work with so easily. However, as a first analysis it's helpful to see what happens. Note that the voltage source must have a very low output impedance, or the basic analysis doesn't work.
Let's assume an input voltage of +1V, applied directly to the input of the NIC (resistor Rin shorted). Since the impedance is negative, we expect -1mA to flow from the signal source, not the +1mA we'd get from a 'normal' resistor. The opamp has a gain of two, set by R2 and R3. That means that the opamp's output pin sits at +2V (remember there's +1V input, and the opamp is non-inverting). Therefore, a current of 1mA flows through R1 - back to the voltage source !. A meter will show a current flow of -1mA into the NIC, but would show +1mA into a normal resistor.
Now let's assume an input current of 1mA, created from 1V input, passed through a 1k resistor (Rin). The NIC has an impedance of -1k, so the two resistances will cancel. That means that the voltage source that should be supplying 1mA sees a dead short circuit, because the two resistances completely cancel. This assumes that the opamp used for the NIC is capable of infinite current, derived from an infinite supply voltage. Unfortunately, these are hard to come by.
I suggested an input resistance of 900 ohms in the first place, because that lets you analyse the circuit easily. The process of analysis doesn't need any maths, apart from addition, subtraction and Ohm's law. It's too easy to completely mess up people's understanding by supplying formulae to try to 'simplify' the explanation. It's worth noting that although the circuit shown is a very common example, it's not actually useful in this form. For example, it will not work driving a transformer (as shown above), and with no input connected, it will swing straight to one supply rail (polarity depends on the opamp used).
The only way you will understand this circuit is by running simple calculations, or by building one to see what it can do. When an input resistance is used, things can go pear-shaped very quickly if you aren't aware of what's happening. However, building one may be seen as a fool's errand, because it's usefulness is so limited. It's important to understand that the negative impedance must never be 'dominant', as that means the circuit has more positive feedback than negative.
The last sentence above is one thing that's never mentioned with this circuit, which is a shame, because it's seriously important. The value of input resistance (Rin) must always be less than the negative resistance (R1). As the values converge, the gain of the circuit climbs rapidly until the opamp clips, because it can't produce the infinite voltage and current needed to completely cancel the external positive resistance. When the positive impedance is greater than the negative resistance, you have a Schmitt trigger (sometimes referred to as a 'regenerative comparator'). This does not happen with a simulated 'ideal' opamp, but on the test bench there is no question as to what works and what does not. Simulating with an opamp model produces the same result as the test bench.
I don't recall where the next circuit came from, and an extensive search failed to find it again. Hence, there is no reference for it. By using negative impedance, the circuit's Q (quality factor) can be much higher than can easily be obtained from a multiple feedback (MFB) bandpass filter. It has the advantage that the opamp doesn't require a large gain-bandwidth product, but it's more complex than the MFB filter. Because it's such a bizarre idea, I ran a bench test to check whether it really works, and the answer is a qualified "yes". More on this below.
The output is high impedance, and needs to use a follower (U2) to ensure the second filter (Rt2 and Ct2) isn't loaded down as this will both change the frequency and reduce the filter's Q. There are effectively two separate filters, with Rt1 and Ct1 forming a high pass section, and Rt2 and Ct2 forming the low pass. Without the NIC, this circuit would have a Q of 0.5 (same as a Wien bridge) but the application of negative impedance changes this completely. The combination of a series and parallel RC network is the same as you find in a Wien bridge, but in this version, the NIC is between the two networks.
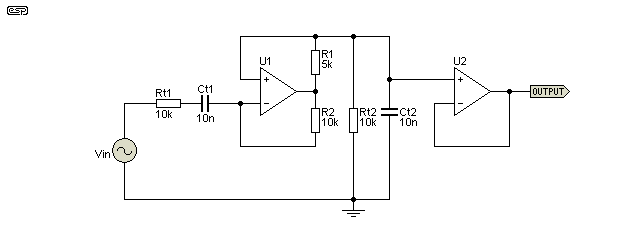
Figure 7 - Negative Impedance Bandpass Filter
When the ratio of R1 and R2 is exactly 1:2 the negative impedance is equal to the impedance of the two RC networks, and the input sees a short circuit so the opamp is expected to provide an infinite current. Naturally, this cannot occur, and even 1% resistor tolerance is enough to reduce the Q of the filter dramatically. In theory, a Q of over 1,000 is possible, but the circuit will be unstable and unusable, and it will simply oscillate. This is tempered somewhat by making R1 5.1k, reducing the Q to around 24. This is still a high Q filter.
Note that for stability, R1 must be greater than half the value of R2, assuming Rt1 and Rt2 are identical, and likewise Ct1 and Ct2. This is affected by the respective tolerance of the frequency determining parts, and these can (and do!) reverse the way R1 works. For example, if Rt1 happens to be a little smaller than Rt2, then R1 must be less than R2/2 and vice versa. The tolerances are small, and for high Q there is very little room for error.
While this circuit simulates (and works in my test setup) perfectly, it may not work unless you get everything right. It's also important to realise that very high Q filters can take a long time before the output stabilises. When the output has reached its final amplitude, it's said to be operating with 'steady state' conditions. The time for a signal to reach full amplitude with a high Q resonant filter can be much slower than expected. A filter with a Q of 30 will take about 100ms to reach the steady state maximum. When the signal is stopped, it takes a similar amount of time for the signal to decay back to zero. Very high Q filters are never used in audio, but are fairly common in other applications, such as test and measurement (T&M). Unless you have a specialised application, you will never need this filter.
Because this is such an odd circuit and it probably shouldn't work, I had to put one together to see what it could do. The result is shown below, with a tone burst signal (150 cycles on and 150 cycles off). To be able to obtain very high Q, resistors and capacitors need to be better than 0.1% tolerance, and a very small change in the wrong direction will change a filter into an oscillator.
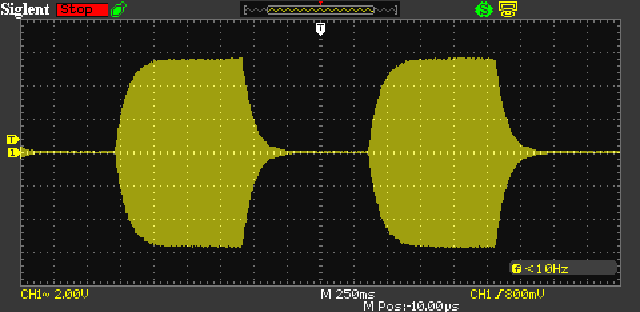
Figure 8 - Negative Impedance Bandpass Filter Response
The tone burst response of the NIC based bandpass filter is shown above. It was operated with a Q of just under 40, at a tuned frequency of 158Hz (100nF and 10k, ± component tolerance). No attempt was made to match the components, but I was able to get a Q of 80 (that's very high - it means a bandwidth of just 2Hz for a 158Hz filter). Any attempt to increase the Q further and it oscillates. The output is 5.8V peak (4.1V RMS) with an input of 57mV peak (40mV RMS) - a gain of 100 (near enough).
A resistance change (of R1) of only 24 ohms (for a nominal 5k resistor) changed the Q from 40 to 80. From that it's apparent that component sensitivity is very high with high Q. As you can see, with a Q of 40, it takes a little over 250ms (1 division plus a bit) for the signal to build up to the maximum, and the same to fall to zero. This is not a limitation of this particular circuit - it applies to all high Q filters.
As an oscillator, you might imagine that it's a fairly simple arrangement that should perform well. However, distortion performance is very ordinary, and when set up for reliable oscillation, expect it to be around 3% THD. This can be improved, but not without a thermistor or other form of gain control element. For a range of oscillators (not including this one), see Sinewave Oscillators - Characteristics, Topologies and Examples.
There are several other rather complex negative impedance circuits that are sometimes used to create very sharp filter slopes. One of these is the 'GIC', covered next.
The GIC (generalised impedance converter) is also known as an FDNR, or frequency dependent negative resistance [ 6 ]. These are probably one of the least common filter topologies, but they are used mainly for specialised requirements. Sometimes I wonder if they are used just so people can show how clever they are (and working out one of these is not for the faint-hearted). So yes, the designers are clever, but it's rare that most users will ever need one. However, since we are looking at negative impedance it would be remiss of me not to mention these circuits. An example is shown below, a low pass filter tuned to 1,020Hz and with a 12dB/ octave rolloff.
R4 changes the circuit's total Q, which can be varied over a small range without substantially affecting the filter frequency. As shown, the filter is Butterworth (maximally flat amplitude). R2 and R3 only need to be the same value, and if both are changed operation is not affected. Perhaps surprisingly, C1 and C2 can also be changed to modify the Q, but both should be the same value. The frequency is largely determined by R1 and C3, but is √2 times the calculated frequency (at least for the example shown here). However, all values are inextricably linked, and the frequency can be changed by scaling capacitor values alone. For example, changing C1, C2 and C3 to 47nF reduces the frequency to 217Hz, but Q is unaffected.
I did warn you that this is a difficult circuit to analyse, and the guidelines above (and that's all they are) may help you towards some fruitful experiments. It may also be enough to scare you away, but I'm hopeful that someone will get something from my meagre efforts  .
.
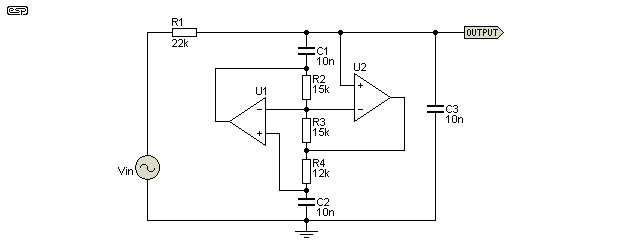
Figure 9 - Generalised Impedance Converter 2nd Order Filter
The GIC filter doesn't work any better than a Sallen-Key filter at audio frequencies, but needs an additional opamp and several more resistors. It also has a relatively high output impedance, so an output buffer is essential. The original idea was apparently to minimise the 'real world' limitations of opamps, but these days I doubt that there are too many good reasons to use a topology that is anything but intuitive. The impedance conversion is used to make capacitors act like inductors, in much the same way as a gyrator (covered next). The filter shown is (roughly) equivalent to an inductor-capacitor (LC) low pass filter, with the high Q inductor being synthesised by the GIC. This is one area where the GIC excels - making a simulated inductor with a very high Q, and without excessive loading on the opamps. That is something that's hard to do with 'ordinary' gyrators or simulated inductors.
The circuit shown above is for the sake of completeness, and a detailed analysis is not going to happen. If you think that this approach is the solution to your filtering woes, then feel free to look up more info on the Net. There's plenty to be had, but I leave it to the reader to search out if s/he wants to pursue this type of circuit. (Yes, I am faint-hearted when it comes to complex maths - I prefer the simplest solution wherever possible).
One of the main reasons that the GIC topology is used is when opamp bandwidth would otherwise compromise performance. This will usually become a problem when dealing with high frequency filters, where the GIC will (hopefully) provide better performance than more common filters (Sallen-Key, multiple feedback, etc.). These filters are complex though, and a deep understanding is necessary to make sense of what's going on.
The gyrator [ 7 ] is a common circuit, and isn't normally a negative impedance device in the true sense of the term. It's included here because it reverses the effects of reactive elements, so capacitors can be made to act as inductors and vice versa. There is rarely any need to convert inductance to capacitance, but if you really do want a particularly poor capacitor it's easily done. When reversing the action of a capacitor to create an 'inductor', the final circuit possesses all the things about inductors that make them the most flawed electronic part known. Adding a NIC changes things, but at the expense of added complexity which isn't warranted in most circuits.
Despite their shortcomings, even basic gyrators remain a useful tool in the electronic enthusiast's arsenal, because they are not affected by stray magnetic fields, and can easily be adjusted to an exact inductance. This is very hard to achieve with real inductors, which are also prone to saturation (if using a ferrite or iron core), and are usually far more expensive to produce than a simple opamp circuit. There's a complete article that looks at gyrators in general, but here we will only look at one that utilises negative impedance to remove the traditional gyrator limitations (winding resistance in particular).
The basic NIC gyrator is shown below. When fed with a signal, it behaves like an inductor in nearly all respects, except it has almost zero winding resistance. Just like a real inductor, it even provides a back-EMF when a DC input is disconnected, but the amplitude is limited to the opamp's supply voltage.
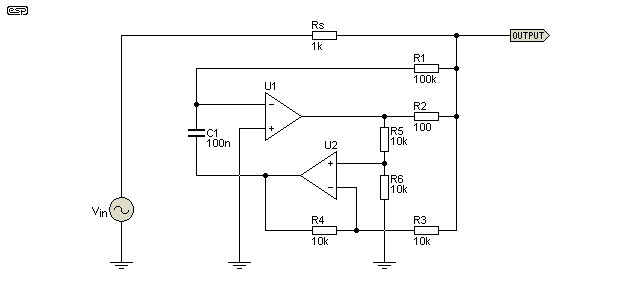
Figure 10 - NIC Gyrator
Inductance is determined by R1 × R2 × C1, and with the values shown it's 1 Henry. R3-R6 only need to be the same value, and the value used (10k) is a suggestion only. Adding the NIC to the gyrator increases the number of parts used, but performance is greatly improved. A traditional single opamp gyrator is hard pressed to minimise the effective winding resistance, but the NIC removes it almost entirely. The circuit is limited only by the opamp performance, but even fairly pedestrian opamps will perform surprisingly well.
The drawing above is by no means the only version that you'll see. The article on gyrators shows an alternative circuit, and they are often drawn to look like the GIC topology shown above. Not unreasonable, because that's essentially what it is - a GIC or FDNR. By using negative impedance, the otherwise (sometimes) troublesome equivalent of winding resistance can be eliminated. Most of the time, it's not necessary though.
NICs are (or have been) used in a number of seemingly odd applications. Bell Labs devised a technique in the 1940s where negative impedance amplifiers were used on long transmission lines as repeaters. A NIC provides a lower cost solution than a traditional repeater which requires a pair of 'hybrid' circuits (2 to 4-wire converters and 4 to 2-wire converters - see 2-4 Wire Converters / Hybrids) and two amplifiers. These were refined over the years, and there are many patents on the technique [ 8 ]. These will not be covered here, as the application is too specific to telephony, and isn't likely to be useful for general applications.
Similarly, negative impedance is sometimes used in antenna matching circuits, in order to correct for impedance differences between a transmission line and an antenna or amplifier. It can be very difficult to get any sensible information on some of the applications, because the information is hosted on sites that expect you to pay for it.
Patents can be a good source of information, but it's usually disclosed in 'patent speak' which is not always intelligible unless you are a patent attorney. An example is shown below, [ 10 ] from a patent granted in 1958. It is described as a "Negative-Impedance Transistor Oscillator". For its day I have no doubt it was novel, but likely with somewhat limited application. Stability is poor, but it is interesting enough to show here.
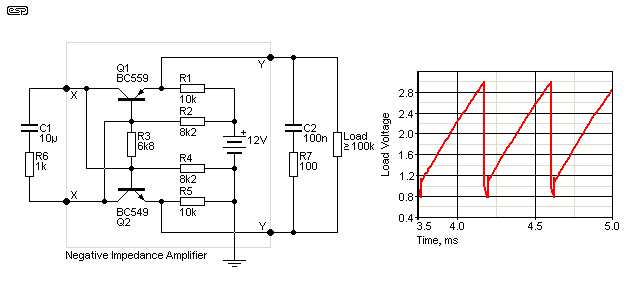
Figure 11 - Negative Impedance Transistor Oscillator
The circuit has been simulated (no, I'm not going to bother building one), and it appears to work. The output waveform (across the load resistor) is shown. It oscillates at 2.3kHz with the values shown, which bares no relationship to the tuning components (C2 and R7). According to the patent information, the points marked 'X' are 'short circuit stable' ports, but the amplifier module is unstable if they are left open. The points marked 'Y' are the opposite. The network across the 'X' points was shown in the patent drawings, but the circuit works without it. If you are interested, it's worthwhile re-drawing the circuit. You'll find that it's rather similar to the transistor equivalent of a silicon controlled rectifier (SCR).
In operation, C2 charges from the amplifier, and when a critical (trigger) voltage is reached, the transistors conduct with an effective negative impedance. This discharges C2 very quickly, and the cycle repeats. The transistor cross-coupling ensures that each supplies the other with base current, so the turn-on process is regenerative. Conduction ceases when the C2 is discharged, which happens in about 50µs with the values shown.
Based on the simulation I did, the circuit is not particularly stable and it's usefulness is somewhat doubtful. It's shown only as an example of early attempts. In its day, transistors were still fairly primitive, and there weren't any of the more advanced devices that came along later. In reality, it might not be genuinely useful for anything - there are plenty of patents for things that are either useless, pointless or both.
When wiring an amplifier, it can be surprisingly easy to create an 'accidental' negative impedance converter. All that's required is to fail to ensure that the ground wiring for the audio inputs is connected to the right place. Most amp PCBs will bring the signal wire and its shield (or separate ground wire if the inputs are unshielded) directly to the PCB. If you connect the input RCA (or any other) connector directly to the chassis, it's possible to introduce a positive feedback component into the overall circuit. Consider the drawing below - a small resistance created by the grounding wiring (and/ or the chassis itself) creates a small amount of negative impedance.
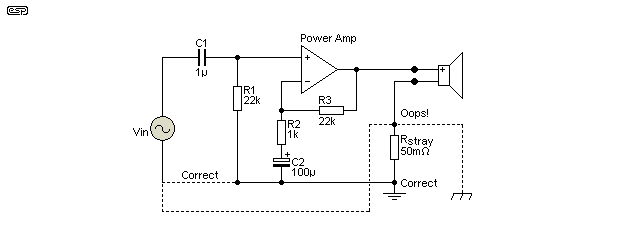
Figure 12 - 'Accidental' Negative Impedance Circuit
The connections shown as 'Oops!' may not seem likely, but it's easier than you might think. If the speaker return is connected to the chassis (and not directly to the filter capacitor centre-tap), simply using grounded input connectors can create this very problem. You need to be very careful with the inputs, and bear in mind that some external equipment (a preamp or radio tuner perhaps) may join the input connectors to the mains earth (ground) lead.
With the values shown for R2 and R3, the amp's gain should be 23 (27dB). These are the values used in most ESP designs, and many others as well. If the wiring from input connectors to the amplifier fails to include a ground (usually via the shield) directly to the amp PCB, the 'stray' resistance (shown as 50mΩ) provides a small amount of positive feedback, increasing the gain to just under 27 (28dB) with an 8Ω load. The gain is load impedance dependent, so it will vary along with the impedance of the loudspeaker. In the example shown, the output impedance is -1.1Ω, which may be enough to cause sound quality to suffer.
As discussed in Project 56 - Variable Amplifier Impedance, very few loudspeaker drivers perform well with negative impedance. This is something I've played with many times over the years, and for the most part it never fails to disappoint. Adding negative output impedance 'accidentally' can be surprisingly easy to do, as it may only be a matter of a ground wire connected to the wrong place. We tend to think that 'ground' is something solid and substantial, but wires have resistance and it doesn't take much to create a problem. In case you're wondering, yes, I have seen this, especially in a 'lash-up' to test the functionality of a new design. If you see the output level from an amplifier increase when a load is applied, you have an 'accidental' NIC.
With an output impedance of -1.1Ω, a +1.1Ω load in place of the speaker will (try to) make the amplifier's gain infinite! I can test this easily with a simulator, but any 'real' amplifier will either oscillate, run out of gain or blow up (all three are possible, and probably in that order). Needless to say I don't recommend this in real life!
<rant> One thing you will find is that the detailed knowledge needed to understand the GIC and other less common (but often quite complex) topologies is often behind 'pay-walls', where you are expected to pay a usually exorbitant amount to get access to the material. In most cases, you are not given anywhere near enough information to know whether the material is relevant or not until you pay for access. IMO this is an abuse of the Net and what it should be for - providing knowledge that you'd find difficult to locate elsewhere. In many cases, organisations are asking full fee payment for material that's over 20 years old, and should be released at no charge. Some readers will know the main offenders, and they are, otherwise, supposedly 'reputable' organisations. Grrrr! </rant>
Now that my rant is over  , we can hopefully get something useful from the details above. Negative impedance is not intuitive, and some of the circuits used are difficult to understand. In some cases, the only way that you can verify that the technique works is to build or simulate the circuit, and simulation has been done for all the examples shown. They all appear to work exactly as described, but reality may be different.
, we can hopefully get something useful from the details above. Negative impedance is not intuitive, and some of the circuits used are difficult to understand. In some cases, the only way that you can verify that the technique works is to build or simulate the circuit, and simulation has been done for all the examples shown. They all appear to work exactly as described, but reality may be different.
You always need to be careful of NICs, because whenever they give very high AC gain, this is often accompanied by very high DC gain. An otherwise harmless DC offset of a few millivolts can become several volts if you don't take care to ensure unity gain at DC. This isn't always possible. By its very nature, a negative impedance is intrinsically unstable. Although many claims may be seen for various NIC circuits, not all stand up to scrutiny (i.e. they may appear to work, but only with an ideal opamp). Others quite clearly cannot work at all, despite mathematical 'proof' that they do what's claimed.
Whether anyone needs the techniques described here is another matter. Mostly, the answer will be "no", but if nothing else it can be very educational to experiment. NICs in general are a fairly uncommon class of circuit, party because there is usually no need for negative impedances, and partly because more traditional techniques are usually more than acceptable to get the results you need.
Using a NIC to drive an audio transformer is one application where there are obvious advantages over the simple opamp drive circuit that is commonly used. Whether it's actually needed is another matter entirely, and it's less complex (and ultimately more 'user friendly') to use a better transformer and be done with it. Negative impedance may be an alternative where cost must be minimised, but careful testing is essential.
Much the same applies to the NIC based bandpass filter. This can provide very high Q at normal audio frequencies with pedestrian opamps. Like all high Q filters it is sensitive to component variations, but it is far simpler than many of the alternative options. These often need esoteric opamps to obtain acceptable results, and are still just as sensitive to component values for the same Q. If you ever need a high (or very high) Q filter, these are definitely worth a closer look.
 Main Index Main Index
 Articles Index Articles Index
|