
 |
| Elliott Sound Products | Frequency Vs. Gain |
 Main Index Main Index  Articles Index Articles Index |
Opamp (aka op-amp or operational amplifier) specifications can be rather daunting, especially if you need gain at high frequencies. This isn't a requirement for audio, but there are many who believe that audio circuitry should be fast. It can be hard to argue with this, because any circuit that's much faster than the signal it's meant to amplify has less opportunity to 'damage' the signal. Very few people would be happy with an analogue preamp circuit that was incapable of providing its full output voltage at 20kHz, even though it will never be expected to do so in any real circuit.
Things are less clear-cut than they appear, particularly with most opamps. There are two parameters that determine the high frequency performance - unity gain bandwidth and slew-rate. If you look at one but ignore the other, things may go badly for your design. The vast majority of modern opamps are internally compensated, which means that they have a natural rolloff at 6dB/ octave from a predetermined (during the opamp's design) low frequency 'corner'. This is often at only 10Hz, so the full claimed open-loop gain (i.e. the gain before feedback is applied) is only applicable for DC or very low frequencies.
Some opamps are internally compensated for a gain of perhaps three or more, and these will oscillate if you attempt to use them for a unity gain buffer (for example). Compensation pins are then made available, so you can add the required external capacitance to ensure stability. The NE5534 is probably the best-known example, and a 22pF compensation cap is recommended for stability with unity gain amplifiers (inverting or non-inverting buffers for example).
Some early opamps had no internal compensation, partly because fabricating capacitors on a silicon die is difficult. The LM301 is one example, and it was recommended that a 30pF capacitor be used for compensation. The datasheet is far from complete, and the performance data are far from complete (compared to modern opamps). Slew rate isn't even mentioned in the specifications section, but from the graphs shown it's rather poor, even with a much reduced compensation capacitor. However, this is a very old design, and it's not a device I'd suggest. You'll still see it used every so often, but it's not advised.
One of the things that anyone working with opamps needs to know is how to follow the info in the datasheet. It would be nice if everyone used the same nomenclature and presented data in the same way, but this is not the case. As a result, you need to be able to interpret the data so you can make direct comparisons. This doesn't always work, because some datasheets leave out things that they consider 'un-necessary'. I doubt that anyone knows just how they decide what is 'necessary' and what's not.
There are two different types of operational amplifier - voltage feedback (VFB) and current feedback (CFB). Most of this article concentrates on 'traditional' voltage feedback types, but current feedback is also covered. They may share the same schematic symbol, but they're very different in the way they are used and how they perform. CFB amplifiers are optimised for very high speed, and cannot be considered to be 'general purpose' devices.
There are two ways that opamps are used when gain is required. The non-inverting configuration is also often used with RF set to zero, and RGain omitted. This is a non-inverting buffer, with unity gain (0dB). If RF and RG are equal, a non-inverting amplifier has a gain of two (6dB) or a non-inverting stage has unity gain (0dB), but with the signal inverted. It's not immediately obvious, but a unity gain inverting amplifier actually has a gain of two - the input is always assumed to be a low impedance, and it must be (very) small compared to RGto achieve unity gain. From the opamp's perspective, this is no different from the non-inverting configuration but with the non-inverting input grounded. It must 'see' a gain of two.
The gain of two (for a unity gain stage) is often known as the 'noise gain', because the circuit has unity gain for the signal (but inverted), but opamp input noise is amplified by two. Note that an inverting stage doesn't require a resistor to ground, as the reference is set by the non-inverting input being grounded. A non-inverting stage must have a ground reference, and that sets the input impedance. The input impedance of an inverting stage is the same as RGain at all frequencies where the opamp operates in the linear region. In some cases it's necessary to add a resistor from the non-inverting input to ground to minimise DC offset. If used, it should be bypassed with a capacitor to minimise noise.

An inverting unity gain stage is therefore twice as noisy as the non-inverting stage. At all gains, the inverting stage operates with 'signal gain + 1' (a gain of 3 means a noise gain of 4). The gain for each stage is easily worked out ...
Non-Inverting, Gain = RF / RG +1
Inverting, Gain = RF / RG
These simple formulae apply for all opamps, including discrete and current feedback types (the latter are a 'special case' discussed below). Knowing the formulae and the reasons they work is essential to your understanding. I've lost count of the number of people who send me an email to ask how to change the gain of a circuit or opamp stage, but this is something that everyone should know. In reality, the relationship is a little more complex, but there is no need to know any of the more 'advanced' maths - the simple versions shown work well enough until the opamp starts to run out of 'excess' gain at high frequencies, and the feedback ratio (set by the two resistors) cannot be maintained any more. That's what this article covers, but the complete formulae are still not necessary.
The value of the bias resistor (RBias) influences the DC offset at the output of the opamp stage. If an opamp draws a 100nA input current, you'll see 100mV developed across a 1Meg resistor. If a capacitor (CG) isn't included in series with RG, any input DC offset voltage is amplified by the stage gain. For a complete guide to designing opamp circuits, see the Designing With Opamps article. In general, allowing opamp stages to have gain at DC is a bad idea for audio, but may be essential for some test equipment and industrial applications.
The bandwidth of an opamp is almost always referred to as the 'unity gain bandwidth' or 'gain-bandwidth product' (GBP). This is the frequency where the gain has fallen to unity (1, or 0dB) without feedback. For mere mortals this is very difficult to measure, but it's easily simulated. A graph showing gain vs. frequency is usually provided in the datasheet, but sometimes it's only stated in the general specifications. When gain (small or large signal voltage gain) is specified, it's almost always for DC or some (very) low frequency.
At least in theory, the gain-bandwidth product tells you the gain you can achieve at a given bandwidth. For example, if an opamp has a gain-bandwidth product (or open loop unity gain frequency) of 1MHz, then if you want a gain of 10 (20dB), the maximum bandwidth (-3dB) will be 1MHz divided by the gain (10). This gives 100kHz. However, there are other factors that must also be considered, and if you only rely on the GBP without considering the peak amplitude and wave shape (we assume a sinewave) things can be very different from what you expected.
An example is shown below, and this was simulated using an RC/MC4558 opamp. These are very common in guitar pedals and they are a cheap option that have better performance than most people expect. They are not in the same league as an LM4562 (for example), but the simulator claims that it has an open-loop gain of 110dB (316,000) and the datasheet says 106dB (200,000). This is shown below, and the simulation is in reasonable agreement with the datasheet. The unity gain bandwidth (also known as gain-bandwidth product) is 3MHz. When used in an audio circuit, there is 44dB of gain available at 20kHz, so if the gain is set for 20dB (×10) there's only 24dB of feedback. Where you might measure a distortion of 0.003% at 1kHz (7V RMS output), that climbs to 0.26% at 20kHz. All opamps are affected in the same way. Note that these results are simulated, not measured. However, measurements will show the same trend with any opamp you care to test.
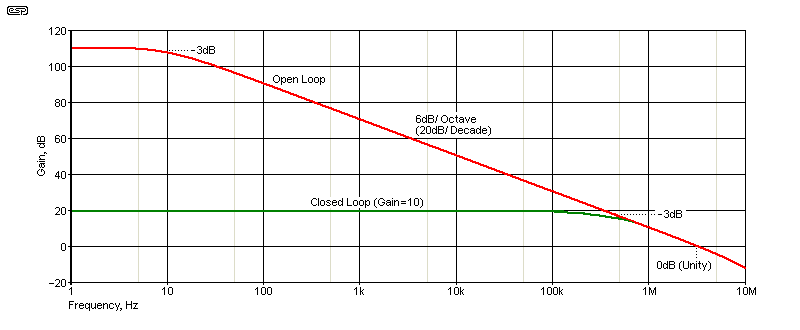
The closed loop shows a gain of 10, or 20dB. The response remains flat until it approaches the open loop gain. Once there's less than 10dB of feedback (when the open loop gain falls below 30dB), the closed loop response falls. For it to be effective, you ideally need at least 20dB of feedback. With decreasing frequency, the FB ratio increases, and at 10Hz there's 86dB of feedback. You might wish that it were different, but physics isn't amenable to the whims of us mere mortals.
Critics of opamps will point to this as a major failing, but in reality it's usually not a problem. It's uncommon for any audio circuit to require a gain of more than 10 (20dB), and if it does it will often be split across two gain stages. However, you need to understand that this is real, so expecting high gain at high frequencies is usually unrealistic. If that's what you need, consider using two opamps in cascade. A total gain of 100 is easy using two gain stages, and at frequencies up to 100kHz with low cost opamps. There will also be circuits where the distortion contribution of the opamp is minimal compared to the distortion expected from the source.
Project 158 shows a low noise preamp with a gain of up to 1,000 (60dB) using NE5532 opamps. By using three stages, each with a gain of 10, you get plenty of bandwidth and very high gain. Ultimately, it was necessary to limit the high frequency response to reduce audible noise. With a gain of 10, an NE5532 can get to 350kHz with a 1V RMS output easily, and there's no visible distortion on a scope until you approach 450kHz.
Circuit design is invariably a series of trade-offs, and a solution for one application doesn't mean that it's suited to another. There will always be situations where good gain 'flatness' is needed, but distortion isn't a major issue, and test equipment is often a case where the requirements are very different from audio applications. Most test equipment that requires a lot of gain is not troubled by a bit of distortion, but gain linearity with frequency is very important. 1dB of variation in an audio circuit will often be quite acceptable, but if a measurement system under (or over) estimates the level by 1dB that may be a 'failure to meet specifications'.
The response shown in Fig. 1.2 is typical of many opamps. The rolloff is 6dB/ octave (20dB/ decade), and it's there because without it the opamp will oscillate. Although shown with a 10Hz -3dB frequency, this varies from one opamp type to the next. Some will start to roll off at a lower frequency, and some higher. The compensation capacitor is known as the 'dominant pole', and it ensures that the opamp will be stable in user's circuits. In the early days there were quite a few uncompensated opamps, such as the LM301, but even that has a required dominant pole capacitor, which is external. The minimum suggested value is 3pF. In some cases, the 'single-pole' compensation is replaced with a two-pole network. This rolls off faster, but the rolloff starts at a higher frequency. Response decreases by 12dB/ octave instead of 6dB/ octave. Not many opamps have this capability, and it's not covered here.
It's not quite so obvious, but for a given -3dB frequency, the bandwidth is also dependent on the open loop gain. If two different devices have a 10Hz -3dB frequency, the one with higher gain must extend the unity gain bandwidth by a proportionate amount. Let's say we have one opamp ('A') with an open loop gain of 10,000 (80dB) and another ('B') with a gain of 100,000 (100dB). Both start to roll off at 10Hz (-3dB). opamp 'A' will have unity gain at 100kHz, but opamp 'B' will still have a gain of 20dB at 100kHz, and will fall to 0dB (unity) at 1MHz. Opamp 'C' doesn't start to roll off until 100Hz, thus extending its unity gain bandwidth to 10MHz, but without increasing the open loop bandwidth.

This is quite clear from the graphs shown above. This relationship holds for all opamps for a given -3dB frequency in the open loop gain. If the -3dB frequency is raised from 10Hz to 100Hz, this has the same effect - the open loop gain is extended by another decade. If the red trace is extended to 100Hz, it would intersect the green trace at that frequency, so it will have a unity gain frequency of 1MHz. The blue trace shows the result if the -3dB frequency is extended to 100Hz with 100dB open loop gain. The use of very high open loop gain to improve bandwidth is seen in the data shown in Table 1.3 (the last three opamps in particular).
It's worth noting that the NE5532/4 are unusual, in that the open loop -3dB frequency is extended to around 1kHz, but open loop gain is lower than most others. By extending the -3dB frequency from 10Hz to 1kHz (two decades), the effective bandwidth is also extended by two decades. Conversely, some opamps start to roll of at less than 10Hz, so while they may seem to have more than enough gain, a lower rolloff frequency limits their closed loop maximum gain vs. frequency. These three parameters are interactive - open loop gain, open loop bandwidth and compensation -3dB frequency. They all need to be considered for a final design where extended high frequency response is required. For most audio applications you don't need to be too fussy, as any opamp with a gain-bandwidth product of 3MHz or more will work fine in most cases.
Note: Not all NE5532/4 opamps are created equal, as they are made by a number of manufacturers. The response referred to above may or may not apply to those you buy. However, the general specifications are usually fairly consistent, so changing brands won't usually cause any problems. This may also apply to other opamps that are available from more than one manufacturer.
The compensation capacitor is selected to ensure that the gain has fallen to unity before the phase shift through the opamp has accumulated 180°. If there is more than 180° phase shift, the signal polarity is inverted, and negative feedback becomes positive feedback, causing oscillation. If you see a specification for 'phase margin', that's the difference between 180° and the actual phase shift through the opamp. For example, a phase margin of 45° means that the opamp has a total phase shift of 135° at its unity gain frequency. You don't need to worry about this for any opamp that's compensated for unity gain. Sometimes it's not specified at all, and in other cases it may be included the the graphs for the device.
Where high speed is essential, there are some truly awesome opamps available if you're happy to pay the price for them. One that's very hard to beat is the AD797 (Analog Devices), which has full output bandwidth to 280kHz. The gain-bandwidth product is up to 450MHz, and you can have a -3dB frequency of 8MHz with 20dB of gain. This doesn't come cheaply though, as they cost around AU$25 - AU$40 each (depending on variant and supplier).
The thing to take away from this is that nearly all opamps require compensation, including discrete versions. You can build an opamp that doesn't require compensation (for example the opamp shown in Project 231, but it still needs to be compensated if you use it with a gain of less than 30dB (×30). Don't expect it to match most integrated opamps that you can buy, but distortion is lower than you'd expect from a simple circuit, and it has a high slew rate (about 6V/µs compensated). You can get response to 1MHz with 40dB of gain (×100), which is a good result. No compensation is needed if you operate it with 40dB of gain, but it's essential for a gain of 30dB or less. See the project article for full details. Current feedback opamps generally don't require compensation in the traditional sense (see Section 4 below).
The NE5534 is well known, and the datasheets should be in everyone's collection. However, the schematic is not easy to follow, so I've used the RC4558 as an example of a 'real' circuit diagram. This is fairly straightforward, and it gives you an idea of the complexity of even a simple, comparatively low-performance opamp.
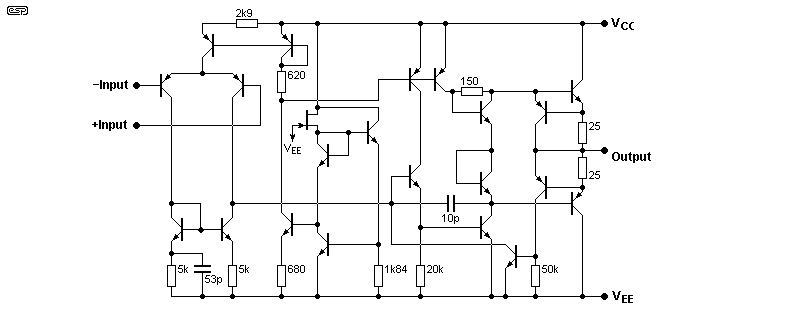
The 'dominant pole' is the 10pF cap. This is sufficient to allow the circuit to remain stable with unity gain. Some datasheets don't mention the minimum gain without compensation, but it's usually about ×3 (or 10dB). The TI datasheet is well filled with graphs of the essential parameters. The common way to ensure stability is to use a 30pF compensation cap (33pF is the closest standard value). With this connected between pins 5 and 8 of an NE5534, the slew rate is reduced to 6V/µs (it's 13V/µs without compensation). Interestingly, the lowly TL07x JFET input opamps also have a slew rate of 13V/µs, and they are internally compensated for unity gain, but with a gain-bandwidth product of only 3MHz.
The values from the 'Typical' column of the NE5534 datasheet show that it has a large signal gain of 100V/ mV (100,000 or 100dB). The slew-rate is claimed to be 13V/ µs, but (and this is important) that figure only applies when there is no external compensation capacitor. If a 22pF compensation cap is included, the slew rate falls to 6V/ µs - a significant difference.
If your input signal is a sinewave and the output becomes triangular at high frequencies, it's slew rate limiting. The opamp isn't fast enough to keep up with the signal, and the opamp is operating open-loop (no feedback) during this period. The old claims of TIM/TID (transient intermodulation distortion/ transient induced distortion) were based on exactly this phenomenon, but failed to understand (or chose to ignore) the fact that no audio signal in a properly designed circuit will ever be fast enough to cause a problem. In all but a few cases, TIM was a furphy - it simply didn't happen. It was (and is) easy to create it, but not with a normal audio signal (e.g. music).
The slew rate needed in any application depends on the frequency, waveform and amplitude. A 20kHz sinewave signal at 2V RMS (2.82V peak, typical of the maximum output from a preamp) has a maximum rate of change (slew rate) of 365mV/µs, but if the amplitude is increased to 10V peak (7V RMS) that increases to 1.26V/µs. Increase the frequency to 30kHz (still at 10V peak) and the slew rate becomes 1.88V/µs. If we were designing a measurement system that has to extend to 100kHz, the slew rate increases to 6.28V/µs.
This applies irrespective of the opamp's unity gain bandwidth. An NE5534 without external compensation has a slew rate of 13V/µs, reduced to 6V/µs with a 22pF compensation capacitor. It's apparent that to be able to get 10V peak output at 100kHz, an NE5534 must be used without the compensation cap, or its output cannot change fast enough to keep up with the signal. Slew rate for a sinewave is determined by the formula ...
Slew Rate = 2π × f × VPeak V/s
We divide that by 106 (1,000,000) to obtain V/µs
It's of no consequence that the open loop bandwidth is 10MHz with the 22pF cap in circuit. The maximum frequency and/or amplitude is limited by the slew rate if we expect more than a couple of hundred millivolts at frequencies up to 1MHz. Slew rate has other effects on a circuit too. If an opamp is driving a nonlinear load (such as an analogue meter's rectifier), the output may have to swing by 1V or more just to overcome the diodes' forward voltage. Ideally, this will be close to instantaneous, but no circuit, opamp or discrete, has an infinite slew rate, so operation at high frequencies is compromised.
Test instrument circuits are a 'special' case, and it can come as a real surprise when an opamp that looks like it should easily handle the highest frequency of interest falls apart during testing. The response may fall dramatically well before you thought it should, so your meter circuit that should handle 250kHz only makes it to 50kHz before the response is well down from where it should be. Even a simulated circuit using an 'ideal' opamp (almost infinite bandwidth and slew rate) may prove disappointing, and it can be hard to understand why.
The frequency response you can get from any opamp is limited by its unity gain bandwidth and the slew rate. At unity gain, the response will usually extend to the unity gain bandwidth, but you can only get an output voltage that remains below the slew rate. At low levels, you can usually expect to get up to the full bandwidth claimed for a non-inverting amplifier (buffer), but somewhat less for an inverting amplifier. This is because an inverting buffer has a 'noise gain' of two, and the opamp is behaving exactly as it would if it had a gain of two. The -3dB frequency will be a little less than half that for a non-inverting buffer.
You have to look at the open-loop gain plot to see why this is true. Unfortunately, the graph resolution is never good enough to see this clearly, but it's always the case. This may be unexpected if you're not fully acquainted with all the specifications and their implications. As an example, a simulation using a TL072 opamp shows the -3dB response extending to 4.86MHz for a non-inverting buffer, reduced to 2.25MHz for an inverting buffer. The same effect applies to all opamps!
The next issue is the maximum output voltage at the highest frequency of interest (let's say 1MHz). We know that the TL07x series have a slew rate of 13V/µs, so any voltage (at any frequency) that exceeds that means that the level will be severely limited. Using the formula shown above, it's easy enough to see that 2V (peak) is the absolute maximum for a 1MHz signal, but in reality it will be a bit less to retain linear operation. Remember that when any feedback circuit has entered slew rate limiting, it's no longer linear and it has zero feedback. A simulation shows that a TL072 has an absolute maximum of 1V RMS (1.414V peak) before slew rate limiting causes a loss of feedback. With 1MHz at 1V RMS, the outputs of both inverting and non-inverting amps are reduced - you can't get unity gain when you're so close to the limits.
It's not only frequency response that's affected when you push an opamp to its limits. With a circuit gain of x10 (3.16dB) you need at least 20dB of excess gain, and preferably more, at the highest frequency of interest. Referring to Fig. 1.2, if you require a gain of 10, the output will be flat to within 1dB up to 60kHz. At that frequency, the open loop gain has fallen to 35dB, so there's only 15dB of feedback. There's 20dB of feedback available at about 33kHz. At the highest (audio) frequency needed (20kHz) you have a total of 46dB of gain, allowing 26dB of feedback. As the amount of feedback is reduced, distortion increases in (almost) direct proportion.
| Opamp | Open Loop Gain | Slew Rate | Unity Gain B/W |
| 1458 | 200 V/mV (106 dB) | 0.5 V/µs | 1 MHz |
| 4558 | 200 V/mV (106 dB) | 1.6 V/µs | 2.8 MHz |
| TL07x | 200 V/mV (106 dB) | 13 V/µs | 3 MHz |
| LM833 | 316 V/mV (110 dB) | 7 V/µs | 15 MHz |
| NE5532 | 100 V/mV (100dB) | 9 V/µs | 10 MHz |
| NE5534 (CC=0) | 100 V/mV (100 dB) | 13 V/µs | 10 MHz |
| NE5534 (CC=30pF) | 100 V/mV (100 dB) | 6 V/µs | 10 MHz |
| OPAx134 | 1 V/µV (120 dB) | 20 V/µs | 8 MHz |
| OPA1642 | 5 V/µV (134 dB) | 20 V/µs | 11 MHz |
| AD744 | 400 V/mV (122 dB) | 75 V/µs | 13 MHz |
| LM4562 | 10 V/µV (140 dB) | 20 V/µs | 55MHz |
| AD797 | 20 V/µV (146 dB) | 20 V/µs | 110 MHz |
CC is the compensation cap for the NE5534. It's interesting to compare the parameters that ultimately limit the high frequency performance. As you can see from the table, the NE553x devices have less open loop gain than 'lesser' devices, but have a much wider bandwidth. The TL07x opamps have a very high slew rate, but can't get beyond 3MHz. The OPA134 (or dual OPA2134) has a very high slew rate, but it can't beat an NE5532 for maximum frequency. The LM4562 has the same slew rate as the OPA134, but it has a gain-bandwidth product of 55MHz vs. only 8MHz. The AD744 has a slew-rate of 75V/µs (faster than any of the others listed), but according to the datasheet only manages 13MHz unity gain bandwidth.
It should come as no surprise that this confuses people. It is confusing, and these examples show why you can't just look at one parameter when high speed and/ or wide bandwidth is required. The parameter that affects your circuit (for better or worse) depends on the application, the highest frequency of interest, and the expected signal amplitude at that frequency. If you simply select the fastest opamp you can get (based on the gain-bandwidth product), it may be unable to supply the full output level at the highest frequency because the slew rate is too low. Likewise, if you select on slew rate, the bandwidth may be inadequate (the TL07x is a good example - 13V/µs. but only 3MHz bandwidth).
Another specification that is supplied for some devices but not others is full-power bandwidth. This is the -3dB frequency at maximum output swing before clipping or slew-rate limiting. I didn't include it in the table because it's not always specified. Sometimes it's provided in the device parameters, sometimes it's shown as a graph, and sometimes it's not included at all. Where this is made available, it's almost always for a unity gain, non-inverting stage.
The simple CFB amplifier (aka CFA) shown below is configured for a gain of 3 (9.54dB), has flat response to 26MHz, and a slew rate of around 280V/µs. The two input transistors are not within the feedback loop so their distortion is dominant. Just like its integrated brethren, the high frequency response is controlled by the value of RF. This simple version can't compete with an integrated circuit, but it shows how the feedback is applied. Instead of going to the base of a transistor, it's applied to the emitter(s). This is a low-impedance point in the circuit that responds to current - hence the term 'current feedback'.
The CFA was patented in 1985, but was 'discovered' in around 1982 [ 6 ]. Many early transistor power amplifiers used the current feedback topology, well before anyone had named it as such. The Mullard 10-10 stereo amplifier is an example, published in the 1960s. A number of similar designs were popular around that time and into the 1970s, and almost all used the current feedback topology. Voltage feedback became common when most designers switched to using a long-tailed pair for the input stage.
CFAs are also known as 'transimpedance' amplifiers. To make everyone's life miserable, it's customary to state the gain in ohms. Essentially, it's a measurement of how many volts output you get for a given input current, and volts divided by amps is ohms. A particular CFA may have a 'gain' of 600kΩ, which means that for each milliamp of input you get 600V output. This is clearly impossible, but it's easily scaled. In this case, an input current of 1µA would cause a 600mV output voltage (600mV / 1µA = 600k). Fortunately, you don't need to get your head around this and it's unlikely that too many readers will be rushing out to buy current feedback opamps. You also need to be aware that the term 'transimpedance amplifier' may also refer to a voltage feedback opamp configured as a current to voltage converter. It's rather disappointing that the two seem to have been conflated, for reasons that escape me.
DC offset is usually somewhat higher with CFB opamps than VFB types, and the simulated version of the Fig. 4.1 circuit has an offset of over 40mV with the +ve input grounded via a 1k resistor. This is despite simulator transistors being well matched. It's an issue with all such designs, whether discrete or integrated. Capacitive coupling eliminates the DC offset of course, but that may not be possible in some circuits. The simulated version has a distortion of 0.33% with 3V output and no output load other than the feedback network. The circuit can drive 10MHz into a 50Ω load at up to 4V peak (5.6V RMS). Due to its simplified topology, distortion performance is rather poor if it's heavily loaded. As shown (using BC549/559 transistors), the -3dB bandwidth is 38MHz (simulated).
There used to be only a few opamps using current feedback, rather than the more common voltage feedback. Over the years, the number has grown dramatically, and there are now countless examples. These can usually be recognised by the use of a very low value feedback resistor, and they are designed to operate in the MHz ranges. They will work just fine for audio, although some have a low input impedance. An example is shown in the article High Speed Amplifiers in Audio, published after Texas Instruments sent me some to play with. These have a -3dB bandwidth of up to 200MHz, and were designed to drive xDSL (digital subscriber line) - a twisted pair telephone line used for data. This technique has lost favour in most countries now (supplanted by cable/ fibre optic connections), but for quite a while it was the preferred method of providing high speed internet connections to customers. It's still used, and CFB opamps are likely to be with us for quite some time yet, because designers have found them to be useful for many other tasks.
The ability to transmit multiple carrier signals onto a single twisted pair was revolutionary at the time, but it required amplifiers with very wide bandwidth and extremely low distortion. Current feedback opamps are now very common, and they are ideal for handling very high frequencies. Unlike a voltage feedback opamp, CFB opamps do not use a dominant pole for compensation, so they have fairly flat response from DC to daylight (well, not quite daylight, but you get the idea).
CFB opamps are well suited to video line drivers, intermediate frequency amplifiers (in radio receivers) and anywhere that very good high frequency response is needed. There are no audio systems that need this much speed, but it probably won't hurt anything. You do need to be aware of DC offset, and in extreme cases you might find that using a CFB opamp in an audio system causes it to pick up radio frequency interference. This is unlikely to be what you want to achieve. Note that you cannot (and must not) add a capacitor in parallel with RF to limit the HF response, as that will cause oscillation. Instead, use a higher value feedback resistor, or a simple passive filter at the non-inverting input.
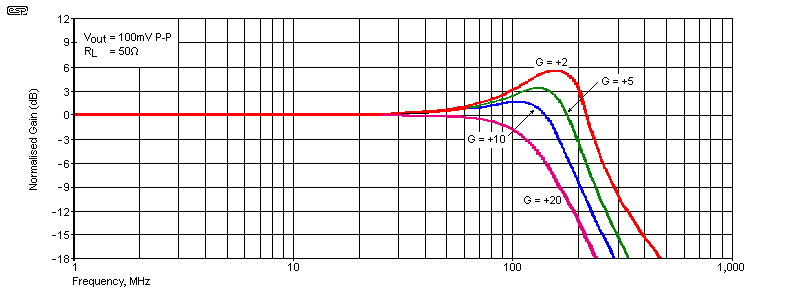
An example of a current feedback amplifier (CFA) is the Analog Devices ADA4310. The response curves are shown above for four gain settings. This particular device has various power settings, and the graphs shown are with it set for maximum power. As power is reduced, so is bandwidth. Don't expect to find these in any audio products. Doing so would be rather pointless, although their input impedance is within the normal range we expect. The ADA4310 datasheet claims 500k input impedance. If the feedback resistor is made lower than the recommended minimum a CFA will show greater peaking and may become unstable. Feedback resistors higher than the suggested range should also be avoided. The maximum supply voltage for the ADA4310 is ±6V, limiting dynamic range for audio applications.
Note: Selecting the feedback resistor using the same criteria you'd adopt for a voltage feedback opamp could easily see the bandwidth reduced by an order of magnitude (e.g. from 100MHz down to only 10MHz). The values suggested in the datasheet are there for a reason! Also, be aware that the open-loop gain is generally lower than most VFB opamps, so expecting very high closed loop gain is usually unrealistic.
| Gain (dB) | RF (Ω) | RG (Ω) | -3dB Bandwidth |
| +2 (6dB) | 499 | 499 | 230 MHz |
| +5 (14dB) | 499 | 124 | 190 MHz |
| +5 (14dB) | 1k | 249 | 125 MHz |
| +10 (20dB) | 499 | 55.4 | 160 MHz |
| +20 (26dB) | 499 | 26.1 | 115 MHz |
The symbol for a CFA is usually the same as used for voltage feedback devices, but the feedback resistances used are far lower. The maximum suggested value for the feedback resistor for the ADA4310 is 499Ω (510Ω would work too), and these devices are designed to drive 50Ω loads. It's common to see the gain rise before it starts to roll off, and the rise is greatest when a CFA is set for low gain. CFAs generally have low distortion and extraordinarily high slew rates. The CFA shown has a maximum slew rate of 820V/µs. Input noise is claimed to be only 2.85nV/√Hz.
Power dissipation in CFAs is generally higher than a 'normal' voltage feedback opamp, and some require a heatsink. The supply current for the ADA4310 is 15.2mA (full power mode), so dissipation is 182mW - not much, but it's a tiny SMD IC. The first integrated CFA I played with was a TI THS6012, a fairly substantial device that also required a heatsink that was very difficult to accommodate. One interesting claim is that CFB opamps have bandwidth and distortion characteristics that are 'relatively unaffected' by the gain. Most application circuits shown in datasheets indicate a maximum gain of up to ×10 (20dB), but ×4 (12dB) is more common.
The very wide bandwidth of CFAs can mean that cables are no longer 'unimportant'. Because of their very high maximum frequency, a short length of coaxial cable can become a resonant circuit. This can happen with 'ordinary' opamps as well, but at the frequencies where a cable can cause problems they have little or no gain. A 857mm length of coax is 1/4 wavelength at 70MHz, well within the bandwidth of most CFAs. To prevent reflections and potential instability, coax should be terminated with its characteristic impedance. This is a nuisance (to put it mildly). Adding a 51Ω resistor in series with the output will generally work well enough.
Another CFB opamp worth looking at is the OPA2677, with a small-signal bandwidth of 220MHz and a slew rate of 1,450V/µs. The suggested feedback resistor (RF) is 511Ω, or 250Ω for a maximum bandwidth of 150MHz. The maximum supply voltage is +12V (or ±6V). If you think either of these devices suit your needs, you need to read the datasheet carefully and observe all precautions. Supply decoupling is particularly important, and MLCC types are the only ones that will ensure good performance. In general, multiple values in parallel are generally used to cover the frequency range. Normally, I never suggest this for audio, but when you're working with RF, everything changes. The supply current for the OPA2677 is 18mA for both channels, but it can supply up to ±380mA to the load.
Several ESP projects are CFAs. The Project 37 (DoZ) preamp is one example, and the Project 217 'practice' amplifier is another. The P37 preamp has no compensation, and response extends to 10.5MHz (-3dB), with a unity gain bandwidth of 25MHz, and a slew rate of 36V/µs. All of this from just four transistors! While these figures were taken from a simulation, measurement has shown a small signal -3dB frequency of 8MHz which is extraordinary for such a simple circuit. It's quite capable of providing 3V peak output at well over 1MHz, something that is difficult with most opamps.
It's important to understand that there are two different versions of current feedback. The first is the type discussed here, and the second is used to increase the output impedance of amplifier circuits, as described in Project 27 (guitar amplifier) and Care & Feeding Of Spring Reverb Tanks. Both use current feedback, but it's used to sense the current in the load, and is not a characterisation of the amplifier topology. That both use the same terminology is unfortunate, but a quick look at the circuit of one or the other will allow you to figure out what you're looking at. Current feedback used to increase output impedance is almost invariably a mixed feedback system, using both voltage and (load) current feedback paths, with the current sensed across a low value resistor.
There are several references to the loss of feedback in this article, and it's helpful to understand how this happens. Feedback works by sending a scaled version of the output back to the inverting input of an opamp (or power amp). Provided the circuit is operating in linear mode (not distorting for any reason), the voltage at the two inputs (+ve and -ve) will be equal. This assumes an 'ideal' device, and in reality there is always a small difference, but for basic analysis it can be ignored.
Should the device become non-linear for any reason (e.g. clipping or slew rate limiting), it's no longer possible for the input voltages to be equal because the output is not linearly related to the input. Simple deduction tells us that if the device's input voltages are not the same, it can only be operating open-loop - the feedback is no longer in control of the circuit's behaviour. The output is simply controlled by the relative polarity of the two inputs. In this (non-linear) mode of operation, the output simply assumes the polarity of the most positive input.
If the non-inverting input is more positive than the inverting input, the output will be positive, and vice versa. Normal (linear) operation can only resume when the feedback is restored. As noted, this can happen if the input changes too quickly and the output can't keep up (slew rate limiting), or if the output is driven to one or the other supply rail (clipping). This phenomenon was the basis for the arguments that raged (for a while) about TIM (transient intermodulation [distortion]) aka TID (transient induced distortion). It's very real, and it can happen, except that there were presumptions made that failed to account for the nature of music. Musical instruments (and the recording processes) don't have anything that changes fast enough to cause problems with a properly designed circuit.
It's very easy to create TIM/TID on the test bench and in a simulator, but you can use the formula for maximum slew rate to work how fast an amplifier needs to be to handle normal audio. It's almost impossible to cause TIM/TID with music alone. To give you an idea, an amplifier with ±100V supplies will never be driven to more than ±50V with an audio signal of 20kHz, but we'll ignore that and work out the slew rate for 100V peak at 20kHz. That works out to be 12.6V/µs, which is total overkill, but easily achieved.
For more sensible power ratings (not everyone needs a 600W/ 8Ω amplifier), the demands are similarly reduced. A more typical power amp will use ±50V supplies (150W/ 8Ω) and will never have to provide full power at 20kHz - the worst case is around 35W otherwise everyone would blow up their tweeters. The slew rate needed for that is only 2.5V/µs!
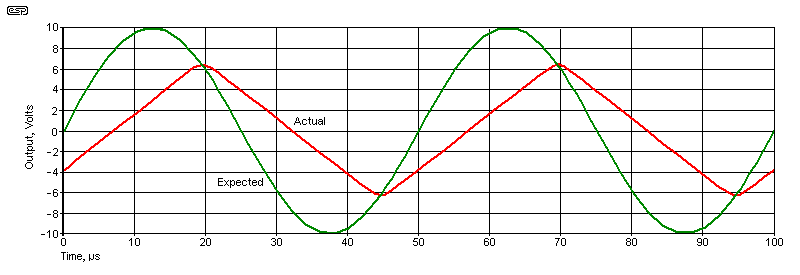
Fig. 5.1 shows what happens when the output (red trace) can't keep up with the input. The input signal was a 1V peak sinewave at 20kHz. The output is unable to change quickly enough to permit the passage of a sinewave, so a triangular wave is produced instead. I used a 741 for the simulation, as it is one of the few that will limit at audio frequencies. Its slew rate is only 0.54V/µs. The required slew rate is 1.26V/µs, as the frequency is 20kHz with an expected peak voltage of 10V. This condition will always exist at some frequency (and/ or level), but with most 'decent' opamps you won't see it until the input frequency is over 50-100kHz. For example, an NE5532 with a 10V peak output will show the onset of slew rate limiting at around 130kHz. At 100kHz there's no limiting, and distortion is under 0.1%. This is of no consequence of course, as it's well above the audio band. CFB opamps are different, and they are generally fast enough that slew rate limiting won't occur.
It's a good idea to ensure that the slew rate is at least double that which is needed for clean reproduction, and that's usually fairly easily achieved. None of this helps if the amp is driven to clipping, and while that's ideally avoided, it will happen occasionally. For power amplifiers, ensuring a clean recovery from clipping can be more important than slew rate. Clean recovery from clipping is particularly important for guitar amps, as they are usually driven hard.
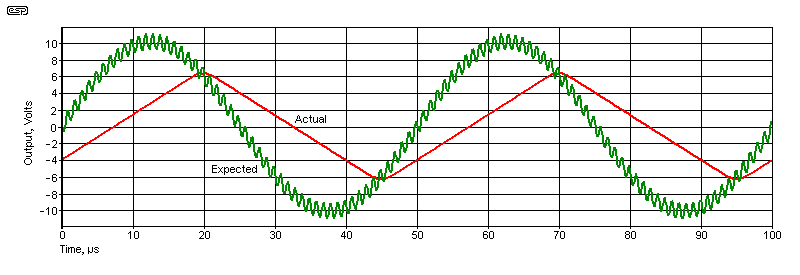
Fig. 5.2 shows SR limiting in more detail. The input signal was a 1V peak sinewave at 20kHz, with a small 1MHz sinewave superimposed. The amplifier is supposed to provide an output of ±10V peak (7V RMS) as shown by the green trace, and it should include at least some of the 1MHz signal. As before, the opamp's output can't keep up. The output tries to get to the required voltage, but it can't reach the ±10V peaks quickly enough. As you can see, all traces of the added 1MHz signal have gone. The opamp is operating open-loop - the feedback is irrelevant.
Fairly obviously, any 'nuances' in the input signal are lost, as is the original waveform. This is intended to be exaggerated so you can see the effects easily. If slew rate limiting occurs in a 'real' circuit it's far more subtle, and it may even go un-noticed. You'll never see it happen on a scope with a music signal because it happens too quickly and the signal is dynamic. It is very easy to induce though, and if you observe the output of a slow opamp stage that's expected to provide (say) 10V peak at 20kHz, you will see the output waveform almost exactly as shown (the frequency may be much higher before the problem is visible). As shown, it will show as a drop of 5.26dB if you only monitor the output with an AC millivoltmeter. If the input level is reduced to 250mV peak (1.77V RMS output) the problem goes away, and the output of even a slow opamp is flat to well over 20kHz, with distortion back to 'normal' (ignoring the 1MHz signal - that's only there to show what happens during slew rate limiting). Fairly obviously, choosing a more sensible opamp also solves the problem - no-one would use a 741 in an audio circuit other than for testing, and even that's unlikely for the most part.
Note that Fig. 5.2 is a test designed to show not just slew rate limiting, but what happens to other frequencies that may also be present. No-one will have an audio signal with 1MHz (or other high frequency) superimposed, but there will be harmonics of other signals present. The example is extreme, and it will never happen with music. If you were to run a bench test with the setup described, you will see the same thing. Examples such as this can be used to 'prove a point', but they do not represent what happens with music. For what it's worth, an LM4562 will show an output that's very close to the 'expected' (green) waveform. If a 1MHz signal were somehow present along with the audio, it should be filtered out as it serves no useful purpose and will probably increase distortion.
With opamps used in low-level circuits (preamps, active crossovers, line drivers, etc.), the demands are generally fairly modest. The 'old faithful' NE5532 (or 5534) opamp has been used in countless high quality mixing consoles used to create the music you listen to. It stands to reason that they are also perfectly suited to home equipment. From the basic (frequency related) specifications provided in Table 3.1, it's obvious that they will never cause problems in most audio circuitry. The LM4562 (and its close relatives) used to be very expensive alternatives, but these opamps are now barely more expensive than the NE5532, so it would almost be silly not to use them. Unfortunately (and in common with so many other parts), through-hole (DIL) packages may be hard to find.
This article will not answer the all-important question of 'which opamp is best'. There is no 'best' opamp for all applications, the range of devices is truly vast, and while some are acclaimed as sounding 'better' or 'worse' than others, mostly this is nonsense. It certainly applies if there's audible noise, or if you try to use a completely inappropriate opamp (e.g. µA741 or 1458) for audio, but with reasonable signal levels (up to 1V RMS) and across the audio band, even these work. They are far from optimum though, and I would never suggest that you remove an LM4562 and use a 4558 instead. The NE5532/4 are still excellent opamps, and their only real issue is a rather high DC offset voltage due to their comparatively high input bias current. This is easily solved by using AC coupling - you can't hear DC, so there's no reason to amplify it.
Note that every IC opamp ever made has full gain at DC (that's where the open-loop gain is measured), and all have almost identical low frequency performance (noise excepted). The differences are in the higher frequencies, where the open-loop gain is falling at 6dB/ octave and feedback becomes less effective. If you need to amplify high frequencies, then you must examine gain-bandwidth product (unity gain bandwidth), slew rate and 'full power' bandwidth if that's provided in the datasheet.
The selection of an opamp for instrumentation is usually far more difficult than for audio. Test equipment needs flat frequency response, often to 250kHz or more, but there may be no need for particularly low distortion. In some cases, DC accuracy may be an absolute requirement, while in others it doesn't matter at all. Many test instrument circuits make greater demands on opamps than any audio circuit, as there are many criteria that must be satisfied. This is why manufacturers have such detailed datasheets, so you can wade through all the parameters to choose the device best suited to your needs.
You often need to be very careful with wide bandwidth opamps, as a minor error in PCB track layout can cause the device to oscillate. Some are more resistant to oscillation than others, and regular readers will have noticed that I never specify the LM833 for any projects. Many people have found these opamps to be marginally stable unless everything is done perfectly. In extreme cases, just adding a socket can cause (often serious) problems, and it's essential that opamps always have a bypass capacitor as close as possible to each supply pin. The bypass can be between the two supplies, but bypassing each supply to ground is also essential. More problems are caused by poor (or non-existent) bypassing than almost any other design error.
Sometimes an oscillation problem is 'invisible'. Nothing shows up on a scope, but distortion may be higher than expected. The problem may 'go away' (or appear) if you touch the IC body, or connect/ disconnect a test lead. This generally indicates that the opamp is oscillating internally, with little or no visible clue. Should you experience this, it's almost invariably due to poor bypassing. There might be other causes, but proper bypassing is so important that you need to be aware of all possible issues if it's not done properly.
This article covers but one aspect of opamp design - speed/ frequency response. Depending on the application, you may also need to optimise for noise (see Noise In Audio Amplifiers) or distortion (Distortion - What It Is And How It's Measured). For high quality audio, both of these are essential, but bandwidth is rarely an issue if an 'audio qualified' opamp is selected. Be aware that even major manufacturers may make (IMO silly) claims for 'audio quality' with nothing to back it up.
Most references are the datasheets for the various devices mentioned throughout the article. There aren't many 'independent' references, because the topic (frequency vs. gain) is not well covered elsewhere, and much that you find is not useful. CFAs are very well documented, but many of the explanations are rather convoluted. There are some references though ...
 Main Index Main Index  Articles Index Articles Index |