

|
| Elliott Sound Products | Passive Crossover Design Tables |
 Main Index
Main Index
 Articles Index
Articles Index
There are several crossover design programs available, some free, and others with variable price ranges. There seems little doubt that these can make your life easier, but for many people the 'old' techniques are still preferred. You also have to consider the learning curve - most of these programs will take some time to master. I make no recommendations for design software, but be aware that many will require data inputs that may not be available in the format needed. Should that be the case (or where detailed data are not available), you will need to characterise the drivers yourself, and it may not be possible to provide the required data in the format needed. Some of this software is a 'normal' executable program, while others use a spreadsheet. Neither is necessarily better or worse than the other, but one must admire the amount of work involved to get usable results, regardless of how the data are manipulated.
Most design programs are complex by necessity, and while they will always give you a result, it can only ever be as good as the data you can provide. The tables and formulae shown here can be made to work with any driver, provided you know how to measure the characteristics and/ or provide impedance compensation to ensure that the drivers appear resistive across the crossover region.
The tables shown below can be used for the calculation of passive filters (first, second, third, and fourth order) in 2-way and 3-way crossover networks. After deciding on the topology you want, you need to know the corrected impedance of the tweeter, woofer and midrange (for a 3-way network). There are quite a few configurations that I've left out, because they are either sub-optimal or a bit too far from 'conventional' alignments. If you want all of the formulae, I suggest that you buy the book shown in Reference #1 (or the latest revision). There are many other texts on the same topic, but I don't have them and cannot comment on their usefulness.
For 2-way systems, the mid-bass/ woofer will almost always require a Zobel network to correct the impedance rise due to Le (voicecoil inductance). The tweeter will likewise almost invariably require a notch filter to suppress the resonant peak, for both 2-way and 3-way systems. While it is certainly possible to design a filter that works without any impedance compensation, it will be much more difficult and time-consuming to do so.
With a 3-way system, the midrange driver may require both a Zobel network and a notch filter, depending on its resonant frequency. The notch may not be necessary if the resonance is more than two octaves below the crossover frequency (for example midrange resonance at 75Hz for 1 300Hz crossover frequency). This is something that must be tested thoroughly before you'll know if it causes any measurable (or audible) problems. All formulae are based on the premise that the driver impedance is resistive, having been equalised as necessary. Do not use the nominal impedance of the drivers, as the results will be highly unpredictable.
The circuits shown do not include impedance EQ. See the companion article Impedance Compensation For Passive Crossovers.
Driver impedance correction must be determined before using these tables, and the measured (equalised) resistance used. This will typically reduce the impedance of each driver by around 20% or more, with the average being roughly equal to the driver's electrical voicecoil resistance (re). Failure to provide impedance EQ will usually result in an unsatisfactory end result, and be aware that the EQ networks will add many more parts (inductors, capacitors and resistors). No provision is made here for determining the relative levels from each driver, and L-Pads are likely to be needed for tweeters and midrange drivers to ensure that their levels match the woofer. Ensure that the woofer has the lowest efficiency (in dB/W/m) or it will be difficult to get the levels correct.
The crossover component values are calculated using the following formulae (adapted from 'The Loudspeaker Design Cookbook' by Vance Dickason). Not all variations are covered, only those that are in common usage, and the 'esoteric' versions have been culled to make the tables more readable. Make sure that you use the correct table, especially for 3-way designs. The values are different, depending on the upper and lower crossover points. Formulae are provided for a range of 10 (e.g. 300Hz to 3kHz, 3.4 octaves) and a range of 8 (e.g. 375Hz to 3kHz, 3 octaves).
Circuit diagrams are shown for 1st, 2nd and 3rd order networks (6dB, 12dB and 18dB/ octave respectively). I've not included schematics for 4th order networks because their complexity and component sensitivity is such that getting a good result will either be extremely difficult/ expensive or (usually) both. Impedance equalisation becomes (even more) critical, and small errors can cause large variations in performance. This doesn't mean it can't be done, but the cost is such that active filters (and multiple amplifiers) will give better, more predictable performance for less financial outlay and a greatly reduced risk of failure.
While you can choose any of the alignments to suit your needs, the ones I recommend are indicated by a star/ asterisk (*). Capacitance is in Farads, inductance in Henries and resistance/ impedance in Ohms.
| 1st Order Butterworth * | ||
|---|---|---|
| C1 | 0.159 / rH f | |
| L1 | rL / 6.28 f |
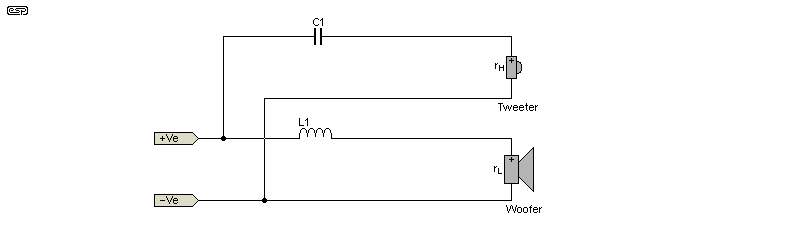
Figure 1 - 2-Way 6dB/ Octave Crossover
While the above shows a parallel network, IMO a series network is preferred for first-order 2-way systems. Although the two are theoretically identical with a resistive load in place of the speaker drivers, a series network doesn't need impedance compensation. See the article 6dB/ Octave Passive Crossovers for more on this (slightly unusual) configuration.
2nd Order 2-Way
| 2nd Order Butterworth | 2nd Order Linkwitz-Riley * | |
|---|---|---|
| C1 | 0.0912 / ( rH f ) | 0.0796 / ( rH f ) |
| C2 | 0.0912 / ( rL f ) | 0.0796 / ( rL f ) |
| L1 | 0.2756 rH / f | 0.3183 rH / f |
| L2 | 0.2756 rL / f | 0.3183 rL / f |

Figure 2 - 2-Way 12dB/ Octave Crossover
3rd Order 2-Way
| 3nd Order Butterworth * | 3nd Order Bessel | |
|---|---|---|
| C1 | 0.1061 / ( rH f ) | 0.0791 / ( rH f ) |
| C2 | 0.3183 / ( rH f ) | 0.3953 / ( rH f ) |
| C3 | 0.2122 / ( rL f ) | 0.1897 / ( rL f ) |
| L1 | 0.1194 rH / f | 0.1317 rH / f |
| L2 | 0.2387 rL / f | 0.3294 rL / f |
| L3 | 0.0796 rL / f | 0.0659 rL / f |
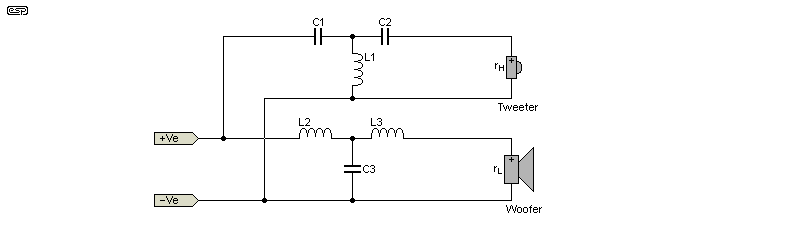
Figure 3 - 2-Way 18dB/ Octave Crossover
4th Order 2-Way
| 4th Order Butterworth | 4th Order Linkwitz-Riley * | |
|---|---|---|
| C1 | 0.1040 / ( rH f ) | 0.0844 / ( rHf) |
| C2 | 0.1470 / ( rH f ) | 0.1688 / ( rHf) |
| C3 | 0.2509 / ( rL f ) | 0.2533 / ( rLf) |
| C4 | 0.0609 / ( rL f ) | 0.0563 / ( rLf) |
| L1 | 0.1009 rH / f | 0.1000 rH / f |
| L2 | 0.4159 rH / f | 0.4501 rH / f |
| L3 | 0.2437 rL / f | 0.3000 rL / f |
| L4 | 0.1723 rL / f | 0.1500 rL / f |
The 4th order network circuit is not shown, as its complexity is such that 4th order networks are best achieved using active filters. High order passive filters are not recommended. The cost and complexity rapidly become such that the cost will be far higher than an active solution. This is especially true when you consider the component sensitivity - the parts used need to be selected for close tolerance or the filter response will not be accurate.
For all 3-way designs, the midrange 'centre' frequency is determined by fM = √( fH × fL ) or ( fH × fL )^0.5
Select either fH / fL as 10 (3.4 octaves) or 8 (3 octaves)
| 1st Order Normal Polarity * fH/fL = 10 | 1st Order Normal Polarity *
fH/fL = 8 | |
|---|---|---|
| C1 | 0.1590 / ( rH fH ) | 0.1590 / ( rH fH ) |
| C2 | 0.5540 / ( rM fM ) | 0.5070 / ( rM fM ) |
| L1 | 0.0458 rM / fM | 0.0500 rM / fM |
| L2 | 0.1592 rL / fL | 0.1592 rL / fL |
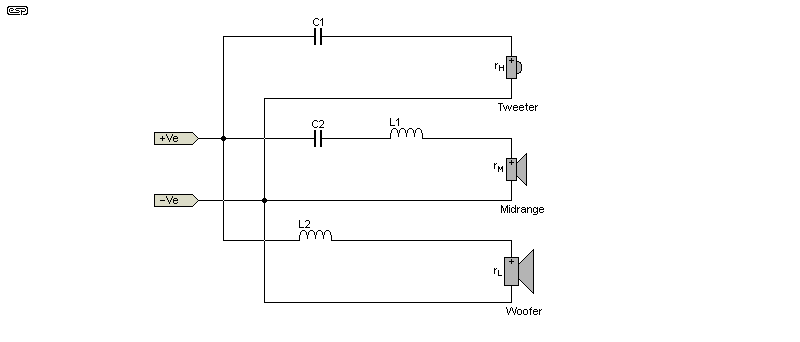
Figure 4 - 3-Way 6dB/ Octave Crossover
2nd Order 3-Way
| 2nd Order (Reverse Midrange Polarity) * fH/fL = 10 | 2nd Order (Reverse Midrange Polarity) *
fH/fL = 8 | |
|---|---|---|
| C1 | 0.0791 / ( rH fH ) | 0.0788 / ( rH fH ) |
| C2 | 0.3236 / ( rM fM ) | 0.3046 / ( rM fM ) |
| C3 | 0.0227 / ( rM fM ) | 0.0248 / ( rM fM ) |
| C4 | 0.0791 / ( rL fL ) | 0.0788 / ( rL fL ) |
| L1 | 0.3202 rH / fH | 0.3217 rH / fH |
| L2 | 1.0291 rM / fM | 0.9320 rM / fM |
| L3 | 0.0837 rM / fM | 0.0913 rM / fM |
| L4 | 0.3202 rL / fL | 0.3217 rL / fL |
| Bandpass Gain 2.08db | Bandpass Gain 2.45db |

Figure 5 - 3-Way 12dB/ Octave Crossover
3rd Order 3-Way
| 3rd Order Normal Polarity * fH / fL = 10 | 3rd Order Normal Polarity *
fH / fL = 8 | |
|---|---|---|
| C1 | 0.1138 / ( rH fH ) | 0.1158 / ( rHf H ) |
| C2 | 0.2976 / ( rH fH ) | 0.2927 / ( rHf H ) |
| C3 | 0.0765 / ( rM fM ) | 0.0884 / ( rMf M ) |
| C4 | 0.3475 / ( rM fM ) | 0.3112 / ( rMf M ) |
| C5 | 1.068 / ( rM fM ) | 0.9667 / ( rMf M ) |
| C6 | 0.2127 / ( rL fL ) | 0.2130 / ( rL f L ) |
| L1 | 0.1191 rH / fH | 0.1189 rH / f H |
| L2 | 0.0598 rM / fM | 0.0634 rM / f M |
| L3 | 0.0253 rM / fM | 0.0284 rM / f M |
| L4 | 0.3789 rM / fM | 0.3395 rM / f M |
| L5 | 0.2227 rL / fL | 0.2187 rL / f L |
| L6 | 0.0852 rL / fL | 0.0866 rL / f L |
| Bandpass Gain 0.85db | Bandpass Gain 0.99db |
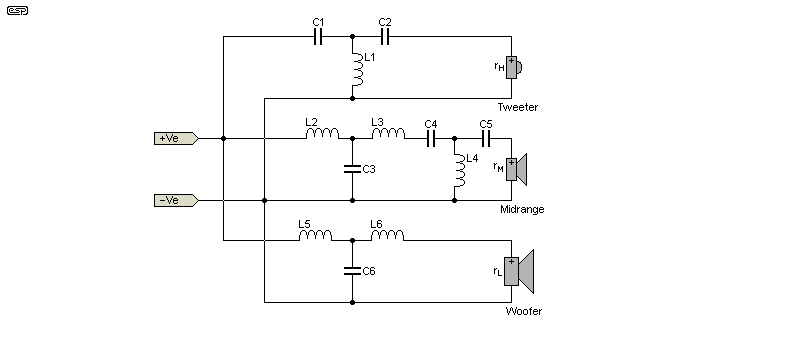
Figure 6 - 3-Way 18dB/ Octave Crossover
4th Order 3-Way
| 4th Order Normal Polarity * fH / fL = 10 | 4th Order Normal Polarity *
fH / fL = 8 | |
|---|---|---|
| C1 | 0.0848 / ( rH fH ) | 0.0849 / ( rH fH) |
| C2 | 0.1686 / ( rH fH ) | 0.1685 / ( rH fH ) |
| C3 | 0.3843 / ( rM fM ) | 0.3774 / ( rM fM ) |
| C4 | 0.5834 / ( rM fM ) | 0.5332 / ( rM fM ) |
| C5 | 0.0728 / ( rM fM ) | 0.0799 / ( rM fM ) |
| C6 | 0.0162 / ( rM fM ) | 0.0178 / ( rM fM ) |
| C7 | 0.2523 / ( rL fL ) | 0.2515 / ( rL fL ) |
| C8 | 0.0567 / ( rL fL ) | 0.0569 / ( rL fL ) |
| L1 | 0.1004 rH / fH | 0.1007 rH / fH |
| L2 | 0.4469 rH / fH | 0.4450 rH / fH |
| L3 | 0.2617 rM / fM | 0.2224 rM / fM |
| L4 | 1.423 rM / fM | 1.273 rM / fM |
| L5 | 0.0939 rM / fM | 0.1040 rM / fM |
| L6 | 0.0445 rM / fM | 0.0490 rM / fM |
| L7 | 0.2987 rL / fL | 0.2983 rL / fL |
| L8 | 0.1502 rL / fL | 0.1503 rL / fL |
| Bandpass Gain 2.28db | Bandpass Gain 2.84db |
The 4th order network circuit is not shown, as its complexity is such that 4th order networks are best achieved using active filters. High order passive filters are not recommended, and an active system should be considered first.

| Figures 1 through to 6 are based on the drivers appearing purely resistive, using networks shown in Figure 7. If impedance compensation isn't used, the tables will give answers that may make some sense, but only if the actual impedance at the crossover frequency is used, and not the driver's nominal impedance. Actual performance is something of a lottery unless you are prepared to do a fair bit of adjustment after the system is assembled. |
Please be aware that although the utmost care has been used to create these tables, there may be errors - particularly with the constants used for each formula. Because of the repetitious nature of these data, it's very easy to 'misplace' a digit, and that will affect the outcome of the formula. Also, it's essential to use the correct configuration for the midrange filter. If the order of the low-pass and high-pass filters is changed, you may get more pass-band ripple (deviations from flat for the summed response). With care, it should be possible to get the summed response to have no more than ±0.5dB ripple, and it's unrealistic to expect it to be much better.
It's a point I've made countless times, but you only have to look at a 3-way 4th order passive crossover to see that it will be very expensive to put together. Not only do you have the crossover components, but you also require impedance compensation for the drivers or the results will be unpredictable (and rarely in a good way). The filters are sensitive to even small variations, and if you also consider voicecoils heating up during loud passages (or if you listen at high volume) then the crossover is messed up quite badly. This happens even with small changes - just a couple of ohms can make a surprisingly large difference.
The only sensible approach to high-order crossovers is to use active circuits. Yes, you need an amplifier for each driver, but these are easy (and comparatively cheap) to build yourself, and the end result will be a no-compromise system. You don't need any impedance compensation, and the compete system will outperform any passive network. There's zero power loss in inductors or resistors, damping for the woofer is not compromised, and the crossover frequencies don't change if a voicecoil gets hot. There is still a loss of level (because the impedance is higher), but this is a minor side-effect when compared to the major changes that occur with a passive network.
Because speaker drivers are reactive, they have impedance, not resistance over the audio range. This means that the load presented to an amplifier or crossover network is frequency dependent, as shown in any impedance curve you wish to examine. For a passive crossover to work correctly (with the sole exception of a 2-way, first-order series network), the drivers must be made to appear resistive, for a range of at least 1.5 octaves (preferably 2 octaves) either side of each crossover frequency. The following circuits are used, assuming a 3-way system.
The required design processes for impedance compensation is not shown here. They are described in detail in the companion article Impedance Compensation For Passive Crossovers.

Figure 7 - Impedance Equalisation Networks
The important thing to note is that the above drawing shows only the impedance compensation networks. The crossover network is in addition to what's shown, adding even more parts. It is possible (at least in theory) to build a crossover that doesn't require full compensation, but it will be an empirical (i.e. trial and error) process. Some people will be better that this than others, and there are various computer programs that may be able to produce a design, provided all driver characteristics are known (and are accurate). It's almost certain that the final design will still need some adjustments, because speaker parameters will change depending on the enclosure size, damping applied or even panel resonances.
In general, tweeters almost always need a notch circuit to flatten the resonant peak (usually somewhere between 700Hz to 1.2kHz or so), and rarely need a Zobel network because the voicecoil inductance is generally quite low. Midrange drivers require a Zobel network to flatten the impedance at higher frequencies. An L-Pad is generally required to reduce the tweeter level to match the woofer or mid-bass driver.
A notch filter is necessary if the midrange resonance is less than two octaves from the bass-mid crossover frequency. For example, for a 300Hz crossover frequency, the midrange resonance (in its enclosure) should be no higher than 75Hz. It may be possible to use a simplified circuit to suppress the resonant peak, but that's not something I'd count on. An L-Pad is almost always necessary for 3-way systems, because the filter network provides up to 2dB of 'gain' for the midrange output. An L-Pad should not be used on a mid-bass driver.
Woofers (or mid-bass drivers in a 2-way system) only need a Zobel network to counteract the impedance rise due to voicecoil inductance. There is no requirement for a notch network to equalise the woofer/ mid-bass resonant peak, and even attempting it is futile. Very high values of capacitance and inductance are needed, which will add significant cost for no good purpose. While it may make the electrical impedance look 'nicer', it will not change the acoustic performance of the woofer in any way.
If you can manage to obtain perfectly flat impedance response across the range for each driver, the results will be very good indeed. However, the values of all crossover components are critical, and the formulae shown don't take inductor resistance into consideration. This will always reduce the sensitivity of midrange drivers and woofers. It's essential to measure the sensitivity of the drivers in the enclosure they are intended for, as everything makes a difference. The resonant frequency of mid-bass, midrange and woofers is affected by the enclosure and the amount of acoustic fill used. If the final sensitivity isn't measured, it will be very hard to get the L-Pad calculations right. For a calculator to work out the values needed for L-Pads, see Loudspeaker L-Pad Calculations.
Note that none of these networks are required with an active system, because speaker impedance cannot influence the crossover network's performance.
Despite initial appearances, this article is intended to dissuade prospective loudspeaker builders from using passive networks. It's fairly easy to see that the complexity of passive networks is much higher than often expected, and the final cost will reflect this. Few commercial loudspeaker systems incorporate everything described here into their designs, and that's the result of the primary goal - to build a system that can be sold at a reasonable profit. Usually, you can expect the manufacturer to have spent hundreds of hours testing various combinations of driver and crossover parts to arrive at a product that will satisfy buyers (and reviewers!) within its price range.
There may well be exceptions to the basic comments above, and it's quite easy to spend well in excess of $100k for a pair of 'top-of-the-line' loudspeakers. It's expected (or at least hoped) that if you spend that much, you should be getting the best of everything, but that's not necessarily the case. Some manufacturers rely on their reputation to justify sky-high prices, and may cut corners just like their lesser rivals. Unless you have access to the crossover networks or at least a schematic, you don't know. Likewise, you also need to know the Thiele-Small parameters for all drivers used, because they dictate the impedance equalisation that's required to get a flat impedance across the crossover frequencies.
With enough time, patience and test gear, it's possible to 'tweak' a crossover network so that it deliberately incorporates driver characteristics to arrive at a final system that isn't so complex that it would make the system unaffordable for the target market. Some may not even bother too much, and will sell the system with claims of 'magic' performance, 'musicality' or just a few naughty fibs about its 'superlative' performance. It's notable that no loudspeaker manufacturer will ever tell you about any limitations, and everyone seems to perpetually keep making the 'world's best' system. Frequency response graphs may be created by using excessive 'smoothing' so you don't see the amplitude variations, and other may take an average of multiple tests from different angles. The number of loudspeaker systems that all lay claim to glory is astonishing, and loudspeakers are still the weakest link in the audio chain. Differences are (usually) clearly audible, even with designs from the same manufacturer.
You'll often see references to 'voicing' a system, meaning that it's been tweaked by the designer so it sounds the way s/he likes it. Some listeners/ reviewers will agree, others will disagree. As a result, you'll see a great many crossover schematics that seem far too simple to be effective, but they can still be made to sound good to the average (and often above-average) listener. When an L-Pad is used to attenuate the tweeter, the requirements of the notch circuit are relaxed, because the parallel resistance reduces the amplitude of the impedance peak. There are also other tricks that can be used (such as configuring a high pass filter to act as a 'bridged-T' network), along with using the driver's characteristics to advantage. Most such networks will only work with the original drivers used in the design, and substitutions will often cause the system to be changed - often dramatically, and almost always for the worse.
With a fully active system, a driver change only needs a small adjustment to account for different sensitivity. Because no impedance compensation is needed, a replacement driver should manage to sound much the same as the original, provided it has equivalent frequency response, cone rigidity and freedom from 'artifacts' that cause colouration (bass drivers are an exception, especially when used in a vented enclosure). With a passive system, the impedance compensation networks will almost always need to be changed, and the crossover may need to be altered as well if the equalised impedance is not identical to the original. This seriously limits your options for exchanging drivers, because there are so many interdependent factors that come into play.
My recommendation will always be for an active system, but just biamping can be a major improvement over a full passive crossover. This means separate amps for the woofer and mid+high sections, with a passive network between the midrange and tweeter. It eliminates the very large (and expensive) parts needed for the low-frequency crossover network, and the changes needed if you want to use a different midrange or tweeter are minimised. No, it probably won't match a fully active system, but it's a viable alternative to a complete 3-way (or, perish the thought, 4-way) passive crossover.
Other references are from ESP articles, which cover a wide range of options. Projects include Project 09 (stereo 24dB/ octave 2-way active crossover) which can also be configured for 12dB/ octave, and Project 125, a 4-way 24dB/ octave crossover (two for stereo).
 Main Index
Main Index
 Articles Index
Articles Index