
 |
| Elliott Sound Products | Impedance Compensation |
 Main Index
Main Index Articles Index
Articles Index Speaker crossover networks are always a requirement with any system using two or more loudspeaker drivers. The Design of Passive Crossovers article covers 12dB/ octave types in considerable detail, and shows just how complex it is to get a good result. While some high quality systems go to great lengths to get everything right, many don't, so the result is not always as expected (or hoped for). There is also some information on 6dB/ octave crossovers, but in many circles they have a bad reputation.
For passive crossovers, the network is designed to match a resistive load across the crossover frequencies. Loudspeaker drivers are (with few exceptions) not resistive, but are reactive. They are truly resistive at two frequencies, resonance, and at the lowest impedance seen on the impedance curve. Examples are shown below. The differences aren't subtle looking at the electrical performance, but may be less noticeable in listening tests. The basics are covered in the article Design of Passive Crossovers (and the reference below), but the explanations there look at both the crossover and impedance compensation. This article deals solely with the latter.
My preference is for active crossovers, but for a simple system this is often difficult to justify. The cost penalty isn't great, but it adds complexity and means a four-wire connection is needed for the speaker. This isn't sensible for a simple 2-way box that is used at low power, and it doesn't suit some speaker builders who don't want to have to use multiple amplifiers. There will always be reasons (some good, some not-so-good) that a constructor will want a system that can be driven by a single amp.
An example of just such a system is shown in Project 73 (Hi-Fi PC Speaker System), and that shows a 6dB/ octave series crossover network. This has been in daily use for nineteen years (at the time of publication of this article), and has seen several different PCs in its time. Apart from one repair (a faulty electrolytic capacitor in the power supply), the system hasn't missed a beat in all that time!It's worth noting that the first-order (6dB/ octave) crossover is the only version that works best (or at least better) when connected as a serial network. In general, higher order serial crossovers become unwieldy and very sensitive to component variations, including voicecoil resistance. This is covered in some detail in the ESP article referenced above, and serial connection is not recommended for 12dB/ octave or above. As part of my workshop monitoring system, I use a simple vented 2-way box with a series 6dB/ octave crossover. It doesn't match my horn-loaded 'main' system (fully active), but it does let me make direct comparisons of power amplifiers, and it sounds fairly good overall.
This article has many similarities with the Series vs. Parallel Crossover Networks article, but is specifically aimed at impedance compensation, and crossover details are not covered. There is plenty of other information on the ESP site that looks at crossover design in general, and the crossover design follows the impedance compensation process. You can't design a crossover until the final (and hopefully resistive) impedance has been done with appropriate networks.
With higher order crossovers (12dB/ octave or 18dB/ octave) impedance compensation is mandatory if you want a final system that performs well. In many cases this point is not made clear (or may not even be mentioned!). If you expect to build a fully compensated 3-way crossover (12dB or 18dB/ octave), be prepared for a world of pain - these networks become very complex, very quickly. The cost is likely to be such that using an active system (provided you build your own active crossovers and amplifiers) will be cheaper and will perform far better. This is especially true if you intend to use 4th order (24dB/ octave) filters. Not only are you up for the cost of eight expensive inductors and capacitors (just for the crossover!) the circuit sensitivity to any variation is high, and impedance compensation still can't cope with voicecoil temperature changes.
I selected a tweeter and mid-bass driver from my 'stash', and ran an impedance test on them, as well as determining their free-air parameters. The plots are shown for each driver, and provide the impedance and phase response.

I don't know the origin of the C3084 mid-bass driver, as I've had it lying around for many years. At some point, the cone was 'doped' to change its characteristics, and I don't have an original (unmodified) driver to compare it to. However, it's impedance plot is at least representative of typical drivers used in the role.
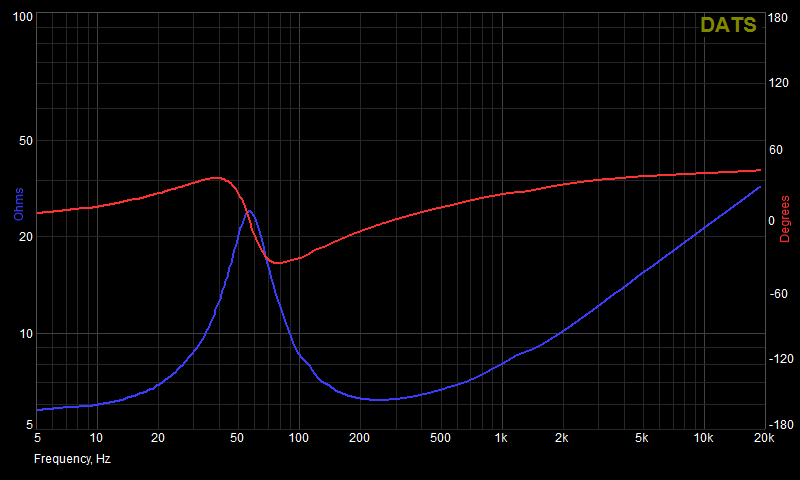
To use an impedance correction network for any speaker driver, you must measure the parameters - it can be done from the impedance curves as shown, but determining the values needs would be irksome at best. This can be done in a number of ways, and you can use the technique described in the article Measuring Loudspeaker Parameters. I used the DATS system to provide the basic parameters as shown below. There's no point trying to obtain Vas (equivalent air volume of suspension), and it's not required for compensation networks.
fs Resonant frequency Re Voicecoil resistance Zmax Maximum impedance Qms Mechanical Q Qes Electrical Q Le Voicecoil Inductance
As described below, these parameters are used to calculate the equivalent circuit of the tweeter and woofer/ mid-bass drivers, from which you can devise impedance correction networks. The calculations that follow use the data for the two drivers shown above. Yours will be different, but the figures are representative.
Vifa D26G-05 Tweeter fs 1425 Hz Re 4.542 Ohms Zmax 8.239 Ohms Qms 1.105 Le 886 µH (This is obviously not correct, and needs to be calculated. I used a value of 57µH) Qes 1.325 Qts 0.6025 (Total Q - Not used)
C3084 Mid-Bass fs 57.2 Hz Re 5.637 Ohms Zmax 25.35 Ohms Qms 2.885 Le 901 µH (This value [kind of] works, but is difficult to model accurately) Qes 0.8251 Qts 0.6416 (Total Q - Not used)
The Qts isn't used, but the measurement system gave it to me anyway, so it's included for reference. Figure 1 shows the equivalent circuits of a woofer (or mid-bass) and tweeter, and the figures for your drivers can be substituted for those shown. Note that the parallel resistance (representing losses) is Zmax minus Re. With the figures shown above, that makes the parallel resistance 25.35 - 5.637 Ohms (19.713Ω). 20Ω is close enough.
Using the formulae shown below, the effective inductance is 989µH, with a parallel capacitance of 16.75µF. These figures are close to those shown for the hypothetical driver I used in the calculations, and shows that the techniques used are accurate enough for our calculations (assuming that you use impedance compensation). The voicecoil (semi) inductance is somewhat higher than expected, and the measured value doesn't correlate with the impedance curve. It's a semi-inductance, and this is not provided by the measurement system I used. I also suspect that the tweeter isn't 'quite right' (I did say that it's old and decrepit  ). Otherwise, a simulation using the values calculated is almost a perfect match for the measured parameters.
). Otherwise, a simulation using the values calculated is almost a perfect match for the measured parameters.
This information is far more useful (and essential) when calculating the values for more complex (higher order) crossovers, which are more sensitive to variations in speaker impedance across the crossover region. Even a comparatively small impedance change can cause serious disturbances to the overall frequency response. By modelling the drivers accurately, you'll get a better overall result than simply assuming that the impedance remains constant. It doesn't for the vast majority of moving coil loudspeaker drivers.
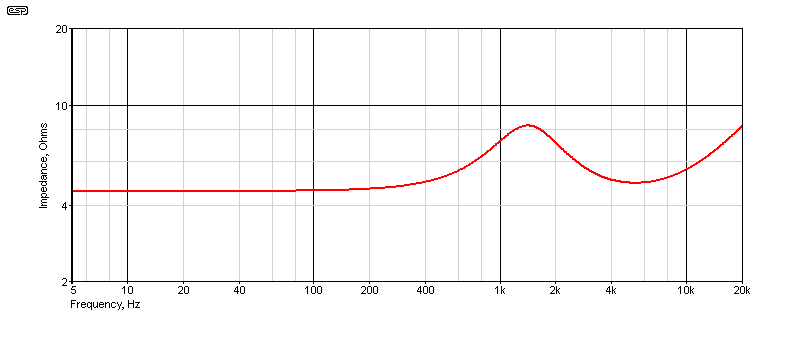
The equivalent circuit for drivers is not especially difficult to calculate when you have the Thiele-Small parameters listed above. First, you need to determine the maximum impedance (the simulated version in Figure 2 shows a peak of 28.2 ohms). You may be able to get this from the datasheet. You can now determine the apparent capacitance and inductance of the diaphragm and suspension. Remember that the equivalent parallel resistance is in series with the voicecoil resistance. At resonance, the capacitance and inductive reactances are equal. The mechanical Q (Qms) of the system modifies the formulae, and should be used if available. For the tweeter, I've assumed Qms to be 2, which is likely to be fairly realistic. That's how the values shown for the tweeter were calculated. I don't claim that this process is exact, but it does give results that are very close. Naturally, if you measure the drivers carefully you can determine Qms and get a near perfect result.

When we compare the performance of the two equivalent circuits above to the plots, and you'll see that they are close to being identical. Impedance plots for each are shown below the relevant section. Impedance compensation hasn't been applied for either driver yet, and that will follow in the next section.
First, the starting value for XL is determined. This value sets the impedance peak, in this case to a total of 8.239Ω. First, we have to subtract the electrical resistance (re) of 4.542Ω. This leaves us with the value of XL, at 3.867Ω.
XL = 2π × fs × L Where XL is inductive reactance L = ( XL / Qms ) / ( 2π × fs ) L = ( 3.867 / 1.105 ) / ( 2π × 1425 ) 391µH
The solution to find the inductive part of the mechanical system (the moving mass) is shown above, and below is the formula to find the capacitive part (corresponding to the compliance). Tweeters that use ferro-fluid usually have a fairly well-damped resonance, with the impedance only rising to perhaps double the nominal value. Some others can be quite radical, and are more likely to create problems.
XC = 1 / ( 2π × fs × C ) Where XC is capacitive reactance C = 1 / ( 2π × fs × XC / Qms ) C = 1 / ( 2π × 1425 × 3.867 / 1.105 ) 32µF
Having worked out likely-looking values, a sanity check is necessary to make sure that errors didn't creep in (which can be surprisingly easy). The sanity check is simply to work out the resonant frequency of the L/C network we calculated. It should be very close to the measured resonant frequency (within 1%).
fs = 1 / ( 2π √ ( XL × XC )) f = 1 / ( 2π × √ ( 391mH × 32µF )) 1,423 Hz
That's only 2Hz off the measured resonant frequency, so we're all good  .
.
Next, we'll do the same for the mid-bass driver.
XL = 2π × fs × L Where XL is inductive reactance L = ( XL / Qms ) / ( 2π × fs ) L = ( 19.7 / 2.885 ) / ( 2π × 57.2 ) 19mH
The solution to find the inductive part of the mechanical system (the moving mass) is shown above, and below is the formula to find the capacitive part (corresponding to the compliance).
XC = 1 / ( 2π × fs × C ) Where XC is capacitive reactance C = 1 / ( 2π × fs × XC / Qms ) C = 1 / ( 2π × 57.2 × 19.7 / 2.885 ) 407µF
We'll run the sanity check again, to verify that the calculated values for L and C are correct, although we don't really need these to determine the Zobel network. The important part is Le, the voicecoil inductance. For reasons that I do not understand, the DATS measurement system gets this wrong every time, so it has to be corrected.
fs = 1 / ( 2π √ ( XL × XC )) f = 1 / ( 2π × √ ( 19mH × 407µF )) 57.24 Hz
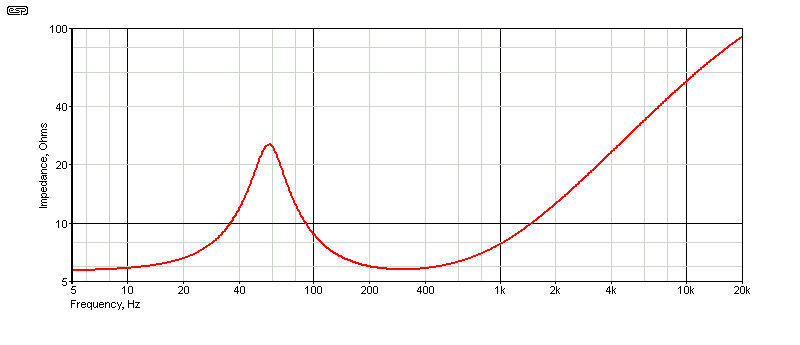
Figure 5 - Simulator Plot of C3084 Mid-Bass
This is also well within tolerance, (±1%). You don't really need to worry about the mid-bass driver's resonance, because it's well away from the crossover frequency and doesn't influence the performance. Be aware that these calculations are approximate, and the actual values may be somewhat different. This is especially true of the voicecoil's inductance, which the measurement system got wrong for both drivers. Unfortunately, it's difficult to calculate the value because it's a semi-inductance and is quite hard to model without a great deal of hassle.
The same formulae will be used to calculate the impedance correction network, but the resistance value used is the voicecoil resistance (Re). The series resistance is then selected empirically, to obtain the flattest possible impedance. It should be possible to obtain a resistive load with less than ±0.2Ω deviation, as shown in the next section.
The woofer needs a compensation network (series resistor/ capacitor) to ensure that the impedance doesn't rise due to the voicecoil's inductance. While it is possible to calculate the capacitance needed, it's far easier to use a test box to determine the optimum resistance and capacitance. In theory, the resistor will be the same value as the voicecoil's resistance, but in reality it will usually be a bit higher. If this network is not included, the woofer or mid-bass driver's impedance will rise with increasing frequency, and that upsets the crossover network which can no longer provide a flat summed output.
Although I included the full equivalent circuit for the mid-woofer in the next section, you only need to know the DC resistance (Re) and the inductance (or semi-inductance) of the voicecoil (Le). There's no requirement for a compensation network to reduce the resonant impedance peak unless the system is 3-way and the bass-mid crossover frequency is close to the midrange driver's resonant frequency.
Impedance compensation networks are essential for most passive crossover networks. Without these networks, the crossover doesn't see a resistive load, and that causes the response to deviate from the ideal. The tweeter is the hardest to deal with, because it requires a perfectly complementary notch circuit to effectively cancel the tweeter's resonant peak. This network requires a resistor, capacitor and inductor. Expecting perfection is (usually) unrealistic, but if the impedance can be made to deviate by less than ±1Ω, there will be very little disturbance to the crossover network. Most speakers have a multiplicity of small peaks and dips, rooms add even more, so small variations due to imperfect impedance compensation are usually of little consequence.
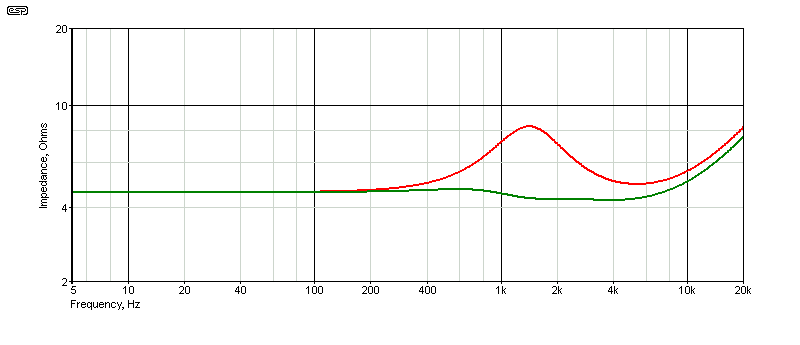
This tweeter is a little unusual, because it has a very small impedance peak, but comparatively high voicecoil inductance. Ideally, you'd also include a Zobel network to just reduce the impedance at 12kHz, but in reality no-one would bother. The corrected impedance is only 0.38Ω higher than the median value at 750Hz, and at 3kHz the impedance is 4.25Ω (this is the design impedance for the crossover network). At 12kHz, the impedance has risen to 5.52Ω and this is unlikely to cause any problems.
Many other tweeters have much higher impedance peaks, and somewhat perversely, it's likely to be easier to get a very good compensation network with these than with well damped tweeters. Each case is different, and even drivers of the same brand and model can be slightly different.
Most woofers and mid-bass drivers require a Zobel network to prevent the impedance from rising above around 200-300Hz (this varies with the driver). The voicecoil (semi) inductance is responsible for the impedance increasing, and a simple series R/C (resistor/ capacitor) network is placed in parallel with the driver. This is a Zobel network, and it's designed to prevent the impedance from rising at high frequencies. Adding the network does not change the performance of the driver.
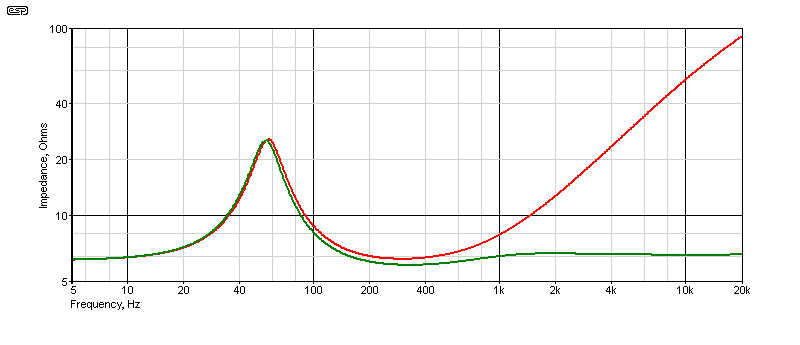
The impedance change between 750Hz and 12kHz (two octaves) is less than 0.4Ω, referred to a 3kHz crossover frequency. There's a small dip at 750Hz (0.39Ω), and there's less than 0.1Ω change between 1.5kHz and 6kHz. That means the crossover network sees an almost perfectly resistive load across the frequency range of interest. The impedance falls by less than 1Ω even at its lowest point (300Hz), and remains within 1Ω down to 112Hz. The average impedance is 6.12Ω, and that's the value that must be used when designing the crossover.
All speakers have the same basic components that provide an equivalent circuit as shown in Figure 3. Voicecoil resistance is measured at 25°C, but it increases with temperature. The semi-inductance is difficult to measure directly, but it can be determined using a frequency-sweep, which will show the impedance rising beyond the minimum value measured (which is usually close to the voicecoil resistance (Re). You can calculate the approximate inductance, or use a speaker test box (such as that shown in Project 82 - Loudspeaker Test Box. This is a great deal easier than calculation, and gives a near-perfect result.
Once impedance compensation is added, the impedance across the crossover range (crossover frequency, ±1 octave minimum) should remains flat for both drivers. It's unrealistic to expect it to be perfect, but ideally the impedance variation should be less than 10% of the combined driver and its impedance compensation network. If the crossover frequency is 3kHz, then we want the impedance to remain constant from 1.5kHz to 6kHz. If this can be extended to ±2 octaves (750Hz to 12kz) that will improve the response.
The next step is to determine the values for the compensation networks. This can be done with a simulator (as shown here) or by testing. Determining the Zobel network is easy with the Project 82 test box, but the notch filter for the tweeter has to be calculated. It's almost guaranteed that you will need to adjust some of the values, and the end result is very much a compromise. The art of compromise is the difference between excessive complexity and performance, and loudspeaker systems push it to the limits.

The next step is to determine the impedance equalisation values. The mid-bass Zobel network is the easiest, so we'll do that first.
The details of the mid-bass driver are shown again so you don't have to refer to the beginning of the page. Because we don't need to equalise the bass resonance, there are only a few parameters required, and the ones we don't need have been removed ...
Re = 5.637 Ohms Le = 901 µH (This value works, although it seems much higher than expected)
Determining the Zobel values is pretty simple if you stay with the maths, but is even easier with the test box referred to above. There are several different ideas in the wild, but my preferred formulae are ...
RZ = Re × 1.1 Where RZ is the Zobel resistance CZ = Le / RZ² Where CZ is the Zobel Capacitance
If we work these figures for the mid-bass unit's parameters, we get a Zobel resistance of 6.2Ω and a capacitance of 23.47µF. A simulation shows that this network flattens the impedance curve rather well. The graph shown in Figure 7 was obtained with a capacitance of 22µF, a little less than the calculated value. Even though the DATS tester showed 901µH (which appears to be far too high), it does make the formula work. This is why the test box is much easier than calculation or simulation, and it gives exact results.
I ran the mid-bass driver with a sweep waveform and used my test box to check the optimum values. Unsurprisingly, it gave a very similar answer, and it's one that I can trust implicitly because it's a real test with real components. The optimum Zobel network turns out to be 22µF in series with 6.9Ω. The correlation is better than I expected, demonstrating that the methods described do work (this includes the alternative method described a bit further down).
Notch filters to equalise the tweeter's resonant peak are a bit harder, and a test box isn't really feasible. The key parameters are the resonant impedance, voicecoil resistance and the driver's Qms, and while the first two are easy to determine, Qes either has to be measured or estimated. Few tweeter specifications include it, and it will almost always need to be measured. For the simulated drivers described here, Qes is about 0.8 and for this example I'll use that figure.
RN = Re / Qes Where RN is the notch filter resistance
Determining the notch filter inductance and capacitance requires a bit of faffing around. While it is covered in the Design of Passive Crossovers articles, it's repeated here for convenience. Firstly, you need to obtain the -3dB frequency (f3) of the driver's impedance, and then capacitance and inductance are calculated from the formulae ...
C = 1 / ( 2π × Re × f3 ) L = 1 / ( 4π² × fs² × C )
The details of the tweeter are shown again so you don't have to refer to the beginning of the page ...
Substituting our tweeter, we will obtain the following ...
Re = 6.713 Ω fs = 1425 Hz ZMAX = 8.329 Ω f3 = 630 Hz Qms = 1.105 Qes = 1.325
RN = 6.713 / 1.325 7.75Ω CN = 1 / ( 2π × 6.2 × 630 ) 37 µF LN = 1 / ( 4π² × 1425² × 37µ ) 390 µH
Note that RN is the sum of the external resistance plus the inductor's resistance. If the inductor has a resistance of 1.5Ω, the external resistance is 6.25Ω. The impedance is as flat as can reasonably be expected, varying by less than ±1Ω across the crossover frequency range (625Hz to 10kHz, allowing ±2 octaves either side of the crossover frequency).
 | Note that the value for the notch resistor is the total resistance. The value of RN is the sum of the notch resistance and the resistance of the inductor (LN). If you fail to reduce RN to compensate for the inductor's resistance, the notch won't work properly. RN is therefore equal to the calculated value, minus the resistance of LN. This can be expected to be around 0.5Ω, but it has to be measured carefully. The external resistance won't be a standard value, and will almost always require series or parallel resistors to get the value required. There's a lot to be said for winding the coil yourself, using wire that's thinner than normal, as this reduces the amount of external resistance required. |
Alternative formulae have been devised by Vance Dickason (editor of Voice Coil magazine and several books, in particular the 'Loudspeaker Design Cookbook'), and you can use them instead of those I devised if preferred. The Zobel network for the mid-bass is determined by the following ...
RZ = Re × 1.25 7.0Ω CZ = Le / RZ² 18µF
This gives a better correlation with the test box figures for the resistance, but the capacitance is too low, even when using the full DATS computed value for Le. The test box remains the preferred method, because it's an empirical technique that will always get the right answer (with a bit of care of course).
For the notch filter, Dickason suggests ...
RN = Re + (( Qes × Re ) / Qms ) 14.8Ω CN = 1 / ( 2π × fs × Qes × Re ) 12.56µF LN = ( Qes × Re ) / ( 2π × fs ) 993µH
The values are different, but the end result is fairly similar to the version I suggest. However, the overall impedance is a little higher and there's also more impedance 'ripple' within the 1.5kHz-6kHz range. That gets a bit worse when the range is extended from 750Hz to 12kHz. It's probable that the difference would be audible in an A-B test, but in reality both versions are 'good enough'. The fussy constructor may choose to finesse the values to get a better result, but most probably wouldn't bother.
It's common for the tweeter to be more sensitive than the mid-bass, and it often needs some attenuation. You don't always need to be fussy about maintaining the correct impedance, because the crossover network will be designed to use the actual impedance of the complete sub-circuit (L-Pad, impedance compensation and the driver itself), and the necessary level reduction can just be a series resistor, selected to attenuate the tweeter by the required amount. For example, if the tweeter is 3dB more efficient than the mid-bass, just placing a resistor in series with the tweeter (and notch circuit) will provide the attenuation required. However, using an L-Pad helps to suppress the resonance due to the parallel resistor, so the notch circuit is not quite as critical.
Rather than repeating everything here, refer to the article Loudspeaker L-Pad Calculations, which covers the topic in detail. It includes a simple calculator that you can use to maintain the desired impedance while providing the attenuation needed. Mostly, you don't need to go overboard, especially with a series network. However, for the L-pad to work properly, it's helpful if an impedance compensation network (a notch filter) is used to keep the impedance constant.
Things can get 'interesting' if the system is driven fairly hard. I don't know how many readers have ever tried to hold a 10W resistor when it's dissipating 10W, but it will be uncomfortably hot. So much so that you will be burned if you try to hold on to it for very long (more than a couple of seconds). A voicecoil is no different, and indeed may be worse because there's less thermal mass. While most woofers have some ventilation, it's not great, and over 97% of all power delivered to most speakers is dissipated as heat. If the woofer's voicecoil resistance increases to 11Ω (a voicecoil temperature of a bit over 200°C), all the impedances presented to the crossover network are altered. Given the sensitivity of passive crossover networks to impedance variations, it stands to reason that response changes are inevitable.
Because of the number of different passive network designs, it's rather pointless to try showing any examples. However, if you model the complete system in a simulator, you'll be able to see how the response is affected. It will never get any better, unless you specifically designed the crossover to handle higher impedances due to hot voicecoils. Of course, that means that the response will not be correct when the system is run at lower power. This is another compromise.
There's a great deal of complete nonsense on the Net about the 'audibility' of certain components, and capacitors seem to be the most commonly discussed parts. However, a frequency response test (under load) will quickly show that there is almost no difference between any two capacitors with the same ratings (in particular, capacitance and voltage). You can set up a null tester quite easily to prove to yourself that this is the case. While it's well outside the scope of this article to describe such a tester, you don't really need one. Choose good quality (but not necessarily 'audiophile') parts, with a generous voltage margin, and preferably with a low ESR (equivalent series resistance). This usually doesn't change by very much with most capacitors.
Polypropylene is generally the preferred dielectric, as it has low losses. This is important when a capacitor has to carry several amps of current at higher audio frequencies. In some cases, it may be cheaper to get 'motor start/ run' caps, especially when high capacitance is needed. While it might seem unlikely, polyester (aka Mylar® or PET) caps are also fine, provided they are rated to carry the current demanded by the drivers.
Bipolar electrolytics should be your last choice, and only if you can't get anything else. They have a finite life, much higher ESR than most film caps, and usually have limited current ratings. Be careful when you see claims that a capacitor's dissipation factor is a major factor in 'the sound'. Very few film capacitors have a dissipation factor that will cause any problems at audio frequencies, with the possible exception of bipolar electrolytic types. Even with these, it usually only becomes a problem as the capacitor ages, and that is a good reason to avoid them if possible.
Inductors are another matter entirely. As the world's worst passive component, you need to choose carefully to ensure that the DC resistance is low, and be aware of possible self-resonance. Even if it's outside the audio range, it is possible (albeit unusual) for self-resonance to cause power amplifiers some grief. There's a wide range available, with many from specialist ('audiophile') suppliers. Some of these may be very good, others can just as easily be awful - 'customer reviews' are meaningless and should be ignored (this also applies to capacitor reviews of course - many are unmitigated drivel).
The biggest issue with inductors is their DC resistance (DCR). This is present for both AC and DC, and it does two things (neither of which is desirable). When used in series with a woofer, the damping factor provided by your power amplifier is in series with the DCR (as well as the voicecoil resistance), and this reduces damping. Thin wire might make for a smaller inductor, but it will dissipate more power than a larger coil wound with thicker wire. It's a balancing act, and finding the optimum compromise isn't easy. Because of the resistance, the coil also dissipates power (as heat), and every watt 'stolen' by the inductor is a watt that doesn't get to the loudspeaker driver.
For example, if an inductor has a resistance of only 0.66Ω and handles a current of 5A (RMS, average, providing 100W into 4Ω), it will dissipate 16.5 watts. For a comparatively small component with little or no airflow, it can get surprisingly hot, and that increases its resistance even further. Copper has a positive temperature coefficient of resistance, of 0.395% per °C. At a temperature of 150°C the same coil will show a resistance increase to 1Ω. It will now dissipate 25 watts! Quite clearly, low resistance is essential.
Some high inductance coils uses a magnetic core, which reduces the size and DCR, but at the expense of linearity. Unless the core is much larger than theoretically required, it will suffer from partial saturation, and that introduces distortion. Saturation depends on current and frequency, and is worst with high currents at low frequencies. For a 'utility' speaker system that will only be used at low power, you'll probably get away with a magnetic cored inductor, but an air-cored coil is always better. However, it will almost certainly have higher DCR unless you go for something very expensive.
Resistors are generally benign, even 'standard' wirewound types. Yes, they have some inductance, but it's unlikely to cause any problems at audio frequencies. The response aberrations of almost all drivers will exceed any error cause by resistor inductance. The vast majority of resistors used in crossover networks are relatively low values, so exhibit only small amounts of parasitic inductance. Non-inductive wirewound resistors are available, but some are 'ordinary' wirewound types that have been marked (or sold) as 'non-inductive'. This is something I've tested and verified, and it's not a myth. In general, the inductance of most 'ordinary' wirewound resistors will be a few micro-Henrys, and rarely cause any problems.
The topic of component selection is covered in more detail in the Design of Passive Crossovers article.
I think that the conclusions pretty much speak for themselves. Impedance compensation is required for (almost) all passive crossover networks, and while it is theoretically possible to design a crossover that doesn't need compensation, it will be an iterative process and will be very time-consuming. For commercial designers, they will have a wide range of different components (especially capacitors and inductors) on hand, and they are in a position to be able to experiment easily. The cost of the parts is usually enough to deter most hobbyists, and they will usually try to determine the parts required before purchase. This is limiting, but I doubt that many DIY people would be able to justify several $thousand for a comprehensive range of parts.
While there are quite a few on-line crossover calculators, all rely on the speaker impedances being resistive. Even if you measure the impedance at the crossover frequency and use that value, the end result will be far from what is hoped for. The only way to get sensible results from any of these calculators is to determine the actual equalised impedance so that can be used to work out the crossover values. Many are well though out and will give good results, while others can be suspect. Unfortunately there's no way to know which is which without testing a number of different calculators and verifying that the results match.
No loudspeaker driver is free from peaks and dips, and adjacent drivers can cause diffraction, as will the edges of the enclosure. These can be hard to eliminate, and drivers should always be mounted so they are at different distances from the two sides, top and bottom. For information on cabinet bracing, vibration analysis and other aspects of cabinet design, see Loudspeaker Enclosure Design Guidelines.
One thing that you must be aware of is that all passive crossover networks rely on (close to) a zero ohm source impedance. Most transistor amps provide this, and while it's never really 0Ω, it's close enough. Very few valve (vacuum tube) amplifiers have a low output impedance, especially 'low-feedback' and 'no-feedback' designs. All passive crossovers are affected, and obtaining flat response is extremely difficult. The crossover can be designed to work properly by including accurate impedance compensation, but a non-zero source impedance will always cause problems.
Even if the driver impedances appear purely resistive, the crossover will not function normally with a non-zero source impedance. Crossovers can be designed to work with the amp's output impedance, but this is is hard to achieve. It also means that the loudspeaker will only work properly with the exact same source impedance - something of a limitation! High output impedance also limits electrical damping of the bass driver at its resonant frequency, so bass response is often exaggerated unless the enclosure is also designed for the elevated output impedance. This rather limits its usefulness.
 Main Index
Main Index Articles Index
Articles Index