

|
| Elliott Sound Products | Series vs. Parallel Crossover Networks |
 Main Index
Main Index
 Articles Index
Articles Index
Despite many of the myths that surround series networks and their acclaimed superiority over conventional parallel networks for loudspeaker design, both networks can be designed with identical transfer functions if the load impedance remains constant. Most of the claims regarding series networks are either grossly overstated or blatantly wrong and may cause deleterious effects on system performance. As with all aspects of design, there are compromises that must be made, and it is impossible to make an informed decision if you are unaware of the facts.
This article is intended to show that there are no greatly enhanced features in a series or parallel network - if properly designed their performance is essentially identical in terms of response, phase and (by extension) transient response. It is unwise to claim that one type of network is superior to the other, when simple logic dictates that if amplitude and phase response are the same, then all of the filter's other characteristics are also the same.
There are other factors than just the response, and this is where the differences between the network topologies exist. Each has good and bad points that must be considered.
Note that second order filters described here are aligned to a 'traditional' Butterworth alignment (Q = 0.707). This is because they are (or were) the most common, but the filters should be Linkwitz-Riley alignment (Q = 0.5) to prevent a 3dB peak at the crossover frequency. For full details of how to design a proper 12dB/octave passive crossover network, see Design of Passive Crossovers.
First order (6dB/octave) networks have a strong following amongst many audiophiles, and indeed, they have a number of very desirable features. They have the best possible transient response, and are predictable and easy to design, but as with all things there is a down side. The demands on the drivers are extreme, with significant power delivered to the tweeter even at its resonant frequency, and the risk of cone breakup and off-axis lobing for the mid-woofer.
Nevertheless, at low power, intermodulation products can be kept within reasonable limits with careful driver selection, and they can sound very good indeed. The test system that I used is part of my PC sound system, and although I have plenty of power available (over 25W for the satellites and 100W for the subwoofer) it's only used at low power because I tend to listen to the radio (FM) most of the time when I'm at the computer. It is not hi-fi by any stretch of the imagination, but is non-fatiguing (except for some 'music' that's played - and that's what the mute button is for).
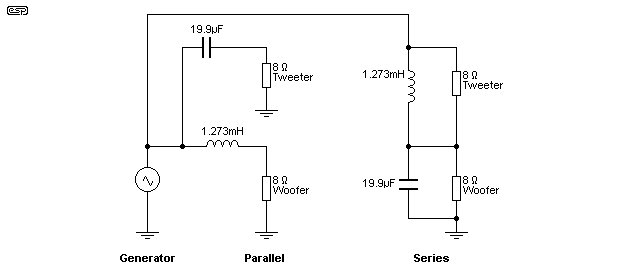
Figure 1.1 - Series and Parallel 1st Order Filters
Illustrated above are equivalent series and parallel first order crossovers with 1kHz crossover points for a fixed load. Note that resistive loads were used in order to minimise analysis variables. There is some material in the conclusion of this article describing further simulations and transient response that encompasses complex load impedances typical of a loudspeaker. 1kHz was chosen for one reason - the crossover frequency is nicely centred in the graphs for best display. The effects shown in this article are identical at any frequency.
Input impedance is exactly the same for each type, and is essentially perfectly flat, with both circuits dropping by 2 milliohms at the crossover frequency. This is of no consequence, and may be ignored.
The summed frequency response of any crossover is a good indicator of how it will sound. Electrical summing has been used for most of the tests, and that is significantly more revealing than acoustic summing from real loudspeakers. In all cases described, it's assumed that the tweeter and woofer have the same sensitivity, but in reality the tweeter will almost always need an attenuator pad that maintains the design impedance but reduces the level to match the woofer. This is not shown in any of the following drawings.

Figure 1.2 - Frequency Response and Summed Output
The frequency response and electrically summed outputs of both a series and parallel crossover network (with resistive load) are shown in Figure 1.2 and it is quite obvious that they are identical, since the graphs are perfectly overlayed (there are six graphs on the chart, not three as it appears).

Figure 1.3 - Phase Response
The phase response of the series and parallel crossovers are also identical as can be seen above. There are four graphs (two serial and two parallel) and again, they are perfectly aligned.
Figure 1.4 shows the variation of high and low pass filters and summed response when the woofer impedance is varied by ±2 ohms. Red shows the electrical sum of the variation with 6Ω impedance, and the green graph is for 10Ω. Note that only the low pass filter response is affected.

Figure 1.4 - Parallel, Variable Woofer Impedance
The results for tweeter impedance variations are similar (and affect only the tweeter section of the filter), but have not been shown, since the tweeter is far less likely to undergo any noticeable change than the woofer.
The graphs below are very interesting. The woofer impedance was again changed from 6Ω to 10Ω as was done with the parallel network. Note that although the crossover frequency moves (it becomes higher at higher woofer impedances and vice versa), the summed response remains completely flat.

Figure 1.5 - Series, Variable Woofer Impedance
The two sections have a complementary shift - when woofer impedance changes, it effects both low and high pass sections, and changes the Q of the filter sections. The result is quite obvious - unlike a parallel crossover, the response remains flat regardless of a shift in the woofer (or tweeter) impedance. If both change in any direction, the same thing happens. In theory, this means that the series network is almost immune from impedance variations in the drivers.
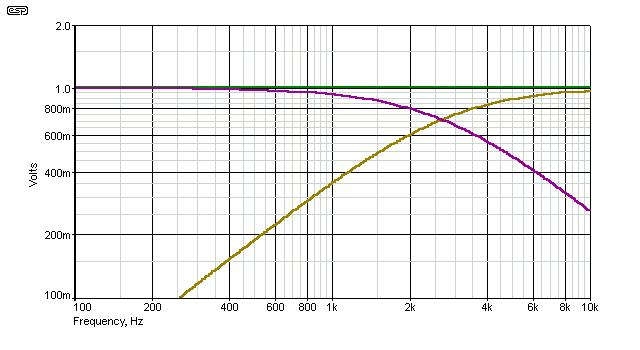
Figure 1.6 - Series, 20ΩWoofer, 3Ω Tweeter
By changing the driver impedances, two things happen. The filter Q changes, and the reflected change affects the behaviour of the other filter section. Although the individual response, Q and phase varies, the net result is that the effective crossover frequency is changed, but nothing more. This is a remarkable property, and the series first order is the only crossover filter circuit that has this ability.
Remarkable though it may be, it is still advisable to design the series network correctly, and maintain everything as close as possible to the design values. Should the woofer impedance increase (with voice coil temperature, for example), the crossover frequency will move upwards, thus providing a small measure of added protection for the tweeter at sustained high power levels.
However, all is not completely rosy. Everything in electronics is a compromise, and the selection of a crossover is no different. There is one final test that needs to be applied, and that is to examine the amount of woofer back EMF that reaches the tweeter. This is an area where the series network is inferior to the parallel.

Figure 1.7 - Series, Woofer Back EMF Attenuation
With a parallel network, only the amplifier's output impedance plus the impedance of the cable allows any cross coupling between high and low pass sections. With a zero ohm source, attenuation is infinite, and is not shown above.
A series network relies solely on the isolation of the crossover filters, and as a result, the back EMF from the woofer is not attenuated as well in a series network as it is for an otherwise identical parallel network. This may not be a major problem, since the attenuation of back EMF is similar to the attenuation of amplifier power at any given frequency (actually, it is 3dB better), and the latter is at a far greater amplitude. It is a consideration nevertheless, so be aware that it may increase tweeter intermodulation. Woofer back-EMF is not often considered, but it can have an influence on overall performance.
The series network is probably a better choice than parallel for a number of reasons. It retains a flat response even when the driver characteristics change, and is to an extent 'self correcting'. Implementation is no more difficult than for an equivalent parallel network, and the same component values are used.
On the negative side, woofer back EMF suppression is significantly worse than with a parallel network - it is up to the designer to determine if this is likely to cause a problem.
Finally, it must be remembered that any first order network dictates that the drivers will have significant power applied at frequencies where their performance will be rapidly deteriorating. However for a system that will never be operated at high power, the performance can be very satisfying. Simple 6dB/octave crossovers are uncommon except for some 'esoteric' speakers (which may include 'audiophool' types), or simple systems that are used at low power and with drivers that are suitable. The results can be very good indeed if everything is done properly.
It's not important (although it is considered 'desirable' by some) that a loudspeaker can (or cannot) reproduce a squarewave. For those who think that it is a critical factor for proper reproduction, then a first order (6dB/octave) network is the only one which can do so. It can be done with higher order filters using subtractive active filters, but the results are generally poor. Click on the link to see the article.
The design process for a 12dB/octave filter is completely different for series and parallel implementations of the same design. For a parallel network (assuming a Butterworth alignment for the sake of simplicity), the capacitance and inductance are calculated by ...
C = 1 / (2π × f × (Z × √2))
L = (Z × √2) / (2π × f)
(where Z is impedance, f is frequency, √2 is ≅ 1.414, and π is ≅ 3.14159)
A series crossover design is different in terms of the component values ...
C = 1 / (2π × f × (Z / √2))
L = (Z / √2) / (2π × f)
For this exercise, the crossover frequency was again selected to be 1kHz, and 8 ohm resistive loads were used. The series network has the advantage of using smaller inductance values, but capacitor values are higher. The difference is unimportant, but capacitors for crossovers are often more expensive than inductors. This is a minor point if there is an improvement in performance.
The values used for the simulations were as follows ...
| Common Values | Parallel Crossover | Series Crossover | |
| Crossover Frequency | 1kHz | C = 14.07 µF | C = 28.13 µF |
| Speaker Impedance | 8 Ω | L = 1.8 mH | L = 900 µH |

Figure 2.1 - Series and Parallel 2nd Order Filters
The inductors for both series and parallel networks are assumed to have a DC resistance (DCR) of 800mΩ (0.8 ohm) for convenience, but this will (probably) not be the case in reality.
As with the previous example using a first order filter, when properly aligned, the response is identical. Because the plots look exactly the same as the previous example (other than the rolloff slope), there is little point displaying graphs that show two sets of curves that are perfectly matched.
It can be stated that if two filters, regardless of topology (series, parallel, active or passive) have an identical frequency response, then they must also have identical phase and impulse responses, since these cannot be separated.
Of course, this only holds true as long as the source and load impedances are also identical. Input impedance of both filters is essentially completely flat, having a variation of only 4.6 mdB (i.e. 0.0046 dB). Due to rounding errors in the component values, there is a tiny variance between the two filters, however it is completely insignificant (about 0.17 Hz difference).
One thing that should not be overlooked is the inductor's resistance. While this causes a small loss of level with a parallel crossover network *, it will cause the series network to 'shelve' the tweeter rolloff. As a result, a DC resistance of (say) 800mΩ will cause the signal applied to an 8Ω tweeter to drop to a minimum of just over 20dB below the applied signal regardless of frequency! This includes DC under amplifier fault conditions.
There is virtually no difference between series and parallel at about 1 decade below crossover (i.e. 1/10th the frequency), but below that the difference becomes apparent. There may be as much as 20dB more level applied to the tweeter at 20Hz with a series crossover vs. an otherwise identical parallel version (with an inductor DCR of 0.8Ω). Note that because the inductor for the series network has half the inductance, it follows that it will (or should) have half the resistance as well. This negates the difference seen if the inductor resistance is maintained at 800mΩ (as used in the simulations).
* Although there is a small loss of level, the parallel crossover's theoretical response is greatly disturbed by even a 0.8 DCR in the inductor. This will cause a response anomaly of about 1dB, with the woofer output being 0.8dB down at one decade below crossover frequency. Naturally, higher resistance will create more deviation in response. The series network's overall response is similarly affected, but to a slightly lesser extent. Normally, the inductor's DCR must be factored into the design, regardless of crossover type.
Because of the reduced tweeter attenuation at low frequencies and the sensitivity of any second order filter to DC resistance in the inductor, it's hard to recommend a 12dB/octave series crossover. The parallel version has the same performance, but is slightly less sensitive to DCR and small component variances. When properly aligned, the two are essentially identical, but the parallel crossover is a better choice overall. It uses smaller capacitors, and there is no possibility of interaction between the filters if the amplifier has a high damping factor (greater than 20 is recommended).
As was shown to be the case with the first order implementation, by its very nature, the two segments of a parallel crossover are separate, and share only the amplifier's output impedance, plus the impedance (R, L and C) of the speaker lead. Speaker lead capacitance may safely be ignored as it is insignificant compared to the capacitances within the crossover network.
A series network on the other hand, relies on the integrity of the series elements - all of them. A change in woofer parameters (for example) therefore affects the tweeter, and vice versa. The tweeter is likely to have smaller and fewer changes than the woofer in a practical system.
It is interesting to see the behaviour of the two network types when the outputs are summed electrically. This is a severe test, and in 12dB types, neither crossover is significantly worse than the other in this respect.
Any change in the parameters of the woofer (the most likely to change) causes a change in the tweeter parameters, and the summed electrical response varies with both types. Since it has been established that the two filter types are identical when all values are at their design figures, there is no point showing this. The following two charts show the extremes - with the woofer impedance at 4 ohms and 12 ohms (the latter value being much more likely).

Figure 2.2 - Series and Parallel - Woofer at 4Ω
The red trace is the summed electrical response of the parallel network, and green for series. The dark green and violet traces (with the kinks and bends) are the individual responses for the series network.
Note that although both series and parallel networks have deviated from the ideal, the parallel network has a flatter and less rapid change. Overall, the difference is marginal.

Figure 2.3 - Series and Parallel - Woofer at 12Ω
Here, we see the change when the woofer impedance is increased to 12 ohms. The series network is slightly better, but there is very little between the two. The rise at crossover frequency has changed from 3dB (normal) to 4.9dB - this will be audible in both cases.
The impedance 'seen' by the drivers is also important. This may be referred to as 'look-back impedance'. The woofer is expected to be effectively short-circuited by the amplifier at low frequencies, and both networks achieve this quite well. Interestingly, the parallel network loses control at the crossover frequency. This is shown in the following diagram. The loss of control at this frequency is relatively unimportant if the cabinet is well damped, but may cause colouration with some systems.
In the following graph, each trace indicates the current generated when a 1V source is connected in series with the woofer. This represents the back EMF generated by the cone's momentum when the signal changes. The red trace shows the current in the parallel network, and as can be seen, it drops to a low value (high impedance) at the crossover frequency. A series network maintains relatively good control over this region, tapering off (impedance increasing) gradually.

Figure 2.4 - Series and Parallel - Woofer Back EMF Current
The next test is to see how well each network maintains separation of the signal generated by the woofer. It is important that woofer back EMF (in particular) is not seen by the tweeter, as this may create intermodulation. The 2nd order network is the same as a 1st order network in this respect, except that the slope is 12dB/octave as is expected of a second order network.

Figure 2.5 - Series, Woofer Back EMF Rejection
The amount of this signal reaching the tweeter should be zero (or close to it). The parallel network is not shown, since it is at zero. Not so good for the series network however, with more than half the generator voltage appearing at the tweeter terminals at the crossover frequency. Even at 300 Hz, the voltage is significant at 100 mV (20dB down from the full 1V applied). As with the series 1st order network, the back EMF rejection is 3dB better than the attenuation of the amplifier signal below crossover frequency.
The levels shown are not a real concern, since woofer back EMF will always be much lower than the amplifier signal. While it would seem ideal to limit such cross-coupling to the minimum possible, the effects are something of an unknown, and back EMF can be expected to be quite low with typical drivers - especially where the box is well damped internally.
Given that valve amplifiers typically have an output impedance of 6 ohms (when operated without global feedback), the differences between the series and parallel configurations become very similar, with the parallel network being only 2.7dB better than its series counterpart.
The differences between second order series and parallel filters are more difficult to rationalise. Each has strengths and weaknesses, but from the above, the parallel version probably has a slight advantage. Both exhibit variations in response when the woofer (or tweeter) characteristics change, and they are quite similar. The parallel filter has better woofer back EMF rejection in the tweeter circuit, while the series crossover has a better woofer 'look back' impedance characteristic.
Components for a series crossover will be more costly because of higher capacitor values, but it will have lower losses due to inductor resistance, since they are lower values. For those who feel that capacitors change the sound, the higher values may be thought to have a greater effect
It is very difficult to make any judgement of series or parallel crossovers as a generalisation. The series first order network is probably a better choice in general, due to its flat response regardless of driver impedance - this can simplify the design, but at the expense of having the crossover frequency shift from the design value.
The choice is more difficult for the second order crossover, since both series and parallel have vices and virtues, with neither standing out as generally superior. Overall, the parallel version is probably a better choice, if only because it is slightly more tolerant of variations, and will probably have marginally lower losses because there is no series connection of the drivers (this adds the resistive losses in the inductors, whereas they are in parallel in the parallel filter - of course).
As for any claims for better transient response or sound quality, this is very doubtful - there is nothing to suggest that either version if properly designed will outperform the other to any degree. Parallel crossovers are easier to design, and are simple to convert to a (sub) Bessel response with a Q of 0.5 (approximating a Linkwitz-Riley response).
Most constructors who have attempted second order series crossovers have had to spend considerable time tweaking to get it right - they are harder to design than their parallel counterpart, and interactions will always cause problems.
As a final examination, Figure 3.1 shows a series and parallel network, using simulated drivers. There is no compensation applied for woofer inductance or tweeter resonance, yet both effects are present.
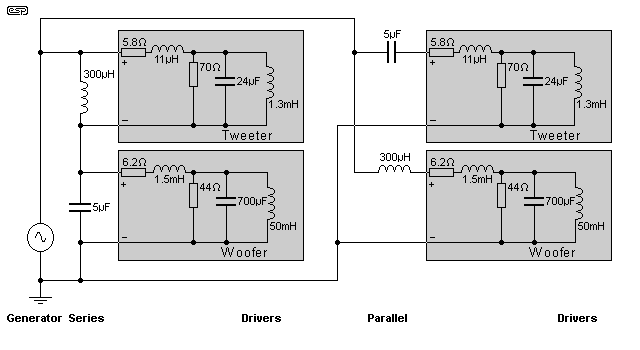
Figure 3.1 - Series & Parallel, With Simulated Drivers
The grey boxes are the drivers (identical in each version), and the area outside the boxes contains the generator and filter networks. As you can see, these are the same in each case, with the values deviating from the previous simulations only in that this design is for a real crossover network (a very similar design is used in my PC speakers, as described in the ESP projects section - see Project 73). The values are slightly different from those shown, but the principle is identical!
A transient analysis shows the following outputs, using a nominal 4kHz crossover frequency (as per the circuits above) and an input signal of 1kHz ...

Figure 3.2 - Transient Response, 1kHz Squarewave Signal
The series crossover output is shown in red, and the green trace is the parallel network's output. This is electrical summing, but it shows clearly that the driver characteristics are fully compensated by the series network, and the output is exactly the same as the input. The parallel network by comparison indicates severe waveform distortion, and this implies phase and levels are incorrect - remember that no attempt was made to optimise the driver impedance with Zobel or notch filters in either case. Note that the parallel crossover takes a few cycles before 'steady-state' conditions are reached. This is completely normal, and applies with most filter networks.
This is fine in theory, so to prove the point one way or another, the following are real impedance and response plots from two identical (inasmuch is possible) boxes, measured under identical conditions, and within a few minutes of each other. The boxes are my PC speakers, as described above, using shielded Peerless tweeters, and small (unbranded) polypropylene woofer drivers.

Figure 3.3 - Impedance Comparison, Series vs. Parallel
The measured impedance differences are as likely to be the result of slightly mismatched drivers as anything else. There is not a great difference at all. The red trace is the series connection, and black is parallel.
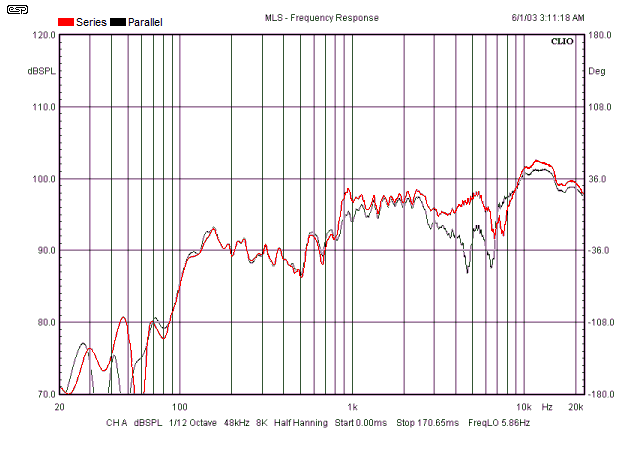
Figure 3.4 - Frequency Response Comparison, Series vs. Parallel
Response differences are a bit more pronounced (again, red is serial and black is parallel), but are not as we should expect based on the simulations. Simulation showed perfectly flat response, but remember that was an electrical signal only, and fails to account for driver behaviour. Note that there is a noticeable improvement at the crossover frequency of 4kHz - the series network is flatter, indicating that the theory does work (the drivers have no impedance compensation - these are PC speakers, and make no claim to be being hi-fi).
Finally, after converting the second enclosure's crossover to series, I did another response comparison. As you can see, there are still differences between boxes, with one tweeter being more efficient than the other. This alone would account for some of the differences seen in the series-parallel comparison.

Figure 3.5 - Frequency Response Comparison, Series, Left vs. Right
The glitch at 7kHz appears to be caused by a diffraction, probably from the woofer's surround (which projects slightly from the frame, and is at the correct distance for that frequency). As for sound differences between the series and parallel connections, there was very little that I could hear. The microphone is much more sensitive to small variations than the ear, and there are quite dramatic variations in response as one moves around - far greater than the differences measured between the series and parallel connections. This shows up readily if one moves the measurement mic even a small distance, and the fact that the two sets of response graphs look quite different is evidence of this. The mic was moved about 50mm further away from the speakers for the second chart.
Spectral decay plots were also done, but are not shown - there are marginal differences as one would expect from the frequency response variations, but little else.
So, although a simulation shows that a first order series crossover is superior to its parallel equivalent, the fact is that the differences are slight. The evidence was sufficiently compelling for me to change the crossovers in my PC speakers, but the huge difference in sound quality one might expect was not forthcoming. More revealing drivers may well sound better to a critical listener, but the differences are hardly 'chalk and cheese' as some may imply.
Despite the differences that have been shown, the loudspeaker drivers should always be carefully equalised with Zobel networks and/or series resonant networks to equalise impedance peaks. This is essential to achieve a flat impedance and allow the crossover to function properly. Once the impedance is flat, it is resistive, and as has been shown above, the two networks are virtually identical with resistive loads. Therefore, it follows that a properly executed Zobel (and a notch filter for the tweeter resonance) will cause real-world series and parallel crossover networks to behave in an identical manner, with the (relatively) small difference of woofer back EMF applied to the tweeter.
The phase and transient response of both filters will match exactly with impedance equalisation, so in a properly designed crossover network, there is nothing to choose between the two. Certainly, the parallel variant is easier to design, and this alone is probably a good reason to stay with a parallel crossover - and probably also explains why the vast majority of loudspeaker designers use parallel rather than series filters in commercial products. In addition, a series crossover cannot be biamped or biwired (assuming that you consider this important).
It is safe to say that neither crossover is possessed of any magic (only skill), so be very wary of any claims that a particular crossover topology is "vastly superior" or "infinitely more transparent" (or any other hyperbole that may be thrust upon you) in advertising material. All crossovers, and indeed, all loudspeakers, are a compromise. The topology of the crossover is relatively unimportant, but the skill and patience required to execute it properly is what really counts. In particular, great attention needs to be paid to impedance compensation for both the woofer and tweeter to prevent unwanted interactions, and the tweeter's attenuator needs to be carefully worked out to get the levels right.
Needless to say, an active crossover has no equal, and it will be vastly superior to any passive network in any system. There is (effectively) infinite attenuation of driver back-EMF when each loudspeaker driver has its own amplifier, but of course tweeters must always be protected from DC or other low-frequency energy from the amplifier, because the tweeter is often connected directly to its power amp (a suitable series cap is a good idea to protect the tweeter from damage).
 Main Index
Main Index
 Articles Index
Articles Index