

|
| Elliott Sound Products | Capacitance Multipliers |
 Main Index
Main Index
 Articles Index
Articles Index
In the Project 15 page, I have described a number of different approaches to a capacitance multiplier. While this is a useful resource, it doesn't delve into the design criteria, so this article is intended to provide you with enough information to design your own. There is also an article in the 'TCAAS' section of my site (see JLH Capacitance Multiplier), but this doesn't cover the design criteria in much detail either. The original John Linsley-Hood version (see Simple Class A Amplifier, page 9) uses a single-pole filter, which is nowhere near as good as the version described here.
The article Linear Power Supply Design should be considered essential reading before embarking on a capacitance multiplier, as many of the essential elements are discussed in detail. Parts 2 and 3 are also interesting, but don't cover high current supplies.
While a capacitance multiplier is superficially simple, there's actually more to it than you might think. Everyone who uses this type of circuit calls it a 'capacitance multiplier', and while you may think it's also a crude gyrator (simulated inductor), this isn't the case. The behaviour is similar to a very much larger capacitance, but there are some significant differences.
A 'capacitance multiplier' is really just a buffered filter, with the filter response set by the resistance and capacitance at the base circuit. Capacitance is not multiplied by the gain of the transistor(s), only the current flowing through the base resistor. However, there's more to it than that. In particular, there's a great deal to be gained by using two capacitors, separated by a second resistor. This improves ripple rejection because the filter is converted from first-order (6dB/ octave) to second-order (12dB/ octave).
Despite the name 'capacitance multiplier' being a misnomer because nothing of the sort happens, I'll still use the term in this article. Calling it a 'buffered passive filter' is more accurate, but doesn't convey the same idea, as the original term has been used for years and it's something that people are used to. Provided you understand that the original term is inaccurate (or just plain wrong) and understand how it works, it doesn't matter what it's called.
A simple passive filter can't be used with significant current because the voltage drop across the resistors would be prohibitive unless they are very low values (less than 1Ω). This is impractical, because the capacitance needed to obtain a -3dB frequency of less than 1Hz becomes very large. For example, a filter using 1k and 1,000µF has a -3dB frequency of 159mHz. If the resistor is reduced to 1Ω, the capacitance would have to be 1F (that's 1 Farad!). Using a transistor emitter-follower means that we can use higher resistance and lower capacitance, with the transistor providing the current, rather than directly from the filter.
A single transistor doesn't have enough gain to allow the use of comparatively high resistance. The TIP35/36 devices I suggest will have a 'typical' gain (hFE) of around 45, and around 100 for the BD139/140. This gives a total theoretical hFE of 4,500 but it will be less than this in reality. A value of 1,000 is a realistic figure to work with. This means that resistors can be (up to) 1,000 times the value needed for a passive filter, and the capacitance will be 1/1,000th of the value otherwise needed. Because we will adopt a 2nd order filter (12dB/ octave) it's possible to reduce the capacitance further than would be the case with a single resistor and capacitor, with no loss of performance. Indeed, the reverse is true, with faster response and better filtering.
While it would seem to be ideal, a MOSFET isn't recommended for a number of reasons. Section 6 explains the reasons for not using a MOSFET. Because they have very high input impedance, low values of capacitance and correspondingly high resistor values can be used, but the issues are with the MOSFET itself.
Note that in this article, I have avoided extensive mathematical analysis. A published article [ 2 ] that I saw went in the opposite direction (all maths, with little or no practical application) which made it pretty much useless for hobbyist constructors. The engineering is all quite correct, but the application was ... unhelpful (IMO). As seems to be typical, the only filter discussed is first-order, so performance was comparatively poor - despite the extensive maths offered.
While having all the equations to hand may seem like a good idea, mostly you don't need them. A few simple calculations are shown here, and you usually don't need anything else. You need to know how to specify the transformer and main filter cap, decide on the transistors you'll use, and do a rough calculation to determine the filter frequency (it should be less than 1Hz if you expect low ripple). These are all mostly straightforward, but transformer selection is more difficult.
In addition to capacitance multipliers, there are a couple of other techniques shown here. These are provided because they are interesting, but they are not particularly useful for most hobbyists because they show solutions that are better achieved using other techniques such as a 'proper' regulator. However, regulators themselves generate noise, but it's generally low enough that it doesn't cause any problems with most circuits. Regulators are not covered here, because they are explained in detail in the articles Voltage & Current Regulators And How To Use Them, Discrete Voltage Regulators and Low Dropout (LDO) Regulators.
For the sake of the exercise, assume that we want the following specifications:
Output Voltage - 25 Volts (nominal)
Output Current - 2.5 Amps max. (1.25 Amps average)
Mains Voltage - As used in your country
These specifications are typical. Australia, Britain and Europe use nominal 230V mains, with (again nominal) 120V used in the US and Canada. However, the mains voltage is immaterial, and only the secondary voltage is important. The mains voltage is subject to variations, both long and short term. The energy suppliers generally claim ±10%, but it can be more in some circumstances. Australia and the UK used to be 240V, and in many cases that's still what is supplied. The US and Canada used to claim anything from 110V to 120V, with 115V often quoted. Europe used to be 220V, and has now changed to 230V, but as with everywhere else, only the claimed nominal voltage was changed, but in most cases no physical changes were made to the network. All circuitry has to assume 'worst-case' variations, and using the claimed voltage alone will always have a significant error.
We are not all that interested in the mains input voltage, only the possible variations at the output of the transformer/ rectifier/ filter combination. While the two are related, the secondary voltage is also subject to copper losses in the transformer (winding resistance). This is particularly troublesome when continuous high current is expected. If the transformer is operated above its nominal VA rating, it will overheat and may be damaged if the overload lasts for too long.
For a nominal output of 25 Volts (for example), we need a minimum input DC voltage of about 28 Volts, since there will be ripple on the DC voltage (See Fig 1.1). This 'minimum' voltage is the instantaneous minimum, including ripple and the voltage drop caused by the transformer's regulation. Note that for all calculations I am assuming 50Hz mains supply. The results will be slightly different for 60Hz, but the difference is not particularly significant. Capacitor values can be reduced by about 15% to account for 60Hz.
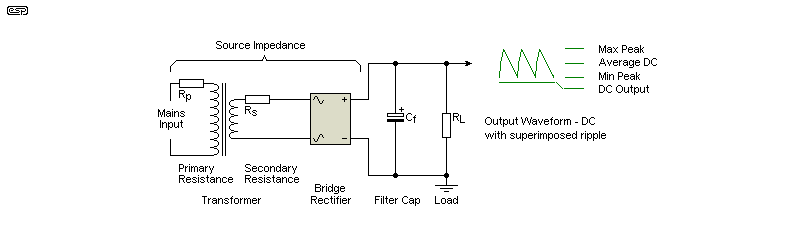
Figure 1.1 - Basic Rectifier, Filter & Load
Your multimeter will show the average voltage, but that's not useful because of the superimposed ripple. Once the amplifier's output voltage increases beyond the 'DC Output' voltage (just below the minimum voltage shown), ripple will appear at the amp's output. This will find its way to our ears as it is the onset of clipping. The combination of Cf and Rsource will always have a -3dB frequency, as it's a simple low-pass filter. Unfortunately, Rsource is not an easy parameter to measure because it's a mixture of mains, transformer and rectifier impedances, complicated by transformer ratios and the dynamic resistance of the diodes in the bridge rectifier.
The only thing we can control easily is the capacitor value. If we use the example above, the DC output voltage is 20V, and the required capacitance is (roughly) determined with a simple formula ...
C = ( I L / ΔV) × k × 1,000 µF ... whereI L = Load current
ΔV = peak-peak ripple voltage
k = 6 for 120Hz or 7 for 100Hz ripple frequency
To obtain (say) 1V of ripple with 1.25A average current, the capacitance needs to be 8.75mF (i.e. 8,750µF) for 50Hz, or 7.5mF for 60Hz. Note that the DC voltage is (almost) immaterial, and 1V P-P ripple (±10%) will be present with a 1.25A load current at almost any voltage you care to use. I've run a simulation showing that with an AC input of 20V, 30V and 40V (peak), the ripple voltage only changes by 20mV (RMS) or about 80mV peak-peak. Perhaps surprisingly, if the power transformer is larger (higher VA rating, so lower internal resistance), the ripple voltage will be slightly greater than you'd get with a smaller transformer. This is almost certainly the opposite of what you'd expect.
When you are drawing a continuous (and relatively high) output current, the DC voltage will be much lower than expected. We nearly always assume that the DC voltage is 1.414 times the AC (RMS) voltage, and at light loading that is true. The transformer's regulation complicates matters, because it's reduced due to resistance in the primary and secondary windings. The manufacturer's regulation figure (if quoted) is based on a resistive load, and a capacitor input filter is anything but resistive.
Determining the transformer VA rating isn't hard either. Using the values from above, we need a 25V secondary (not 18V as you may have thought), and we'll have an average current of 1.25A DC. The AC (RMS) current in the transformer's secondary is roughly double the DC current (it's often taken as 1.8 for a bridge rectifier, but that leaves no margin for error), so 2.5A. The transformer needs a rating of 62.5 VA as a minimum ...
I sec = I DC × 2
I sec = 1.25 × 2
VA = V × I = 25 × 2.5 = 62.5 VA
Note that this is the absolute minimum, and you'll get better regulation (and better performance overall) if you use a bigger transformer. Running a transformer at its full rating for long periods will cause it to run hot, and small transformers always have worse regulation than larger ones. Some people will recommend that the transformer VA rating (for Class-A amplifiers) should be up to five times the total output power. While that might seem like total overkill, it's probably about right. That means you'd use a 200 VA transformer for a dual 20W Class-A amplifier. Because of better regulation, you can almost certainly use a lower voltage (say 20V rated AC output instead of 25V)
If you intend to draw more current or operate with a higher voltage, you can work out the transformer to suit. One of the things that's quite difficult to know in advance is the transformer's regulation. While it will usually be provided in the datasheet, that's for a resistive load, and it's always much worse with a rectifier and capacitor filter. Unless you know the winding resistance for primary and secondary, it can't easily be calculated. For continuous current, as a first approximation assume that the DC voltage will be the same as the rated AC secondary voltage. The DC voltage will always be higher with no-load or light loading. Capacitance multipliers are best used with circuits that draw fairly constant current, and they don't work so well with dynamic (always changing) load current.
One of the nice things about a capacitance multiplier is that you don't need to change much to use it with a higher or lower voltage. The voltage rating of capacitors needs to be high enough of course, but the value shouldn't need to be changed. If the expected current is a great deal more (or less) than the examples shown here, you may need to adjust resistor values, but mostly you won't need to change anything. If you need higher current, suitable transistors should be used, but the dissipated power remains fairly low.
The only real thing to worry about is the degree of filtering needed! We must assume that up to 2 volts may be lost across the capacitance-multiplier filter, to ensure that the DC input (including ripple component) always exceeds the output voltage by at least 2V. Transient performance may also need to be considered if the load current is not continuous. In general, the minimum differential voltage from input to output should not be less than 1 volt (based on the lowest point of the input ripple).
Because there is no regulation, the power amplifier must be capable of accepting the voltage variations from the mains - every standard power amplifier in existence does this quite happily now, so it is clearly not a problem. Note that the output power is affected, but this happens with all amps, and cannot be avoided because the output voltage is a little lower than for a basic capacitor filter.
We can now design for the nominal transformer secondary voltage, and with very simple circuitry, provide a filter which will dissipate no more than about 4 Watts in normal use - regardless of the mains voltage. Figure 3.1 shows the basic configuration of a capacitance multiplier filter, where the frequency response of the filter is in control of the output DC via the emitter-follower connection of the series-pass transistors. This allows a comparatively high impedance filter to be buffered by the output stage, and allows the use of small capacitors rather than very large ones.
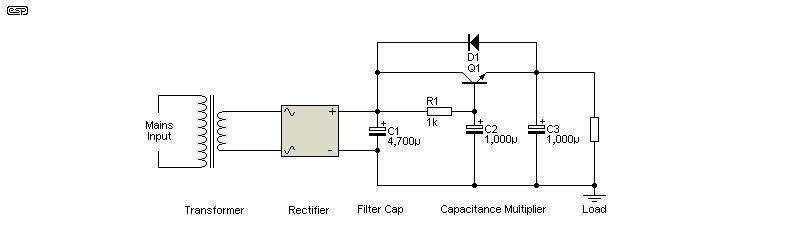
Figure 2.1 - Single (Basic) Capacitance Multiplier
A basic cap multiplier is shown above. The filter is single-pole, and has a rolloff of 6dB/ octave above the -3dB frequency (0.159Hz). This heavily filtered voltage is then buffered by Q1, which is an emitter-follower. D1 prevents transistor damage if a voltage is present at the output but not at the input. This diode is (or should be) used with any regulator or cap multiplier unless there is zero possibility of a reverse voltage being applied. This can happen easily if you use a particularly large output capacitance, but it's never a problem if the diode is included.
Both a 1F (one Farad) filter capacitor and a basic cap multiplier will provide a ripple of well under 10mV RMS at around 3A, but the multiplier has the advantage of removing the triangular waveform - it's not a sinewave, but it has a much lower harmonic content than would be the case even with a 1F capacitor.
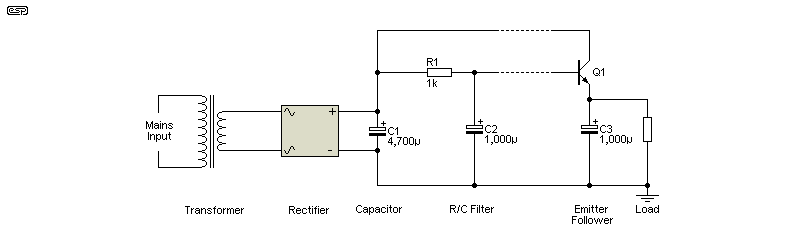
Figure 2.2 - R/C Filter, Emitter Follower & Load
The basics of operation are split into the sections above (D1 has been omitted in this circuit). R1 and C2 form a simple low-pass filter, and it's obvious that if the load were connected across C2, the available current is very low because of R1. The maximum output current without Q1 is limited to about 2mA for a loss of 2V. This is overcome by adding the transistor, which is an emitter-follower used to boost the low current through R1 to drive the load. R1 only has to provide base current for the emitter-follower transistor. Provided Q1 has high gain, very little voltage is 'lost' across R1. However, there has to be some loss which is 'just right' or ripple at the collector will get through Q1 and to the load. Refer to Figure 4.3 to see the voltage relationships.
The simple capacitance multiplier filter in Figure 2.1 is quite satisfactory as a starting point, but its operating characteristics are too dependent on the gain of the output transistor(s). What is needed is a circuit whose performance is determined by resistors and capacitors, and which is relatively independent of active devices (although these will still have some impact on the degree of filtering provided). The Figure 2.3 circuit accomplishes this by using a Darlington pair, which has much higher gain than a single transistor. The gain is important, because with too little gain, R1 (Fig 2.2) or R1 + R2 (Fig. 2.3) need to be a lower value to minimise the voltage drop of the filter network when supplying base current to Q1.
We need to keep the impedance of the filter fairly high (to minimise the capacitance needed), so that requires an output transistor hFE of at least 1,000, so 1mA of input (base) current becomes 1A of output (emitter) current. To obtain a gain of 1,000 for a power transistor, we need to use a Darlington - either an encapsulated Darlington device, or a pair of 'ordinary' transistors connected in a Darlington pair (See Fig. 2.3). The latter is my preferred option, since it allows greater flexibility selecting suitable devices and it will usually have better performance. Another alternative is to use a complementary feedback (Sziklai) pair, as shown in Figure 3.2.
The way it works is fairly straightforward. The degree of hum filtering (for the simple version) is determined by the filter comprising R1 and C2. With 1k and 1,000µF, it's a low pass filter, rolling off at 6dB/ octave from 0.159Hz (-3dB). That means that by the time you reach 100Hz (or 120Hz) the 100Hz ripple is (at least in theory) attenuated by at 56dB, so (for example) 1V RMS of ripple is reduced to 1.6mV (RMS). This is far greater than you can achieve with a capacitor alone. The next phase is to add another filter as shown in Figure 2.3, so the rolloff is increased to 12dB/ octave. With 2 x 500Ω resistors and 2 x 500µF caps, the output ripple is reduced to about 40µV (almost 90dB). Of course, this is all well and good (again in theory), but the transistor itself will prevent you from achieving this. However, a ripple attenuation of 60dB is easily achieved.
The final step is to add a resistor to ensure that the output voltage is just below the most negative part of the ripple waveform. In the designs shown below this has been included. If it's left out, the output ripple is over 30 times greater. Many designers have failed to perform this analysis carefully, and the final resistor is omitted. R3 makes almost no difference to the DC output (it's reduced by around 200 millivolts), but that tiny bit of 'headroom' makes a big difference to the ripple appearing at the output.
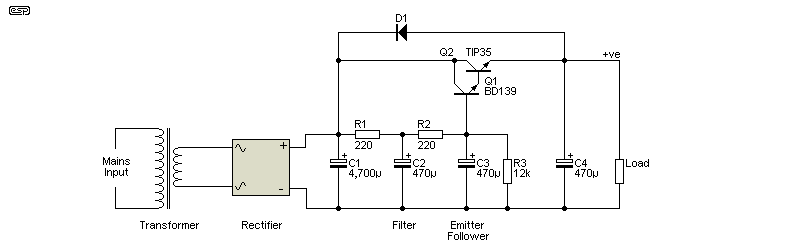
Figure 2.3 - Single (Final) Capacitance Multiplier
A complete design (single polarity) capacitance multiplier is shown above. Dynamic loads are less than ideal with a capacitance multiplier, but it can be done, and more details are shown below. The 2-pole filter is far and away the better configuration, and it is (more-or-less) suitable for dynamic loads. It's not perfect (nothing is), but the voltage recovery can be made fast enough to get good performance. Increasing the speed means less ripple reduction though, so it's always a compromise.
When a 2-pole (12dB/ octave) filter is created using a passive design, the -3dB frequency is increased by a factor of about 1.56. For example. a single-pole filter with 1k and 1,000µF cap has a -3dB frequency of 159mHz, but when that's split into 2 x 500Ω resistors and 2 x 500µF caps, the -3dB frequency is 248mHz. At 100Hz, the 6dB filter is -56dB down, but the 12dB filter is nearly 74dB down, a significant improvement! With the values used in these examples, the hum is just under 73dB down at 100Hz, reducing the ripple by a factor of more than 4,700. Feel free to increase the value of C2 and C3 if you wish, but you probably won't hear the difference. The resistance of R1 and R2 has been reduced to 220Ω to ensure that there's always enough base current for Q1.
The output capacitor (C4) is only needed to provide a small amount of transient current and to ensure that the connected amplifier remains stable. Although I've shown 470µF, it can be increased or reduced if you wish. It makes little difference to the filtering, because the output impedance of the emitter-follower series-pass transistor is very low. At 100Hz, the impedance (capacitive reactance) of a 470µF capacitor is 3.4Ω. The final output impedance from the emitter-follower will be a few milliohms, and C4 doesn't change that. A larger value will help to provide transient current, but it's unlikely to make any audible difference. The transistor's gain will fall at high frequencies, so the output capacitor maintains a low output impedance up to several hundred kHz. Feel free to add a film capacitor in parallel with C4, but don't expect it to have any measurable or audible effect.
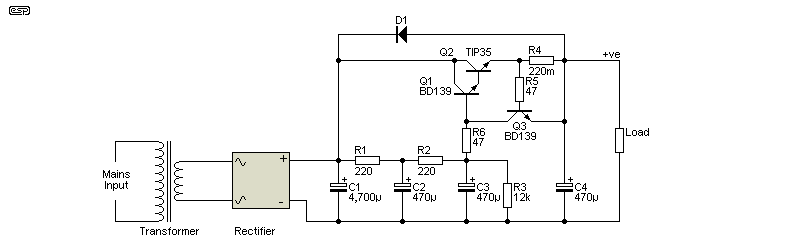
Figure 2.4 - Single Multiplier With Current Limiter
Like regulators, capacitance multipliers are utterly intolerant of an output short-circuit. If the output is shorted, Q1 and/ or Q2 will fail almost instantly, and there is no 'safe' short-circuit duration. Adding very basic current limiting as shown above will (hopefully) provide some protection, but it's limited to very brief 'events' and it cannot tolerate a long-term short. The output current limit is set by R4, and Q3 will conduct if the voltage exceeds ~3A. A higher value for R4 means lower current and vice versa.
This can be applied to any of the circuits shown, but it will generally be an unnecessary complication. You do need to be aware that without protection, a shorted output will cause the demise of Q1 and Q2. There's a remote possibility that a fuse will provide some protection, especially if C4 is a larger value than shown. It's doubtful though, because fuses are generally not fast enough to protect transistors. A chap I used to work with (many, many years ago) called transistors '3-legged fuses' and the term is just as applicable today as it was then.
The final circuit for a dual supply is shown in Figure 3.1. This circuit reduces ripple to less than 1mV with typical devices (about 250µV RMS as simulated), and dissipates less than 4 Watts per output transistor at 1.25A continuous operating current. It is unlikely that you will achieve this low hum level in practice, since real wire has resistance and capacitor ESR also has an influence. However, with careful layout you should easily be able to keep the output hum and noise to less than 5mV, and this level is usually more than acceptable for a power amp.
As noted above, by splitting the capacitance and adding another resistor, we create a second-order filter (12dB/octave rolloff), which reduces the hum more effectively, and also removes more of the higher order harmonics (which tend to make a 'hum' into a 'buzz' - much more audible and objectionable). The resistor to ground (R3) stabilises the circuit against variations in transistor gain, but increases dissipation slightly. This is done deliberately to ensure that there is sufficient voltage across the multiplier to allow for short term variations.
The 12k resistor shown may need to be adjusted to suit your transistors and supply voltage. Reducing the value increases dissipation in the output devices and lowers output voltage. It is unlikely that any benefit will be obtained by increasing this resistor, but you may experience increased hum (hardly a benefit).

Figure 3.1 - Complete Dual Capacitance Multiplier (Darlington Pair)
This is an easy design to build, but requires great care to ensure that ripple currents are not superimposed on the output because of bad grounding or power wiring practices. The schematic is drawn to show how the grounds of the various components should be interconnected, using a 'star' topology. If this is not followed, then excessive hum will be the result. The grounding area needs to be big enough to provide space for all the connections, but not so big that there can be any circulating currents. All capacitor leads must be as short as possible. Wire has both resistance and inductance, and these can combine to provide significant performance degradation.
Normally, a schematic diagram is intended to show the electrical connections, rather than the physical circuit layout. This diagram is an exception, and the physical layout should match the schematic (inasmuch as that is possible, at least). Surprisingly little resistance is needed across a high current connection to produce a measurable performance degradation.
Note that the transformer is centre-tapped, and requires equal voltage on each side - selected to give the voltage you require. It is most important that the centre-tap is connected to the common of the two input filter capacitors (4,700µF), and that this common connection is as short as possible. Use of a solid copper bar to join the caps is recommended. Likewise, a solid copper disk (or square) is suggested for the common ground, tied as closely as possible to the capacitor centre tap. The resistance of the main earth connection is critical to ensure minimum hum at the output, and it cannot be too low.
Because the circuit is so simple, a printed circuit board is not needed, and all components can be connected with simple point-to-point wiring. Keep all leads as short as possible, without compromising the star grounding. For convenience, the driver transistors may be mounted on the heatsink, which does not need to be massive - a heatsink with a thermal resistance of about 5°C per Watt (or better) should be quite adequate (one for each output device). Remember that the lower the thermal resistance, the cooler everything will run, and this improves reliability.
Increasing the capacitance (especially at the input) is recommended, and I would suggest 4,700µF as the absolute minimum. More capacitance will reduce hum even further, and provide greater stability against short term mains voltage changes. Increased output capacitance C4) will help when powering Class-AB amplifiers to account for their sudden current demands. I do not recommend more than 4,700µF for C4, as the charging current will be very high and may overload the series pass transistors.
Although generic transistor types (such as the 2N3055) can be used, it is better if devices with somewhat more stable characteristics (from one device to the next) are used. Plastic (e.g. TO-218) devices are fine for the output as shown, but if higher voltage or current is needed you might have to use TO-3, TO-3P, TO-264 (etc.) types. While you might get away with using TO-220 packaged transistors, be aware that they have poor thermal properties, and getting heat from the case to the heatsink is always a challenge.
For the components, I would suggest the following as a starting point (or equivalents):
Output Transistors TIP35 (TIP36 for the -ve supply) Drivers BD139 (BD140 for the -ve supply) Resistors ½W metal film for all resistors Diodes 1N4001 or similar Electros No suggestions, but make sure that their operating voltage will not be exceeded, and observe polarity.
(Bypassing with polyester is not necessary, but if it makes you feel better, do it)Bridge rectifier 20 to 35A Amp bridge is recommended. This is overkill, but peak currents are high, especially
with large value capacitors. Also ensures minimum diode losses at normal currents.Transformer Ideally, use a toroidal. Power (VA) rating for supply should be 'as required' for the amplifier.
A dual 20W Class-A amp will have a preferred transformer rating of 200 VA - 5 times the amplifier power.
(Note that VA is sometimes incorrectly quoted in watts). Primary voltage is naturally dependent upon where you live.
Matching the output and driver transistors is not necessary and will not affect performance to any degree that's audible. Use devices with the highest gain (hFE) possible for best results. Transistor gain must be measured at (or near) the typical operating current or the measured value is not useful. Most hand-held 'all-purpose' component testers are useless for measuring power transistors, because the test current is far too low to give a usable reading.
To use the above circuit in single-ended mode, the transformer will need only a single winding (or paralleled windings). Simply wire the whole circuit as shown in Figure 2.3. See further below for a complete dual single-polarity version. A complementary version of the Figure 3.1 circuit is shown next.
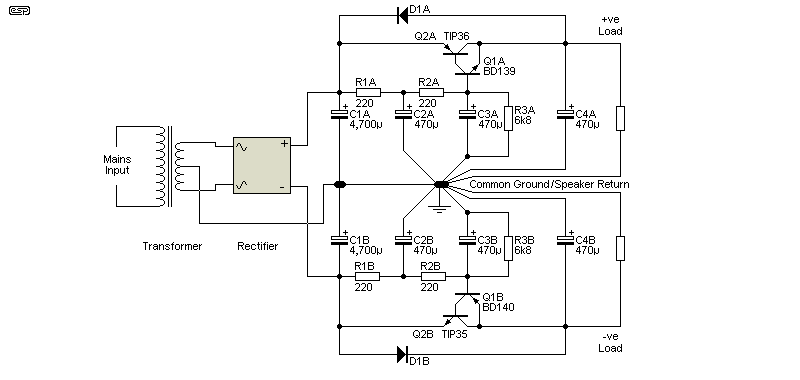
Figure 3.2 - Complete Dual Capacitance Multiplier (Sziklai Pair)
The voltage drop across the series pass transistor can be reduced if a complementary (aka Sziklai) pair is used rather than the Darlington connection shown. For the positive supply, the driver may be a BD139 (NPN), but the output device would be TIP36 or TIP2955 (PNP). This arrangement has almost the same gain as a Darlington pair, but the lower forward voltage may be considered an advantage as overall dissipation is slightly lower.
However (there's always a 'however'  ), as unlikely as it may seem, the performance of the Sziklai pair is worse than the Darlington unless the value of R3 is reduced. With it set at 6.8k, the performance of both circuits is virtually identical, and there's nothing to be gained. It's usually easier to wire a Darlington than a Sziklai pair, so the Darlington connection is the 'winner' in this comparison.
), as unlikely as it may seem, the performance of the Sziklai pair is worse than the Darlington unless the value of R3 is reduced. With it set at 6.8k, the performance of both circuits is virtually identical, and there's nothing to be gained. It's usually easier to wire a Darlington than a Sziklai pair, so the Darlington connection is the 'winner' in this comparison.
In all cases, and regardless of the transistor configuration, beware of the charging current into C4. If you use a very large capacitor in that location, the series-pass transistors will be at risk every time you turn on the power. The saving grace (as it were) is that the voltage comes up comparatively slowly as C2 and C3 charge, but if C4 is too large that may not be enough to save the transistors.
It's worthwhile to look at the difference between single-pole (6dB/ octave) and 2-pole (12dB/ octave) filter networks. This is important, as you might think that a single-pole filter should perform better with a constantly varying load. As it turns out, this isn't the case at all, and a 2-pole filter outperforms a single-pole filter in all respects ... including speed!
These circuits are suitable for Class-AB amplifiers, but since their current requirements vary so widely, adding a larger capacitance to the output is a must. The diode should be a high-current type as it may be subjected to more 'abuse' than is normally the case due to the current variations of Class-AB amplifiers. It's highly debatable if there's any real advantage when the load current changes continuously, but it's not difficult to run the simulations, and 'real life' will be almost identical to the simulated results.
When a capacitance multiplier is suddenly loaded, there will be some ripple 'breakthrough', because the voltage across the circuit is reduced when the load current is increased. If the voltage across the series pass transistor falls, there may not be sufficient reserve to maintain the minimum value of ripple voltage. It is very uncommon to find capacitance multipliers used with Class-AB amplifiers, because their supply current is constantly changing and the benefits are dubious. Consider that millions of Class-AB power amps are in use worldwide, and none that I know of use a capacitance multiplier. A few old designs did use a (very basic) regulated supply, primarily because they were single-supply designs with an output capacitor. Supply voltage modulation could cause some infrasonic disturbances, but even then most just used an 'ordinary' power supply.
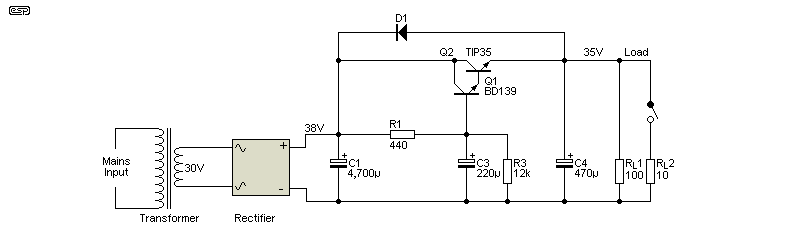
Figure 4.1 - Single-Pole Capacitance Multiplier Test Circuit
Most of the articles (and videos) discussing capacitance multipliers only look at the single-pole version shown above. From the description I've already provided, you know that a single-pole filter is inferior to double-pole (2-pole). While it may come as a surprise, a 2-pole filter also recovers slightly faster when a load is applied or removed with the same overall filter values. I expect that at least some of the apparent reticence may simply be due to a lack of interest.
If the load is variable, a 2-pole filter is still preferable, but ripple rejection has to be sacrificed for a faster recovery time. The only change is that the capacitance is reduced. With the values given in Figure 4.1, ripple reduction is about 4 times worse than the Figure 2.3 multiplier, and the recovery speed of the latter (after a high-current load is removed) is still slightly faster. With a load current varying from 360mA to 2.8A, the single pole filter recovers to 35V in 275ms vs. 193ms for the 2-pole version.
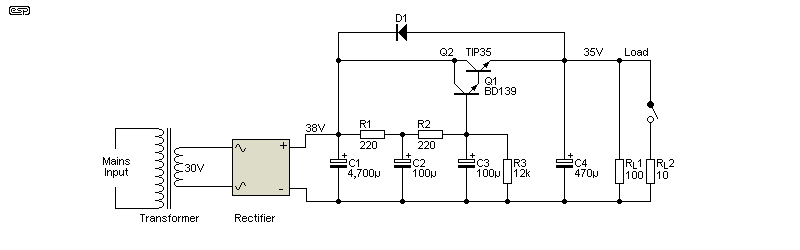
Figure 4.2 - Double-Pole Capacitance Multiplier (High Speed)
There can be no doubt that the 2-pole capacitance multiplier outperforms a single-pole version in every respect. I managed to get that part right when I published the first version back in 1999, but almost every other description fails to mention anything other than single-pole filters. I have no idea why this is the case, especially given the superior performance of a 2-pole filter.
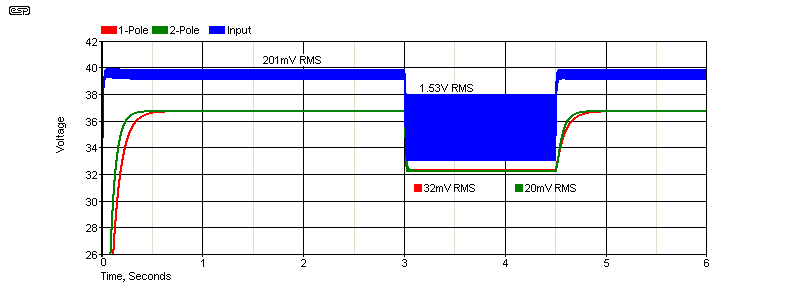
Figure 4.3 - Single-Vs Double Pole Capacitance Multiplier Comparisons Test Circuit
For the above, the simulations were set up as shown in Figures 4.1 and 4.2. All voltages shown are AC-coupled RMS values, so show the ripple voltage present with a 100Ω load for the first 3 seconds, then with an additional 10Ω load switched in. It's turned off again at 4.5 seconds so the recovery time can be seen. Next, I've zoomed into the point where the 10Ω load is turned off, and you can see the recovery for the two filters.

Figure 4.4 - Single-Vs Double Pole Close-Up Response
The input voltage (across C1) recovers very quickly, but the multipliers are much slower. Naturally either circuit can be made faster by using smaller capacitors, but ripple rejection suffers. Of course, you may decide that you don't need very high ripple rejection, in which case the capacitance can be reduced further. With C2 and C3 at 33µF, you still reduce ripple by 24dB (from 1.53V to 94mV RMS, or 4.9V p-p down to 240mV p-p). Recovery is almost instant, taking only 48ms to get back to 36V.
The idea of a multi-pole filter can be extended to a 3-pole version. This will give better ripple attenuation and a faster response, but at the expense of more parts (one extra resistor and capacitor). The law of diminishing returns comes into play though, and it's unlikely that the improvement will prove worthwhile. A 2-pole filter is a good compromise, and it has performance that's 'good enough'. Almost any circuit can be improved, but if the improvement isn't audible then it's rather pointless.
Note that the supply voltage to the power amp(s) will be modulated by the instantaneous current drain of the amp, but this happens with 'conventional' supplies too. For any dynamic load, you have to sacrifice ripple rejection for speed, otherwise the results will almost certainly be unsatisfactory. Even if a 2-pole filter is optimised for speed, it's still slower than the recovery of a supply with only a simple filter capacitor.
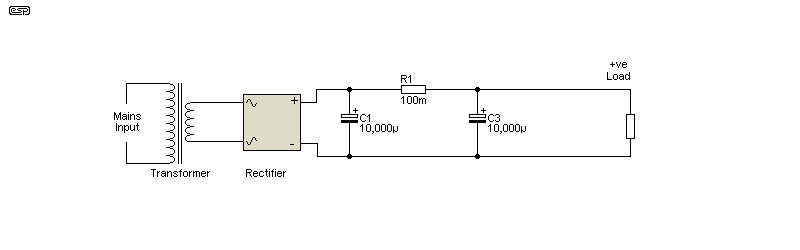
Figure 4.5 - Pi Filter
An alternative arrangement is a 'pi' (π) filter, with two (usually fairly large) capacitors separated with a resistor of perhaps 0.1Ω. Figure 5.5 shows a main filter cap of 10,000µF, a 0.1Ω resistor and a second 10,000µF cap for the π filter. The cap multiplier shown in Figure 4.2 uses only 4,700µF for the filter cap, yet the multiplier wins hands down. This is despite the smaller filter capacitor and far less overall capacitance. There's less ripple - just over 1V p-p for the π filter, and 246mV p-p for the multiplier. Recovery speed is close to identical, but the cap multiplier drops about 2.7V at 3.6A (the test current in the simulation) and the series-pass transistor will dissipate power (around 10W at 3.6A).
Of course you can also use an inductor instead of a resistor, and while more effective, it will be large, heavy and expensive. Increasing the resistor value helps a bit, but the multiplier still has lower ripple. Unfortunately, the multiplier has a greater voltage loss and dissipates more power than a simple π filter. As always, there's a trade-off, and the better solution depends on your requirements.
Overall, the capacitance multiplier will be cheaper and smaller, but the need for a heatsink probably negates any cost saving. There are also active semiconductors in the power supply that will always be at risk if there's a short across the power supply. As always, there are compromises, and it's up to the designer to decide which compromise is the 'least worst'. Mostly, there's a great deal to be said for keeping circuitry as simple as possible, provided overall performance isn't compromised.
If a 'traditional' power supply filter is shorted, it's not very good for the capacitor(s) due to the very high instantaneous current, but it will almost certainly survive (and the mains fuse will blow if it's powered on at the time). Do the same with a capacitance multiplier, and it's almost guaranteed that the series-pass transistors will die instantly. Of course, one could add a current limiter, but then there are even more parts, and a PCB would be essential. These are all design considerations that influence a final circuit, and adding parts that make no audible difference to the sound is something manufacturers (and most hobbyists) avoid.
Project 36 (Death of Zen or DoZ) is a simple Class-A amp that can benefit from using a capacitance multiplier, as can many others. To reduce the stress on the series pass transistor, it's easy (and probably cheaper) to build two capacitance multipliers as shown in Figure 4. Each multiplier is designed to provide the required single supply of 30-35V DC. By using separate cap multipliers we also isolate each amplifier, so they are very close to being mono-blocks, with only the power transformer being shared.

Figure 5.1 - Complete Dual Capacitance Multiplier (Single Supply, Darlington Pair)
This scheme is similar to that shown in Figure 3.1, except that both capacitance multipliers are the same. While the earthing/ grounding arrangement has not been shown diagrammatically this time, it's just as important to ensure that there is a single earth point, and care is needed to ensure that no ripple current can be re-injected into the DC via stray earth resistances.
If used with the DoZ amp at higher than normal quiescent currents, you may need to either reduce the 220Ω resistors to around 150Ω or increase (or even remove) the 12k resistors to get 30-35V DC from a 30V transformer. Dissipation in the TIP36 (or whatever you decide to use) will be around 6-7W with a current of 1.7A, so there's not a great deal of heat to dissipate in the heatsink.
Expect the output ripple to be around 1mV RMS or less with a current of 1.7A, with ripple being lower at reduced output currents. With 4,700µF main filter caps as shown, there will be a fairly high ripple voltage on the raw supply, but the output ripple is reduced by more than 50dB when the capacitance multiplier is used.
While it is certainly possible to reduce the ripple even more, it adds cost to the circuit and the benefits are doubtful at best. With a power supply rejection of better than 50dB itself, DoZ should be noise free into even the most sensitive of horns when powered by a capacitance multiplier power supply.
You can even use a pair of positive capacitance multipliers (this also works with regulators) to get both positive and negative outputs. The circuit is shown below.
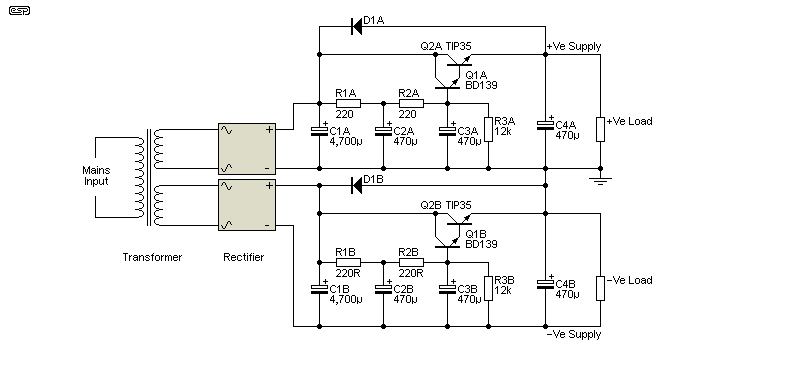
Figure 5.2 - Positive & Negative Outputs From Two Positive Supplies
This can be useful if you don't have any PNP transistors that are suitable, but want to get your circuit working without having to buy more parts. It falls into the category of 'useful to know', even if you don't use it. It's usually easier to build two identical circuits than to make them complementary. The loads don't see the slightest difference - electrically, it's identical to using a complementary circuit for the negative supply.
A MOSFET based capacitance multiplier can work very well, but it's not as straightforward as it may seem at first. In the original Project 15 article I showed a more-or-less suitable design, but it's very hard to recommend because of the greater voltage loss. You'll typically have at least 4.5V across the MOSFET, so power dissipation is a great deal higher than the Darlington configuration. While you should be able to get ripple below 1mV easily enough, the increased power loss makes it far less attractive.
While most implementations I saw still resolutely stick with a first-order (6dB/ octave) filter, a second-order (12dB/ octave) filter still wins for response time and ripple rejection. This is the case regardless of the transistor type used (BJT or MOSFET). Most MOSFETs available now are designed for switching, not linear operation. If you do wish to experiment with a MOSFET version, choose a high-current device with a fairly high RDS-on ('on' resistance), as these are less likely to fail with linear DC operation. Make sure that you check the datasheet, and look at the SOA (safe operating area) for DC operation.
One of the more intractable problems is that the gate draws no current, yet this is apparently a good thing. Because there is no gate current to speak of, transient behaviour as a load is applied is dreadful, with considerable ripple breakthrough. This happens because there is no rapid discharge path for the filter capacitors. When the input voltage falls, the gate remains at a higher than desirable voltage for up to 250ms, There are ways to (at least partially) get around this, but it's not worth the trouble given the higher voltage loss (and dissipation) of a MOSFET vs. BJT circuit.
When this is combined with the greater voltage loss (typically 5V or more depending on the MOSFET and load current) and the correspondingly high dissipation, it is a sub-optimal solution. Using a MOSFET may seem 'high-tech' compared to lowly BJTs, but they cannot perform as well, and the less-than-ideal SOA of a MOSFET operated in linear mode.
This is something that hasn't been used as far as I'm aware. There are many caveats of course, mainly due to the high voltages used in valve (vacuum tube) designs. I've not tested or even performed detailed simulations for a high-voltage version, but with the right transistors it should be possible to get a very clean supply. The greatest issue you'll have is finding devices that can handle the voltage and remain within the safe operating area of the series-pass transistor. This is probably an area where a MOSFET is the best choice, provided the SOA is not exceeded.
An IRF840 can provide up to 400mA even with 300V between drain and source, so charging output capacitors shouldn't be a challenge. An output of 1A at 400V is well within its capabilities, which is more than enough for 4 x KT88 output valves. I leave this as something to ponder, as I don't have any high-powered valve amps that are amenable to this type of modification. It could be done of course, but mostly I don't use the valve amps I have, and certainly don't intend to make any serious modifications that will take considerable time for no direct benefit.
The circuit doesn't change much, but all resistor values are increased, capacitor values reduced, and a gate protection zener diode is essential. There is no doubt whatsoever that a well-engineered capacitance multiplier will provide less ripple and better overall performance that the common C-L-C filter commonly used, but people who build valve amps generally prefer 'traditional' techniques, and will avoid using transistors (or any other semiconductor) as a matter of principle.
I must say that I find this more than a little depressing. The idea of engineering is to use the best solution to a problem, and if that means using some semiconductors in a valve amplifier if it improves performance, then that's what should be used. There's nothing 'magic' about valve rectifiers (quite the opposite in fact), and if a capacitance multiplier or regulator gives lower ripple and better performance than an inductor, then that's the optimum solution. It's a different matter if it's a restoration, since originality is a requirement, but for a new build you should use the best circuit for the task. If that means a hybrid of valves and transistors, then so be it (and it will be cheaper as well as performing better).
A capacitance multiplier isn't the only way to get very low ripple. In valve amplifiers, filter chokes (inductors) are still very common, and ripple attenuation is good, but far from perfect. The so-called 'pi' filter (so named because it resembles the Greek letter π) works well, and it suppresses ripple without excessive voltage loss due to ripple. For the example shown below, the ripple across C1 can be as much as 10V peak-peak, so the available voltage is less than 28V DC at 3.2A output with the lowest voltage determined by the ripple. Adding a filter choke of only 100mH raises the minimum voltage to 33V with the same current. The only other way to get a higher average DC output is to use a much larger filter capacitor (at least 10mF).
For the example shown below, the transformer has a loaded output voltage of 27.5V AC, with a DC output of 31.8V at 3.18A (10Ω resistor). Without the resonant filter (no inductor and capacitor, but with 2 x 2,200µF filter caps) the output ripple is 1.5V RMS, or 4.74V peak-to-peak (p-p). The DC output is a little higher because there's no series resistance, so the voltage is 32.5V at 3.25A.At 100Hz (rectified 50Hz), the 100mH inductor has an impedance of 62.8Ω, but (at least for this example) a resistance of 0.1Ω. This was used for simulation, but in reality the resistance will be considerably higher. Without CR (the parallel resonance capacitor) ripple is reduced to 33mV RMS (95mV p-p). Adding CR reduces this to 7mV RMS (23mV p-p, and at 200Hz). You may well ask why the frequency is doubled, and the answer is simple - the 100Hz 'fundamental' is all but eliminated, leaving only the 2nd harmonic. For the particularly fussy, you could add another parallel resonant filter, but tuned to 200Hz (50mH || 12.5µF).
You could be excused for thinking that CR would be subjected to high current, but it's not. Even with the maximum load used in the simulation (3.18A), the capacitor's ripple current is only 51mA. Of more concern is stability over the years, as electrolytic caps aren't known for short or long-term accuracy. For this reason, a film capacitor would be preferred, but this adds more cost and bulk. The inductor will be fairly substantial, as it must carry the full DC without the core saturating. While this approach appears to offer many advantages, they disappear quite quickly when you try to source the components. The values for LR and CR are critical for good performance. The frequency is determined by ...
f = 1 / ( 2π √ LC ) Alternatively, if you know the frequency and inductance, determine the capacitance ...
C = 1 / ( f² (2π)² L )
The tuning needs to be as close as possible to the ripple frequency, and the values shown are correct for 50Hz mains (100Hz ripple). For 60Hz mains, CR must be reduced to 17.6µF. Either value will need to be made up from paralleled caps, and fine-tuned to get resonance as close as possible to 100Hz or 120Hz as required. Don't expect the L1 to be exactly the claimed inductance, as tolerance is usually fairly broad (expect ±10% for commercial products). Adding the parallel capacitor should result in a ripple reduction of around 12dB compared to a traditional pi filter (with the same values for all other components).
Based on a simulation, the ripple without the resonant capacitor is 29mV RMS at full load (10Ω). With the resonant cap in circuit, this is reduced to 5mV, with the ripple frequency increased to 200Hz (50Hz mains). That's a reduction of 15dB. The notch filter created removes almost all 100Hz ripple, and the output consists only of the harmonics. The amplitude of these is not increased, but they are what's 'left over' after the 100Hz ripple is removed.
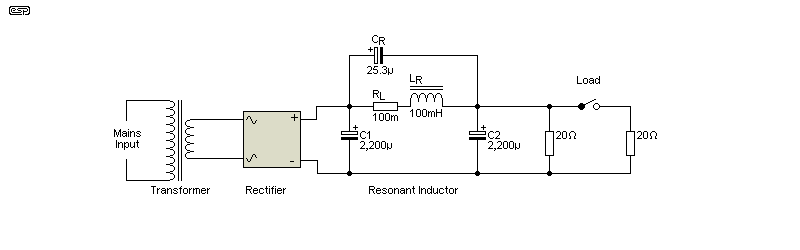
Figure 8.1 - Parallel Resonant Filter PSU
It's likely that many readers will wonder why this arrangement isn't used all the time, since it's so effective. The answer is quite simple, and it's almost certainly not what you want to see. Like capacitance multipliers, filters incorporating inductors are suitable for continuous loads. If the load current varies, the resonant frequencies created by the inductor, filter capacitors and/ or the resonance of the series filter interact to create unwanted peaks and dips as the load changes. With only an inductor, the resonant circuit consists of C1, L1 and C2, with the two capacitors effectively in series. Resonance therefore occurs at 10.7Hz, and the presence (or otherwise) of CR doesn't change this. While it may not seem possible to have two different resonant frequencies from a single inductor, it happens because the overall topology allows it - the 'basic' LC filter and the (deliberate) resonant LC filter tuned to 100Hz act independently of each other.
The step response was simulated by switching the second 20Ω resistor in and out of circuit at a 1Hz rate (500ms on, 500ms off). There's an initial 'spike' which rises to 48V (not shown), and it's expected with any filter using an inductor. This is often a 'deal-breaker' in itself, because the over-voltage can damage circuitry. The fact that the voltage dips to 25V when the load is applied and peaks to 40V when the load is removed is a characteristic of filters using inductors, so they are usually only suited to loads that either change slowly or not at all. Oddly enough, music usually changes slowly enough so that problems are usually averted. The resonant frequency must be lower than the lowest signal frequency of interest to prevent unwanted interactions.
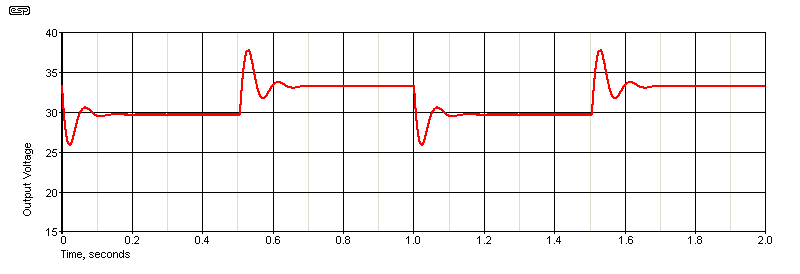
Figure 8.2 - Resonant Filter Step Response
The step response shown above is identical, regardless of whether CR is connected or not. For the simulation, the current was varied by a factor of two. At 'half' load (20Ω, 1.75A), the output voltage is 33V DC, falling to 29.5V with the full 10Ω load. One thing that an inductor or resonant filter can do is provide more DC voltage than a capacitance multiplier with similar performance. Because the inductor is reactive, it stores energy during peaks and releases it during troughs. You must be mindful of the resonance created by the inductor and the two filter caps. With the values shown, resonance is at 15Hz.
With just the two 2.2mF caps in parallel, the minimum voltage is 30.2V at 3A, and a capacitance multiplier would reduce that further. However, one must consider that the filter choke will be large, heavy and costly. This is the main reason they're not used in low-voltage, low-frequency power supplies. High-value capacitors are comparatively cheap and don't take up much space, and that's the approach that's used in almost all power supplies used for audio. Switchmode power supplies are a different matter, and the pi filter is very common to reduce output noise. The switching frequency is high, so the inductance needed is small, and it's common to see powdered-iron toroidal inductors in this role. Inductor-capacitor resonance peaks are (hopefully) dealt with by the feedback circuit.
This last version is an oddball - I tracked down where it came from [ 4 ], but the first I saw it was when it was sent to me by a reader who erroneously thought he'd seen it on my site. The idea is that the incoming noise is inverted and used to counteract the input noise, with the hope that it will be equal and opposite. This can only happen properly under very limited conditions, but it is an interesting approach. If the transistor and other circuitry is left out, leaving only the 15Ω resistor and 220µF capacitor (R1 and C4), the performance is almost as good.
Very low noise isn't needed for most audio work, as the amplifying device will usually be an opamp and these have good power supply rejection. For very low-level RF (radio frequency) amplifiers, getting ultra-low noise is often a requirement. There are several very low noise LDO regulators, but most have a limited input voltage (often no more than 5V). A noise-cancelling circuit such as that shown below might be useful, but a conventional RC filter will be sufficient in many (most?) cases. The original circuit does not include C4, which reduces the effectiveness rather dramatically, and may cause misbehaviour in the powered circuitry.
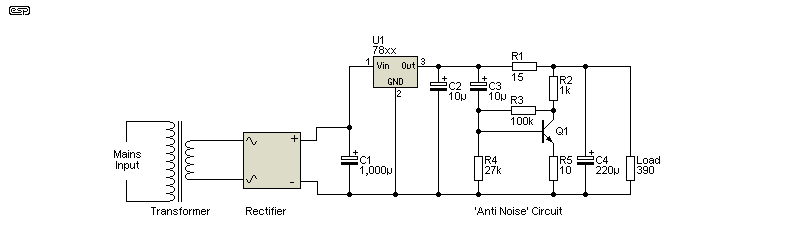
Figure 9.1 - 'Anti-Noise' Circuit
Q1 must be selected to suit the likely current, but for a nominal 15V low-current supply a BC549 should do nicely. The test load was 390Ω, providing a current draw of about 37mA. The output voltage was reduced by about 0.68V, as expected with the load and the current through Q1 (about 5mA). The circuit works by inverting the noise and feeding that back to the output such that the 'anti-noise' cancels the regulator's noise. If noise and 'anti-noise' are equal and opposite they cancel.
The noise reduction (at 1kHz) with the values shown was 23dB (without C4), and with only R1 and C4 that increased to just over 26dB. With both the 'anti-noise' circuit and C4, that was increased to 55dB. It's far simpler to use only a resistor (R1) and a bigger capacitor for C4. Alternatively, use an LM317 regulator, which is much quieter than the 78xx series. In theory, this circuit can achieve impressively low noise, but a simple RC filter is a great deal easier.
It's possible that some people may find this useful, and it's equally possible that no-one will bother. Performance can be improved by changing the values of R1 and R5, and it's also possible to boost the performance by using a more accurate inverter. In the end, you may be able to get a circuit such as this to almost equal a low-noise regulator, but with many more parts. It is possible to get complete cancellation of any ripple or noise, but the end result is far more complex than a cap multiplier or regulator, and it may be considered a waste of components.
A negative version can be made by using a PNP transistor, and reversing the polarity of all capacitors. One thing that this circuit does show is that it's possible to reduce low-frequency noise by inverting and summing it, so it's still an interesting technique. Ideally, the transistor inverter's gain will be made variable to allow complete cancellation. I've not bothered to provide any waveforms as I don't think the idea is particularly useful, but someone may find it suits their application. Then again ...
It's no accident that the suggested values shown here are the same as those recommended in Project 15. That design was used as the 'inspiration' for this article (including some of the original text), with the difference being that this goes into more detail for the design process. This includes proper transformer sizing and more accurate simulations than were available to me when the project was published.
As noted in the introduction, the term 'capacitance multiplier' is a misnomer. If that were the case, the gain (hFE) of the transistors (or MOSFET transconductance) would need to be factored into the equation to determine the filtering effect. That isn't the case at all, because all you have is a voltage follower (the transistors) fed by a passive filter. No part of the circuit qualifies as a 'multiplier'. The only place where the transistor's gain comes into play is when determining the resistor values, as low gain means that the resistors supplying base current have to pass more current (lower resistance). This means that caps have to be larger to get the same ripple reduction.
Capacitance multipliers aren't particularly common now, since most Class-AB amplifiers use dual supplies, and most have very good ripple rejection. However, for a Class-A amp or anywhere else that you need a very clean (ripple and noise free) voltage, they're hard to beat. Because the voltage drop across a cap multiplier circuit is low, there's very little heat to deal with, but of course the output voltage varies along with the input voltage. This includes the transformer regulation, which is always much worse than the datasheet figure because of the rectifier and filter capacitor.
A capacitance multiplier is not something that suits all circuitry, and this is especially true with dynamic loading. Therefore, I don't recommend that you use one with Class-AB amplifiers, because the current varies so much. A Class-A amp may have a 2:1 current variation, but for Class-AB it can be over 100:1 variation. This is not what capacitance multipliers are designed for.
The primary benefit of a capacitance multiplier is that you can almost eliminate ripple, without having to use insanely large amounts of capacitance. They have a relatively low voltage drop, at least compared to a regulator, and the output voltage follows the input voltage with both load current and mains variations. This may be seen as a disadvantage, but it happens with a simple capacitor filter too, but with increased ripple as the current increases. The multiplier provides excellent filtering at any output current within its design range, which is its primary reason to exist. A cap multiplier is not intended to replace a regulator, although the circuitry can appear almost identical to a simple zener diode regulated supply.
These circuits are not for everyone, and most of us don't need to use them. If you have a Class-A amplifier, you probably have a good reason to try using the one that meets your needs. The calculations are mostly pretty straightforward, but sizing the transformer will often be an issue, especially if it has poor regulation. The only way to improve this is to use a bigger transformer, as the regulation is inversely proportional to the VA rating. A cap multiplier stage can also be added to a regulator (in a bench supply for example) to reduce the ripple breakthrough.
1 JLH Capacitance Multiplier
2 The Capacitance Multiplier (AudioXpress, February 2021)
3 BD139/140 and TIP35/36 Transistor Datasheets
4 Finesse Voltage Regulator Noise! (Wenzel Associates)
 Main Index
Main Index
 Articles Index
Articles Index