
 |
| Elliott Sound Products | Beginners Guide to Logic |
 Main Index
Main Index Articles Index
Articles Index Logic ICs aren't what they used to be. In the early days, we had RTL (resistor-transistor logic) along with DRL (diode-resistor logic), DTL (diode-transistor logic), TTL (transistor-transistor logic), PMOS (P-Channel metal oxide field effect transistors - MOSFETs) then CMOS (complementary MOSFETs, both P and N-Channel). High speed circuitry used ECL (emitter coupled logic) which operated the transistors in the non-saturated (not turned fully on) to obtain higher speed. Before that valves (vacuum tubes) were used for either analogue or limited digital computers. They were limited because the number of valves needed became unrealistic, as did the power supplies needed to feed them electrons. As technology progressed, the size of components shrunk, until we now have a chip you can hold in one hand (with lots of room to spare) having millions of transistors.
It would be a pointless exercise to even attempt to describe the internals of a modern microprocessor, but the building blocks used to create the circuit perform the same jobs as the earliest circuits that were ever used. Likewise, it would not be helpful to try to describe how (very) early mathematical 'engines' worked. There were mechanical, with the best known being Charles Babbage's 'Analytical Engine' which was actually made operational by Ada Lovelace, and she is often regarded as the first 'computer' programmer. For anyone interested, this is a fascinating area, and formed the basis of modern computing as we know it today. The earliest computers were built using TTL logic, often helped by including a pair of ALUs (Arithmetic Logic Units), most commonly the 74181 (now long obsolete). These reduced the size of a basic computer from several large PCBs to just one (still large) PCB. I worked on these back when it was still economical to fix computer boards, during the mid 1980s.
The essential elements of any logic circuit are gates. These provide an output based on the voltage applied to their inputs, and the most common are the AND gate, OR gate and inverter (also called a NOT gate). There are many others as well, but these simple gates form the basis of most digital circuitry as we know it today. In order to gather and present data to and from the real world, there is also a need for analogue to digital converters (ADCs), and their opposites, digital to analogue converters (DACs). I don't propose to cover these here.
Most of the time, a logic 'low' ('0') is defined as being at (or near) zero volts. The logic 'high' ('1') voltage used to be 5V, but some CMOS ICs can use 15V, and many of the newer circuits use 3.3V or less (as low as 1.8V for many high density ICs). PMOS was really the 'odd man out' in all of this, because it used a negative supply voltage. All logic has a defined range where an input is accepted as a '1' or '0', and in between is no-man's-land. Voltages in this undefined region may be interpreted as a '1' or a '0', and good design ensures that all voltages are within the specified regions, except when switching from one state to the other of course. As logic becomes faster and faster, there are issues faced that take many digital designers well outside their comfort zone. This is covered in some detail in the article Analogue vs Digital - Does 'Digital' Really Exist?.
All of the circuits shown in this article can be built on a standard plug-in breadboard, or wired on Veroboard. Readily available transistors are used throughout, and any small signal NPN transistor can be used in any of the demonstration circuits. Mostly, you don't need to bother, because the operation of most is (almost) self explanatory if you understand basic transistor theory.
There are a number of different 'families' of logic. Standard TTL is generally prefixed by 74, with a 7400 being a dual 4-input NAND gate. 74L series are low-power versions, 74LS are low-power Schottky. Military or extended temperature range TTL is prefixed by 54, and TTL compatible CMOS uses 74HC or 74HCT numbers. Basic CMOS is usually designated as the 4xxx series, but there are many variations. The basic logic families are as follows ...
RTL Resistor Transistor Logic ¹
DTL Diode Transistor Logic ¹
TTL Transistor Transistor Logic
ECL Emitter Coupled Logic
PMOS P-Channel Metal Oxide Semiconductor ¹
CMOS Complementary Metal Oxide Semiconductor Logic
Those shown with '¹' are now obsolete. Two that continue in discrete form (generally for DIY projects) is DRL (Diode-Resistor Logic) and DTL, which is often used to create simple AND/ NAND and OR/ NOR functions. it's not particularly efficient and is usually slow, but for some simple tasks that's of no consequence.
Most logic circuits can be described by a 'truth table', which for a NAND gate looks like that shown below. I also included 'pseudo code', which is not intended to be seen as being in any specific programming language, but describes how the function would be implemented in code. 'DIM' means dimension, and 'BOOLEAN' (often abbreviated to 'BOOL') is a (usually) single bit that can be '1' (aka 'True') or '0' (aka 'False'). Some languages allow numerical values ('0' or '1'), others insist on 'true' or 'false'. The 'IF...THEN...ELSE' format is common to many different languages, but formatting may differ. In some languages, an 'ENDIF' statement is required to delineate the 'IF...ELSE' from other code ('THEN' is not required by all languages, or may be optional).
A B Y 0 0 1 1 0 1 0 1 1 1 1 0
DIM A, B, Y as BOOLEAN
IF A=1 AND B=1 THEN Y=0 ELSE Y=1
This is convenient for small logic devices, but becomes unwieldy very quickly with more complex gate arrays or other highly integrated logic circuits. For example, the truth table for a modern microprocessor could end up being almost infinite if every possibility of input and internal states were to be documented. Many datasheets include the truth table, and often have graphs to show the timing requirements - particularly for latches, counters, shift registers, etc. Many of these have a minimum 'set up' time, where (for example) data must be present for a small period before the clock signal is applied.
Internal circuits are shown only for TTL, because CMOS circuits are usually much more convoluted, and are difficult to build if you want to see how they operate. The internal circuits are not widely available, and tend not to provide an easily understood operation. In contrast, TTL is straightforward, there are many circuits on the Net, and they are (mostly) easy to understand if you have some basic transistor theory knowledge. The component values shown below are from the standard E12 series, and are not the same as shown in datasheets. The difference is minimal.
Over the years there have been countless TTL functions, but a vast number of those are now obsolete. Most of the old memory ICs are no longer made, and they were only common during the time where computers were built using TTL logic to build the processor itself. These are now fully integrated, ranging from PICs (Programmable Interface Controllers) through dedicated microprocessors and ending with the latest multiple core processor chips used in PCs, tablets and high end mobile phones.
All logic circuits suffer from propagation delay. Modern fabrication techniques use lower voltages (as low as 1.8V in some cases) which allows the logic to draw higher current for the same or less power consumption. Speed is always a function of power - if you want to go faster, you need more power (or in this case, current). As an example, the CMOS 4040 counter IC (more on this further below) has a propagation delay of up to 330ns with 5V, 160ns at 10V or 130ns at 15V. The difference is due to the current drawn - higher voltage, higher current.
Propagation delays occur because nothing is instantaneous. Transistors can't turn off instantly, as it takes time for the carriers in the doped silicon to disperse to the point where the transistor is truly off. This is made worse with TTL, because the transistors are driven to saturation (more base current than necessary to turn the transistor(s) on). ECL (Emitter Coupled Logic) overcame this by operating the transistors in their linear range (neither fully on or off), and while that increases speed, it reduces noise immunity and increases power consumption. To provide a bit of 'nuisance value', ECL uses a negative supply, with the positive supply rail being earth/ ground.
There are countless compromises in all electronics, and logic is no different. CMOS is now the dominant technology, and is used in nearly all processors, from basic PIC microcontrollers up to the VLSI (Very Large Scale Integration) required for processors (including graphics processing), ASICs (Application Specific ICs, generally custom made for a particular purpose) and FPGAs (Field Programmable Gate Arrays). The latter can be configured to perform complex tasks very quickly, and are programmed by the customer/ end user to perform specific tasks as efficiently as possible. They are well outside the scope of this article!
There are CMOS variants of many of the 74 series TTL ICs, generally prefixed with 74HC... or 74HCT... The 'HCT' types are designed to be compatible with 74 series TTL, and cannot be used at the higher voltages common to the 4000 series of CMOS. 74HC types often allow (a bit) more than 5V, but that varies, so you must consult the datasheet. Making assumptions is unwise. If you need the full 15V (18V absolute maximum) CMOS ICs, then you need to stay with the 4000 series.
There isn't a digital circuit that doesn't use one or more of these basic gates. They are the basis for all 'higher level' functions, and the outcome is (in logic terms) either true ('1') or false ('0'). Boolean algebra is only mentioned in passing here, but it's the basis of modern computing - which is in turn based on the three functions AND, OR and NOT. Boolean algebra was first developed by English mathematician George Boole, and was described in his first book 'The Mathematical Analysis of Logic', published in 1847. To learn more on the topic, I suggest you check out the Wikipedia page, which goes into much greater detail.
The premise of an AND gate is that the output will be high (logical '1') only if both inputs are high (input1 AND input2). A NAND gate will output a logic '0' under the same conditions (Negative AND). Although IC designers can do 'odd' things (such as build a transistor with multiple emitters), this can't be directly translated to a breadboard. The circuits shown can be built on breadboard, and they are presented in a way that makes it easy to do.
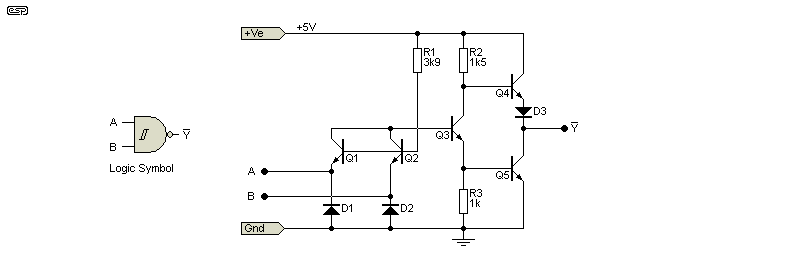
Figure 1 - TTL NAND Gate
Q1 and Q2 are shown as separate transistors, but in reality it's a single transistor with two emitters. Performance is the same either way. The output will go low when and only when both inputs are high. That means that the output is Negative, when 'A' and 'B' are positive. The circuit is therefore a NAND gate. An AND gate is created by adding an inverting stage between Q1/2 and the totem-pole output transistor driver (Q3).
Q1 and Q2 use their emitters as the input. When the emitters are held low, the transistors both conduct, and bypass the base current for Q3 (provided by R1) to ground. Q4 is turned on via current through R2, and Q5 is off because there is no voltage across R3. This condition exists if either input is low, so the output is high. When both Q1 and Q2 emitters are high, Q3 turns on. This forces Q4 to turn off, aided by D3 which ensures that all current through R2 is diverted from the base of Q4. Q5 conducts fully, and the output is low. In common with most logic circuits, there is a comparatively high current drawn during the transition from high to low and vice versa, and this is why bypass capacitors are required for all logic circuits.
Commercial ICs can have more than two inputs, with 4 inputs being common for AND/ NAND and OR/ NOR gates. Another option is open-collector outputs, which allow TTL to interface with CMOS using a different supply voltage (higher or lower than 5V), or to permit connection to other circuitry. Open collector outputs are generally able to handle more than the normal 5V supply, with up to 30V being fairly typical. There are specialised open collector ICs that are designed for driving small relays, and they include the back-EMF diode required with relays.
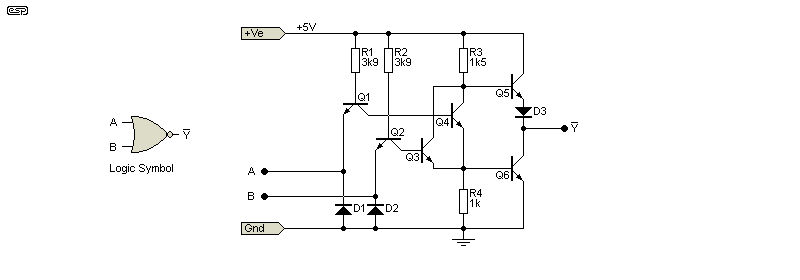
Figure 2 - TTL NOR Gate
A NOR gate is somewhat more complex, even though (at least in theory) it's a simpler function. If 'A' or 'B' is high, the output is low. Like the NAND gate, an OR gate is created by adding an inverter between Q3 and Q4 (which are in parallel) and the totem-pole output stage. Operation is very similar to that for the NAND gate, except that Q4 is turned off if either or both 'A' or 'B' is high.
A B Y 0 0 1 1 0 0 0 1 0 1 1 0
DIM A, B, Y as BOOLEAN
IF A=1 OR B=1 THEN Y=0 ELSE Y=1
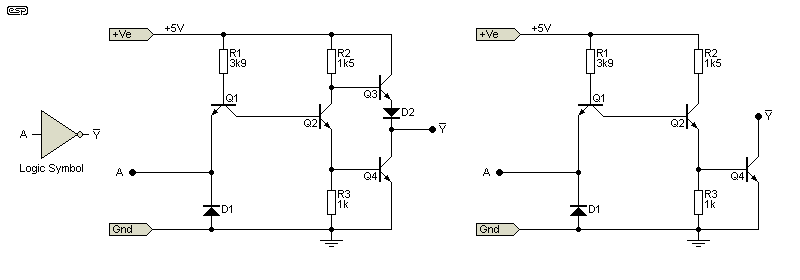
Figure 3 - Inverter (NOT) Gate
The inverter is a simple function, but its importance in logic cannot be underestimated. As noted above, AND and OR gates require inversion to get the required function from NAND and NOR gates respectively. So many logic functions rely on inversion that we'd be lost without them. An open collector version is also shown for the inverter (the transistor numbers are kept the same so it's easier to follow).
If you are working with any logic circuitry, it's not uncommon to find that you need a simple method to include a simple OR or AND function (or its inverse). Often, it's easiest to use a few diodes and a resistor, optionally with a transistor. This can be used to decode a simple sequence from the output of a counter or shift register, and can save the hassle of including another IC where you may only need a single gate.
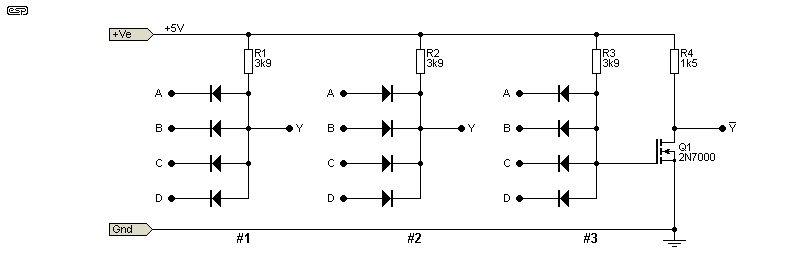
Figure 4 - Diode Logic Examples
In the above (#1), the output will be low if A, B, C or D (or any combination thereof) are low. In other words, it's an AND gate, requiring that all inputs are high to give a high output. The second circuit (#2) is an OR gate, so the output will be high if any input is high. Finally, circuit #3 is a NAND gate. It's the same as #1, but the output is inverted by Q1 (a small signal MOSFET).
These circuits can be intermingled to get some interesting combinations, and there is no practical limit to the number of diodes used. In some cases, it can be convenient to connect the input resistor (3.9k) to the output of another gate, allowing some quite complex logic functions to be created that may require several TTL or CMOS gates. The circuits are all shown with four inputs, but you can use more or fewer, depending on what you wish to achieve. Surprisingly, this technique is still useful (although it's very slow compared to 'real' gates), and was the basis for some of the earliest logic.
It can be put to use anywhere you need a simple way to decode the output from a counter or shift register, or if you happen to need a odd function that isn't readily available with existing gates. As shown, you can't use a bipolar transistor for Q1, because the forward voltage of the diodes will prevent it from turning off properly. You could use a Darlington transistor for Q1, but that has a higher saturation voltage, but should still work with TTL.
Some of the basic TTL and CMOS circuits are available with 'Tri-State' outputs. The third state is 'output disconnected' - the output is neither on nor off, but is floating (high impedance). This is used so the different systems can use a common data bus, and only the selected device provides a signal to the bus. This is known as multiplexing, where several different data streams are transmitted over a single wire or PCB trace. The devices that are transmitting and receiving data are active, and other devices that share the bus wait for their turn. This is a very common requirement as it can save a great deal of extra wiring and/ or PCB real estate than providing a conductor for every data stream. However, it's also slower because each section has to wait until its turn to transmit and receive data.
Another function is devices with Schmitt trigger inputs. These are used primarily for greater noise immunity, but with CMOS logic, Schmitt trigger inputs are often used to create simple R/C (resistor capacitor) oscillators and timers. They are not precise in either role, but that's often a secondary consideration. Not all logic has to have especially precise timing, and where this is necessary more complex circuitry is required.
One final 'basic' gate that can't be ignored is the 'exclusive OR' (XOR). This gate provides a 'high' output, only when the two inputs are different. If both are high or low, there's no output, but if either input is the opposite of the other, an output is produced. The truth table is shown below. Note that '!=' means 'NOT EQUAL' - this may vary with different programming languages.
A B Y 0 0 0 1 0 1 0 1 1 1 1 0
DIM A, B, Y as BOOLEAN
IF A!=B THEN Y=1 ELSE Y=0
The aim of this is to detect if two logic levels are different from each other. There's also an XNOR gate and there used to be a gate where the user could select XOR or XNOR operation (74x135, now obsolete). With CMOS, an XOR gate is often used as a 'zero crossing detector', designed to produce a brief output pulse whenever a logic level changes. It works equally for rising and falling edges.
A function available in CMOS is an analogue switch. The 4066 is a quad bilateral switch, and can pass analogue signals that are between the two supply rails. It's not uncommon to see them used with ±7.5V supplies so ground referenced audio signals can be turned on and off. The original version was the 4016, but that had much higher 'on' resistance, which could mean signal distortion from high impedance sources. These switches have interchangeable analogue inputs and outputs, and have a control pin for each switch (as well as the required VDD positive and VSS negative supply.
These have no equivalent in any other type of logic - they are unique to CMOS. While it's difficult to classify them as 'audiophile' devices in terms of signal integrity, they have been used in a great deal of audio equipment because they are easily controlled with other logic, although if operated with ±7.5V supplies, level shifting is necessary. The information in the datasheet is very comprehensive, and if this sounds like something you need then they are easy to use and ideal for audio switching. Don't expect especially low noise or distortion (relays are far better in these respects), but they are very low power (like nearly all CMOS) and are not affected by vibration, unlike relays.
There are newer analogue switches that beat the 4066 in almost every respect, but like so many modern devices, many are only available in SMD packages. Where the 4066 has been around for decades, the same can't necessarily be said for the newer devices. One thing to be wary of is the specific type number. The 74HCT4066 is designed for an operating voltage of 5V, not 15V as is normally expected. The 74HC4066 is rated for a maximum supply voltage of 10V. You always need to be careful with any 74HC prefix CMOS ICs, and verify the supply voltage before you apply power.
This is where 'complex' logic starts. They are essential building blocks in any logic system, and operate as 'short-term' memory of a past event, or to store data, divide frequencies, etc. For example, in a multiplexed system, a latch of one kind or another is necessary to 'remember' the data that was passed by a sub-system within the circuit. 'Flip-flop' is an old term, but it has managed to live on, regardless of technological progress. It's derived from the fact that the outputs can flip from on state, then flop back again with the appropriate input.
Of these, the simplest is the 'set/ reset' latch. A signal on input 'S' (Set) causes Q2 (Q) to go high, and Q2 (Q-Bar, Bar-Q or NOT-Q) to go low. A signal on input 'R' (Reset) causes it to revert to the original state. Note that latches and counters generally use the term 'Q' to signify an output, and 'D' to indicate data. Set and Reset (aka Preset and Clear) pins are used to ensure that the latch is in a known state when the system is initialised (powered on or reset). The simplest 'true' latch is the D-Type, which uses a clock signal to load the level present on the 'D' input into the latch.
An example of a set/ reset latch is shown below. It's not intended to follow normal TTL input and output conventions, but is implemented with two transistors. This is a 'level triggered' circuit, which means that it responds to the level of the input, and isn't affected by the rate of change of the signal. The other triggering system is 'edge triggered', where the logic IC relies on a rising or falling signal, with a defined polarity (rising or falling). For example, a rising edge triggered flip flop is only triggered on a rising edge (from '0' to '1') and it ignores the falling edge ('1' to '0').

Figure 5 - Set/ Reset Latch (Bistable Flip-Flop)
The other latch that's been used for many years is the 'master/ slave' J-K flip flop. These are the most flexible of the latches, and are common in MSI (medium scale integration) to create counters. Counters are a special case in all logic, and it's outside the scope of this introductory article to try to cover them in any detail. However, a basic counter is shown below.
D-Type flip-flops are very common, and the value of the signal on the 'D' (data) input doesn't cause any change until the clock transitions (usually from low to high). The value of the 'D' input is then provided at the Q output, and the opposite polarity on the Q-Bar output. If 'D' is a '1', then Q is also a '1' and Q-Bar is '0', and vice versa.
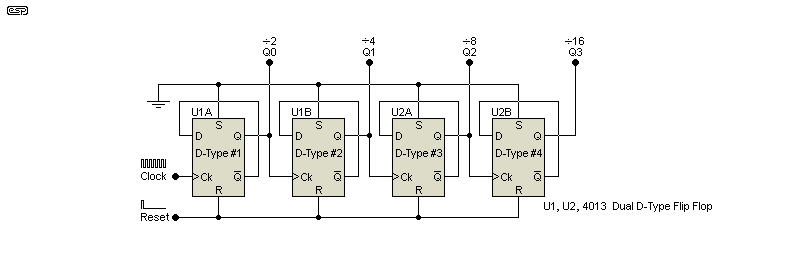
Figure 6 - 4-Bit Asynchronous Counter
The input signal is applied to the Clock (Ck) input of D-Type #1, and is divided by two with each successive flip flop. At the end, the input frequency is divided by 16 (24), so if a 16kHz signal is applied to the clock input, the output is a 1kHz squarewave. This is the binary sequence in a nutshell, and while it may initially seem that large numbers would require a vast number of flip flops, consider that using eight divides by 256, and using 16 divides by 65,536,000 (64k in binary). A CMOS 4040 is a 12-stage ripple counter (using the same basic architecture as that shown above), and using just two in series will divide by over 16 million.
Intermediate division ratios are usually provided by the use of NAND gates to decode the binary sequence to obtain the ratio needed. An example of this can be seen in the Frequency Changer (Figure 4) in the clocks section of the ESP website. To obtain a divide by five function, a CMOS divider is used. When both Q2 AND Q3 are high, the counter is supplied with data of the opposite polarity. There are many different ways these 'odd' division ratios can be created. While the trend these days is to use a PIC to handle reasonably complex division ratios, sometimes standard logic is a better alternative.

Figure 7 - 4-Bit Synchronous Counter
A synchronous counter doesn't suffer from accumulated propagation delays, as does an asynchronous (aka ripple) counter. However, there's a price to be paid, because the logic is more complex. J-K flip flops are used (aka 'master/ slave') and to get the same division, a pair of AND gates is required. Instead of the clock signal being passed along from one to the next, it drives all the flip flips simultaneously. This can be critical in some applications, where the propagation delay may cause invalid logic states (often called glitches). J-K flip flops mostly use a negative reset, so taking the reset pin to ground resets all flip flops to the same state. This isn't always necessary.
On the subject of clocks, a standard quartz crystal clock has a 1 second impulse (i.e. one second for a complete cycle). This is derived from a 15-stage binary counter, using a 32.678kHz crystal, which although it may seem like a very odd number, is designed specifically for the purpose of providing the timing for a quartz clock movement. See Clock Motors & How They Work for details of how these are designed. The waveform shown below applies to both the synchronous and asynchronous counters. The accumulated propagation delay is not visible, so the two look identical.
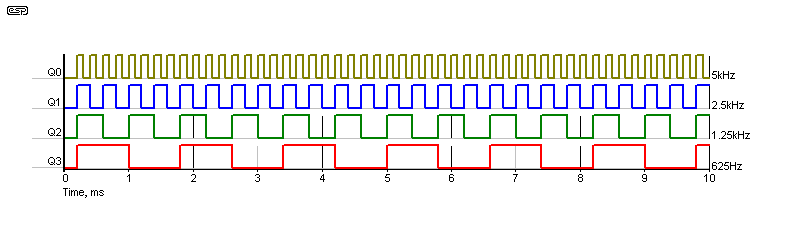
Figure 8 - 4-Bit Counter Waveforms (10kHz Input)
Another 'interesting' use for binary counters is shown in the Digital White/ Pink Noise Generator project. This uses cheap ICs (4094 CMOS 8-bit shift registers) with feedback (derived from an XOR gate) to provide a pseudo-random binary sequence that resembles white noise. While this can be done with a PIC, tat provides only a lesson in programming, but does little for one's understanding of the circuitry.
This has (sneakily) introduced another fundamental logic building block - the shift register. These look at bit like counters, but they pass data from the input to the output in the same pattern as it was received. An old term for them was a 'first-in, first out' register, and they are commonly used as a buffer, often to 'clean up' a data stream that was received with inaccurate timing. The data is loaded into the buffer, and read out with the exact timing expected by the following circuitry. They come in various configurations, and can be operated as serial in, serial out; serial in, parallel out; parallel in, parallel out or parallel in, serial out. They are also used to shift a digital byte or word left or right by 'n' digits.
A variation on the theme is called a Johnson or 'twisted ring' counter. These are something of a special case, as the output from each flip flop is the same frequency (determined by the length of the counter). A 5-stage counter will divide by ten, but the pattern of the outputs becomes the defining factor. In the article Sinewave Oscillators - Characteristics, Topologies and Examples (section 8) there's a Johnson/ twisted ring counter shown, and its outputs are summed to produce a crude sinewave. This can be filtered (and/ or more stages used) to improve the distortion characteristics.

Figure 9 - 4-Stage Johnson Counter
The term 'twisted ring' comes from the arrangement of the feedback. The output from the final Q-Bar output is fed back to the 'D' input of the first flip flop, so the bit pattern is shifted right one step for each clock cycle. The output is shown below. It's necessary to apply a reset to ensure that the counter starts with a defined state. D-Type latches are edge triggered, so only the '0' to '1' transition advances the cycle. There is also a ring counter (without the twist), and that requires that the first flip flop is set or it will be undefined, and may output zero forever. More than one flip flop can be set at power on, which provides specific sequences.
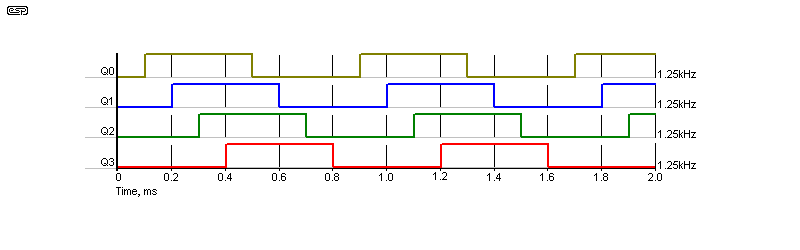
Figure 10 - 4-Stage Johnson Counter Waveforms (10kHz Input)
The truth table for a Johnson counter is shown below. At the 8th clock cycle it's back to the beginning, and the sequence continues as long as the clock signal is active, and the reset line remains disabled. To get a predictable output sequence, a Johnson counter requires a reset to each flip flop upon power-on. All ring counters are shift registers, with the data shifted from one to the next in order. Shift register ICs are also available with 'shift left' and 'shift right' control inputs.
4-Stage Johnson Counter Truth Table
CK # Q0 Q1 Q2 Q3 0 0 0 0 0 1 1 0 0 0 2 1 1 0 0 3 1 1 1 0 4 1 1 1 1 5 0 1 1 1 6 0 0 1 1 7 0 0 0 1 8 0 0 0 0
You can see that the waveform from each output is the same, but shifted in time from one to the next. The delay between each transition is one clock cycle. Since the clock used was 10kHz, each waveform is delayed by 100µs referred to the previous output. The positive signal lasts for 400µs, with a full cycle completing in 800µs (1.25kHz).
In many cases, a logic gate is not as it seems. Designers have long used the idea of inverted logic to obtain the results required using the smallest number of gates. If a NAND gate is used inverted (so inputs are normally high), the result is an inverted logic NOR gate. If In1 or In2 is low, the output is high. Likewise, an inverted NOR gate becomes a NAND gate, where both inputs must be low before the output can go high. This is generally covered using Boolean algebra, which can be used to determine the gates needed for the required truth table.
I don't propose to say too much on this, as it's often used without the designer even realising that negative logic has been used. It can save many gates in a complex circuit, but these are becoming less and less common with the wide usage of microcontrollers (such as PICs and other small processors). Things that used to be done in logic are now easily programmed, with a myriad of devices to choose from. 'Hard' logic is almost a thing of the past, but a surprising number of simple tasks still use basic logic ICs. An equally surprising number of simple tasks that could be done easily with a few gates are now consigned to a PIC, because they are so cheap. If the logic doesn't work as planned, you simply change the code until it does what you want.
Logic devices as we know them have changed radically since they were first used. Having gone from mechanical systems (some of which lasted until the 1970s or so), valves, discrete transistors and then integrated circuits, only a few of the originally available logic ICs are still available. They remain is use for the simple reason that they work, and are extremely reliable. System complexity has increased exponentially since the early days, and Moore's Law (named after Intel co-founder Gordon Moore) states that the number of transistors in ICs doubles every two years, and that the end result is cheaper. While there are rumblings that Moore's Law is 'dead', it seemingly refuses to lie down.
Most people carry far more computing power in their pocket than was available for the first moon landing craft, and a modern PC (of any 'flavour') is vastly more powerful than machines that used to occupy entire floors of large buildings. Data centres have hundreds or thousands of high-end machines, with storage capacities that are mind boggling. When I first started using computers, the standard machine was 8-bit, had 64k of RAM, typically a Z80 or perhaps 6800 series microprocessor, and booted from a floppy disk (remember them?). A 10MB hard disk was (literally) the size of a domestic washing machine, and if you needed a lot of storage you had to use tape drives that could take several minutes to find the data you were searching for.
Early processors such as the somewhat revered PDP11 made by DEC (Digital Equipment Corporation) started life in 1970, and quickly became the machine of choice for engineering and science. Meanwhile machines like the Datapoint 2200 (launched in 1970, and the first desktop machine that could (almost) be classified as a PC) captured a great deal of the business sector. The CPU was built entirely from standard logic ICs, and its instruction set (machine code) was the basis of the first microprocessor chip, the Intel 8008. I have rather fond memories of various Datapoint machines, as I worked for the company for about eight years.
 Main Index
Main Index Articles Index
Articles Index