
 |
| Elliott Sound Products | Balanced Inputs - Part IV |
 Main Index
Main Index Articles Index
Articles Index The single opamp balanced input stage (aka differential amplifier) has created a great deal of controversy during its life, and some people remain baffled by it's apparent odd behaviour. Indeed, when one analyses the circuit it is hard to imagine that it can perform properly, because the input impedance changes depending on how it's used. You only need to build one and test it to discover that it works just as claimed, but that's never convinced everyone. Anyone who's used a variety of sources will be aware that the voltages on the two inputs are often widely different under some conditions. This is often used as a reason to avoid it altogether, but that would be a mistake.
I will try to 'de-mystify' the circuit in this short article, in the interests of ensuring that its somewhat tarnished reputation is at least partially restored. The circuit is shown in the next section, and most readers will recognise it instantly. The misconceptions are all about input impedance, which is different for each input when it's connected to a source.
In the 'Designing With Opamps' article, I made the point that an opamp will, via the feedback path, make both input voltages the same (I call this 'The 1st Rule Of Opamps' - see Designing With Opamps). With any linear circuit, this relationship will always be true. Once you understand that one simple rule, you can analyse any linear circuit with confidence. The 2nd rule isn't relevant here, as it only applies when the 1st rule can't be satisfied, meaning that the circuit is non-linear.
In the following drawings and explanations, all resistors are 10k. This is done purely for ease of calculation, and the gain is unity. These circuits are used with gains both greater and less than unity, which simply means that the ratio of the input and feedback/ ground resistors is changed. The requirement for less than unity gain is uncommon, but there are situations where it's needed. Most readers won't have an immediately obvious application for less than unity gain, but it's worth remembering that it can be done.
Where the lowest possible noise is required, the resistor values should be reduced. Be aware that many opamps cannot drive very low impedances, so if you reduce the resistor values too far, you'll get higher distortion or even premature clipping as the opamp runs out of current. For most 'ordinary' opamps, the minimum resistance is around 2.2k, but you can use less with devices designed to drive 600Ω loads.
There's a persistent myth that the shield has to be impervious to RF (radio frequency) signals. The reality is that even a rudimentary shield will usually suffice, because the RF signal is impressed onto the shield, not the conductors. Poor grounding practices can lead to induced shield current being injected into circuitry, causing noise. This was particularly prevalent with early mobile (cell) phones. Few (if any) audio circuits can amplify the frequencies involved, but they can (and do) form rudimentary RF detectors. The noise heard is not the RF itself, but the envelope (the modulation 'pattern') of the RF waveform.
The circuit for the differential amplifier is found almost anywhere on the Net. It's also used for subtraction in analogue computer (and other) systems, and an example of it in this role can be seen in the article Subtractive/ 'Derived' Crossover Networks. The circuit is a useful tool, and is used in a wide range of different applications. As with any differential amplifier, the low-frequency common mode rejection ratio (CMRR) is almost completely determined by the accuracy of the resistors used. The theoretical worst case CMRR is 40dB with 1% resistors.
The most basic differential stage is shown below. This circuit (albeit in more advanced form) is the front-end of most opamps, and although it's shown using BJTs (bipolar junction transistors) it can also use JFETs (junction field-effect transistors), MOSFETs (typically in CMOS ICs) and valves (vacuum tubes). Because it operates without feedback it has limited use as shown, but a fully developed version can be seen in the Project 66 microphone preamplifier.

Figure 1.1 - Basic Discrete Differential Amplifier
This circuit is not without problems, as the output voltage is restricted (<1V from each output) before problems arise. With the values (and transistors) shown, the gain is around ×9.4, or 19dB across the two outputs. There's some emitter degeneration, and distortion performance is good with input levels below 100mV. This arrangement is used as the input stage of opamps (and many power amps - the circuit should be very recognisable). The output should ideally be obtained as current, not voltage, and when it's provided with feedback linearity is a great deal better. CMRR is very high, but only with perfectly matched transistors and resistors (R4, R5, R6 and R7), and when the output is taken from both outputs (requiring another differential amplifier). All parameters are improved once a voltage gain stage is added and feedback is applied. Note that the values shown are only as an example, and that overall performance is very limited if the output is single-ended.
When a high-gain opamp is used, everything falls into place, with predictable gain and a high CMRR (assuming close tolerance resistors). If you need a very high CMRR, the PCB traces are important too. Their resistance is (usually) not an issue, but stray capacitance can cause issues at high frequencies if you're not very careful. The opamp also causes a degradation of CMRR at high frequencies, as its open-loop gain falls with increasing frequency. This topic is covered in some detail in Balanced Inputs & Outputs - The Things No-One Tells You.
The following drawing is adapted from the Design of High-Performance Balanced Audio Interfaces article, and shows the conditions for various input configurations. The output voltage is indicated with a '+' or '-', meaning it's not inverted or inverted respectively. Note that the input impedance of the 'X' (non-inverting) input is always 20k, as there are two 10k resistors in series. The input impedance of the opamp is so high that it's irrelevant. There is one connection that's missing though, and that's the one that causes people so many problems. So, which one is missing? The condition where the differential inputs are earth/ ground referenced. While you might think this is unusual, it's actually the case for the vast majority of sources. This is covered in the next section.
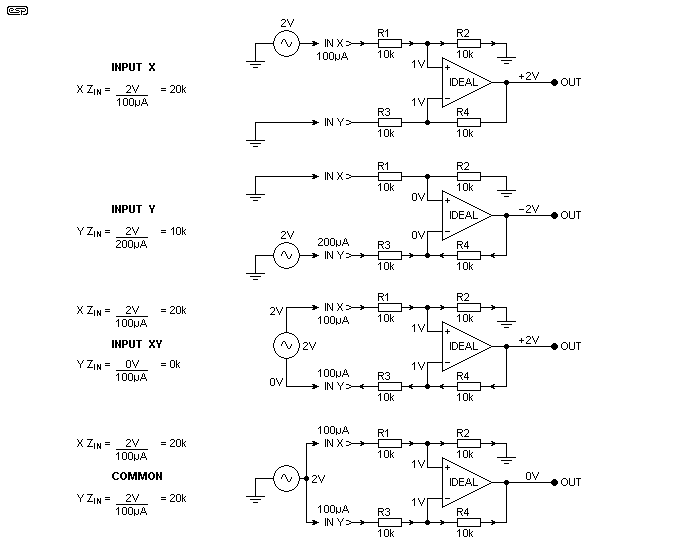
Figure 1.2 - Four Input Conditions For a Differential Amplifier
With a floating input source (Input XY), the voltages shown might seem impossible. Circuit analysis shows that in this case, the attempt by the source voltage to provide a negative current into Input Y results in the voltage at that point being zero, because 1V must exist across R3, and it's balanced out by the 1V at the opamp's inverting input. You need to examine the direction of current flow, indicated by the arrows. Having Input Y at zero volts is the only way that the opamp can be in its linear region, because both opamp inputs must be (very close to) the same voltage. 100µA flows through R3 and R4, so both resistors must have 1V across them.
By implication and calculation, this means that the input impedance at the 'X' input is 20k, and the 'Y' impedance is zero. While it's easy to assume that this compromises the circuit in some mysterious way, that's not the case. This is one of the reasons the circuit is criticised, with claims that it can't work properly because the impedances are unequal. Note that the conditions shown only apply at low frequencies (below 100Hz) because the gain of the opamp falls at higher frequencies causing the circuit balance to be affected. Performance is still acceptable up to 10kHz (perhaps more, depending on the opamp used).
There is no doubt at all that this is difficult to get your head around, but it's real. The current through R3 and R4 is exactly equal, but of opposite polarity. This is easy to simulate, but much harder to prove by measurement unless you have access to a fully floating voltage source. A battery powered audio oscillator is one method, or you can use a transformer. With the latter, keep the frequency below 400Hz to minimise the effects of stray capacitance which will seriously mess up your measurements at higher frequencies.
When you analyse the circuit, it's important that the source impedance is as low as possible. Any resistance/ impedance in the source causes the gain to be reduced, because the external resistance is in series with R1/ R3. In general, the source impedance should be no more than 10% of the resistance of R1/ R3, resulting in a loss of gain of less than 1dB. Impedance matching is never necessary with audio signals (up to 20kHz) unless the cable is more than 2km in length (λ=c/f)¹. This is common with telephony, but not with audio installations.
¹ λ is wavelength, c is velocity and f is frequency. Cables should be less than ¼λ at the highest frequency of interest (20kHz for audio) when impedance matching is not used.
When the source is balanced, but earth/ ground referenced, things get a little awkward. Almost all electronic balanced line drivers have a ground reference whether you like it or not. This is due to the way they work, and you can't short one output to ground and expect the other to provide double the voltage. There are line drivers that will do just that (see Project 87, Figure 3 for an example), but because these circuits can be unstable, they are not commonly used.
Even a transformer can be grounded, usually with a centre tap. It's almost always a bad idea, but that's never stopped anyone from doing it. The disadvantage of a ground-referenced balanced output is that it almost guarantees a ground loop, and it's up to the receiver circuit to remove the unwanted common-mode signal due to slightly different ground potentials. The connection of the shield is critical, and is the #1 cause of the 'Pin 1 Problem', which has plagued audio installations for as long as balanced connections have been in use.
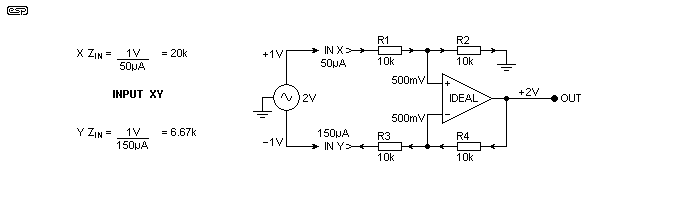
Figure 2.1 - Input Conditions With Ground-Referenced Source
The source is just shown as a 'centre-tapped' voltage generator, and is assumed to have a zero impedance at each output. This makes analysis easier, because adding external output impedances just causes headaches. Note that the source impedances must be equal! When used normally, the situation will be a little different from that shown, but it doesn't affect the operation of the circuit, provided the two output impedances are the same - the voltages do not have to be equal. As noted above, the 'X' input has an input impedance of 20k, and nothing external will change that. The 'Y' input impedance is less straightforward.
As shown, the 'Y' input impedance is 6.67k (rounded), and this is the only way that the opamp's linear operating conditions can be achieved. While it may all appear somewhat unlikely, the voltages shown can easily be measured or simulated, and the circuit behaves as we expect. The fact that the input impedances are not equal may seem like it will compromise CMRR, there is an important fact that is often ignored if the analysis is not performed rigorously.
The differential and common-mode behaviours are completely independent of each other. If you refer back to Figure 1, you can see that a common-mode signal is cancelled, because the same voltage appears on each input, and there is no output. This isn't changed if there's a differential signal present or not. So, a common-mode signal is rejected and a differential-mode signal is amplified, with the two functions remaining independent, regardless of any misconceptions that abound.
An easy way to get an effective increase in signal-to-noise ratio is to use a higher level. However, care is needed, because you have to allow enough headroom to ensure that peaks aren't clipped. In pubic address and studio work, it's common to use a reference level of +4dBu, which is around 1.23V RMS. If a peak to average ratio of 10dB is assumed (which is usually obtained only by using compression), the peak voltage will be 5.5V. Allowing a more realistic 20dB peak to average ratio, the peaks will be at ±17.4V. This is the reason that many professional mixers use ±18V supplies.
By default, most balanced line drivers double the level, since the same voltage is present on each conductor, but one is inverted. This improves the signal-noise ratio, but if the level is too high, the balanced receiver will clip. However, this is easily solved, simply by making the values of R1 and R3 higher than the values of R2 and R4.
If R1 and R3 are increased to 20k, the gain is exactly one, referred to the input of the line driver. However, in the interests of lower noise, it's better to reduce the values of R2 and R4 as shown below. The total voltage between the twisted-pair conductors is still 2V, but this arrangement lets you operate with higher gain without overdriving the receiver opamp. Remember that each wire in the pair only has 1V with respect to ground, but because one is 180° out-of-phase, the total voltage is 2V.
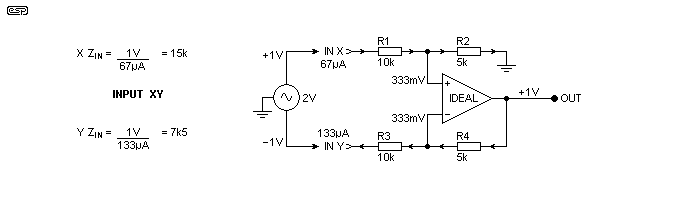
Figure 3.1 - Input Conditions With Reduced Gain
The voltages and currents are as you would expect, and this arrangement can be scaled for any input attenuation desired. The general operating parameters aren't changed, so it's performance is pretty much unchanged. Along with the reduction of level, you also get a better CMRR. With the values shown, it's improved by 6dB, which isn't spectacular, but it's worthwhile (and comes free!). If building this version, you'd use 5.1k resistors rather than 5k, and it will show a tiny gain (172mdB, or 0.17dB). This is inconsequential.
Naturally, the gain of the circuit can also be increased, but doing so will reduce the CMRR. The circuit is not really suitable for a microphone preamp, although many manufacturers have done so. One of the problems is that mic preamps need variable gain, and that's difficult to achieve with this particular circuit. A modest gain range can be implemented, but it requires positive feedback (which is rarely a good idea), and it can be improved with an additional opamp. This isn't covered here. Of course, R2 and R4 can be replaced by a dual-gang potentiometer, but that will seriously affect the CMRR because they never track perfectly, and have a wide tolerance.
With 10k resistors, an imbalance of just 10Ω between any two resistors will cause the 'ideal' CMRR to fall from 91dB to 66dB (simulated using a TL071 opamp). In reality, it's almost impossible to achieve the 92dB figure, as that requires better than 0.1% tolerance resistors (10Ω in 10k is 0.1%). However, countless differential amps have been made using 1% resistors, and that will typically allow a CMRR of better than 40dB. While that's a long way off the theoretical 92dB, in a typical application it's usually sufficient.
In reality, there's an external factor that often causes far more interference than a 'sub-optimal' balanced receiver's CMRR ...
Unfortunately, there is something between the sending circuit and the receiving circuit - the cable! If the common-mode performance is inadequate, the cable should be the first suspect. To ensure that CMRR is as high as possible, the shielded cable conductors must be twisted together to ensure that any noise injected into the wires is always equal. When used in what's laughingly called the 'real world', cables will be mistreated, and are regularly forcibly rolled into a 'convenient' format for storage. If this causes the twist to be deformed (and it will!), expect common-mode noise to be a problem because poorly twisted wires will not 'talk' to each other properly. They can then carry different currents from common-mode sources (mains leads and power transformers being the main sources).
In theory (always a wonderful thing), the shield isn't necessary at all. Data is most commonly sent between point 'A' and point 'B' via UTP (unshielded twisted-pair), with Ethernet being the most common data connection. The primary difference between the different categories (CAT3, CAT5, CAT5e, etc.) is the amount of twisting employed. There's also a requirement for the cable's impedance to be matched to the receiver, something that is not necessary for audio. These data connections are balanced, and there are specifications that state the minimum bending radius that can be used without (significant) loss of performance due to misalignment of the individual twisted pairs.
Unfortunately, some 'roadies' don't seem to understand how important it is to roll signal cables in such a way to ensure that the cable naturally 'falls' into place when being rolled up. Failure to do this can cause the twist to be disturbed, so parts of the cable don't have the correct internal geometry, allowing noise to be injected. It's not a problem with the balanced line drivers or receivers, but with the cable itself.
Despite any negative reactions you may read about this common circuit, the point that's often missed is that it does exactly what it says on the tin (as it were). While it doesn't seen 'right' in some respects, that's largely due to a misunderstanding of how it functions. The fact that it has unequal input impedances for the two input signals is immaterial, because it's input impedance for common-mode signals is identical. This is the only thing that really matters, and the way it works with a signal vs. common-mode 'noise' is perfectly alright. There is an expectation that the input impedance and signal level should be equal with a balanced line, and this holds perfectly true for common-mode noise. It doesn't matter at all for the wanted signal, and some signal sources do not have equal but opposite signals on both connections. This does not affect their performance.
I have (quite deliberately) avoided using the formulae that have been developed to analyse the circuit, because for 99% of cases they don't really help. The only thing that's important is to ensure that the resistors are accurate. R1 is always the same value as R3, and R2 is always the same value as R4. The circuit can be configured for gain or attenuation, but is not easily made variable. If you happen to need variable gain, there are far better circuits, which are described elsewhere on the ESP site.
Hopefully, this article has removed some of the doubts you may have had about this simple circuit, and has helped to explain it in a way that makes sense.
 Main Index
Main Index Articles Index
Articles Index