

|
| Elliott Sound Products | Amplifier Basics - How Amps Work (Part 4) |
 Main Index Main Index
 Articles Index Articles Index
|
No discussion of amplifying devices would be complete without a discussion of opamps (aka op. amps). Although not a single device, the opamp is considered to be a building block, just like a valve or any transistor.
The format I used for the other discussions is not appropriate for this topic, so will be changed to suit this most versatile of components. I shall not be covering esoteric or special purpose types, only the basic variety, as there are too many variations to cover.
The operational amplifier was originally used for analogue computers, although at that time they were made using discrete components. Modern (good) opamps are so good, that it is difficult or impossible to achieve results even close with discrete transistors or FETs. However, there are still some instances where opamps are just not suitable, such as when high supply voltages are needed for large voltage swings.
The majority of power amplifiers (whether bipolar or MOSFET) are in fact discrete opamps, with a +ve input and a -ve input. You tend not to see this, but have a look at Figure 3.5 again. The signal is applied to the +ve input at the base of Q1. The base of Q2 is the -ve input, and is used for the feedback signal, exactly the same as you will see in Figure 4.1a below.
Unlike the other devices, opamps are primarily designed as voltage amplifiers, and their versatility comes from their input circuitry. Opamps have two inputs, designated as the non-inverting and inverting (or simply + and -).
When wired into a conventional amplifier circuit, the opamp has one major goal in its little life ...
Make both inputs the same voltageIf, because some swine of a designer has made this impossible (very common with a lot of circuits), the opamp then takes another approach ...
Make the output the same polarity as the most positive inputThe latter condition needs a small explanation. If the +ve input is most positive, then the output will swing to the positive supply rail (or as close as it can get). Should the -ve input be more positive, then the output will swing to the negative supply rail. The difference between the two inputs may be less than 1mV! Simple as that.
I call these "The First and Second Laws of Opamps". These two statements describe everything an opamp does, and just by knowing this, makes the task of working out what most common circuits do a simple process. There is actually nothing especially complex about opamps, unless you look at the 'simplified' circuit diagram often included in data sheets. Don't do this, as it is too depressing. (By the way, the first statement is not strictly true of real-life devices, which will always have some error, however without very specialised equipment you will be unable to measure it.)
Modern opamps (the good ones, anyway) are as close as anyone has ever got to the ideal amplifier. The bandwidth is very wide indeed, with very low distortion (0.00003% for one of the Burr Brown devices), and low noise. Although it is quite possible to obtain an output impedance of far less than 10 Ohms, the current output is usually limited to about +/-20mA or so. Supply voltage of most opamps is limited to a maximum of about +/-18V, although there are some that will take more, and others less.
Depending on the opamp used, gains of 100 with a frequency response up to 100kHz are easily achieved, with noise levels being only very marginally worse that a dedicated discrete design using all the noise reducing tricks known. The circuits shown below have frequency response down to DC, with the upper frequency limit determined by device type and gain.
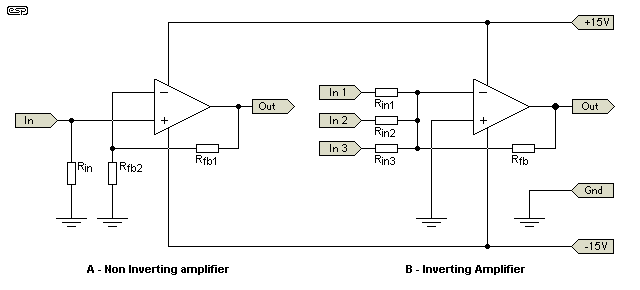
Figure 4.1 shows the two most common opamp amplifier circuits. The first (4.1a) is non-inverting, and is the better connection for minimum noise. The voltage fed back through Rfb1 will cause a voltage to be developed across Rfb2. The output will correct itself until these two voltages are equal at any instant in time. It does not matter if the signal is a sinewave, square wave, or music, the opamp will keep up (provided you stay within its capabilities). Once the speed of the opamp is not significantly higher than the rate of change of the input (generally a factor of 10 is sufficient - i.e. the opamp needs to be 10 times faster than the highest frequency signal it is expected to amplify), the output will become distorted. At voltage gains of 10 or less, almost any opamp will be able to keep up with typical audio signals, but (and be warned) this is no guarantee that they will sound any good.
Input impedance is equal to Rin, and voltage gain (Av) is calculated from ...
Av = (Rfb1 + Rfb2) / Rfb2 or ... Av = Rfb1 / Rfb2 +1
The second circuit (4.1b) is an inverting amplifier, and is commonly used as a 'summing' amplifier - the output is the negative sum of the three (or more) inputs. It is also called a 'virtual earth' mixer, because the -ve input is a virtual earth (remember my 'First law of opamps'). If the +ve input is earthed (grounded), then the opamp must try to keep the -ve input at the same voltage - namely 0V. They are used in many diverse applications, and are common when a signal polarity must be inverted.
It does this by adjusting its output until the current flowing through Rfb is exactly the same (but of the opposite polarity) as the current flowing into the inputs from each Rin. They must all sum to 0V, as they are equal and opposite. This is done with amazing speed, and good opamps will continue to succeed in fulfilling the First Law up to over 100kHz or more (depending on gain). Lesser devices will start to have trouble, and the appearance of a measurable voltage at the -ve input is an indication that the opamp can no longer keep up with the signal.
Input impedance is equal to RinX (where X is the number of the input), and voltage gain is calculated from ...
Av = Rfb / RinX
Multiple inputs can all have different gains (and input impedances). There are two catches to this circuit. The first is that if the source does not have an output impedance significantly lower than Rin, then the gain will be lower than expected. The other, not always realised, is that if the circuit is configured for a gain of 1 (actually it is technically correct to refer to it as -1), Rin1, Rin2 etc. will all be equal to Rfb. If the circuit has 10 inputs, then from the opamp's perspective it has a gain of 10, and its frequency response and noise will reflect this.
There are literally hundreds of different opamp circuit configurations. Feedback circuits with frequency dependent components (capacitors or inductors) make the opamp into a filter, or a phono equaliser, or almost anything else.
For an in-depth look at opamp circuits, see the Designing With Opamps series.
Opamps even come in power versions, using a TO-220 (or other specialised) case, and are typically capable of around 25W to 50W or more into an 8 Ohm speaker load. These devices, while not necessarily considered to be to audiophile standards, are still very capable, and have been used by many domestic appliance manufacturers in such things as high-end TV sets and even 'high end' hi-fi equipment. Some of the more advanced devices are capable of output power up to 80W. It is very doubtful that even the most 'golden eared' reviewer would pick that an amplifier used a monolithic power amp (power opamp) in a double-blind test.
They typically have distortion figures well below 0.1%, and can be used anywhere a small, convenient and cheap power amp is required. The circuit looks almost identical to that of a small signal opamp, except that a Zobel stabilisation network is used on the output to prevent oscillation. There are several circuits amongst the ESP projects, and PCBs are available for the most popular designs.
Previous (Part 3 - FETs) Next (Part 5 - Building Blocks)
 Main Index Main Index
 Articles Index Articles Index
|