

|
| Elliott Sound Products | Project 180 |
Some people like the idea of a VU ('volume unit') or power meter on their power amps. While LED columns are popular, they are very distracting because of comparatively bright LEDs flashing on and off in one's peripheral vision. For example, It's not something I'd ever use on my own system for that reason. A 'true' moving coil meter is far less obtrusive, especially if it's illuminated by LEDs that can be dimmed, which can even be 'automatic', so the light level is dependent on the room lighting. This option means there are no brightly lit meters when one is watching TV for example.
Because moving coil meter movements are available in a wide range of currents for full scale, there will always be some calculations to be made to ensure that full scale on the meter corresponds to full power. In this design, I've elected to use higher value trimpots than I'd normally recommend, as this allows the unit to be set up easily for a wide range of amp power ratings without changing the circuit at all. The maths behind the values are described, although this is optional (but recommended) reading.
Many people consider a meter to be a 'toy', because while it may be calibrated in watts, the meter almost invariably displays only volts. However, if it's done properly (as a peak indicator) it tells you how close you are to your amp's clipping point. This is particularly important if you regularly push the boundaries and listen loud, because a clipping amplifier can place your speakers at risk due to excessive continuous power (this is not because "clipping kills speakers" - it does no such thing in isolation).
If you wanted to measure actual power, then the circuit becomes far more complex, and requires you to use an analogue multiplier or a PIC programmed to compute power. This is rarely a requirement - mostly people want an indication of the level rather than the power. Indeed, it's quite likely that a true power meter will indicate that power is within limits, but the amp is clipping on transients. For this reason, a VU meter's ballistic response (the term used to describe the pointer's rate of change, overshoot, etc.) is less than ideal, and a 'peak programme' response is preferable.
Project 55 is an active design that works well, but sometimes it's easier to just power the meter directly from the power amp's output. This is complicated a little if your amplifier(s) use a BTL (bridge tied load) output, where there is often a constant DC voltage present (referred to ground) with no signal. However, this is easy enough to get around.
This project is as simple as they get at first glance, but there are a number of things you need to get right if the meter is to give a usable display with normal programme material. Since most amps are not operated at anywhere near full power most of the time, it's handy to include a 'high/ low' range switch, with the low range reading full scale at a lower power level. It's up to the constructor to determine this level, based on listening habits.
For the examples shown here, the low range is 1/10th the full output power. So for a 100W/ 8 ohms amp, this indicates a voltage of 28V RMS at full power, or 10W for the low range (about 9V RMS close enough). Peak voltages are 42V and 12.7V respectively. Your amp(s) will almost certainly be different, but the values are all easy to calculate, needing nothing more complex than Ohm's law. With the values provided in Figure 2 you'll find that the trimpots allow adjustment over a very wide range, and should allow most amps to be used with no changes to the circuit at all.
The essentials are shown in Figure 1, and include the mandatory rectifier, and a series resistance that sets the meter current at full power. The series resistance will be a fixed value in series with a trimpot, so the level can be set properly, and the values of each depend on the meter coil's resistance and current for full scale deflection. The 1k resistor in series with the input to the bridge rectifier is there to isolate the non-linear diode current from the amp's output. While the impedance is very low, we don't want to add any distortion to the output by including a non-linear load.
Note that no part of the metering circuit may be connected to earth/ ground. Because a bridge rectifier is used, the circuit must be completely floating, and it's also important to keep amplifier input leads well clear of the metering circuitry. Non-linear current flows in most of the circuit, and you don't want that coupled into the amplifier's inputs as it will cause distortion.
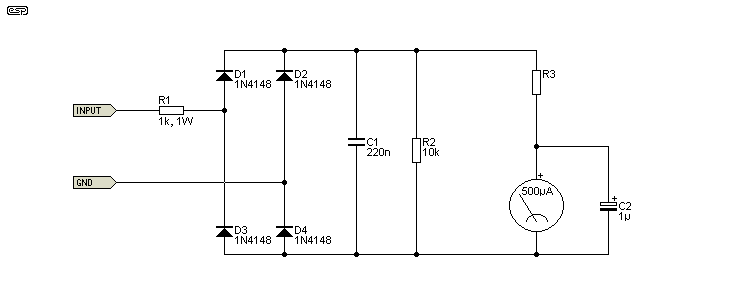
Figure 1 - Meter Circuit Principle (One Channel Shown)
A capacitor (C1) is included to provide the 'peak detection' function. Without that, the meter can only display the (rectified) average current. A second capacitor (C2) damps the meter movement, and this will be necessary with most moving coil movements because very few have the necessary electro-mechanical damping inside the meter. Please bear in mind that some meters will have an internal rectifier, and unless you only want the most basic of displays possible, this must be removed. During the heyday of moving coil meters, they were available with very well defined ballistics, but this time has passed and most are unpredictable.
Those available now are generally very basic indeed, and the ballistics are generally poorly controlled, or are not controlled at all - the pointer will typically show significant overshoot when current is applied, causing the reading to be very hard to determine with music or speech signals. By adding a capacitor of the correct value, the ballistics can usually be controlled well enough to get a sensible reading, even with varying voltages.
The value of R2 has to be selected based on the amplifier's output voltage and the meter's FSD (full scale deflection) sensitivity. This varies widely, ranging from around 50µA up to 1mA (although some may be higher). In general, lower current is preferred because this means higher value resistors (and lower power dissipation), along with lower value capacitors which are smaller and cheaper. For most people, it's far easier to use a trimpot in series with R3, that lets the meter to be 'calibrated' for almost any power amplifier. The circuit below (Figure 2) is based on a 500µA movement with a coil resistance of 650 ohms. This type of meter seems fairly common on a well-known auction site, but there are several others that are likely to be suitable. The selection of C2 is determined empirically (i.e. by observation and experiment), because there's no way to know what the ballistics are like until the meter is tested with a signal.
Because the diodes are not within a feedback loop (which would require an opamp), the reading is not linear at low output levels.
| Input (RMS) | DC (Peak) | Ideal (Peak) | Error (%) | Watts (8Ω) |
| 1V | 264 mV | 1.41 V | 435 | 125m |
| 2V | 1.47 V | 2.83 | 92 | 500m |
| 3V | 2.81 V | 4.24 | 51 | 1,125m |
| 4V | 4.18 V | 5.66 | 35 | 2 |
| 5V | 5.57 V | 7.07 | 27 | 3.125 |
| 6V | 6.95 V | 8.48 | 22 | 4.5 |
| 7V | 8.34 V | 9.90 | 19 | 6.125 |
| 8V | 9.74 | 11.31 | 16 | 8 |
| 9V | 11.13 | 12.73 | 14 | 10.25 |
| 10V | 12.52 | 14.14 | 13 | 12.5 |
| 11V | 13.91 | 15.55 | 12 | 15.125 |
| 12 | 15.30 | 16.97 | 11 | 18 |
| 14 | 18.10 | 19.80 | 10 | 24.5 |
| 16 | 20.89 | 22.62 | 8 | 32 |
| 18 | 23.69 | 25.45 | 7 | 40.5 |
| 20 | 26.51 | 28.28 | 7 | 50 |
The meter should be calibrated with an amplifier output level of the maximum available (before clipping of course), and preferably not less than 20V RMS (amplifier allowing of course). This negates the residual error and means that the higher voltages will be displayed with little error. Although not shown in the table, the error at 50V input is about 3%. The idea of this project is to provide an indication of power, it is not intended to be an accurate indication, because it only measures amplifier voltage, and can't measure actual power. If you need to measure real power, then look at Project 189, which uses an analogue multiplier IC to compute actual power based on voltage and current at any point in time.
The end result is very close to the idealised circuit shown above. The difference is that trimpots are used to allow the levels to be set exactly, and there are two ranges, typically separated by 10dB (a factor of ten). Further below the formulae are provided to let you determine the resistor and pot values if you wish to adapt the circuit to amplifiers of any power. There is also information that describes how to use meters with different sensitivities, typically less than 500µA. Less sensitive meters can also be used, but you'll need to re-calculate the trimpot values (and beware of power dissipation in the trimpots).
As a rough guide, I suggest that the time constant based on the meter's DC resistance and the damping cap (C2) should be around 1ms. For a movement with a DC resistance of 650 ohms, that means a capacitance of around 1.5µF, but anything from 1µF to 2.2µF will probably be alright.
The value of C1 determines how well (or otherwise) the meter will display the peak value. This is the critical one if you want to know if the amp is (close to) clipping. The time constant of the peak hold circuit is determined primarily by C1 and R2, although it is affected by the meter's series resistor for the full power range.
We don't need to worry when the low power range is selected, because the maximum power is only 1/10th of full power. If the meter stays below FSD it's still well away from clipping, so there is no need to ensure that the peak hold capacitor really does maintain the peak for long enough for the meter to respond. The diodes will normally be 1N4148 or similar, but with amplifiers of 500W or more, they should be changed to UF4004 or equivalent high speed diodes. 'Ordinary' power diodes should ideally not be used because they are too slow to respond properly to higher frequencies. However, it's probable that they will be alright because the amplitude of high audio frequencies is generally fairly low.
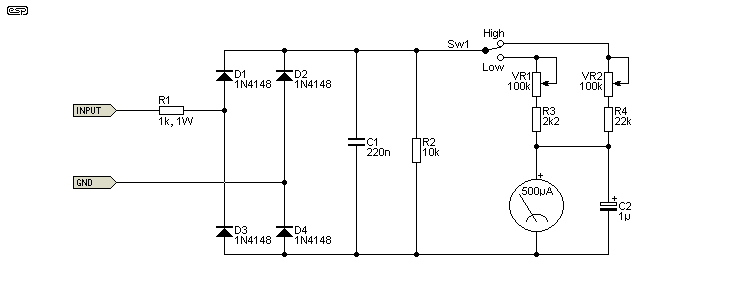
Figure 2 - Complete Meter Circuit (One Channel Shown)
The trimpots are both 100k, which gives a very wide variation for amplifier power, and will also cover a range of different meter sensitivities. I've based the circuit on the use of a 500µA meter, but it's readily adapted for higher or lower sensitivities by changing the values of the trimpots and their series resistors. For example, if the meter has a FSD of 100µA, it will be easier to just stay with the 500µA values, and add a resistor in parallel with the meter movement (a current shunt). This is explained below.
The following table shows the resistor values required to set the power levels for your amplifier(s). As you can see, the trimpots have more than enough range to cover power amplifiers from as low as 3W up to 500W (8 ohms). If your amp is over 500W (why?), then the value of R4 can be increased to allow for a higher input voltage.
| Power (max) | Voltage | 1/10th Power | Voltage | R high | R low |
| 500 W | 63 RMS, 90 peak | 50 W | 20 RMS, 28 peak | 120 k | 37 k |
| 250 W | 45 RMS, 63 peak | 25 W | 14 RMS, 20 peak | 90 k | 25 k |
| 125 W | 32 RMS, 45 peak | 12.5 W | 10 RMS, 14 peak | 39 k | 16 k |
| 65 W | 22 RMS, 32 peak | 6.5 W | 7.2 RMS, 10 peak | 43 k | 10 k |
| 32 W | 16 RMS, 22 peak | 3.2 W | 5.0 RMS, 7 peak | 28 k | 6 k |
The values for R high and R low are approximate, and will give 500µA meter current. If your meter is more sensitive, see below to determine a parallel resistance that gives an overall sensitivity that's the same. This makes it un-necessary to recalculate the values for the trimpots and series resistors. As is obvious, there is more than enough range to accommodate intermediate power levels using the suggested values. Having a low range for a small amplifier (less than ~40W or so) doesn't make much sense, but can be included if you wish. Note that with lower powered amps, C1 should be increased to around 470nF to ensure that the peak voltage is detected reliably.
To some extent, most calculations are redundant because there's so much adjustment range. Still assuming a 500µA meter, the high range can be adjusted for any amplifier between 30W and 500W, with the low range covering 3W up to 250W. Should you decide to add a shunt resistor to a more sensitive meter to reduce it to 500µA, that's easily calculated. As an example, assume a 100µA meter, with s series resistance of 2k (note that there are no hard-and-fast rules regarding sensitivity vs. coil resistance). To pass 100µA through 2k requires a voltage of 200mV (Ohm's law). A parallel shunt resistor therefore must pass 400µA for an overall sensitivity of 500µA.
R = V / I
R = 200mV / 400µA = 500 ohms
So, a 500 ohm resistor in parallel with the 100µA meter now makes the FSD current 400µA total, so everything else remains the same. You only need to know two things, the FSD current for the meter, and its coil resistance. The remainder of the circuit is unchanged, reducing the amount of work needed to determine the series resistors to nothing. In reality, the 500 ohm value is flexible too, so it can be either 470 or 560 ohms, giving slightly less or more sensitivity respectively.
You must know the FSD sensitivity of the meter and its resistance. Be careful if you try to measure coil resistance with an ohmmeter, as many can provide far more current than the meter is designed for. Ideally, use a higher resistance range on multimeters with fixed ranges, but it's harder if the meter you use is auto-ranging. If this is the case, use a 1k resistor in series with the movement's coil to limit the current. The resistance reading then simply requires that you subtract 1k. You might measure 1.65k for example, so the meter has a 650 ohm coil. Having said this, I have always used a multimeter, and while the meter's pointer may pin to the end-stop, I've never damaged one. With the circuit shown, it will suit amplifiers covering quite a wide range of power levels.
Predictably, you will need to calibrate your meter face if you wish to see an approximate representation of the power used at any given time. This can't be done without having the meter and amplifier to hand, so I haven't included a scale here. There is no requirement to use a load on the amplifier unless it has modified output impedance (P27 power amp for example), or uses valves in the output stage. In both cases, the amp's output level still matches the meter calibrations, but valve amps in particular can be damaged or misbehave with no output load.
For something like this, the maths behind it are not necessary, but there will be some readers who want to know how to do their own calculations. While not essential, you learn a lot more about the workings of any electronic circuit by running your own calculations to see just how the values shown came about. This is my recommendation with any circuit, as it's the only way you get to understand electronics properly.
For the sake of this exercise, we'll use a 100W/ 8 ohm amplifier as an example. All calculations can be used for any power level, and it's simply a matter of knowing the actual power output of the amp into a given impedance. Relying on hearsay or what you think the amp can do is ill advised, and you may need to measure the output at the onset of clipping to get the real figure. We aren't interested in the power output as such, only the output voltage. Note that if you use a digital multimeter to measure the voltage, I suggest a maximum frequency of 100Hz, because most do not respond well to high frequencies. Alternatively, just measure the supply voltages, subtract around 5%, and use that as the peak output voltage.
VOUT = √( Powerout × Znom ) (Where Znom is the nominal speaker impedance)
A 100W/ 8 ohm amp will deliver 28V RMS at full power, and 9V RMS at 1/10th power (10W). The peak amplitude is worked out easily ...
Vpeak = VRMS × √2
Vpeak = VRMS × 1.414
For our demonstration amplifier, the peak voltages work out to be 40V (full power) and 12.7V (1/10th power). We can ignore the diode voltage drops, because influence of R1 (1k) makes the small voltage drop irrelevant. The calibration trimpots are designed to have enough range to set the meter accurately, despite 'errors' created by the input resistor. There is a voltage divider created by R1 and R2 (as well as the meter circuit itself), and this can't be ignored. With the values shown, the 'ideal' peak voltages are reduced to 36V and 11.5V (high and low ranges respectively). Because the low range uses a comparatively low feed resistor (at least for our 500µA demonstration meter movement), the signal is attenuated a bit further, and will actually be an average of around 7.5V after the rectifier.
You may well wonder why the voltages are so much lower than they should be. The answer lies in the 1k input resistor. It is included to ensure that the amp's output isn't subjected to excessive distortion caused by the non-linear behaviour of the diodes. The peak voltage across R1 is much higher than the voltage worked out by simply including R1 and R2 (in parallel with the meter multiplier resistor) as a voltage divider, so the output voltage is lower. The main issue is that the voltage dropped across R1 is not determined by any immediately apparent linear function, due to the presence of C1. Without C1, the meter will display the average voltage, and that won't be as helpful because clipping can't be detected with an average-responding meter.
While it's certainly possible to calculate all voltages accurately, a generalised figure of about 1.4 will get you close (i.e. V peak / 1.4). Overall, it's simpler to use trimpots that have enough range to cover all contingencies. The low range uses a 2.2k resistor and another 100k trimpot. There's absolutely no reason to have such a high value, but it means that only one trimpot value is needed for all locations. Worst-case power dissipation in the high-range trimpot (with a 500W amp) is about 30mW, well within the ratings of most available parts. Dissipation is lower for the low range because the voltage is reduced.
The total resistance needed for 500µA with 7.5V is (from Ohm's law) 15k. With the full 40V input, the DC voltage across C1 will be around 27V (this is from a simulation of the circuit). The resistance required is therefore 54k. Since the meter's coil resistance is 650 ohms it can be ignored, as the trimpots can easily compensate. When the low range is selected, it's easier to switch between separate resistor networks, because that makes it easier to work out the required values.
If the meters you use are less sensitive (e.g. 1mA), then the trimpot and series resistor values must be reduced, but beware of power dissipation, particularly in the trimpots. For example, if you had a 500W amp and reduce the trimpot to 50k, dissipation will be around 65mW which may stress the trimpot (most are not designed for dissipation greater than around 100mW, some are less). This is something you must verify for the pots you intend to use. Most pots and trimpots are actually limited to a particular current, so a 100k, 100mW pot has a maximum current at any setting of 1mA ...
P = I² × R ) therefore ...
I = √( P / R )
None of this is difficult, but it does require that you think about the circuit interactions and understand Ohm's law. For anyone who wants to know more about meter multipliers (series resistors) and shunts (parallel resistors), I suggest that you read the ESP article Meters, Multipliers & Shunts for the background information. The article concentrates mainly on DC applications, but it will improve your understanding the concepts used in this project.
This is a simple circuit, and it doesn't use (or need) any opamps or transistors. It will give you a reasonable indication of the power amplifier's peak output voltage (it does not and cannot display 'Watts'), so you know if you are close to clipping the amp's output. The overall response time will typically be around 2ms, but this depends on the meter used. Since most amplifier power is concentrated on low to medium frequencies (from 40Hz up to 500Hz or so), it will respond well to the audio input signal.
The ballistics of the meter you use will determine how much overshoot you see. This is highly variable, and it's very difficult to know in advance if your meter will be acceptable or not. For meters that show considerable overshoot, C1 should be increased until the display looks acceptable. The idea of this project is to give you a general idea of power levels, and it is not intended to be a precision indicator.
Many people consider a 'power meter' to be simple bling - it looks nice, but serves little or no real purpose. This isn't necessarily true, but you must understand exactly what it does and its limitations. If calibrated well (and meter ballistics are controlled), it still looks 'nice', but it does show you if the amp is close to (or beyond) clipping. If any amp is pushed hard enough to develop partial clipping, the average voltage is increased and the meter will be 'pinned' to the end-stop for much of the time. If you can't hear that the amp is clipping, the meter will show you.
Use is not strictly limited to transistor amplifiers, but be warned that some valve (vacuum tube) amps have a relatively high output impedance, and the diode rectifiers may introduce audible 'artifacts' that will not sound pleasant. If your valve amp doesn't have an output impedance of less than 0.5 ohm, I suggest that you use an active design, such as Project 55 which doesn't place a non-linear load on the amp's output.
I've not included any details of the meter face, because that can differ widely depending on the unit you get. Some are 'calibrated' in dB, with a typical maximum of +3dB. If your meter is like that, then I'd set it so that +3dB (full scale) corresponds to full amp power, and if you ensure that the pointer remains at or below the 0dB mark, the amp retains some headroom and is unlikely to clip, even on transients. This is achieved because of the peak detection used in this project (C1).
Note that there is no circuit shown here for meter illumination. Some meters have integral LEDs that light up the dial (usually far too brightly), but this is easily fixed by selecting the resistor values in series with each LED. Other meters may use incandescent lamps for illumination (especially older or 'new old stock' meters), and some have no provision at all. I mentioned an 'automatic' lighting control in the introduction, but unless there is sufficient interest I'm not going to experiment with a suitable circuit. It may be possible just with an LDR (light dependent resistor) wired in series with high brightness LEDs, so when the room lights are on the LEDs come on quite brightly, and when off, the level is reduced accordingly. A predictable (or 'pre-settable') illumination system will require a suitable DC power supply, LDR, trimpot(s) and probably a transistor if the LDR is unable to supply enough current by itself (which is likely).
 Main Index
Main Index
 Projects Index
Projects Index