
 |
| Elliott Sound Products | Passive Line Level Crossovers (PLLXO) |
 Main Index
Main Index Articles Index
Articles Index For reasons that are unclear to me, some people seem to imagine that all circuitry should be passive. This is clearly not possible for power amplifiers, and presumably they will have to be blessed, then coated liberally with fairy dust (more commonly known as snake oil) so as not to affect 'the sound'. The notion that a passive line-level crossover (PLLXO) must be 'better' (no horrible opamps for example) is wishful thinking, and doesn't stand up to scrutiny. Remember that the vast majority of all recordings have had individual tracks and the final mix pass through more opamps than will ever be found in a home reproduction system. It seems that this point is missed, or perhaps it 'doesn't count' for some reason.
The answer to the question posted in the title ('Useful Or Not?') is 'not'. Basically the whole idea is based on a false premise, and the performance can never reach that of a properly designed active crossover network. While this can be mitigated by using an opamp buffer before and after the passive network to ensure a low source impedance and a high (approaching infinite) load impedance, this means that it's not 'passive' any more. Using 'simpler' circuits (valve cathode followers, FET source followers or transistor emitter followers) will increase distortion and most will fail to approach the performance of an opamp by an order of magnitude.
A crossover network is always a requirement with any system using two or more loudspeaker drivers. The choice of frequency (or frequencies for multi-way systems) depends on the drivers used, and the slope depends on personal preference, driver protection and the level of complexity the constructor is willing to undertake. While some high quality systems go to great lengths to get everything right, many don't, so the result is not always as expected (or hoped for). The vast majority of loudspeakers have an internal crossover network, ideally using inductors, capacitors and resistors, but on occasion just a single bipolar electrolytic cap may be used (this is not a crossover - it's a cheap (and very dodgy) way to 'protect' the tweeter).
The idea that passive 'line level' (as opposed to speaker level) systems avoid the use of opamps, bipolar transistors, FETs or valves (vacuum tubes) seems to be appealing to some DIY people, but consider that no major manufacturer will attempt to use a completely passive system because it imposes too many restrictions. Snake-oil vendors are not included of course, because they are selling dreams rather than reality. You must 'believe', or the magic will dissipate and reality may even become apparent. That would never do!
My preference is for 'proper' active crossovers, but for a simple system this may be thought difficult to justify. The cost penalty isn't great, but it adds a few more parts. However, these extra parts also ensure that it works correctly, and doesn't rely on the vagaries of the external components (preamp and power amp). All 'line level' crossovers mean that a four-wire (or more) connection is needed for the speaker. This usually isn't sensible for a simple 2-way box that is used at low power, and often a simple 2-way series speaker level crossover is all you need. An example of just such a system is shown in Project 73 (Hi-Fi PC Speaker System), and that shows a series network. This has been in daily use for nineteen years (at the time of publication of this article), and has seen several different PCs in its time. Apart from one repair (a faulty electrolytic capacitor in the power supply), the system hasn't missed a beat in all that time!
For the time being, we'll imagine that a PLLXO is (potentially) viable, and look at the limiting factors. These are always present with any system, but fully passive filters are far more easily compromised than an equivalent active system. The more compromises you have to make, the greater the performance degradation.
If you want to bi-amp using a passive crossover then there's really no need to make it complex unless you are after something that has greater than 6dB/ octave slope (as discussed in this article). However, to be useful the network requires a sufficiently low output impedance to ensure that it isn't loaded by the following power amplifier. Any loading will not only alter the crossover frequencies, but also create response errors. If the passive network is loaded by an impedance that's ten times the nominal filter impedance, the frequency shift is minimal, but there will be a level difference of 0.8dB between the high and low pass sections. A pair of simple networks are shown below, with a nominal crossover frequency of 3.38kHz. It's not recommended, and it's shown only to demonstrate the principle.
First, it's necessary to determine the optimum crossover frequency. The frequency is determined by the following formula ...
fo = 1 / ( 2π × R × C ) Where fo is the desired XO frequency
Armed with this, the networks can be designed. The drawing below shows both first (6dB/ octave) and second (12dB/ octave) filters. With an infinite load impedance (or close to it), the 6dB/ octave filter will sum flat to within well under 0.01dB - a perfect result. However, an infinite load impedance isn't possible, so it will have to be something finite (which is most inconvenient).
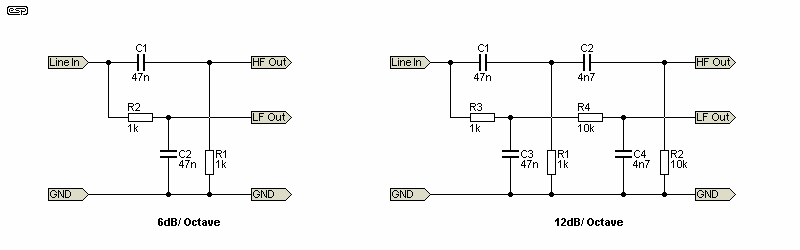
Figure 1 - First & Second Order PLLXO, 1k Impedance, 3.38kHz Crossover Frequency
It's an absolute requirement that the source impedance should be no more than a few ohms, or the crossover frequency will be affected, as will be the relative levels between high and low pass filters. The minimum impedance for all networks is close to 1k, with an impedance at the crossover frequency of 1.414kΩ This isn't an easy load for most preamps, and is completely unrealistic for a passive preamp. This is doubly true if the 'passive preamp' has only a volume pot, or uses a transformer to get gain. It's even a difficult load for some opamps. The impedance of the following power amplifiers has to be at least 100kΩ to prevent level variations. It should be apparent that this isn't a viable option for the vast majority of systems.
If you'd prefer a 12dB/ octave filter then you are in for a world of pain. It can be done as shown above, and the filters still need a very low source impedance. The required load impedance now needs to be around ten times higher than before, so you need power amps with a 1MΩ input impedance, and there will be a 0.5dB dip at the crossover frequency. You also have to reverse the phase of one driver to prevent having a deep notch at the crossover frequency (all second-order crossover networks require a polarity reversal).
Provided you know the exact input impedance of the power amplifiers you are using, this can be used as part of the filter network. While this works with high-pass filters, it's not ideal for the low-pass section. The amp's input impedance is in parallel with a capacitor but in series with the low-pass resistor, and that reduces the level of the low frequency section. If the power amps have gain controls this can be addressed, but the input impedance (and therefore the gain control) still needs to be at least 100k to 1MΩ. With a 100k load, the 12dB/ octave filter will have the response shown below.
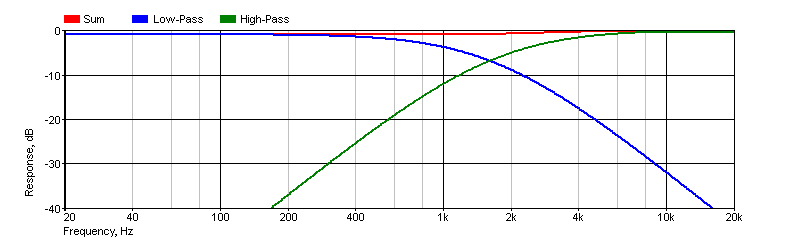
Figure 2 - Second Order PLLXO Frequency Response
I don't know who originally thought that a PLLXO was a good idea, but in a nutshell, it's not. Certainly, some of the issues can be addressed using capacitors and inductors, but then you have a system that still needs a low source impedance, but it also needs high-value inductors, and a well defined and unchanging load impedance. If it's imagined that this is somehow 'better' than a proper active filter using opamps, then be prepared to be surprised (but not in a good way).
There is one (very small) benefit, in that you now have a line level crossover that uses separate power amps for each driver, so there is no need to be concerned about driver impedances. However, a proper active crossover will outperform it in every way. The idea that opamps somehow 'ruin' the sound is just silly, and an active crossover is a far better (and more predictable) option overall. The circuits shown here are examples only, and I don't propose to discuss the design process in any more detail. Any circuit that is so dependent on external influences (in this case, output and input impedances) is not especially useful unless it's incorporated within the main chassis and doesn't rely on any external equipment.
If you are game enough, you can use capacitors and inductors to realise the filter function required. There's one small problem that I have covered before, namely that inductors are the worst passive components you can buy. Because they rely on magnetics, they are very susceptible to stray magnetic fields, their internal resistance is often rather high, and they suffer from 'self resonance' due to the distributed capacitance within the windings.
However, I'll persevere because you can buy line-level crossovers that use them. The requirements as described above do not change, so the source impedance must be low (ideally very low) and the filter characteristics are affected by the load impedance (the power amplifiers). R1 and R2 in both versions provide the correct terminating impedance for the filters, and if the amplifier's input impedance is less than ten times the resistor value, response will be seriously affected. There's another small trap waiting for you as well, namely the resistance of the inductors. They are comparatively high values, and will require many turns of fine wire and a ferrite magnetic path. Air-cored inductors would be impossibly large, and very susceptible to magnetic interference. The 12dB/ octave filter is aligned for a Q of 0.5 (Linkwitz-Riley), so the outputs will sum flat.
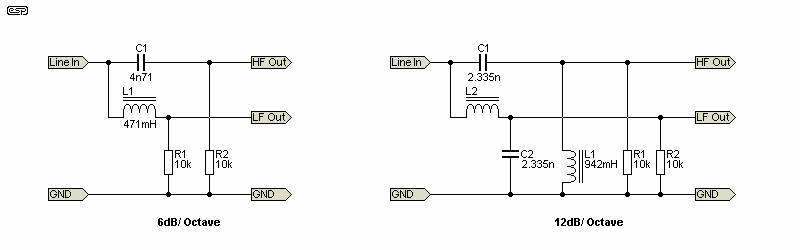
Figure 3 - First & Second Order L/C Filters
In both examples, an amplifier input impedance of 1MΩ will cause a dip of 0.085dB at the crossover frequency. This is reduced if the impedance is higher, and is made worse if the impedance is lower. The amplifier's input impedance can be made a part of the circuit. For example, an amp with an input impedance of 22k (very common, and used in most ESP designs), then R1 and R2 can be increased to 18.33k. That provides almost exactly 10k load to the filters and they will be close to perfect (or as 'perfect' as can be achieved with inductors). In reality, there will be response anomalies cause by the winding resistance of the inductors, and adjustments will be necessary to suit the inductors you use.
Calculating the values isn't difficult. The standard formulae are used for both the capacitor(s) and inductor(s), and for the second order filter the Q must be accounted for. The Q for a second order Linkwitz-Riley filter is 0.5, so if RL is 10k and we use the same crossover frequency (3.38kHz) ...
XL = XC = RL / Q Where XL is inductive reactance, XC is capacitive reactance and RL is load impedance L = 2 × RL / ( 2π × fo ) C = 1 / ( 2 × RL × π × fo )
For the 6dB/ octave filter, the Q is always 0.5, and the values of L and C are based on the actual resistance (10k). The value of 2 × RL is only necessary for the 12dB/ octave version. Basically the same formulae are used for speaker crossovers, except the impedance are far lower, meaning higher capacitance and lower inductance. Should you prefer a Butterworth response, you divide the load resistance by 0.707 ( 1 / √2 ). Remember that one output of the 12dB/ octave filter must have its phase inverted - it makes no difference whether it's active or passive, this is required!
It's always a good idea to work any calculated values backwards to double-check your results. If you do this with the values shown in Figure 3, you can re-calculate the frequency and Q of the second order filter. This is also useful to check a circuit you find elsewhere. The formulae you need are as follows ...
fo = 1 / ( 2π × √( L × C )) Where fo is the crossover frequency Q = R / √( L / C )
Quite clearly, the values can be somewhat 'inconvenient' (no standard values), so you can either change the crossover frequency or you'll need capacitors in parallel to get the desired value. The inductors values are also inconvenient, but they will be custom-made so can be made to provide the exact inductance required. Be aware that ferrite pot-cores saturate easily, so you'll almost certainly need to use a core that's larger than expected. If you expect to use a 'line level' voltage of more than 1V RMS, saturation becomes more likely. I do not intend to go through any of the coil design processes, because it would just be a waste of my time. The idea of a passive L/C line-level filter is (IMO) extremely silly, and it deserves no more attention than already provided.
For anyone who still thinks this is a 'good idea', you are now on your own. The end result will be irksome to build, sensitive to magnetic fields, more expensive than an opamp filter, and it won't work as well. Admittedly, you don't need a power supply, but you do need a preamp with low output impedance, or the filters have to be designed with the actual output impedance as part of the design process. I'm not going there.
A rational approach needs active components. There are examples of second-order (12dB/ octave), third-order (18dB/ octave) and fourth-order (24dB/ octave) filters shown in the projects pages, and there's even a state-variable first-order filter. Because it's part of another project (and is also described in the State Variable Filters article), it's included here because it's a far better proposition than a completely passive design. The first-order state-variable filter is uncommon, and this is one of the few websites that describes it.
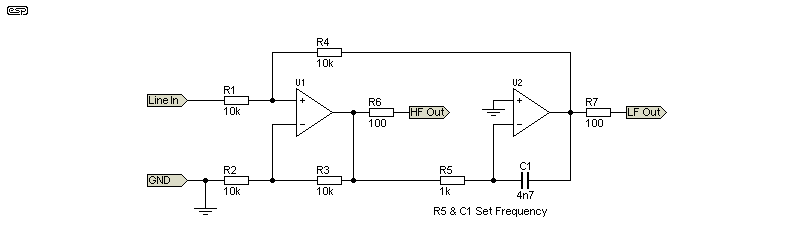
Figure 4 - First Order State Variable Crossover
There's no point showing the response graph because it's perfect! The two outputs combined sum flat, and the frequency has been set to 3.38kHz as before. The frequency can be made variable by using a pot in place of R5, allowing the frequency to be changed at will. There should be a resistor in series with the pot to ensure that the frequency can't be adjusted to anything too high to be useful. Compared to a passive version, the circuit shown doesn't care about the input impedances of your amplifiers, although it does require a low source impedance (in common with just about every filter circuit known).
As with any other circuit using opamps, 100Ω resistors (R6 and R7) are required in series with the outputs if the circuit will be connected to the power amps via shielded cables of more than 100mm or so. These prevent the opamps from oscillating due to cable capacitance. Figure 3 is a real circuit, without compromises, and doesn't require any silly formulae to allow for the input impedance of the power amps. It uses only a single-gang pot (if you need it to be variable), and a dual-gang pot can be used for stereo.
For other slopes (12, 18 and 24dB/ octave) refer to the Project list, as there are examples of each. The 'gold standard' is probably Project 09, which is 24dB/ octave and as close to ideal as you can get. Ultimately, no passive crossover (line level or otherwise) can match the precision and freedom from outside influences as one built properly, using opamps. The passionate hatred of opamps in some circles is baffling, as there are many that come so close to the 'straight wire with gain' ideal that it's hard to even measure their distortion. With a bandwidth from DC to well above the audio spectrum, very low noise and low power consumption (typically less than 5mA for each opamp), it's hard to find any fault with them.
Be that as it may, there are countless websites that will 'explain' how opamps will ruin the sound, and often offer seriously degraded performance alternatives that can never come close to that available from the 'evil' opamp. This has been going on for years, and the PLLXO is just one example of a 'cure' that's far worse than the alleged 'disease'. For those who think that a discrete opamp (using transistors, FETs and other 'conventional' components) is superior to the integrated circuits we use in so many products, you can spend a small fortune to get something that might come close to the common NE5532 opamp, but many times the size. I cannot understand the 'logic' of this.
It's probably due to lack of knowledge of filter principles in general that ensures there will be people who imagine that passive filters of the types described have 'better' phase response than active filters. Especially those using 'nasty' opamps! This is simply untrue. Any filter with a particular slope and/ or Q has the same phase shift as any other, and it makes zero difference if it's active or passive. As noted in the introduction, the music you listen to has almost invariably passed through possibly hundreds of opamp stages during the recording and mixdown processes. More will be used in a disc cutting lathe (for vinyl), and CD players also use opamps as part of the DAC (digital to analogue converter) and to buffer the outputs for low impedance.
There may be a few 78 RPM discs that were cut directly from the studio feed and perhaps only used a couple of valves in the process, but to imagine that these are somehow 'high fidelity' is clearly preposterous. Passive filters were pretty much all that was available in the early days of recordings, but to think that they are superior to a modern version is wishful thinking.
In many cases, when a user tries something different (such as a PLLXO) in place of a more conventional filter, the result may be different. Unfortunately, for many people 'different' means 'better', so myths are created and others come to the same conclusions. Whether this is due to peer pressure, a feeling of wanting to 'fit in' or simple delusion is impossible to know. In most cases, there will never be even the most rudimentary attempt at a blind test, so the results are unreliable at best, useless at worst. Blind testing is the only way to determine if there's a real difference, but it does not provide a means of knowing which is better. That relies on careful measurements, but 'perfection' is not everyone's goal. Ultimately, if you find the sound of a PLLXO somehow 'pleasing', then by all means use it. Telling others that it's better than the alternatives is an opinion, and as such it generally should be treated with some suspicion.
A hundred years ago, these passive filters started to be used in earnest, for telecommunications systems, early radio (wireless) and a few emerging industrial applications. Back then, this was all that was available, so quite naturally they used what they had. Today we can make filters that are closer to the 'ideal' than ever before, and regression to techniques used a century ago is not sensible.
It's no accident or omission on my part that I'm not offering a spreadsheet to calculate the values needed for any given topology. Since the PLLXO is a flawed concept at best, spending more time to develop a spreadsheet isn't worth the time or effort.
 Main Index
Main Index Articles Index
Articles Index