
 |
| Elliott Sound Products | Phase Shift Delay Networks |
 Main Index
Main Index Articles Index
Articles IndexGiven that analogue systems (by definition) use analogue processes, it's an interesting exercise to look at the arrangements we can use to achieve time delays using only analogue circuitry. It's easily added if there's a DSP (digital signal processor) in there somewhere, but the ICs that used to be available to give short delays (generally less than 500µs) have disappeared, so we need to see how it can be done. The traditional method has always been an all-pass filter, which doesn't affect amplitude, but does affect phase. More importantly, they can be used to add group delay, which is what we're after.
Group delay refers to a process where a group of frequencies (a frequency range) is delayed by a predetermined amount, almost always to account for a tweeter being closer to the listener than the midrange driver. To be exact, it's not the diaphragm or the voicecoil, but the 'acoustic centre', which is a lot harder to pin down accurately. Mostly it will require measurement, since (for reasons that I've never understood) this information is lacking in every loudspeaker driver datasheet I've seen.
This omission is a real pain, because measuring the acoustic centre of a driver isn't a simple task. It can be estimated using a number of 'rules of thumb', but ultimately it comes down to measurement [ 1 ]. How you do that depends on what equipment you have available. As a first approximation, the acoustic centre of a driver can be considered the point where the cone is attached to the voicecoil, but there will be differences when it's measured. I've tried for some time to come up with a simple, foolproof method, but thus far without success.
For the examples shown here, the difference between acoustic centres is 25mm, which amounts to a time delay of 73µs (based on the velocity of sound being 343m/s). This changes with temperature and humidity, and you only need to settle on a suitable average value. The phase shift network used to create the delay can be second, third or fourth order, meaning that each section needs to provide a group delay of 36.5µs, 24.3µs or 18.25µs. Don't worry if this doesn't make sense just yet - all will be revealed as we progress.
When designing delay networks, attempting 'perfection' isn't helpful, as a variation of 10% either way usually makes little difference. The acoustic centre of a driver is not necessarily the same for all frequencies, and most of the time a small variation is of no consequence. Few drivers can maintain a response within ±2dB across their range, and if the delay network can keep the theoretical response within that range then that will generally be acceptable.
This article is essentially an addendum to Phase, Time and Distortion in Loudspeakers, which was written way back in 2001. It's taken me a while to provide the essential details, which are only hinted at in the original. However, the two articles are complementary, as this fills in the blanks in the original, and that provides background information in more detail.

Please note that in all the circuits shown here, I have not included a 100Ω resistor in the final output. This is required to prevent opamp oscillation when connected to coaxial cables, which (like all cables) have inductance and capacitance. This often causes opamps to oscillate, and especially if they have wide bandwidth. If you use any of these circuits, the resistor must be included on the output of the final opamp. Likewise, power supplies and opamp bypass capacitors haven't been included either. As should be apparent, the opamps won't work without power, and will oscillate without bypass caps.
To see how driver misalignment occurs, the drawing below shows an example. The precise location of the acoustic centres of the drivers depends on their construction, and their behaviour is not always predictable. It can vary with frequency, and the only way to determine if there is a problem or not is by measurement. One technique is to use an offset baffle, so the tweeter is mounted further back than the midrange. This can work, but it makes the cabinet harder to build and means there's a greater vertical distance between the drivers. The 'stepped' baffle can also create response problems due to diffraction. Some designers use a sloped baffle, but that means that you are listening off-axis.

Figure 0.1 - Driver Offset Causing Tweeter Signal Delay
A flat baffle means that the tweeter is mounted further forward than the midrange driver, so its sound will almost certainly arrive at the listening position first. In this article I've assumed a distance of 25mm between the acoustic centres, but this is only an example. A great deal depends on the drivers themselves, with some tweeters having a relatively deep recess (a partial waveguide), and others less so. Likewise, some midrange drivers are fairly shallow, while others are much deeper. As noted above, it would be helpful if driver manufacturers provided data on the acoustic centre, but they don't.
It's usually obvious with most drivers that the voicecoils will not be aligned. The voicecoil gap is not a reliable indicator of the acoustic centre, but knowing that they are misaligned is usually a pretty good indicator that some remedial action may be needed. Just how much depends on the crossover network and the response deviations of the drivers themselves. There's probably little point trying to correct a 2dB dip (due to delay) if the midrange driver has +2dB peak at the crossover frequency.
All crossover networks have group delay, but it's the same for the high and low pass sections, assuming symmetrical slopes. This applies whether the crossover is active or passive, as it's a simple function of physics. The problem of 'time-alignment' becomes apparent when the acoustic centres of the midrange and tweeter drives are not at the same distance from the listener, and this is almost always the case. It's also highly driver-dependent, as some drivers have their acoustic centre further forwards (or backwards) than others. As noted above, accurate determination of the acoustic centre is not trivial, and it's not a simple 'fixed position', as it can change with frequency.
The effects of a time offset become worse as the filter order is reduced. This is almost certainly the opposite of what you would have thought, but the graphs below show the reality. These are all done using electrical summing, which is the worst case - acoustical summing is never quite as dramatic, but the general trend is the same. I ran simulations with 6, 12 and 24dB/ octave filters, all with the same crossover frequency (2.5kHz) and with an appropriate (phase shift network derived) delay (25mm or 73µs) applied to the midrange. The tweeter delay has to be greater than calculated for the 6dB and 12dB crossovers, because they have more overlap across the crossover frequency range. If the delay extended to the full 20kHz with zero 'droop' there would be no need to extend it, but phase shift delay circuits have an upper frequency limit.
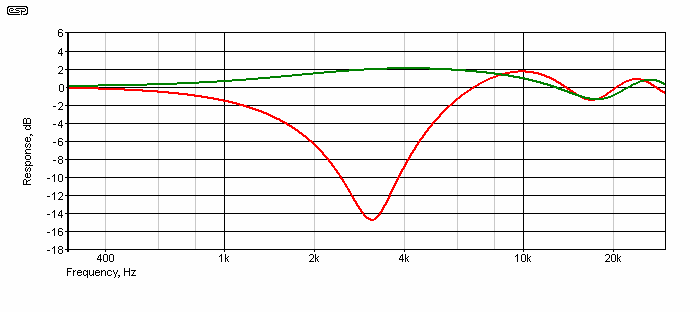
Figure 1.1 - 6dB/ Octave Crossover
In each case, the red trace shows the uncorrected response, with no delay. The delay is set for slightly different periods to obtain improved response with the two lower-order crossovers. For example, with the 6dB crossover, the delay needed to be increased to 108µs to get the response shown, and it could still use some work. Still, the maximum deviation is reduced to ±2dB, and few drivers will match that. However, it would be rather pointless to build an active 6dB/ octave crossover network because not many drivers will perform well, other than at low levels (less than 20W or so), and it's easier to use a simple series passive network. See 6dB/ Octave Passive Crossovers for the details.
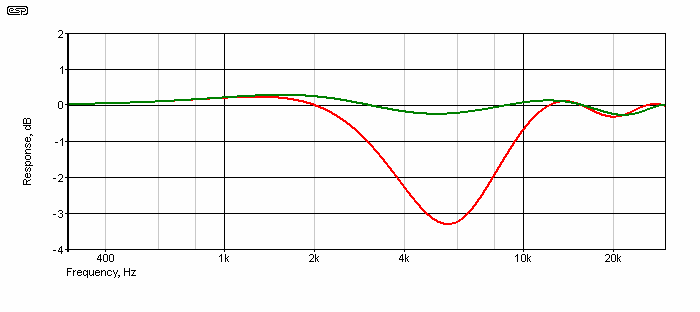
Figure 1.2 - 12dB/ Octave Crossover
This same delay was also used for the 12dB crossover, giving a far more respectable result than using 73µs. The 'wobbles' in the corrected response are no greater than 0.25dB at their worst, and that will be better than most drivers can manage across their passband. When cabinet and speaker surround diffraction are included, the result will almost certainly be a great deal worse. Overall, this is not a bad compromise for people who (for whatever reason) don't like higher order crossover networks.
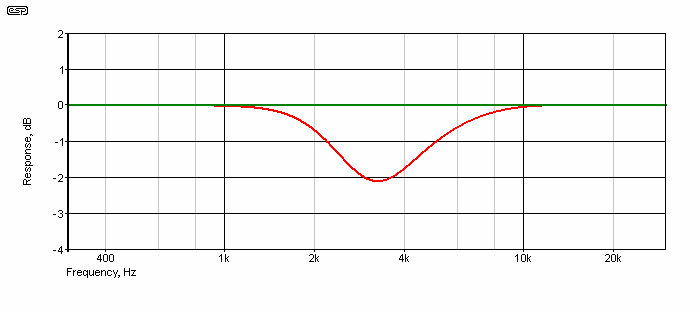
Figure 1.3 - 24dB/ Octave Crossover
With the 24dB crossover, the delay was set for the expected 73µs, and the result is as close to perfect as you'll get. Given that this is electrical summing, there will be other obstacles to obtaining anything near as good when the driver response and diffraction effects are considered. As seen in Figure 1.3, a 73µs delay between the midrange and tweeter causes a dip of just over 2dB, that will (probably) be audible, but other factors may cause response to be affected.
There are many attempts to optimise crossover networks, and some people believe that asymmetrical crossovers are 'better'. While it is possible to arrange for the group delay of each section to be different (typically delaying the tweeter output), at the crossover frequency, even a perfectly aligned asymmetrical network has almost no differential group delay. If you thought that this was a way to create an acoustic offset, mostly you'd be mistaken.
There is never a requirement to apply any correction between the woofer and midrange in a 3-way system. Because the frequency is much lower (my preference is for no higher than 300Hz), the wavelength is such that even a comparatively large offset will have little effect. For example, with a crossover at 250Hz, even an offset of 100mm (291µs) causes a dip of only 0.32dB. This will never be audible as driver response will always have deviations far greater than that. It will cause more issues at higher frequencies, but it will rarely be audible even under ideal listening conditions. 100mm of offset would be unusually high, unless the woofer is particularly large.
Siegfried Linkwitz claimed that "active crossover circuits that do not include phase correction circuitry are only marginally useable" [ 2 ]. Personally, I disagree, for the simple reason that the effects (particularly with a 24dB/ octave filter) are likely to still give a far better result overall than a carefully engineered passive crossover. The latter are notoriously difficult to get right if you aim for 24dB/ octave, and the component sensitivity is high. The 'components' include the drivers themselves, because the voicecoils will change resistance with temperature, and it's almost impossible to correct for that.
Mostly, a good active crossover will beat almost any passive competitor hands down. Adding delay only makes it better, but even without it the results are almost always better than even the most carefully designed passive design. It's pretty much guaranteed that the vast majority of listeners would never pick at 2dB dip at 3.2kHz in anything other than an anechoic chamber, and most wouldn't hear it even there. Small dips are generally considered 'benign', in that they rarely detract from any programme material.
If the midrange and tweeter are not vertically aligned, you'll have issues with directionality at the crossover frequency. The effective combined wave front will move horizontally (or diagonally) us the signal passes through the crossover region. It used to be common to see drivers mounted with horizontal displacement, but few designers will to that any more (other than in 'cheap and cheerful' systems). Predictably, these are not the topic here.
If one driver is closer to the listener than another, the sound from the second driver is delayed. It would be foolish to do so, but imagine that the midrange driver is 1m back from the tweeter. The sound from the midrange driver will reach you 2.9ms later than that from the tweeter, and this will be very audible. In all designs, the actual delay will be much less, and it's based on the acoustic centres of the drivers and their physical position on the baffle. The determining factor is the velocity/ speed of sound in air, taken to be between 343 and 345 metres/ second. Small variations due to air temperature can be ignored because the changes are very small, and attempting to compensate would not be worth the effort.
Many designs use stepped baffles to align the acoustic centres of the drivers, but this comes with caveats. A stepped baffle may create diffraction that can make the cure worse than the disease. The alternative is to delay the output from the tweeter, so that the signals arrive at the listening position with exactly equal delays. This is only important at higher frequencies, where the wavelength is short enough to make the delay cause audible problems. This obviously requires some maths.
λ = c / f (Where λ is wavelength (metres), c is velocity in m/s, and f is frequency)
From the above, it's obvious that the wavelength at 343Hz is one metre, and at 3,430Hz the wavelength is 100mm. Wavelengths are generally considered 'significant' for a ¼ wavelength, or 25mm. If a midrange and tweeter are separated by 25mm or more horizontally (the tweeter's acoustic centre in front of that for the midrange), this qualifies as significant at 3.43kHz. In reality, there will be audible issues at lower frequencies, and for the sake of the exercise here I'm going to assume a crossover frequency of 2.5kHz (24dB/ octave, Linkwitz Riley).
Calculating the delay for a given distance is essentially a rearrangement of the formula for wavelength. Since sound travels at 343m/s, it stands to reason that it will travel 1 metre in 2.9ms. From this we can use the following formula to determine how long it takes for sound to travel the distance between the midrange and tweeter.
Delay = 1 / ( c / distance )
If the acoustic centres are offset by 25mm, the delay is therefore 72.88µs (73µs is close enough). If the acoustic centre offset is (say) 35mm, the delay becomes 96µs. While there are differences caused by temperature, they are insignificant for these calculations. In case you were wondering, no, I will not include formulae using feet, furlongs or fortnights  .
.
The ideal delay is (naturally enough) a real delay-line, but apart from a few (reasonably) high-resolution digital delay ICs that used to be available, this was never really feasible. Even the ones you could get had limited fidelity, but there are no suitable (single IC) devices available any more. Many people have used DSP (digital signal processing) to create both the crossover network and the delay, but there are quite a few who have since purchased Project 09 PCBs and gone back to analogue, because they were not entirely happy with the results. There's no doubt that very good results can be obtained, but you have to pay serious money to get true hi-fi performance.
Converting phase to delay at any given frequency (and vice versa) isn't difficult. The formulae below are for a specific frequency, but for time-alignment we need group delay ...
Delay = Phase° / f / 360
Phase = 360 × Delay × f
For example, a phase shift of 90° at 2.5kHz provides a delay of 100µs, and a delay of 250µs at 2.5kHz requires a phase shift of 225°. These two formulae are useful, but not when designing all-pass filters intended to time-align loudspeaker drivers. They are included for reference, and are very handy to know when you need to make conversions.
An all-pass filter shifts the phase of the signal, but more importantly it has group delay. All frequencies below the nominal 3dB frequency of the filter are delayed, and this remains satisfactorily consistent up to about one fifth of the 3dB frequency. If the 3dB point is (say) 13kHz, the group delay will be almost perfectly flat up to 2.6kHz. It's often considered that 3rd order all-pass networks are likely to provide the optimum response with most systems, requiring three opamps, however using a 4th order delay offers some advantages. The topology of the networks isn't important, but a cascade of 1st order networks is by far the easiest to configure. However, if you need flat group delay to at least 10kHz, the simple approach is not optimal.
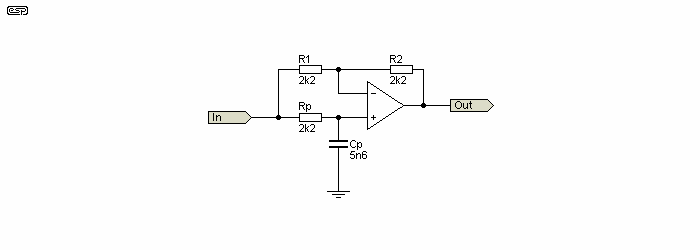
Figure 3.1 - 1st Order Phase Shift Network
Figure 3.1 shows the basic 1st order all-pass filter, which is the basis for most of those that follow. As noted above, in the majority of systems you'll need to use a 3rd order network, because it's usually impossible to get enough group delay with a high enough upper 3dB frequency with less. With the values shown, the 3dB frequency corresponds to 90° of phase shift, and this is at 12.9kHz. Note that adding sections does not affect the 90° phase shift frequency, but it does increase the overall group delay.
f90 = 1 / ( 2π × Rp × Cp )
f90 = 1 / ( 2π × 2.2k × 5.6nF ) = 12.9kHz
At this frequency, the group delay is half of that obtained at lower frequencies. It's important that the phase shift and group delay are not significantly affected at the crossover frequency, because that makes the end result far less predictable. Low frequency group delay is equal to twice the time constant of the resistor and capacitor, so ...
Group Delay = Rp × Cp × 2
Group Delay = 2.2k × 5.6nF × 2 = 24.64µs
Adding another section identical to the above creates a 2nd order network, and the only thing of importance (group delay) is doubled. If a third section is added, the group delay is 74µs - three times that of a single network. At 2.5kHz the group delay is a bit less - 71µs. This is less than desired, but may be ok, depending on the crossover frequency and slope.
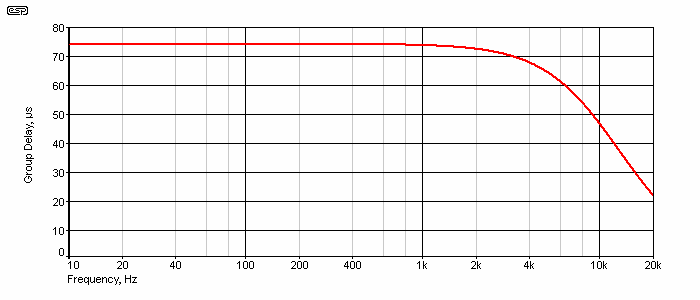
Figure 3.2 - Group Delay, 3rd Order Network
Figure 3.2 shows the group delay obtained with three identical networks, all using the Figure 3.1 circuit. The delay obtained is flat from zero to 1kHz, and is 10% down (66.5µs) at 4.32kHz. As shown above (notably Figure 1.3), this still provides a summed electrical response that's almost completely flat. This can sometimes be improved by adding a fourth network, but it's usually not necessary. Ideally, the delay would remain the same up to at least twice the crossover frequency, but this means a shorter time constant for each delay circuit, and the subsequent increase in the number needed.
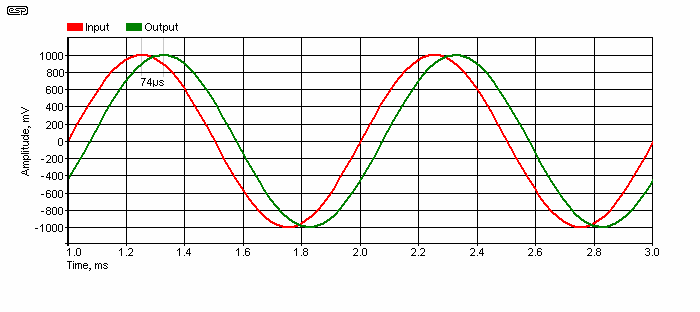
Figure 3.3 - Delay at 1kHz, 3rd Order Network
Talking about group delay may not mean a great deal as shown in Figure 3.2, so the signal waveform is shown above. The red trace shows the input to the network, and the green trace is the output. You can see that the output is delayed by 74µs. This is what you'll see on an oscilloscope, since they don't have the facility to show group delay. If you have a digital scope, you can set the cursors to the peak of the input and output waveforms, and measure the delay that way. You can measure the delay at any frequency, and below 1kHz it remains constant. Above 1kHz, the amount of delay reduces with increasing frequency. Without an oscilloscope (or a simulator), it's very difficult to detect the delay.
Simply using a series of identical networks may seem like a rather pedestrian way to achieve our goal. A second-order network would appear (at least on the surface) to be more 'elegant', but it uses nearly the same number of parts (more if the inverter is included), and has higher component sensitivity [ 3 ]. It's not as easy as simply working out the 90° frequency (to ensure it's well away from the crossover frequency) and determining the group delay with a simple formula. Once we have to use odd-value precision components, the task becomes tedious and error-prone. A second order network is also inverting, where a pair of cascaded first order networks is not (assuming that you use the version shown here, having a resistor feed and a capacitor to ground).
As most regular readers will know by now, if there's a simple and a complex way to achieve the same goal, I will always opt for the simpler approach - provided it doesn't compromise performance. This is a case in point. While you can certainly use a second order phase shift network followed by a first order network to obtain an overall 3rd order network, there is no point if it makes the design more sensitive to component values, and/ or requires the use of odd value resistors (the caps don't change). Both use the same number of opamps, resistors and capacitors, so there's no saving.
Both networks shown here have close to 73µs delay, and without any changes to Figure 4.2 they have identical performance. The difference is that the Figure 4.2 circuit can be improved slightly, to provide the same group delay (give or take a couple of microseconds), but with improved flatness with increasing frequency. Some may find this appealing.

Figure 4.1 - 2 x 1st Order Networks
While the above circuit works perfectly, it may be seen by some as 'old school'. There is an alternative shown below, but despite the requirement for an inverter to maintain the signal polarity, the performance of the two is identical. You'll also note that there's a requirement for odd value resistors in the feedback networks, which detract from its simplicity. The Figure 3A circuit uses identical sections, and all resistor values can be the same. The phase determining resistors are shown as 2.2k, but they may need to be changed to get the required phase shift and group delay. With the values given, the group delay is 49µs.
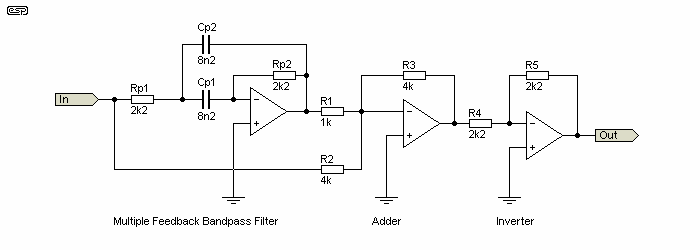
Figure 4.2 - 2nd Order Network
This is a second-order phase shift network, implemented with a multiple feedback (MFB) bandpass filter followed by an adder (subtractor if you prefer). The filter Q is 0.5, and the tuning frequency is 7.2kHz with the values given. It's performance is the same as the Figure 4.1 network, but to ensure there's no signal inversion, the final inverter stage is required. Without the inverter, the signal polarity is reversed (180°) which will usually be inconvenient. There is no immediately apparent advantage using the Figure 4.2 circuit for a second order delay, and the requirement for the inverter makes it even less attractive.
Alternative delays can be achieved by scaling Rp1 and Rp2 and Cp1 and Cp2. The group delay of the two versions is identical when the same values are used for Rp and Cp. The responses are shown below.
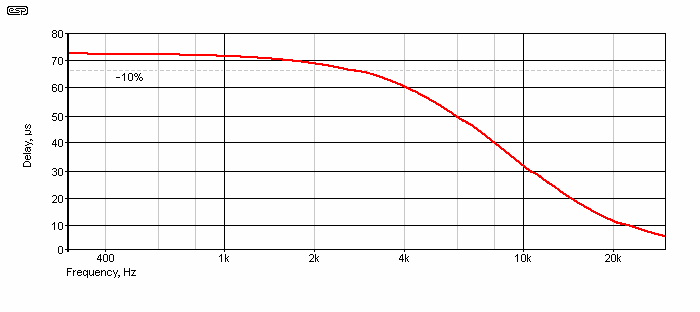
Figure 4.3 - Group Delay, Figure 4.1 - Red, Figure 4.2 - Green
The green trace is not visible, because it lies directly below the red trace - they are perfectly aligned. There's a lot to be said for circuitry that remains benign, and where it is easy to calculate the values. MFB filters are useful, but they can be difficult to work with, and doubly so when they are combined with other circuitry as shown here. There is no apparent advantage to the more complex network, and indeed, the opposite is true.
Note that I have elected not to provide the design formulae for the second order network. If it's something you'd like to play with yourself, see Reference 3 which has everything you need and more. The same applies to the Figure 5.2 third order version. While I could provide these data, for most hobbyists it's unlikely that you'll be willing to pursue these more complex designs, especially since only the third order version provides a noticeable benefit (but at the cost of high component sensitivity. I particularly dislike recommending any circuit that requires odd values for resistance and/ or capacitance, because these are not likely to be found in anyone's 'junk box' (including my own).
Of course, the simplest is to cascade three first order networks. We know how to determine the delay easily, and we also know how to select the components for the required delay. Each stage adds its group delay to the total. We determined at the outset that a delay of 73µs was needed, suitable to move the acoustic centre of the tweeter back by 25mm. Each stage needs a little over 24µs delay, and the calculations are straightforward.
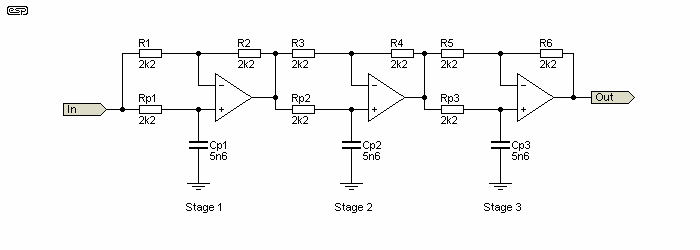
Figure 5.1 - 3 x 1st Order Networks
The next circuit is harder to recommend. It does have some good points, but they are overshadowed by its component sensitivity and the requirement for some inconvenient resistor values. It does let you get to a higher frequency for a given time delay, but the difficulty of calculating the values (which are critical) makes it less attractive than the simpler method shown above. There are no real component savings, as it has the same number of opamps and capacitors, and only one less resistor.
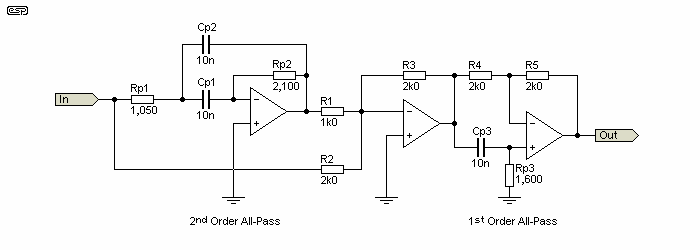
Figure 5.2 - 2nd Plus 1st Order Networks
This is where things get tricky. When the two circuits are added, component sensitivity becomes quite extreme, and working out the values needed is partway between a lottery and an exercise in advanced maths. Everything affects everything else, and changing the value of R1, R2 or R3 can affect the performance far more than you'd ever expect. While it certainly has an advantage that you can achieve very flat group delay up to much higher frequencies than the 'simple' version, if you don't use precision resistors and capacitors (nothing greater than 1%), the end result may be unsatisfactory.
Like most MFB circuits, the second version is very sensitive to component variations. A difference between the first two caps (Cp1, Cp2) of only 5% causes a peak or dip of over 1dB, and even Cp3 is critical. Basically, you need to use 1% tolerance parts for all resistors and capacitors. In comparison, no value is critical in the 'simple' version, and if 1% resistors are used throughout, no capacitance change will affect the frequency response. If the caps are not as calculated, group delay is affected, but that's to be expected. This makes the Figure 5.1 version far more attractive, as it uses just one more resistor, and component sensitivity is low. This makes it far better suited to experimentation, and you can easily add more 1st order sections if desired.
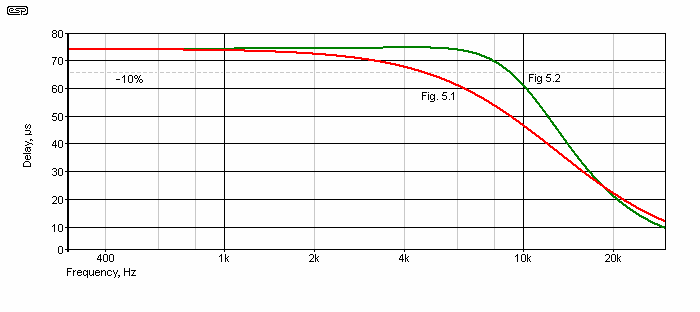
Figure 5.3 - Group Delay, Figure 5.1 - Red, Figure 5.2 - Green
As you can see, the two circuits are identical below 1kHz, and the 'simple' version is about 10% down (66µs) at 4kHz, somewhat shy of twice the crossover frequency. The Figure 5.2 circuit reaches almost 8.9kHz for the same reduction, so (at least in theory) it should give a better result. In reality (as shown in Figure 1.3) the end result is near perfect with either circuit. It's a slightly different matter with the lower order crossovers. If the Figure 5.2 network is used with a 6dB/ octave crossover, the ripple is reduced to just under ±1.5dB, with a 1.4dB dip occurring at 17kHz.
Applying the Figure 5.2 delay to a 12dB/ octave crossover gives a peak of 0.6dB at 2.84kHz. Perhaps surprisingly (perhaps?), this is worse than the response obtained with the 'simple' circuit, which has a maximum deviation of +0.29dB/ -0.23dB. It's not always obvious that a theoretically superior circuit can give results that are worse than a simpler version, but the comparison here shows that it can happen. Whether (or not) you will hear the difference is something that has to be tried - simulations work very well, but are 'perfect' - there's no 'real-world' variation in component values or parameters.
It may seem pedantic, but there is a very real difference between a phase shift induced group delay and an actual delay. Group delay is frequency dependent, and developing a circuit with constant group delay over the audio band is difficult using analogue electronics. One method is to use a length of coaxial cable, but when you need a delay of up to 100μs that becomes difficult. I doubt that anyone wants to accommodate 20kM (yes 20,000 metres) of RG58 coax just to obtain a delay of 100μs, but that's how much you'd need. A 'typical' coax cable has a propagation delay of about 5ns/ metre. This is significant for radio frequencies, but pretty much useless for audio. The method of choice now is a DSP, which can be programmed to apply any delay you like (within reason).
However, in an otherwise completely analogue circuit that means adding an ADC, the DSP and the a DAC to return to the analogue domain. While the difference (compared to a phase shift network) is certainly real, it's not generally a problem with loudspeaker systems. People have been using these simple circuits for many years to achieve time alignment, and the results are always 'good enough' for audio. The reasons for this are fairly simple - audio is slow. No instrument can produce an instantaneous pulse signal for example, with the possible exception of a synthesiser. However, these will always be set up to sound musical to a greater or lesser degree. The characteristics of instruments involve resonances, and the maximum rise-time is limited to how quickly a column of air or a piece of metal, wood or plastic can change direction.
These all provide real constraints on how quickly a sound can reach maximum amplitude, and how long it takes to decay. Another limitation is how quickly a loudspeaker diaphragm can move. Tweeters can obviously move much faster than woofers, and ultimately what we hear depends on our hearing. Up to perhaps 17-20 years old, we will be able to hear to 20kHz, but by age 40 that will be down to around 15kHz, and it decreases further with age. For a 60 year old listener, installing a super-tweeter to extend the range to 30kHz or more is obviously pointless. 
So, while a phase shift network is not a 'true' delay, it works well enough in practice to smooth out response anomalies in loudspeaker systems. A discrete impulse will not be delayed at all, and the phase shift network only mangles the waveshape. This may seem like a serious limitation, but it's immaterial in reality because discrete impulses are rarely a part of the music. They are certainly generated by clicks from vinyl playback, but I doubt that anyone really cares if they aren't reproduced perfectly - not being reproduced at all is generally preferred.
While the differences can certainly be demonstrated with simulations and graphs, I don't intend to go into further detail. This isn't because it's too hard, it's simply because it's irrelevant to the topic.
This article is intended as an overview, although the techniques (and simulated results) give results that will be very close to what you'll find via measurement. These are circuits where simulation and reality will be very close, provided the capacitors are the marked value (measurement is recommended to get them as close as possible). This is particularly important with the 2nd and 3rd order networks, and the capacitors should be selected to be within 1% for best results.
I've deliberately stayed clear of formulae for the more advanced techniques, because it's unlikely that they will hold much appeal. This is primarily due to the component sensitivity of anything other than the basic phase shift based delay circuits. The results are clear, and using a delay on the tweeter will almost always provide response that is flatter that you'll get without it, although with high-order crossover networks (e.g. 24dB/ octave) the extra fuss may not be warranted. Ultimately, it's only worthwhile if you spend a great deal on the drivers, and want the best possible outcome.
Normally, I suggest standard MKT (polyester) capacitors, but in this role I suggest that you opt for polypropylene for best results. They are larger and more expensive, but are warranted in a comparatively complex circuit intended to provide time delay and (hopefully) nothing else. Likewise, skimping on the opamps would be unwise, so for a stereo system it will not be a cheap undertaking. Whether it's worth the effort is something that only the constructor can answer. For experimentation, MKT polyester caps and TL072 opamps will be fine, and you might find that the end result is quite good enough to use in a system.
Determination of the exact delay needed can be difficult, and the networks themselves are superficially simple, but the high-order versions have hidden characteristics that aren't always clear from the descriptions. Ultimately (and despite the term 'phase shift network') we aren't interested in phase shift at all. The required parameter is group delay, and that has a limited frequency range before it starts to be reduced. While we would like it to extend for the full frequency range, it doesn't. Unfortunately, physics doesn't care what we'd like, it does what it is predestined to do, based on the component values we choose  .
.
It's well worthwhile to read Phase, Time and Distortion in Loudspeakers, which will help you to understand some of the 'finer' points. The article is fairly old now (18 years at the time of writing this), but nothing has changed. If I were to write the article now, it would undoubtedly have some of the information provided here (it only covers the basics), but it's not going to be re-written anytime soon.
An alternative that's sometimes used with passive crossovers is to apply a frequency offset (which also means a different phase response) in the hope of minimising response disturbances. While this can be made to work, it will almost always be an empirical approach, and will probably only work with the exact drivers specified. On occasion, you'll also see asymmetrical networks, having (for example) an 18dB/ octave filter for the tweeter and a 12dB/ octave filter for the midrange. This too can be made to work well, but almost always requires a time delay circuit or tweaks to the crossover component values to get a satisfactory result.
Overall, there remain far more reasons to use an active crossover and electronic networks to obtain the desired response. The best part with active networks is that there is no loudspeaker driver interaction, as each driver has its own amplifier. The opportunities to get everything exactly right are made a great deal easier, with only small, low cost parts needed to get results that will beat those from even the best of passive designs.
The use of a delay network is entirely dependent on your expectations and the relative driver offset. If the tweeter uses a waveguide, that will almost always move it back far enough that the acoustic centres of the tweeter and midrange are very close together, and no delay is necessary. Most people who have built the Project 09 24dB/ octave crossover have found that there's no need for a delay, because the dip created in most systems is less than the normal response variations from typical drivers.
 Main Index
Main Index Articles Index
Articles Index