

|
| Elliott Sound Products | Distortion & Feedback |
 Main Index
Main Index
 Articles Index
Articles Index
Let's make something completely clear before we continue. Yes, negative feedback can increase the level of higher order harmonics. Low order harmonic content is reduced, but harmonics that were previously below measurement thresholds may suddenly raise their ugly little heads to annoy and frustrate the designer. This generally only happens when small amounts of feedback are used around amplifiers that have limited gain and often rather poor performance to start with, but there might be exceptions (I've not found any so far). In many cases, while you may see distortion products that didn't exist before feedback was applied, you need to consider their level with respect to the primary signal. In many cases, it will (or should) become apparent that the level of any harmonics you see is below the noise floor, which makes them largely irrelevant.
The point of this article is to show that when properly implemented, negative feedback will invariably reduce distortion to levels that are well below audibility. Not just harmonic distortion, but the much more intrusive intermodulation distortion. If done incorrectly the results can be awful. There are many exciting possibilities that generally employ overly simplified circuitry, often in the mistaken belief that 'simple is better'. Albert Einstein is credited with saying that "Everything should be as simple as possible, but not simpler." Some attempts at amplifiers violate this rule, being either overly complex or too simple to be effective. Neither is useful.
However, it's important to understand that negative feedback does not necessarily reduce all harmonics by the same amount. There are myriad reasons for this, but one of the underlying issues is that amplifiers (or opamps) simply don't have the same gain at all frequencies, with the gain generally falling at high frequencies so the amount of feedback that's actually applied is not constant. In Class-AB amplifiers, the overall (open loop) gain may also fall at levels where the output transistors are carrying too little current to maintain a worthwhile overall open loop gain for the whole amplifier.
As with many things in electronics, we often make assumptions that don't necessarily hold true for a real-world circuit, and failure to understand this can lead to unexpected outcomes. In the material that follows, I've taken an admittedly 'simplistic' approach, not because I believe that feedback is a 'cure-all', but to make the information easy to understand at a fairly elementary level. Having said that, there is little doubt that the level of performance achieved from modern amplifiers (including opamps) cannot be achieved without the use of feedback. It doesn't matter much whether you like it or not, it's used in almost every circuit that demands linearity.
The last Reference shown is by Bruno Putzeys, and he explains that there is no such thing as "too much feedback". Many people may disagree, but that doesn't change the fact that he's right.
Needless to say, this article seems to have annoyed some people. One who posted anonymously on the ESP forum raised the issue (and even went to the trouble of 'proving' his point) and insists that established wisdom is correct, and therefore I am mistaken. Established wisdom is indeed correct if one approaches the problem the way it has been described (in great detail by Boyk and Sussman [ 5 ] for example). However, this is not the way amplifiers are designed, and is not the way they are normally used. While interesting, the findings are (IMO) rather pointless, because they do not describe a real-world use of the amplifying devices. Using 0.4mV input to a BJT amplifier with little or no feedback is not a normal application in a modern high fidelity system. One place this is sometimes used is with moving coil 'head' amplifiers, and with such low levels feedback can be omitted. However, the gain will change with supply voltage, temperature and (perhaps) whim. Feedback prevents gain variations and makes the circuit usable.
As for the criticisms raised, the first of these is terminology - degeneration vs. feedback. Although it is commonly accepted that emitter (source or cathode) degeneration is feedback, this is only partially true. It reduces gain and raises input impedance (as does negative feedback), but it has no effect on effective bandwidth or output impedance. Harold Black invented negative feedback, not degeneration (which pre-dated his invention). Degeneration is a form of feedback because it injects a portion of the output signal in series with the input (thus improving linearity), however, it provides no error correction facilities.
Harold Black's invention incorporated the error amplifier concept, although the term was not used at the time. It is worthwhile to examine the actual patent (U.S. Patent 2,102,671 filed in 1932, issued in 1937). Prior to Black's invention, a usually tiny amount of negative feedback was used to stabilise amplifiers against oscillation caused by positive feedback - this is more commonly known now as 'neutralisation'. It was (is) applied locally, not globally, and is mainly used with RF amplifiers.
The second criticism is based on the impossible - the perfect square-law device does not exist other than in mathematics. No real amplification device can produce a waveform with only second harmonic distortion. Using a simulation to prove a point and testing with something that does not exist in nature is at best pointless, and proves nothing. This point was covered (but ignored) in the initial version of this article, and obviously requires emphasis.
Of the possible options, using degeneration with a FET or BJT can introduce harmonics that did not appear before degeneration was applied. There have been some exhaustive examinations of this effect [ 5 ], but in general it only occurs at extremely low levels. Once the device is used in a real-world application, the effects generally become insignificant. This is something that has to be physically tested - throwing maths at it to get the result you first thought of is not helpful. The tests described apply to degeneration, not global negative feedback, and are not representative of most modern amplifiers.
Much of this work has been purely theoretical. In practice, any additional harmonics created by degeneration are likely to be below the noise floor, and are of limited significance.
The focus of the article is on 'true' negative feedback, not degeneration. The general principles described for negative feedback are not something I pulled out of my hat - I have seen countless claims that global feedback recirculates the signal (including Cheever [ 4 ], whose 'findings' are suspect at best). The feedback loop recirculates an instantaneous voltage - not the 'signal'. The (true analogue) signal consists of an infinite number of instantaneous voltages, and it is the designer's responsibility to ensure that the loop reacts quickly enough to be able to treat the input signal (at the highest frequency of interest) as an infinite number of instantaneous voltages.
In reality, this will never really be the case, but for the audio range one can come remarkably close. At no time does the 'signal' (assuming a discrete portion of a continuous waveform) pass through the feedback loop, as is often assumed. DIY audio critics have cited square waves, and these are dealt with in the article. Unless slow enough to remain within the amp's bandwidth, of course they will cause problems. Tests, claims or assertions based on irrelevant signals are equally irrelevant - not a difficult concept to grasp I would have thought.
In most cases where additional harmonics are realised by test or simulation, the feedback ratios are very low. That this is unrealistic and rather useless should be obvious, but that is exactly what the person who complained on the ESP forum did to 'prove' his point. The whole idea of negative feedback is that the circuit should have the highest practicable open loop gain. While performing tests where the open loop gain is only marginally higher than the closed loop gain will certainly prove the point (yes, additional harmonics can be produced under some conditions), the end result is not representative of the way that we use feedback. This is as meaningless as demanding that an amplifier should respond perfectly to signals that have components well outside the audio band (fast risetime squarewaves, for example).
The circuit shown in Figure 3 of this article is real. It works exactly as described, and this has been verified by simulation and experiment. This is probably one of the most compelling tests, yet has been ignored because 'conventional wisdom' has been challenged. If you doubt that it can be so, build it! I did, and it does just what I say it does. You don't need to worry about multiple synchronised oscillators, just inject any signal into the second opamp and watch it disappear as the feedback ratio is increased.
Just because something is taught at university or technical college, this does not make it so. I was taught that a common emitter/cathode amplifier had 'medium' output impedance, and common base/grid amps had 'high' output impedance. This was almost universally accepted (and probably still is in some cases), and is simply false. In both cases, the output impedance is the same as the collector/plate resistor - no more, no less. Only by testing, working with the devices and taking careful measurements will you find out what really happens. Relying on maths formulae (regurgitated ad nauseam) or 'common wisdom' is not always the best way to get to the truth.
The whole idea of the article was to debunk some of the more preposterous claims (Cheever, et al), and to stimulate further thought. Posts such as that by the anonymous poster show clearly that further thought has not been stimulated at all, but the same old claims are simply being repeated. Until such time as people look beyond the mantra and examine the situation in real-life, no progress is made. Negative feedback will never make a 'silk purse from a sow's ear' and it's not a panacea that can be used to cover up poor design. It's a tool that when used wisely, does what we expect and improves performance.
Now, you can either go back to what you were doing, or read the article (again), do some experiments (making sure that they represent real life), and then make comments. Nothing is set in stone, but I feel that the details given represent a shift from the way the issue is normally approached - hopefully for the better.
Claims abound regarding how 'bad' negative feedback is, how it ruins the sound, and how zero feedback amplifiers with comparatively vast amounts of distortion sound so much better with music. Entire papers have been written on the topic, new methods described to quantify the audibility of different harmonics, and new measurement techniques are suggested and described ad nauseam.
Of those papers, articles and semi-advertisements, many make completely incorrect assumptions as to how feedback actually functions in an amplifier, and some extrapolate these false assumptions to arrive at a completely nonsensical final outcome. Before continuing, we need to clear up one very important point ...
Feedback does not - repeat does not - cause the signal to travel from the output, back into the inverting input, and continue through the amplifier several (or multiple) times. At any instant in time, only a single voltage level is of interest.
Feel free to re-read that statement as many times as you need to. This is a claim that has been made on numerous occasions, and it is simply false. The whole idea of feedback is that it is as close as possible to instantaneous - feedback is applied to the input of an amplifier in direct proportion to the signal at the output, and for all intents and purposes at exactly the same time. (This means that the amplifier must be fast enough to keep up with the input signal at all times.) Only a voltage exists at any point in time, not a 'signal' and not 'audio', and the feedback works to make the instantaneous output voltage as close as possible to a replica of the instantaneous voltage at the input. With CD (for example) this happens 44,100 times per second, but with analogue it's a continuous process.
Once you have grasped the logic of how feedback actually works (as opposed to the way some people think it works), you are a long way towards understanding that many of the evils attributed to feedback are due to a lack of understanding, and have nothing to do with feedback itself. It has been claimed that applying feedback can actually increase the levels of higher order harmonics [ 1 ], however, this claim does not stand up to scrutiny (at least for any practical application). It is reasonable to expect that measurement errors or flawed assumptions are almost certainly the cause of this 'problem', but some parts of the industry will never let the truth get in the way of a good story. While it is true that in some (rather specific) cases application of feedback (or degeneration) can cause an increase of higher order harmonics [ 5 ], this is not (or should not be) the way the semiconductor (or valve) devices are generally used, so relevance is very limited.
Application of negative feedback (i.e. from output back to input, as opposed to degeneration) on single stage amplifiers with (often very) limited open loop gain and relatively high distortion will reduce the amplitude of low-order harmonics. With the small amount of feedback available and often with limited open-loop bandwidth, such circuits may indeed increase the levels of higher order harmonics. Sometimes they may not do anything of the sort.
However, it must be understood that such a circuit has very poor performance to start with. If a circuit has perhaps 3-5% THD without feedback, and has a gain of maybe 20 times, this cannot be considered a good start. Such a circuit will sound bad whether feedback is used or not - it's immaterial if some higher order harmonics are increased slightly. If you start with a bad circuit, you'll end up with a bad circuit. Feedback cannot (and does not) cure all ills, and expecting it to do so is unrealistic in the extreme. In such cases, it may be better not to use feedback - perhaps zero feedback makes such an amp sound 'less bad'. No amplifier with inherently poor linearity and low gain will ever sound good, even if measured distortion is reduced by adding small amounts of feedback.
For this article, it is expected (at least for the most part) that the circuit we start with has reasonably good linearity, and in particular has sufficient open loop gain at all frequencies of interest and at all signal levels for the feedback to be effective. Adding small amounts of feedback applied to already poor circuits is simply not sensible, and is not generally the way feedback is intended to be used. On occasion, feedback might be added just to reduce output impedance, and while this does work with low gain circuits, it's still comparatively ineffective. Just like distortion reduction, sufficient gain must be available to ensure that the circuit's parameters are determined by the feedback components rather than the amplifying devices.
When low gain circuits are used, applying feedback does not reduce the gain or output impedance by the expected amount. Gain is not a simple ratio defined by a pair of resistors, but becomes a complex interaction between the amplifying device and the feedback ratio.
For the majority of the tests described, the effects were simulated rather than measured. There are some very good reasons for this, with the primary reason being that the simulator has access to 'ideal' amplifiers. These have infinite bandwidth, infinite input impedance, zero distortion and zero output impedance. Being perfect, they also contribute zero noise. This enables one to perform experiments that simply cannot be done in the real world, and provide a level of accuracy that is also unattainable using real circuits. Likewise, the signal sources have zero distortion, so resolution exceeds anything attainable using actual circuitry. In addition, the simulator allows multiple different tests that are very time-consuming to perform on the test bench, and require all circuits to be built and analysed.
It is useful to understand what distortion is, and how it is produced. The generation of harmonics is not a weird function of a valve, transistor or MOSFET, but is a physics phenomenon that occurs whenever a waveform is not a pure sinewave. A pure tone contains only one frequency - the fundamental. By definition, this pure tone is a sinewave - no other waveform satisfies the criterion for purity. As soon as a sinewave is modified, the waveform that now exists is created by adding harmonics. Likewise, anything that adds harmonics changes the waveform - the two are inextricably intertwined. Amplifying devices do not add harmonics per se! Amplifying devices modify the waveshape, and this requires that harmonics are added to create the 'new' waveform. The creation of harmonics is a physics requirement, and has nothing (directly) to do with the type of device that caused the modification to the waveform. Devices with high linearity modify the sinewave less than devices with lower linearity, so fewer harmonics are created in the process.
Because the sinewave is a pure tone, it has long been used as a measure of the amount of non-linearity for amplifying devices. Even very small wave shape modifications can cause a large amount of distortion (and hence harmonic generation), and it is for this reason that sinewave THD (total harmonic distortion) tests are still used. Despite many claims to the contrary, a sinewave is not an 'easy' test - quite the reverse. Less than 1% distortion of a sinewave is easily heard (depending on the exact type of distortion), and it may be completely inaudible with some music or barely audible with others. Any device that amplifies will also distort, and the purity or otherwise of the output signal shows non-linearities very clearly. Interpretation of the test results does take some background knowledge though, and simply quoting a percentage with no qualifying parameters is completely useless.
Strictly speaking, simply turning a sinewave on or off causes distortion, because a truly pure tone is not only without harmonics, but has existed (and will continue to exist) for eternity. While this is real, no-one will ever take it to that extreme. If you doubt that this can be so, try measuring the distortion of a sinewave that's been fed through a tone burst generator (such as Project 143). Even with a perfect sinewave, the distortion will be over 5% THD (10 cycles on, 10 cycles off). The spectrum contains frequencies that are directly related to the switching frequency (on and off timing, in this case, 50Hz).
Because of the nature of a non-linear device which modifies the waveshape and thus causes the creation of harmonics, it should be obvious that it is not the amplifying device that generates the harmonics directly - it only modifies the waveshape. The harmonics are the result of the modified waveform - nothing more. To explain how a device modifies the waveform it is necessary only to look at the device's transfer function, and understand the process of amplification.
Amplification is an (almost) instantaneous process. An amplifier does not 'see' a complex waveform any more than we can experience all of last week simultaneously. As the Compact Disk medium has demonstrated, time can be separated into discrete fragments, and digital data can be derived that describes the instantaneous voltage at that point in time. This process is repeated 44,100 times each second. Compared to an analogue amplifier, this is very slow. The analogue domain does not use time fragments - all processing is done on a continuous basis - but, the amplifier is only capable of processing one instantaneous voltage level at any one time, and that's all it needs to do. The input voltage is a moving target, and the output signal follows it as closely as possible.
If an amplifying device has a gain of 10 when its (instantaneous) input voltage is 100mV, the output voltage will be 1V. If the device is non-linear, then the gain may fall to 9.5 when the input voltage is 1V, so the output will be 9.5V instead of 10V. This is distortion! That's it! The amplifying device does nothing more than change its gain slightly depending on the amplitude of voltage or current it has to deal with at any value of input voltage. It doesn't matter what device is used to create the non-linearity - bipolar transistors, junction FETs, MOSFETs and valves (vacuum tubes) are all non-linear, although in subtly different ways.
Intermodulation distortion (IMD) is another very interesting (and far more intrusive) effect of non-linear circuits. While this is covered in some detail below, it's still worth noting that this is another physical phenomenon. It doesn't matter if the non-linearity is caused by a transistor, valve, diode or corroded wires twisted together - the effect is the same for a given degree of non-linearity. Wherever there is harmonic distortion, there is also intermodulation distortion. The two cannot be separated, and if harmonic distortion is reduced, so too is intermodulation distortion (and of course, vice versa).
Of the forms of distortion that might be discussed, intermodulation is by far the worst. There simply is no 'nice' sounding intermodulation distortion, regardless of the topology of the amplifier. In very small amounts, and with some programme material, some listeners may like the sound of IMD, as it imparts a 'wall of sound' effect. High levels of IMD just sound dreadful with any recorded or reinforced music source.
Let's look at a common bipolar transistor as an example. The primary (but by no means only) form of distortion is caused by the internal emitter resistance of the transistor. Figure 1 shows a simple single transistor amplifier. A bias resistor is shown - it must be pointed out that this biasing method is never used in practice, because it is too dependent on device gain, temperature and supply voltage. Proper biasing that allows for thermal effects, device parameter spread, etc. is beyond the scope of this article.
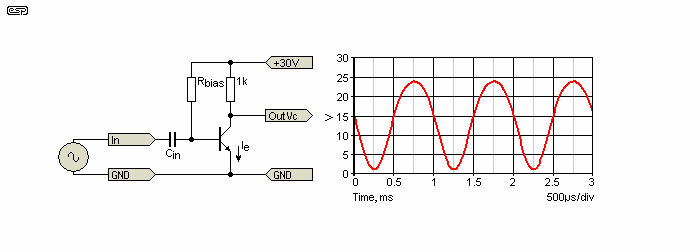
Figure 1 - Basic Single Transistor Amplifier
This is a very basic amplifier, but it embodies all the issues that face other amplifying devices as well - valves, JFETs and MOSFETs all have similar non-linearities, but for different reasons. It just happens that with a transistor it is easy to describe in simple terms. The output waveform is also shown, and distortion measures 12%, being second (-18.5dB), third (-52dB) and fourth (-56dB) harmonics. All others are over 90dB below the fundamental. It is generally taken that ...
re = 26 / Ie (mA) where re is the internal emitter resistance and Ie is the emitter current
The gain is determined by the ratio of the collector resistance to the emitter resistance, and is approximately ...
Av = Rc / ( Re + re ) where Av is voltage amplification, Rc is collector resistance, Re is external emitter resistance, and re as above
Re (the external emitter resistance) has not been included in the circuit of Figure 1, which has a gain of about 390. As we shall see, this varies over the output voltage range, so the measured value gives a false impression because of waveform modifications. Table 1 shows how much the circuit of Figure 1 will vary the emitter current and hence the (theoretical) gain, depending on signal level. The base current has been ignored, but this also has an influence - albeit rather small.
| Vc (Volts) | Ie (mA) | re (Ohms) | Voltage Gain |
| 29 | 1 | 26 | 38 |
| 25 | 5 | 5.20 | 192 |
| 21 | 9 | 2.89 | 346 |
| 17 | 3 | 2.00 | 500 |
| 13 | 17 | 1.53 | 654 |
| 9 | 21 | 1.24 | 807 |
| 5 | 25 | 1.04 | 962 |
| 1 | 29 | 0.89 | 1115 |
You can see from the table how the waveform of Figure 1 comes about. When the collector voltage is high, the current and gain are lower, and the waveform is flattened. When the collector voltage is low, the current and gain are much higher, so the waveform becomes elongated. As is obvious, the gain varies over a wide range, and any voltage waveform applied to the base must become distorted. Transistors show a logarithmic response when the base to emitter junction is driven from a voltage source, and table 1 shows this effect quite clearly.
Because the transfer function is non-linear, it must alter the wave shape. If the wave shape is altered, harmonics are produced. To reduce distortion (of all forms), the application of negative feedback will make the amplifier more linear, and this results in fewer harmonics. There is no mystery and no magic. It doesn't matter if the feedback is global (applied around a complete circuit) or local (applied to each device individually). In general, global feedback gives better results than local feedback, but only if the amplifier has high open loop gain (i.e. gain without feedback).
Prior to adding feedback, it is advantageous to improve the circuit's linearity by other means if possible. Since the gain of a transistor varies widely with emitter current, maintaining a constant current (via the collector) will help. Since transistors are current controlled, using a variable current for the input will also help - distortion can be halved by this alone, but voltage gain is reduced. In the case of the above circuit, using a 15mA constant current source instead of the 1k resistor increases the voltage gain to 3227, and reduces distortion to 4% - using current input (via a series resistor) reduces gain, but also reduces distortion even further.
The additional gain from the use of a current source load allows us to apply feedback - if the gain is set at 400 (close enough to the 390 measured before), distortion is reduced to 0.7%. The second harmonic is now -43dB, the third is -70dB and fourth is at -95dB (all with respect to the fundamental). Compare these figures with those obtained for the circuit as shown - no comparison! This is covered in more detail in Section 5.
Alternatively, Re (the external emitter resistance) can be added to create 'local feedback'. By adding an external resistor, we actually do nothing more than (partially) swamp the variation of re with emitter current. While this makes the circuit more linear, it is not really feedback at all - the correct term is degeneration. Gain variation (and hence distortion) is reduced because Re + re is much greater than just re alone and base current is also more linear, but one of the benefits that feedback (as opposed to emitter degeneration) gives is reduced output impedance. Emitter, cathode or source degeneration does not lower output impedance.
There is a great deal of information that was compiled a long time ago that seems to have been forgotten, dismissed, or simply neglected. Of particular interest is the section on distortion in the Radiotron Designer's Handbook [ 2 ]. Since some (many) of the detractors of negative feedback advocate single ended triode operation, one would expect that they would have examined what was considered 'high fidelity' back in 1957, rather than claim that amplifiers that were considered low fidelity back then represent high fidelity today. This is not a tenable position!
Of some interest is a table of harmonics based on a fundamental of C - taken for convenience as 250Hz. The table is reproduced below. It shows the musical relationship of each harmonic up to the 25th with respect to the fundamental, based on the natural or just musical scale (as opposed to the equally tempered scale that is used for most instrument tuning).
| Harmonic | Frequency | Note | Comment |
| 1st | 250 | C | Fundamental |
| 2nd | 500 | C1 | |
| 3rd | 750 | G | |
| 4th | 1000 | C2 | |
| 5th | 1250 | E | |
| 6th | 1500 | G | |
| 7th | 1750 | - | Dissonant |
| 8th | 2000 | C3 | |
| 9th | 2250 | D | |
| 10th | 2500 | E | |
| 11th | 2750 | - | Dissonant |
| 12th | 3000 | G | |
| 13th | 3250 | - | Dissonant |
| 14th | 3500 | - | Dissonant |
| 15th | 3750 | B | |
| 16th | 4000 | C4 | |
| 17th | 4250 | - | Dissonant |
| 18th | 4500 | D | |
| 19th | 4750 | - | Dissonant |
| 20th | 5000 | E | |
| 21st | 5250 | - | Dissonant |
| 22nd | 5500 | - | Dissonant |
| 23rd | 5750 | - | Dissonant |
| 24th | 6000 | G | |
| 25th | 6250 | G# | Dissonant |
Obviously, harmonic distortion that extends to the 7th or beyond is to be avoided. It is (or was) well known to guitar amp manufacturers that the seventh harmonic and above should not be reproduced if possible (even during overdrive conditions) because of just this issue - discordant (or dissonant) harmonics simply don't sound nice.
Another table shows the levels of distortion that were considered objectionable, tolerable and perceptible for various frequency limits and triode or pentode valves. This table is also reproduced, but I have only included the 15kHz bandwidth results - other bandwidths were listed, but no-one would consider a bandwidth of 3,750Hz acceptable these days.
| Source | Mode | Distortion | Comments |
| Music | Triode | 2.5% | Objectionable |
| Pentode | 2.0% | ||
| Speech | Triode | 4.4% | |
| Pentode | 3.0% | ||
| Music | Triode | 1.8% | Tolerable |
| Pentode | 1.35% | ||
| Speech | Triode | 2.8% | |
| Pentode | 1.9% | ||
| Music | Triode | 0.75% | Perceptible |
| Pentode | 0.7% | ||
| Speech | Triode | 0.9% | |
| Pentode | 0.9% | ||
These figures are interesting compared to amplifiers of today. Both triode and pentode amplifiers used in the test had an output of 3W, and were conducted in a 'typical' listening environment. While modern (competent) transistor amps will invariably beat the distortion criteria by a wide margin (at any level or frequency), some modern SET amps seem to be considerably worse than one would hope, many having distortion that rates as objectionable - and this table was compiled was a very long time ago indeed.
For those who have access to the complete text of the Designer's Handbook (or at least Chapter 14 which concentrates on fidelity and distortion) I strongly recommend that it be read in its entirety. There is a great deal more to it than I have the space to reproduce here, and the fundamental principles have not really changed, despite the passing of the decades since it was written.
There is an informative section covering intermodulation distortion, in which it is pointed out that there is no direct correlation between THD and IMD. It is also pointed out that no actual amplifier has only second or third harmonic distortion - every form of distortion is accompanied by multiple harmonics, although either even or odd harmonics can be the most dominant. Note that it is now possible to build a circuit where odd-order harmonics are several orders of magnitude greater than even-order harmonics, and for all intents and purposes there are no even-order harmonics present. This wasn't possible when the book was written.
Negative feedback (or just feedback) has been used for many years to linearise amplifiers. Between 1935 and 1937, Harold Black of AT&T received three U.S. patents relating to his work on the problem of reducing distortion in amplifiers by means of negative feedback. The invention caused little controversy for many years, but eventually this happy situation had to end - at least in the hi-fi industry. Feedback is used extensively in medical, military, aerospace and industrial applications and seems not to cause any problems there, despite its bad reputation amongst some audiophiles.
Although many of the early attempts were less than perfect, it must be understood that the results without the feedback would have been many times worse. Negative feedback cannot make a dreadful amplifier sound good, but may make it sound acceptable. There is no possibility that the use of feedback will make a good amplifier sound bad. Not only are distortion components reduced, but negative feedback also increases the input impedance, reduces output impedance, and linearises frequency response. It is not a panacea, but it does come very close.
So, let us examine what feedback really does. Figure 2 shows the basics of a gain block - in this case, an operational amplifier (opamp). It may be comprised of any number of devices, and the active components can be valves (tubes), transistors, FETs, MOSFETs or any combination thereof. The gain block will be assumed to have infinite gain and infinite bandwidth for the initial analysis - we all know this is not possible, but it makes understanding the principle easier.
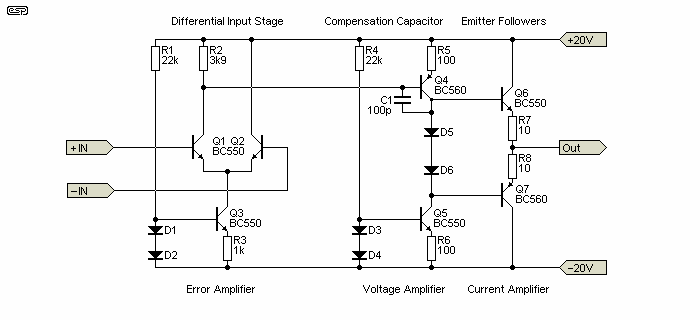
Figure 2 - Basic Feedback Analysis Circuit
An amplifier (power amplifier of conventional topology, opamp, etc), consists of three discrete stages. These are ...
Each of these may be as simple or complex as desired or needed, and each can use a different technology. The functions of each stage are (or will become) self explanatory, and a quick look at any of the project amplifiers (e.g. P101, P3A, etc.) will show that the same basic stages are used in most amplifiers.
If you have read the article Designing With Opamps, you will know the two rules of opamps (a typical semiconductor power amplifier may be thought of as an opamp for all intents and purposes). These rules are ...In any linear circuit, rule #2 is inapplicable unless there is a fault or overload condition, so only rule #1 needs be considered for this discussion. As shown below, a voltage of 1V is applied to the non-inverting input - the normal input for an audio amplifier. I will state at the outset that only one thing is important - the value of the voltage presented. We need not concern ourselves with frequency - indeed, time is utterly inconsequential (at least for a basic theoretical discussion).
Referring to the practical circuit shown in Figure 9, in order to fulfil rule #1, the amplifier's output voltage must be exactly 11V. This assumes that the open loop gain (without feedback) is at least 100 times greater (but preferably more) than the desired gain with feedback. The figure of 11 is simply derived from the voltage divider formula ...
Vout = Vin × ( R1 / R2 + 1 ) Where Vout is the voltage at the -ve input and Vin is the voltage at the amplifier outputTherefore, at the inverting input we should measure ...
V-in = 11 / ( 10k / 1k + 1 ) = 11 / 11 = 1V
The first rule is satisfied, and the system is stable. The error amplifier is the critical element here. If the input voltage changes, the error amplifier simply detects that its two inputs are no longer the same, so commands the VAS to correct the output until equilibrium is restored. This is not an iterative process, which is to say that the amplifier does not keep feeding the input signal (meaning a significant part of the input waveform) into the inverting input to be re-amplified, re-distorted and re-compared. This is where some of those who criticise negative feedback have made their first error.
The output of the amplifier simply keeps changing in the appropriate direction until the error amp detects that the voltages are again identical, at which point the output of the error amp ideally just stops where it is, and so does the rest of the chain. In reality, there will be a small amount of instantaneous correction as the two voltages approach equality, but this must happen much faster than the input signal can change with normal programme material.
The fact that the correction is usually done well before the input voltage has even changed significantly clearly means that no part of the feedback signal is fed through the amplifier over and over again - that just doesn't happen. In our ideal device, the change is instant, in a real device it is possible to measure the time it takes for the correction to be made. For an audio amplifier, the correction must be completed faster than the highest frequency of interest can change - how much faster is open to some conjecture, and that will be looked at later in this article.
All amplifying devices have some distortion. Desirable though it may be, a distortion free amplifier doesn't exist - other than in a simulator. Some opamps come very close (with feedback), but inherent non-linearities within the amplification chain are inevitable. Without feedback, the distortion components tend to be low order (i.e. second, third, fourth, etc., with diminishing amplitudes as the order increases. The application of negative feedback reduces the amplitude of these harmonics (hence the term harmonic distortion), in direct proportion to the amount of feedback applied.
A common claim is that, because the feedback signal is re-amplified, the distortion components are subjected to additional distortion. This supposedly creates high order harmonics that did not exist as a result of the original distortion mechanism in the amplifier. Since the feedback acts as an ultra-high-speed servo system, it is difficult to imagine why it is assumed that high-order harmonics are 'generated'. They are not generated at all, but simply become more easily measured because all the lower harmonic clutter is removed (in part at least).
However, if simple (single amplifying device) amplifiers are analysed carefully, it will be found that additional harmonics are generated when feedback is applied. The issue is generally that only a small amount of feedback can be used because the device gain is not high enough to allow more, and it's often 'degeneration' (using a resistor in the cathode/ source/ emitter circuit) rather than global feedback. This is a fairly complex area, and because such simple amplifying stages have largely fallen from favour, I don't propose to go into to any detail on this. It usually doesn't happen with high gain circuits such as opamps or power amplifiers unless the designer does something unwise.
Also notable is that any signal that is created within the feedback loop (most commonly noise) is also cancelled (within the open-loop gain constraints of the amplifier) by global feedback. Because noise (or distortion) generate signals that did not exist at the input, the error amplifier 'sees' any such extraneous signal as a deviation from the input signal, and cancels it to the best of its abilities. Note that input device noise is not cancelled, because the error amplifier cannot differentiate between noise it has created and the input signal.
That this works was amply demonstrated many years ago when the only cheap opamp was the venerable uA741 and a few others of similar noise performance. These are (still) notoriously noisy, so many designers added an external input stage using low noise transistors. This addition reduced the noise to acceptable levels, even for sensitive high-gain amplifiers as used for phono preamps and tape head amplifiers. The external transistors formed the error amplifier, and being low noise types were able to cancel out much of the opamp's internally generated noise - the additional gain also improved distortion performance.
This ability of the feedback loop to cancel internally generated signals (be it noise or distortion products) is so critical to your understanding of feedback that I have included a circuit and simulation results. These probably show more clearly than any other method how feedback works to remove anything that is not in the original input signal, by using the error amplifier to correct the output by applying an 'anti-distortion' component to the amplification stages within the feedback loop.
Figure 3 - Injection of Harmonics Into Feedback Loop
All signal sources have the frequency indicated, and all are set for an output of 1V peak (707mV RMS). Because of the simulator, there is no concern with frequency drift, so the distortion waveform will remain the same - this test can be run easily with real opamps, but attempting any harmonic relationship is pointless because the frequencies will drift. If you have access to synchronised oscillators it's not a problem, but I don't, and I doubt many others will either.
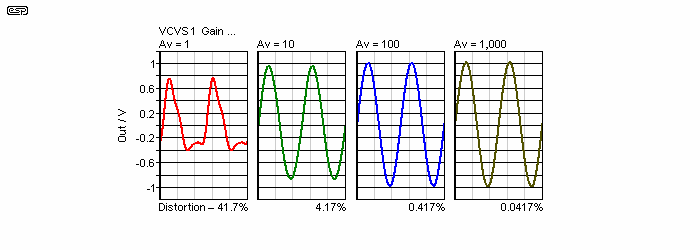
Figure 4 - Output Waveforms vs. Open Loop Gain
The first waveform is with VCVS1 set for unity gain. There is some degeneration, but no feedback as such. If the feedback loop is disconnected, the waveform remains the same, but at a slightly higher amplitude. As the gain of VCVS1 is increased (only the gain of the first stage (error amplifier) is changed), the distortion is reduced in direct proportion to the error amplifier's gain. There is no point reproducing a spectrum for this test, as the relationships are fixed by the 2, 3 and 4kHz signal sources. Only the total amplitude of the 'harmonics' is reduced with respect to the fundamental.
Although the circuit shown is configured as a unity gain buffer, adding feedback resistors to give the circuit gain makes no difference to its ability to remove the injected harmonics. To verify this, the error amp was set to a gain of 10, and the gain of the whole stage was increased to 10 by means of a 9k resistor from output to inverting input, and 1k from inverting input to ground. There was a significant gain error (Av = 5 rather than 10 as set by the resistors), but the rejection of the extraneous signals was just as effective.
Likewise when the error amp's gain was 100 (Av = 9.09) and 1000 (Av = 9.9). This is normal behaviour for an opamp - the open loop gain ideally needs to be 1,000 times greater than the required gain to achieve gain accuracy of 0.1%. While interesting and useful to know, that is not relevant to this article.
The above circuit will work with opamps too. Voltage controlled voltage sources are convenient in the simulator because their gain can be changed where one has no control over the open loop gain of an opamp, and some changes are needed to make a 'real' opamp work. However, the same distortion reduction is clearly evident - this has been tested and verified using real opamps.
Sorry, but yes  . A negative feedback system may be thought of as a servo, but that won't help anyone who is not familiar with servos. A toilet cistern is another matter - everyone has seen one, although not everyone has looked inside. I encourage you to do so
. A negative feedback system may be thought of as a servo, but that won't help anyone who is not familiar with servos. A toilet cistern is another matter - everyone has seen one, although not everyone has looked inside. I encourage you to do so  . The cistern is a good example of a simple negative feedback system. Unlike an amplifier (which is bipolar - it can generate positive and negative output voltages), a cistern is more like a regulated power supply - these also use negative feedback to maintain a stable voltage.
. The cistern is a good example of a simple negative feedback system. Unlike an amplifier (which is bipolar - it can generate positive and negative output voltages), a cistern is more like a regulated power supply - these also use negative feedback to maintain a stable voltage.
When water is let out of a cistern, the water level falls, and this in turn opens a valve. The water is replaced until such time as the level is restored to its original preset level. If water is allowed to escape at a low but variable rate, the float valve (ball cock) will regulate the water level (more or less) perfectly (Note 1), maintaining the same level even as you allow more or less water to escape. This is a simple example of negative feedback at work in your bathroom. For expedience, I have neglected the uncertainties of the mechanical linkages and valves (as well as the inertia of the water itself), but you knew that already.
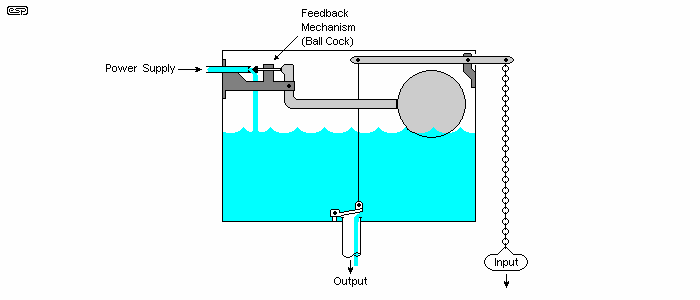
Figure 5 - Water Analogy of Feedback System
Should the water be allowed to escape faster than it can be replenished, the system is in an overload condition. This is no different from an amplifier where the input signal changes faster than the output can - the system cannot keep up, so the output is 'distorted'. I am unsure if this will help, but if it does improve your understanding of negative feedback, then it was worth it.
- In any such case (whether water or electrons), the accuracy/ regulation of the system depends on the loop gain of the feedback system used. There is always a requirement for stability, and that affects the high frequency performance because high gain at high frequencies may cause instability. So, it's not 'perfect', but can be made to be vanishingly close if the system has enough gain.
For those in Australia, be aware that the above analogy cannot be used because our water reserves are too small to allow the luxury of playing with water. We will just have to imagine that it works  .
.
So, having established that the output signal is not re-amplified over and over again instantly removes one of the criticisms of negative feedback - that it creates frequencies that didn't exist before feedback was added (at least for high gain circuits with global feedback). Since there is no re-amplification of the signal, there will normally be no new frequencies created, other than the distortion of the waveform caused by device non-linearity. Figure 6 shows a simulation circuit, using a diode to create distortion [ 3 ]. Note that the voltage across the diode is dramatically reduced - it's less than 5mV RMS because the diode is conducting, and the VCVS with a gain of 300 is used only to restore the level. The distorted signal is enclosed within the feedback loop (Feedback) of a pair of VCVS (voltage controlled voltage sources - 'perfect' amplifiers in the world of the simulator). A second circuit (Open Loop) applies the same distortion, but simply amplifies the distorted signal to obtain the same RMS voltage. C1 and C2 provide DC blocking to remove the diode's forward voltage.
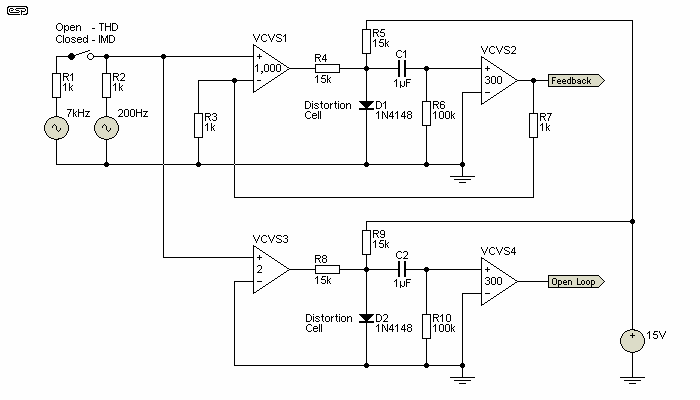
Figure 6 - Distortion Analysis Circuits
The applied input signal is 2V peak at 200Hz + 500mV peak at 7kHz, so we can see both harmonic and intermodulation products as generated by the non-linear element - a forward biased diode, passing ~15mA. This attenuates the signal greatly, and applies a controlled amount of distortion, measuring at 8.5% for a single frequency. In each case (feedback and open loop) the input voltage to the distortion cell was maintained at as close as practicable to the same level, although quite wide variations do not cause significant changes to the distortion level.
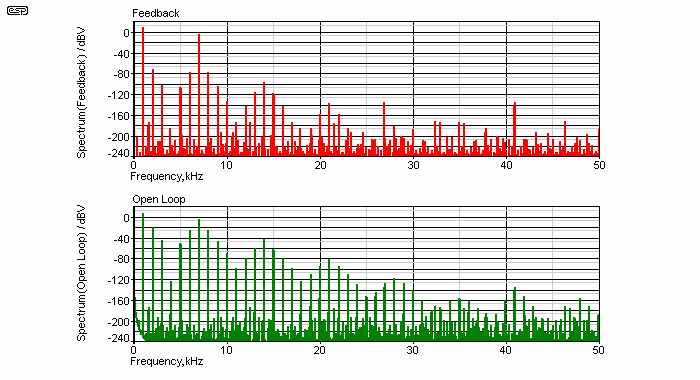
Figure 7 - Distortion Analysis Spectra (Red = Feedback, Green = Open Loop)
Looking closely at the FFT analysis of both the feedback and open loop circuits shows clearly that the distortion is reduced by the application of negative feedback. There is no evidence that any individual harmonic frequency is at a greater amplitude when feedback is applied, but you can see some signals that are not affected either way - these are simulation artifacts, and should be ignored. Note that the base level is -240dBV - this can never be achieved in reality, so you can ignore any value below -120dBV. Even this is rather adventurous, and -100dBV is more realistic.
Note the peaks at and around 14kHz, 21kHz, 28kHz and 35kHz. These are highly affected by feedback because they are harmonics and intermodulation products of the 200Hz and 7kHz input frequencies, and are virtually eliminated by applying feedback.
The spikes at 26.92kHz and 40.92kHz are not affected, because these are artifacts of the sampling rate (a simulator works in a manner similar to any digital system, and uses sampling to convert the 'analogue' signal into digital for processing).
For reference, I have also included a spectrum analysis for a single 1kHz sinewave. This makes the picture clearer, and is the way THD is measured using spectrum analysis. The harmonics are seen clearly, and it is notable that a circuit that one may assume would produce only even harmonics also produces odd harmonics. There is a school of 'thought' that is convinced that single-ended triode amplifiers (for example) produce only even ('nice') harmonics, while yucky push-pull amps produce only odd harmonics. This is not the case. While it is true that push-pull amps do indeed cancel the even harmonics, if the first claim were true, a push pull amp using triodes would cancel the even harmonics (which they do), leaving no distortion at all at the output (which they don't).
Even-order harmonic distortion in isolation does not happen - it is invariably accompanied by odd-order harmonics, as demonstrated by the open loop response shown below. Taking the 'even order distortion only' argument to extremes, in order to obtain only even order harmonic distortion, the first harmonic (the fundamental) cannot be present because it is an odd number! While a bridge rectifier can achieve this, the sound is unlikely to gain wide acceptance  .
.

Figure 8 - Harmonic Distortion - 1kHz (Red = Feedback, Green = Open Loop)
Note that the open loop distortion products show diminishing amounts of both odd and even harmonics. Only those up to the seventh harmonic (7kHz) are relevant - all others are more than 100dB below the fundamental. When feedback is applied, all of the distortion products are greater than 114dB below the fundamental. Also, note that not one distortion product is at a greater level than in the open loop circuit. The spectra shown only extend to 10kHz because there are no significant harmonics above that frequency. Reducing the gain of E1 reduces the feedback ratio and increases the level of the harmonics as one would expect. Changing from 100k to 10k (20dB) increases the amplitude of the harmonics by 20dB. If E1 is reduced to a gain of 1k, the second harmonic is increased to -74dB with respect to the fundamental. This effect is quite linear over a significant range.
As with the intermodulation test above, there are artifacts of the simulation and FFT process. The small peaks at 4.44kHz and 6.44kHz are not related to the 1kHz input signal, but are so far below the noise floor that it wouldn't matter if they were real. These signals exist in both cases (and at the same amplitude).
Having looked at some examples using ideal amplifying devices with no real-world limitations, it is now time to examine real circuits. Unlike their simulated counterparts, real amplifiers have finite bandwidth and slew rate (maximum rate of change), finite input and output impedances, and are not free of distortion. For the audio frequency range, this makes very little difference, despite claims that these limitations lead to Transient Intermodulation Distortion or 'TIM' - now pretty much universally discredited, but still quoted by some [ 4 ].
An amplifier simply needs to be somewhat faster than needed for the highest frequency of interest. Just as in the explanation given above, real amplifiers don't care if the input is AC, DC, or a mixture of multiple frequencies. The only things of interest are the instantaneous voltage level and the highest frequency of interest and its amplitude. These determines how quickly the output must change to prevent it from losing control.
One major limitation in any amplifier is propagation delay - how long it takes for a signal applied to the input to reach the output. Propagation delay depends on actual semiconductor delays, as well as phase shift introduced by the dominant pole capacitor. This component is almost invariably needed to maintain stability, because the amplifier must have less than unity gain when the total phase shift through the amp is 180°, otherwise it will oscillate.
Without the dominant pole compensation, propagation delays will be sufficient to cause a 180° phase shift while the amp still has significant gain. For example, if an amplifier has a propagation delay of 1µs, this causes the phase to be reversed at 500kHz, so the amp will oscillate strongly unless the gain is reduced to slightly less than unity for any frequency of 500kHz or above.
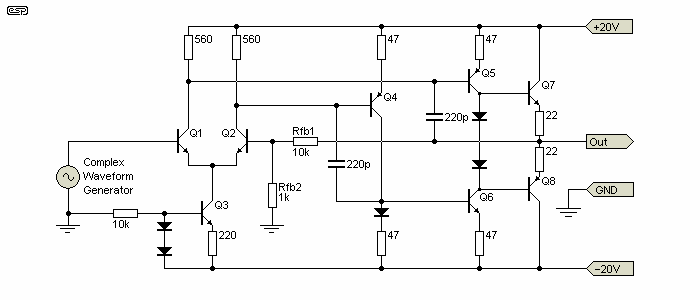
Figure 9 - Practical Feedback Amplifier
In order to obtain approximately equal slew rate for positive and negative going signals, the circuit of Figure 9 was used. Q1, Q2 and Q3 form the error amplifier, Q4, Q5 and Q6 make up the VAS, and Q7, Q8 form the current amplifier. Open loop gain is 20,000 (86dB), and the HF compensation caps (220pF) cause the open loop frequency response to be 3dB down at 2.4kHz. As is typical with such circuits, there is less feedback available at high frequencies because of the requirement for the dominant pole capacitor. This is not needed for open loop operation, but all linear (audio) applications will use the amplifier as a closed loop (feedback) circuit.
At an output voltage of 1kHz / 3.7V RMS, open loop distortion is 2.3%, showing that the circuit is fairly linear with no feedback. Input impedance is about 7k, with output impedance at about 200 ohms. The distortion components are low order as expected, with only second and third harmonics at significant levels. The fourth harmonic is at -85dB relative to the fundamental.
Adding feedback, but maintaining the output at the same voltage, things change much as we would expect. The gain is set to 11 (set by the feedback resistors Rfb1 and Rfb2). Distortion at 1kHz now measures 0.0014%, and only the fundamental is above -98dB (the level of the second harmonic with feedback). What happened to all the high order harmonics 'generated' by the addition of feedback? As fully expected from previous tests, they simply don't appear - all harmonics are suppressed to much the same degree, but with some dependence on the open loop gain (and hence feedback ratio).
With feedback, frequency response is -3dB at 4.3MHz (no, I don't really believe that either), input impedance a more respectable 5.8MΩ at low frequencies, falling to a bit under 1MΩ at 20kHz. Output impedance is well under 1 ohm. Apart from the rather optimistic frequency response reported by the simulator, the figures are pretty much what I would expect.
The slew rate is 11.5V/µs positive and 18V/µs negative - not exactly equal, but it will have to do. The maximum slew rate for a sinewave occurs at the zero-crossing point, and is determined by ...
Slew Rate ( Δv / Δt ) = ( 2π * Vpeak *× f ) / 106 V/µs
So, it we want to get 10V RMS output at 100kHz, the required slew rate is ...
Vpeak = V RMS × 1.414 = 10 × 1.414 = 14.14V
Slew Rate = ( 2π × 14.14 × 100k ) / 10^6 = 8.9 V/µs
Despite the gain rolloff after 2kHz and the relatively low slew rate for the desired frequency (it's not even double that needed for a positive going signal), the distortion measures 0.038%, and no harmonic exceeds a level of -70dB (with respect to the output of 10V RMS). The fifth harmonic is at -85dB. Remember that this is for a frequency of 100kHz.
The concept of TIM (Transient InterModulation distortion) aka TID (Transient Induced Distortion) was first proposed in the 1970s by Otala, and although it created a stir for a while, most designers realised fairly quickly that it does not happen in any sensibly designed amplifier. The 'dark side' of the industry seized upon TIM / TID as their 'proof' that feedback was bad, and the debate has raged ever since. Some supposedly objective works on the topic have glaring errors, or have completely ignored other factors [ 4 ], such as amplifier output impedance and its effect on the response of a loudspeaker. It is notable that almost without exception, driving a speaker with higher than normal impedance sounds 'better'. Frequency response is less linear, damping factor is (much) lower, but somehow it sounds really good - at least in the short term. However, it is a grave error not to eliminate this variable from a test, because the sound difference is usually unmistakable.
According to the theory, when an amplifier has feedback around it, the delays between the input and output changes will be such that huge amounts of TIM will be produced. Naturally, a sinewave will never show the effect (at any frequency), and traditional measurement techniques will be useless for identification of this mysterious distortion mechanism. A useful test is to apply a squarewave at (say) 1kHz, with a sinewave superimposed upon it. This test will certainly let you know if there is a problem, but although I have used the test many times on amplifiers that should have vast amounts of TIM, no problems have ever been seen.
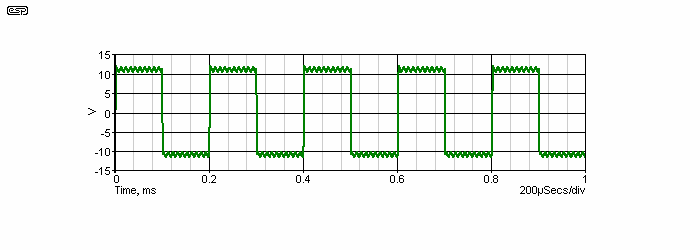
Figure 10 - TIM Test Waveform
Figure 10 shows the output waveform of the Figure 9 amplifier, which consists of a 10kHz squarewave whose slew rate is limited by the amplifier, with a 100kHz sinewave superimposed. This combined signal forces the amplifier into slew rate limiting, where the output cannot keep up with the input. The rise and fall times for the input squarewave are set at 1ns - many times faster than the amplifier can accommodate. Regardless of that, the sinewave shows very little modification - certainly there is a small section that is simply not reproduced at all, but this is with input frequencies and rise times that do not occur in any type of music!
Although a CD is capable of full output level at 20kHz (a slew rate of 5V/µs for a 100W / 8 ohm amplifier), such a signal will never occur in music. This is a good thing, because tweeters cannot take that much power anyway. An examination of the maximum level of any music signal vs. frequency will show that the level at 20kHz is at least 10dB below that in the mid band - 10W for the amplifier above, or a slew rate of 1.6V/us. No sensible designer will ever limit an amplifier to that extent, but allowing 5V/µs is easy, and will let the amplifier match the maximum rate of change of the CD source. In case you were wondering, vinyl can't hope to match a CD for output level at high frequencies, because at the first playing with the best cartridge and stylus available the high amplitude high frequency groves would be damaged forever. That vinyl can reach higher frequencies than CD is not disputed, but the level is very low. Fortunately, very high frequencies are never present in music at very high amplitudes.
As for claims that local feedback is 'good' and global feedback is 'bad' this is generally false. Global feedback around a competently designed amplifier will generally give much better results than multiple local feedback loops. Remember that waveform modification causes distortion, so a number of low gain stages with local feedback will generate additive distortion because each stage applies its own amount of modification to the signal! This is real, and the exact opposite of what may be claimed by local feedback proponents.
An amplifier with a single gain block and one global feedback loop will, provided it has reasonably good open loop linearity, simultaneously remove a significant amount of distortion from all stages at once, and there is no additive effect due to cascaded stages. This point is rarely (if ever) mentioned.
It is obvious that nothing in life is instantaneous. When a signal is applied to the input of an amplifier, there is a delay before the amplifier can react to the change, and this is determined by the speed of the devices used. Logic circuits typically have nanosecond delays from input to output, and this is also the order of delay one can expect before an amplifier as shown in Figure 9 will react to a change of input. According to the simulator, it takes about 5ns for the amp to respond to the fact that the input has changed - this is still using the very fast squarewave as an input. The output then swings in the appropriate direction at its maximum slew rate until the voltage at the inverting input again equals that at the non-inverting input. Once the voltages are equal, it takes about 220ns for the output to stabilise, settling so that the two input voltages are exactly the same. These times are very short - it takes the output 1.3µs to change from +11V to -11V, so the 'reaction' time is close to negligible. It would be pointless to try to reproduce all the waveforms, so I suggest that you download the simulations. The files are in SIMetrix format, and are ready to run.
Note that any delay has nothing to do with electrons 'slowing down' - there is typically nothing in an amplifier circuit that does any such thing. The delays are simply the result of the devices taking a finite time to turn on or switch off after a signal has been applied or removed, an issue that affects all amplifying devices. While painstaking engineering is needed to minimise these delays (especially for very high speed switching), it is generally not needed for audio - not because audio is slow (although it is very slow compared to the logic in a fast micro-processor), but because analogue amplifiers are not switching, so are normally inherently fast. We actually have to slow them down deliberately with a capacitor (the Miller or dominant pole cap) to prevent oscillation.
However, the above test was done with a signal that is much faster than the amplifier can handle (and much faster than any signal it is expected to handle for music reproduction), and it is more useful to examine what happens when the input slew rate is limited to something sensible. By adding a filter to the squarewave signal, the rise time can be limited to a somewhat more realistic value. A 32kHz, 24dB/octave filter was used, and this limits the output signal from the amplifier to 1.85V/µs - well within its range, but still a great deal faster than any real music signal will create. Everything is now within the linear capability of the amplifier. The output is delayed by 46ns compared to the input, but this is inconsequential. Of more importance is how the amplifier reacts to the combined sine and square wave signal. It is not immediately apparent from the output, but in fact the sinewave is almost completely unaffected - the portion that would otherwise be cut off due to slew rate limiting now simply 'rides' the slope of the squarewave - if compared (after correcting for the level difference), the input and output are virtually identical - there is no evidence whatsoever of anything that could be classified as transient distortion - even with a 100kHz signal.
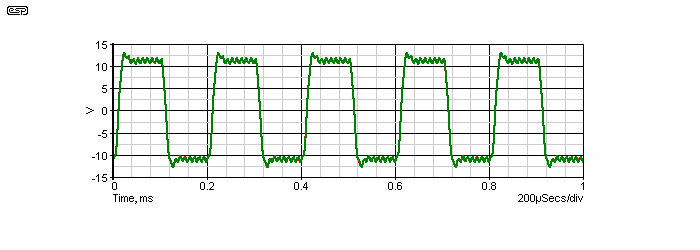
Figure 11 - Realistic TIM Test Waveform (Expanded)
There are two graphs in Figure 11 - green is the scaled input (increased in level to match the output) and red is the output signal. They are perfectly overlaid, indicating that the difference between them is very small indeed. Differences can be seen if the graph is expanded far enough, but the resolution of any oscilloscope will be such that the two waveforms will appear identical. The simulator can resolve details that are imperceptible with real test equipment. It is worth pointing out that the ESP sound impairment monitor (SIM) will detect the difference in real time using real world signals. Even the modified waveform of Figure 9 does not represent any signal that can be recorded or produced by any musical instrument (or combinations thereof).
Once the combined input signal is made sensible, the difference between the input and output signals can be seen, and it is primarily the result of the time delay (mainly phase shift) through the amplifier circuit. By using the SIM technique (measuring the voltage difference between the two inputs), all that remains is a residual signal that correlates with the gain of the amplifier at the frequencies used. The residual signal contains no non-linearities whatsoever, and is shown in Figure 12. The input stimulus this time is a 5kHz squarewave, filtered at 24dB/octave with a filter having a -3dB frequency of 32kHz. Superimposed on this is the same 100kHz signal used for the previous tests. The signal shown is the difference between the inverting and non-inverting inputs of the amplifier. Some of the signal shown is the result of the amplifier's error correction stage (the long-tailed pair) and VAS over-reacting slightly, and is also affected by the amplifier's total propagation delay and phase shift.

Figure 12 - Residual Signal Voltage From ESP SIM Circuit.
The important point here is that the amplifier must be maintained within its linear range. All amplifiers, including 'zero feedback' designs, can be forced outside their linear range. The whole idea of an amplifying circuit is that it should be linear, so no test signal should be used that dramatically exceeds the parameters of those of a normal source (such as music). To do so highlights 'problems' that do not exist in reality, so their inclusion is pointless at best, and grossly misleading at worst. The test signal used to obtain the above waveform is still a savage test - far more so than any music signal will produce, and deliberately much closer to the amplifier circuit's own limitations.
One can also measure the difference between an amplified version of the input signal, and that passing through the real circuit. In this case, the error signal is ~58dB down from the amplifier output, but is mainly the result of phase shift and very small gain errors - it is not a non-linear (distortion) component. At the upper test frequency of 100kHz, the amplifier has an open loop gain of only 470. With a design gain of 11 and an open loop gain of 470, the actual gain works out to be about 10.75 - this (as well as phase shift and DC offset) will always cause some error. It is important to understand that this is simply a small gain error, and does not contribute towards non-linear distortion.
These same tests have been performed (using test equipment, not the simulator) on various amplifiers shown in the project pages, with very similar results to those described above. There remains no evidence that any sensibly designed amplifier cannot keep up with recorded music, regardless of genre. The most common real amplifier fault one is likely to encounter in the listening room is clipping. Since clipping forces an amplifier out of its linear region, the main concern is how long the amp takes to recover from the overload.
This is a test I always perform, and a well behaved amp should recover almost instantly. The simulated circuit of Figure 9 recovers in less than 500ns for both positive and negative peaks, clipped with an input signal +4.5dB above the maximum level at 10kHz. Normal maximum level is 1.75V, and the input was driven with 3V (both are peak input levels). Recovery from clipping is not substantially affected by the input level. The recovery time is substantially less than the sampling rate of a CD (44.1kHz = 22.675us), so the loss of information is only a fraction of one sample. Most amplifiers should recover in a few microseconds. If they do not, then there is a problem with the design.
It's worth noting that even very slight and momentary clipping moves the amplifier out of its linear range, and the loss of some signal material is at least an order of magnitude worse than the effects of TID / TIM. Clipping is real, and can happen with any amplifier, whereas TID/ TIM usually only occur with unrealistically high slew rates on the input signal. Most TIM/ TID effects (assuming they actually exist with normal programme material) can be removed by the simple expedient of using a low pass filter before the amplifier, so fast risetime signals cannot affect the amp. Since musical instruments aren't terribly fast anyway, you needn't bother  .
.
I must point out here that I have used the term 'local feedback', even though it is more correctly called degeneration. The difference is subtle, and the distinction between the two is not usually explained. Degeneration only provides some of the benefits of true feedback - while input impedance is increased and gain and distortion are reduced, there is no effect on output impedance. 'Real' feedback will reduce output impedance as well. Degeneration may also have the opposite effect from feedback on noise performance with valves in particular. In such circuits, degeneration can increase the noise level - the cathode resistor must be bypassed for best noise performance.
There is a constant argument regarding the benefits of local rather than global feedback. The following two circuits show an essentially similar design, but one uses two stages with only local feedback, while the other has been optimised for global feedback. The value of the feedback resistor was adjusted to give identical overall gain, in this case 40 (32dB). Conventional transistor current sources were used in the second circuit, the only difference being the use of a voltage source instead of a pair of diodes. The difference is minimal.
The strange resistor values in the global feedback circuit were a matter of expedience, and were used to set the gain and collector currents so that both circuits were run with the same current and collector voltage. Normally, one would not go to so much trouble, but for this experiment it was important to eliminate as many variables as possible.
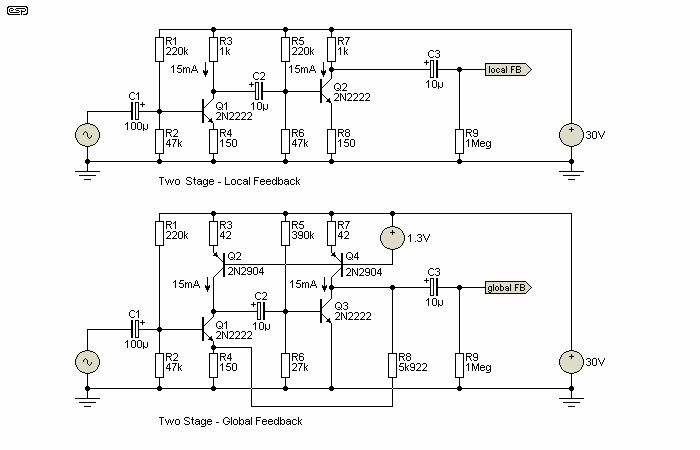
Figure 13 - Test Circuits for Local & Global Feedback
Even though the circuits shown are far too crude to be genuinely useful (although they will function perfectly as shown), there are some quite surprising results. The global feedback circuit has less than half the distortion of the local feedback version (0.035% vs. 0.082%), but there are many other advantages as well. Input impedance is higher (now limited by the bias resistors R1 & R2), output impedance lower, and global feedback makes the circuit faster and with better frequency response. The full listing is shown in Table 4, and it is obvious that global feedback is superior to local feedback in every respect.
| Parameter | Local FB | Global FB |
| Distortion | 0.082% | 0.035% |
| Input Impedance | 17kΩ | 37kΩ |
| Output Impedance | 1kΩ | <26Ω |
| -3dB Bandwidth | 10.4MHz | 24.7MHz |
| Open Loop Gain | 40 | 286,000 |
| Rise Time | 28.8ns | 11.9ns |
| Fall Time | 32.3ns | 10.6ns |
One would think that there must be a down side. Something so simple can't possibly be that much better without a sacrifice. Can it? Yes, it can. Figure 14 shows the spectrum of the two circuits. As you can see, global feedback reduces all the harmonics, and the 'nasty' third harmonic is reduced far more effectively by global feedback than local. Not what you might expect, but there it is.
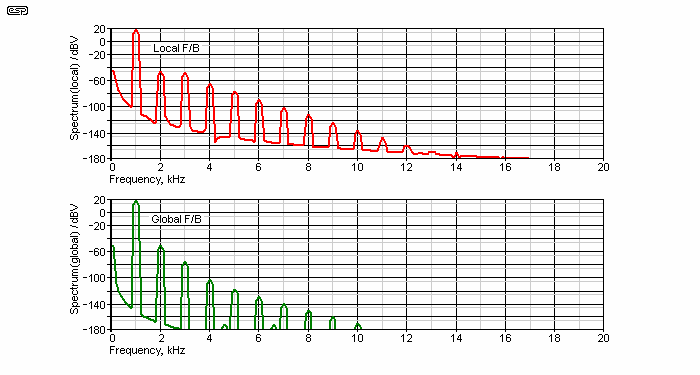
Figure 14 - Distortion Spectra for Local (Red) & Global (Green) Feedback
On the basis of this, global feedback wins on all counts. If you were to build the two circuits, you would find that the overall situation will not change, although some of the parameters will. This is due to component tolerance, variations in actual (as opposed to simulated) transistors and temperature, but will not materially affect the final outcome.
It is notable that global feedback works best when there is lots of it. The claims that global feedback should be used in moderation are just silly, and have never considered the reality of good circuit design. The higher the open loop gain the better, but eventually you will run into stability issues so some form of frequency compensation becomes essential.
Designing for stability and high open loop gain can be a challenge at times - especially for power amplifier circuits. However, when it is done (and done properly), there is no doubt that global feedback lives up to all the claims for it, with virtually no down side at all.
Well, there is a down side, but we have to look for it and know what we are looking for. Because nearly all opamp style amplifiers require a dominant pole capacitor to prevent oscillation, this causes a loss of open loop gain as frequency increases. Less open loop gain means less feedback, so upper harmonics are not attenuated as well as low order harmonics.
This could lead one to imagine that the application of feedback has indeed increased the level of the high order distortion components, but in fact it has done no such thing. What has happened is that the feedback at higher frequencies is insufficient to reduce the upper harmonics as effectively as those at lower frequencies. Their amplitudes have been reduced, but not by as much as the low order harmonics. High order distortion products can therefore be seen extending out well past the audio band, at a similar level to the lower order components. For example, we may find that the tenth harmonic is reduced to perhaps -80dB, but the eleventh is only at -81dB, the twelfth at perhaps -81.5dB and so on.
Examining the spectrum may show that the relative levels of all subsequent harmonics remain at much the same level, well beyond the audio band. In this respect, the addition of feedback can easily be blamed for all the upper harmonics. The problem really lies with the gain of the amplifier, which rolls off the frequency response at a lower frequency than we may desire. Regardless of claims you may see, there is no evidence to support the notion that harmonics outside the audio band are audible, or somehow create audible artifacts. Consider that very few tweeters extend much beyond 20kHz - some do go higher, but there's again no evidence that this improves anything (or is even audible to the majority of listeners).
The limited effect of feedback to remove crossover distortion can be seen plainly with an unbiased P101 MOSFET power amp. At 1kHz, there is virtually no visible crossover distortion, even when the output stage has zero quiescent current. At 10kHz, the distortion is clearly visible on the oscilloscope, even though it is not audible with a single tone (the 3rd harmonic being at 30kHz). Needless to say there is zero visible (and almost zero measurable) crossover distortion at 10kHz once the amp is biased correctly, but this highlights the open loop gain issue. At 10kHz there isn't enough feedback to be able to correct the crossover distortion, but there is enough gain at 1kHz to reduce it. There is more about crossover distortion in the next section.
The solution is simple enough - make sure the amp is as linear as possible before feedback is added (which in the above case means setting the bias current correctly). While there is no doubt that a wider open loop bandwidth is beneficial, this must never be at the expense of amplifier stability. A small amount of distortion at the uppermost frequency range is far better than an amp with marginal stability - oscillating amplifiers definitely don't sound very nice at all.
One area where there seems to be some misunderstanding is with crossover distortion. It always seems that no matter how much feedback you apply, crossover distortion will still be evident. The problem is that this is 100% true. The output stage of any amplifier must be linear before you apply feedback, or there will always be vestiges of distortion remaining.
Consider the case where the output transistors have no bias at all, so they cannot conduct until the base-emitter voltage reaches ~0.65V. When the output from the drive circuits (input stage and voltage amplifier stage - VAS) are less than 0.65V, the amplifier has no overall gain. None at all! If an amplifier has a gain of zero, feedback can't do anything to correct the output, so there is no feedback until the output of the VAS is greater than the forward voltage of the output devices.
This is one reason that the VAS is almost always designed to have a very high output impedance. This makes it a VCCS - voltage controlled current source. Having a high output impedance means that the voltage from the VAS will make an almost instantaneous transition at the bases of the upper (NPN) transistor to the lower (PNP) device, dramatically reducing the amount of measured (and heard) crossover distortion. However, there will still be measurable distortion because nothing in life is really instantaneous, and the overall gain at zero volts output is still zero.
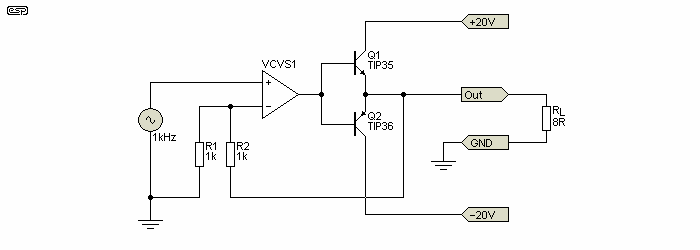
Figure 15 - Crossover Distortion Test Circuit
The above shows the general idea, and is a good test circuit to demonstrate crossover distortion. The circuit gain is set by the feedback resistors, and is set for a gain of two. The VCVS (voltage controlled voltage source) is set initially for a gain of 10, which is unrealistically low but used to demonstrate the idea. With such a low open-loop gain, the circuit cannot achieve a gain of two, and only manages an overall gain of 1.6 - the crossover distortion measures just over 2% with a 2V peak (1.414V RMS) input. This increases as the input level is reduced.
When the VCVS gain is increased to 100, distortion falls to 0.2% - exactly as expected. But it's still there, and will remain no matter how far the gain of the VCVS is increased. With a VCVS gain of 10,000 the open loop gain still falls to zero with very low input, and while distortion is reduced to 0.002% with a 1.4V RMS input, it's still 'pure' crossover distortion. With this combination, if the input voltage is reduced to 20µV the output will be around 6µV - exactly as anticipated, the voltage gain is less than unity because the output transistors are not conducting. Yes, this is an extreme demonstration (20µV is -94dBV), but it shows that crossover distortion can never be eliminated by feedback alone.
What we need to do is to add a bias circuit to ensure that the transistors conduct in the absence of signal (this is called quiescent current). While this ensures that the open loop gain never falls too far, it's still very important to use output devices whose gain doesn't fall to nothing at very low current. This was a problem with many of the early transistor amps - the output transistors had significant gain 'droop' at low current, so it was often still difficult to minimise crossover distortion.
Modern devices are very much better, and few modern amplifiers will have crossover distortion that is even close to the limits of audibility at any level. Most commonly, it should be almost impossible to measure it if the output stage is sufficiently linear without feedback. You can easily verify that even the most linear output transistors have very low gain at low current. Try measuring a power transistor with the transistor 'tester' that's built into many multimeters - they all operate at very low current, and a perfectly good output device might show a gain of less than 5 (some might even show zero gain).
The problem isn't the transistor, it's the tester. Transistor gain must always be measured at a realistic collector current. For output transistors, the minimum collector test current will be around the same value as the amplifier's designed quiescent current, typically between 10 and 50mA. Now you know why amplifiers aren't set up for a quiescent current of 2mA (for example) - that current is too low to ensure reasonable current gain with no (or very low) signal.
In most designs, the output stage is configured so that the driver transistors also provide some of the output current. This helps to ensure that the output stage always has at least some conduction to prevent the overall gain from falling too far.
In many of the examples shown above, I used a VCVS (voltage controlled voltage source) as the amplification device. This was done to ensure consistency of results under different conditions, but it's not particularly realistic when compared to an opamp or a power amplifier. These (almost) always include a Miller (aka 'dominant pole') capacitor to ensure closed loop stability. This plays an important role with distortion, because as the frequency increases, the amount of feedback decreases, at 6dB/ octave (20dB/ decade). The dominant pole must ensure that the amp/ opamp remains stable at the design gain. Most opamps are compensated for unity gain operation, and the -3dB frequency of the open-loop (zero AC feedback) is often only 100Hz, sometimes less.
That means that at 1kHz (one decade) the circuit's open loop gain has fallen by 20dB, 40dB at 10kHz and 60dB at 100kHz. If the circuit has an open-loop gain of 80dB (a gain of 10,000) at up to 10Hz or so and rolls off as described above, there's only 20dB of 'reserve' gain at 100kHz. If the stage gain is 20dB (×10), then there is no feedback at all at 100kHz. With no feedback, harmonics cannot be affected, and they will be visible using FFT or discrete frequency analysis.
When the bandwidth is severely limited, the circuit will almost certainly be affected by slew-rate distortion, caused by the dominant pole capacitor. Incoming (high frequency) sinewaves are converted to triangle waves simply because the circuit isn't fast enough to handle high levels at high frequencies. As already discussed, this is not usually a problem with audio, because high-level, high-frequency signals don't exist in music. The idea that 'fast' transients must create high levels at high frequencies is flawed, with one exception. With vinyl, you can get a fast, high-level transient if there's a scratch on the disc surface, but A) it's attenuated by the RIAA equalisation network, and B) who wants major flaws to be reproduced accurately anyway?
The use of a dominant pole within an amplifier (or opamp) circuit is claimed to guarantee that TID/ TIM (transient intermodulation distortion) will result, but that's a fallacy with programme material. Any power or op amp can be driven with a fast rise/ fall time impulse and will be limited by the slew rate, and this includes zero-feedback circuits! Realistically, these waveforms simply don't occur in music, so it's a moot point. Even a single transistor (BJT, JFET or MOSFET) has a finite maximum switching speed (effectively slew-rate), and a very fast transient can cause problems whether feedback is applied or not. It's obvious that the circuit must be able to handle the amplitude of the audio waveform (at all frequencies and levels of interest), but it's not at all obvious (or necessary) to ensure that frequencies that are ten times or more than the accepted maximum of 20kHz can be dealt with transparently.
Apart from anything else, providing much wider bandwidth than necessary makes the circuitry more responsive to RF interference. In extreme cases, it can even make a circuit prone to RF oscillation if there's even the slightest capacitive coupling between the input and output. Using feedback doesn't change this for better or worse, as it's simply a matter of gain and frequency response. I recently tested a simple design of a rather fast small power amp, and without a dominant pole capacitor it would oscillate cheerfully with as little as 2pF between input and output! The cap was essential just to ensure that the amp could not respond to stupidly high frequencies.
There are many opamps today that have such low distortion that 'trick' circuitry has to be used so it can be measured, even with the best equipment available. No-one can convince me that they can hear the distortion of any competent opamp, or that there are 'blindingly obvious' differences between them. The tests that allegedly 'prove' the hypothesis are subjective, never double-blind, and the experimenter expectancy effect (aka confirmation bias) simply makes the listener think there's an audible difference, when in fact probably none exists. The only subjective test methodology that can be trusted is double-blind!
As a side-issue (but just as relevant), if anyone claims that one opamp has 'better bass' than another, then you can pretty safely ignore everything else they claim. All opamps have response to DC, and no bass signal will cause any opamp to sound even slightly different from any other. This is one of the most puzzling claims I've ever heard, and it doesn't stand up to even the most rudimentary scrutiny! The same applies to many other claims. Don't believe me ... do your own research, take your own measurements and conduct properly designed double-blind tests.
Always consider a simple fact that applies to almost all recorded music. It's already passed through a great many stages of amplification, attenuation, equalisation, 'effects' (which may add distortion) and compression, any or all of which may be analogue or digital. Regardless, it's been processed by countless opamps (using lots of feedback of course), DACs, ADCs and the like, and may include valves (often also with feedback) in some cases. To imagine for an instant that the producers used 'zero feedback' designs throughout because they somehow knew that you don't like feedback is pure folly (and perhaps a wee bit naive).  Likewise, to believe that by some magical process, your 'zero feedback' design undoes all the alleged 'damage' caused during the production of your favourite music is high-order self-delusion.
Likewise, to believe that by some magical process, your 'zero feedback' design undoes all the alleged 'damage' caused during the production of your favourite music is high-order self-delusion.
Read any articles about distortion and feedback you may come across (including this!) with care. Like death and taxes, distortion is inevitable, however it can be minimised with careful design and a proper understanding of how feedback can be used most effectively to ensure that distortion doesn't spoil your listening experience.
Loudspeakers contribute far more distortion than the vast majority of amplifiers, but it's low order and surprisingly subtle. Some forms of (electronic) distortion can be very intrusive - especially crossover distortion in transistorised amps. Fortunately, it is a simple matter to design an amp using sensible circuitry and modern transistors where crossover distortion is (for all intents and purposes) non-existent. Total harmonic distortion figures of well below 0.1% at any normal power level from a few milliwatts to several hundred Watts are easy to obtain. The distortion of most modern amps will contain only a few low order harmonics at all power levels up to the onset of clipping.
Of far more concern is the addition of distortion to the recording, either deliberately or by accident. Nothing that you do in your home system can eliminate that - once a signal is distorted, you are stuck with it. It is possible to use an 'anti-distortion' circuit that reverses the distortion process, but that can only work if you know the exact nature of the distorted signal, and can produce its inverse and operate it with the exact same input level. Needless to say, this is not possible in any stand-alone system.
A big trap is to measure THD using a conventional distortion measuring set, but without monitoring the distortion residual either through a speaker or with an oscilloscope (preferably both). Early transistor amps gained a very bad reputation, because although the distortion measured much better than the valve amps they tried to replace, many had audible crossover distortion. Had the residual signal been examined with an oscilloscope, the designers of the day would have seen the problem immediately. Regrettably, this didn't happen (either by accident or intent is unknown), and this has provided endless ammunition for anti-solid state and anti-feedback proponents for well over three decades.
To avoid the use of global feedback based on some of the so-called 'research' is most unwise. As demonstrated above (and by many others), correctly used, global feedback is as close to a panacea as we are ever likely to find. The idea of any hi-fi system is to reproduce the source material as faithfully as possible, and to deliberately add distortion to everything you hear (due to amplifier deficiencies) because it sounds 'nice' is simply not high fidelity. If that is what you want to hear then there's no problem, but by adding so much additional material (by way of harmonics and intermodulation) you have a tailored sound system, not a hi-fi.
Harmonic distortion and intermodulation are linked together (although not in any mathematically predictable manner), so much so that it is virtually impossible to have one without the other. By ensuring that each element in the amplification chain is as linear as possible, you minimise both THD and IMD, both of which are easily demonstrable. This is a far better option than trying to minimise TIM, the very existence of which has been called into question countless times since it was 'discovered'.
Finally, I have included a pair of simple circuits that can be used to create distortion. Testing these using my workshop speaker system, the distortion of a 400Hz sinewave was (just) audible at < 0.5%. This same level would be inaudible on most music, being primarily low order as seen on the residual of my distortion meter. It is probable that had I used headphones or a better speaker system, low order distortion would be found to be audible at lower levels, but this simple test shows just how revealing a sinewave really is. While those trying to 'prove a point' will claim that a sinewave test is too simple and reveals little, this is obviously not the case.
As noted earlier, a sinewave is not an easy test at all, and anyone who claims otherwise is seriously mistaken. One only needs to see just how difficult it is to build a sinewave generator with very low distortion [ 6 ] to realise that any claim that a sinewave is 'simple' is unaware (blissfully or otherwise) of the reality. Good, very low distortion sinewave oscillators have been almost a 'holy grail', with many complex designs developed over the years in an attempt to get distortion well below the levels expected from modern opamps and power amps. Several sinewave generators are featured in the ESP projects section, and these show clearly how hard it is to create a low distortion sinewave.
Figure 16 - Distortion Test Circuits
The circuits shown will need to be carefully tweaked to suit your test equipment and amplifier, so consider them to be more of a general idea than definitive test circuits. The amount of distortion for both symmetrical and asymmetrical is adjusted by varying the input level, and no attempt has been made to level match the distorted and undistorted signals. The distortion itself is sufficiently prominent that full blind AB testing is not needed to get a general idea, but would be essential for a scientific study. The day after I did these tests, a friend came to my place, and I repeated the test with him. The distortion meter was disabled so we had no visual cue, and we arrived at almost exactly the same result with both test circuits.
Be aware that you may find that you can't hear any distortion until it is greater than the 0.5% I measured. Try moving around (even a few centimetres or so will be enough). Why? When listening to a steady tone, standing waves and reflections can combine to make a single frequency much louder than it should be, or almost inaudible. This effectively changes the distortion spectrum, making it sound much greater or less than the actual value. While this effect may have contributed to my hearing only 0.5% distortion on a sinewave, I did move around to make sure that the distortion was audible in more than one position. I neglected to measure the sound level when the test was done, but it would have been around 75dB SPL - any louder becomes very irritating.
For around 0.5% distortion measured and using an asymmetrical diode clipping circuit, the harmonic levels will be pretty close to the following (note that all harmonics are referenced to the level of the fundamental, all voltages are peak) ...
| Fundamental | 400Hz | 448mV | 0dB (reference) |
| 2nd harmonic | 800Hz | 1.35mV | -50dB |
| 3rd | 1.2kHz | 942µV | -53dB |
| 4th | 1.6kHz | 599µV | -57dB |
| 5th | 2.0kHz | 348µV | -62dB |
| 6th | 2.4kHz | 167µV | -68dB |
| 7th | 2.8kHz | 68µV | -76dB |
It is probable that only the first couple of harmonics would have been audible. Those above the fifth are approaching my hearing level threshold, and anything above the third is below the ambient noise floor in my workshop.
Sine waves are 'too simple' to use as a test? We think not!
¹ Much of the material is best considered bollocks, with some of it taking a giant leap into the overall category of bullshit. Read it by all means, but I recommend that you ignore 99% of what you come across.
SIMetrix Simulation Files Right click, and select 'save link as' from the menu.
To view or run these simulations, you need the SIMetrix simulator on your PC. The freeware version of the simulator can be downloaded from SIMetrix. Other simulators can also be used, but you will have to reconstruct the schematics.
 Main Index
Main Index
 Articles Index
Articles Index