

|
| Elliott Sound Products | Coax Cable Introduction |
 Main Index Main Index
 Articles Index Articles Index
|
Introduction
1 - Impedance
2 - Velocity Factor
3 - Coaxial Connectors
4 - Impedance Matching & Wavelength
5 - Cable Reactance Problems
6 - Impedance Conversion
7 - Coax And Audio
Conclusions
References
The coaxial cable was invented in 1929, but no-one could ever have known how popular it would become. Coax (as it's commonly known) is often thought of a being for radio frequency applications, but in reality a great many cables used in audio are also coaxial. The term itself simply means that the conductors share a common axis. There is a centre conductor, surrounded by an insulator, which in turn is wrapped in the second conductor called the shield. In almost all cases, there is a final outer insulating sheath over the shield to protect it from damage and corrosion.
In audio, we usually refer to such cables as being 'shielded', because it's very common to have two inner conductors (balanced microphone cables for example), and the term 'coax' doesn't really apply because the two inner conductors don't share a common axis as such. However, they are twisted together, and the twist is one of the reasons that these cables can reject noise that's external to the cable.
There are many RF (radio frequency) coax cables that can be used for audio, although there are many others that are completely unsuitable for a variety of reasons. For example, some use a single core for the centre conductor, often copper plated steel. This is fine for RF, because the skin effect means that the high frequency signal will be concentrated on the outer surface. Since the plating is copper, it has low resistance. The steel inner core gives the cable added mechanical strength, but it is not very flexible and cannot be bent to a small radius. If constantly flexed the centre conductor will break, so this type of cable is only suitable for fixed installations. However, it can be used for fixed audio installations if desired.
Other RF coax cables use a stranded inner conductor, most commonly 7 strands of copper, copper plated steel, tinned copper, silver plated steel and sometimes copper plated aluminium. Most RF coax cables are designated with an 'RG' (radio guide) number, such as RG-58, RG-174 etc., etc. While these designators are usually a passable indication of the specification of the cable, they are no longer completely reliable. If your application is critical, it's advisable to ensure that the cable meets the required standards. Simply selecting cable based solely on the RG number doesn't guarantee this.
In some catalogues you'll see cables referred to as (for example) 'RG-59 Type'. The word 'type' in this context means that the cable can be considered to have the basic characteristics of the cable that normally bears the number indicated, but there will be differences that may or may not be apparent. The impedance and outside diameter will usually be as expected, but many other things can be different, including the type of central conductor (solid or stranded for example).

Figure 1 shows the basic construction of a typical RF coaxial cable. Each of the sections shown can be changed depending on the intended usage. Many cables don't use a foil shield, and it usually cannot be used effectively for any cable that is intended to be flexible. In some cases, a metallised plastic is used instead of aluminium foil and that is more resistant to damage due to cable movement. The dielectric is the insulation around the centre conductor, and is a critical part of the cable.
At high frequencies, signals do not travel through a coaxial cable in the way you imagine. Once the length of the cable exceeds a significant fraction of the signal wavelength, coax acts as a transmission line. Rather than the movement of electrons, the signal is transferred as an electromagnetic wave. At much higher frequencies (microwaves), even coaxial cable may not be used - the signal is 'transmitted' along a hollow pipe called a waveguide. There is no centre conductor, and the waveguide's purpose is to contain the electromagnetic wave to (usually, but not always) one dimension - along the length of the waveguide from the source to the destination. An example is the waveguide used to carry the energy from the magnetron to the cooking chamber of a microwave oven.
With RF, you also need to be aware of the skin effect. This effect causes high frequency signals to concentrate on the outside of the conductor, and the inner section becomes (almost) irrelevant. Some HF coax for fixed installations will use an inner copper tube rather than twisted wires, because the centre part of the conductor serves no real purpose and isn't required. This saves weight and cost.
The skin effect can be circumvented by using Litz wire - multiple wires twisted together, but insulated from each other so the signal can't cross from one wire to another. If you wish to know more about the skin effect, look it up, because it isn't covered in detail here. Note that at audio frequencies, the skin effect has a very small overall effect on the conductivity of a cable, and it can safely be ignored. Skin depth is defined as the distance below the surface where the current density has fallen to 37% of its value at the surface. at frequencies up to 20kHz it can be measured, but you will rarely hear the difference (despite claims to the contrary by snake-oil vendors).
It's also important to understand that any cable has a characteristic impedance, not just coaxial types. Figure-8 ('zip' cable), twisted pair cables used for data transmission (Cat-5 for example), and even the aerial mains distribution cables (i.e. those on poles) - they all have an impedance that's based on the conductor size and spacing. At low frequencies (50 or 60Hz) the impedance is not a limitation unless the transmission lines are very long compared to wavelength. Consider that the wavelength at 50Hz is 4,800km or 4,000km for 60Hz (assuming a velocity factor of 0.8 - see below for more on that topic). Mains power transmission is a topic unto itself (and is very complex), and isn't considered here.
Another term that you will see along with 'coax' is 'transmission line'. All coax is a transmission line (at least at some frequency), but not all transmission lines are coaxial. A single PCB trace and a ground plane produce a transmission line, as do twisted pair cables and 'Figure-8' aka 'zip' cable. Most have no interactions at audio frequencies other than their intrinsic capacitance. At higher frequencies things can be very different, as discussed below.
Radio frequency coax always has a designated impedance, most commonly 50Ω or 75Ω. 50Ω coax is pretty much the standard for radio transmitters and receivers, laboratory equipment (for example almost all oscilloscopes are fitted with 50Ω BNC connectors). 50Ω coax matches the impedance of a quarter-wave 'monopole' (1/4 wave 'whip' or ground-plane) antenna. The use of 50Ω coax is indicated anywhere power needs to be transmitted, so most radio and TV broadcast systems will be 50Ω, as will mobile phone (cell phone) repeaters, CB and ham radio, Wi-Fi, etc.
75Ω coax is used for unbalanced TV antenna connections, satellite TV receiver systems, cable TV, broadband (cable) internet, video and S/PDIF digital audio. 75Ω is also a reasonable match for the impedance of a 1/2 wave dipole antenna (~70Ω) as used for many TV antennas. A transformer (balun) is needed to match coax to a 1/2 wave folded dipole antenna, as these have a nominal impedance of 300Ω (actually about 280Ω). 75Ω coax usually has slightly lower losses than 50Ω cables at higher radio frequencies.
Unlike cable used for mains or other power transfer, the impedance of a coaxial cable is not affected by its length. A 50Ω coax has an impedance of 50Ω whether it's one metre or one kilometre long. This doesn't mean that there are no losses though, and most cables are rated for their attenuation in dB per unit length. This varies with frequency, and all cables exhibit higher losses as the frequency increases. Power handling is affected in the same way, so the maximum power that can be transmitted is reduced with increasing frequency.
Don't expect to be able to measure impedance with a multimeter or similar, because the cable impedance is a complex mixture of primarily capacitance and inductance, with resistance (as measured by an ohm meter) having an almost insignificant effect. Of course, this doesn't mean that resistance doesn't matter, because it does. This is why many 75Ω coax cables use a copper-clad steel core for the centre conductor. The steel is cheap, but has high resistance, and the skin effect means that the HF signal will travel in the outer layer only - which is copper for improved conductivity.
The characteristic impedance of a cable is determined by a number of interdependent factors, including the ...
If the last two factors are known, the characteristic impedance (Z0) of a cable can be calculated by ...
Z0 = √( L / C ) Ohms
Where ...
L = inductance in Henrys
C = capacitance in Farads
As an example, if you have a cable that measures 100pF/ metre, it must have an inductance of 250nH/ metre if it's rated at 50Ω. This is easily verified by either rearranging the formula, or using those two values in the formula as shown. If you do that, the cable's impedance will work out to be 50Ω. You will also find that changing the length (and therefore the capacitance and inductance proportionally) doesn't affect the outcome - the impedance remains the same. 100 metres of the same cable will have a capacitance of 10nF and an inductance of 25µH, but the impedance is still 50Ω.
It's also worth noting that the above formula also works with twisted pair cables (as used for networking) and even side-by-side constructions such as 'figure 8' or 'zip cord' commonly used for wiring loudspeakers to amplifiers. Not that we need to care about the characteristic impedance of any audio cable, because the cable length is normally only ever a small fraction of a wavelength at the highest frequency of interest - 20kHz.
 | Note that as shown here, a cable has capacitance and inductance, so it is a tuned circuit. To prevent the tuned circuit from becoming a problem, there needs to be an impedance at least at one the end of the cable (preferably both) that matches the characteristic impedance of the cable. The capacitance and inductance are distributed along the length of the cable. |
To reduce the characteristic impedance of any cable, it's necessary to reduce the inductance and increase the capacitance for a unit length of the cable. Increasing the impedance naturally requires the opposite - more inductance and less capacitance. Very low impedance cables can cause audio amplifier instability because of the high capacitance, unless they are properly terminated (for example, by adding a Zobel network to the far end).
Cable impedance can also be calculated if you know the respective diameters of the inner and outer conductors and the dielectric constant (also called the relative permittivity) of the insulator around the centre conductor.
Z0 = 138 × log ( D / d ) / √εr Ω
Where ...
εr = Relative permittivity (dielectric constant) of the dielectric
D = Inside diameter of the outer conductor
d = Outside diameter of the inner conductor
The dielectric material is used to provide physical separation between the inner conductor and the shield. The material used should have stable electrical characteristics (dielectric constant and dissipation factor) across a broad frequency range. The most common materials used are polyethylene (PE), polypropylene (PP), fluorinated ethylene propylene (FEP), and polytetrafluoroethylene (PTFE, aka Teflon). PE and PP are common in applications that have lower cost, power and temperature range requirements (PE is 85°C, PP is 105°C). FEP and PTFE are for high power and temperature range applications (200°C), and have much greater resistance to environmental factors. However, they also cost a lot more.
The materials may be used in their natural (solid) form, or injected with gas bubbles to create a foam or cellular structure. This reduces both the dielectric constant and dielectric losses. Some rigid or semi-rigid 'cables' (intended for fixed installations only) use discs of insulating material spaced at intervals, so the dielectric is predominantly air, thereby reducing losses even further.
| Material | Relative Permittivity (εr) |
| Vacuum | 1 (by definition) |
| Air (sea level. 25°C) | 1.00059 |
| PTFE (Teflon) | 2.1 |
| Polyethylene | 2.25 |
| Polyimide (Kapton) | 3.4 |
| Polypropylene | 2.2–2.36 |
| Polystyrene | 2.4–2.7 |
| Polyvinyl Chloride (PVC) | 3.18 |
| polyethylene terephthalate (PET, Mylar) | 3.1 |
Some of the materials listed above may not be found in the cable itself. However, if you ever need to join a coaxial cable that's used at radio frequencies, be aware that 'ordinary' PVC insulation tape or Kapton tape both have a higher dielectric constant than the insulator materials normally used. This can cause an impedance discontinuity where the join is made. More consistent results will usually be obtained by using a dedicated cable joiner or a plug and socket with the same impedance as the cable.
A coaxial cable of a specific impedance is determined by the ratio of the dimensions, not the absolute values. A 50Ω coax can be as small as 2.5mm diameter or as big as 50mm diameter (or more). Provided the dimensional ratios are maintained, the cable impedance is also maintained. For example, assuming a dielectric constant of 2, a 50Ω coax has an outer to inner diameter ratio of 3.3:1 - it makes no difference if the dimensions are in millimetres, centimetres or inches, you will still get the same result. For a given impedance, the dimensional ratio is only changed if the dielectric constant is different.
Needless to say, there is a vast amount of information on-line. This includes impedance, capacitance and inductance calculators and many other tools that can be used to work out the characteristics of a given cable. However, the one piece of info you will almost certainly be unable to find is the relative permittivity of the dielectric, and this is essential before you can calculate the impedance or anything else. You can make an educated guess though, because most will be somewhere between 2 and 3 (see Table 1). If the material is 'foamed' (injected with air bubbles) relative permittivity will be reduced, but it may be next to impossible to find out the actual figure. If you can measure the dimensions accurately you can then work out the dielectric constant, assuming that you know the cable impedance (it's usually printed on the outer jacket or sheath).
One online calculator tool that seems to work well and gives expected results is Coaxial Cable Impedance Calculator. There are countless others, but I rather like this one because it provides everything you need with an easy to use interface.
(Note: There is no affiliation between ESP and Pasternack, and the link is provided purely as a service to readers.)
Something that tends to make the inexperienced really wonder about the overall sanity of electronics as a whole is a cable's velocity factor - an indication of how much the cable slows down an electromagnetic wave travelling in the cable. Sometimes it will be referred to as 'velocity of propagation' or similar, and it's normally expressed either as a percentage or a decimal fraction. A cable with a velocity factor of 0.75 or 75% means that the signal travels at 0.75 times the speed of light (in a vacuum), nominally 3 x 108 metres/ second (299,792,458 metres per second if you wish to be exact). For our example, the signal will travel at only 2.25 x 108 metres/ second - a significant reduction.
This means that it will take 5.6ns for the signal to travel along 1 metre of the cable, but it would only take 3.3ns for the same signal in a vacuum. It doesn't sound like much, but the velocity factor (VF) of a cable is critical with very high radio frequencies, and must be considered when designing some types of antenna (phased arrays for example). It's mostly a non-issue for audio of course, but it can still be a problem with very long lines (several kilometres up to many thousands of kilometres) as used in early telephony. Before fibre-optic cable became the standard for all overseas calls, submarine cables were used, and these were affected by the velocity factor of the cables.
If a signal has to travel from Sydney (Australia) to London (England) for example, that's a distance of 16,983km (as the crow flies). The delay is 75.5ms in a cable with a VF of 0.75 but is only 56ms at the velocity of light. None of this sounds like very much, but if telephone systems are not properly terminated (based on the characteristic impedance of the cables, including that from the exchange ('central office') to the subscriber, you get echo or reverberation effects that can make communication difficult. Note that not all of the delay is due to cable delays - there is always some latency (delay) in the processes of analogue to digital and digital to analogue conversion' ADCs and DACs - collectively known as CODECs (from coder-decoder). These all introduce delays, as does the switching equipment.
Velocity factor is mainly influenced by the relative permittivity of the cable's dielectric, but some other factors can also have an influence. In the early days of television, it was common to use a balanced 'twin-lead' (or alternatively 'ladder' or 'open wire' lines) between the antenna and the receiver. The common impedance used was 300Ω, and due to relatively wide spacing of the conductors, these cables had a velocity factor of up to 0.95 (95%).
As unlikely as it might seem, older 'high-end' oscilloscopes often used a length of coaxial cable as a delay line, coiled up in the case somewhere. The idea was that the signal would be fed directly to the triggering circuits, and a slightly delayed version (via the cable) then processed for the waveform display. This compensated for the short delay inherent in the trigger circuitry, and ensured a very clean trace without showing triggering artifacts - most commonly an apparent glitch at the beginning of the displayed trace. To this day, coax delay lines operate in many environments - anything from cellular phone base stations to airborne electronic warfare systems.
This is really a can of worms. There are so many different connectors that it's hard to know where to start. The first decision will always be the physical form of the connector, and it will usually have to mate with an existing connector on the equipment. It wouldn't make much sense to try to use a standard 1/4" (6.35mm) phone plug for an oscilloscope  . No suggestions are offered in this respect, simply because it almost always depends on the application and the equipment you have to connect to.
. No suggestions are offered in this respect, simply because it almost always depends on the application and the equipment you have to connect to.
Some connectors are available in only one impedance - either 50Ω or 75Ω. It is often important to use the exact type of cable that the connector is designed for - for example, you can't use a cable with a stranded inner conductor with an F-connector (as used for most modern TV installations, cable/ satellite TV, cable internet, etc.). These connectors only provide the outer shell - the centre conductor is simply extended into the connector body and forms the pin of the male plug. These connectors are designed to be used with RG-6/U or RG-59/U cable - note that there may be different versions to suit each cable type, because the cable outer diameters are often different. There may also be some variants of these cables that are the same size. See the comments above regarding coax cable designations - they aren't always reliable.
The characteristic impedance of a connector is determined by the dimensions of the inner and outer conductors, as well as the type of dielectric used to support the centre pin or socket. In other words, the impedance is worked out in exactly the same way as for cable. The F connector referred to above is a case in point, and it's designed to maintain the dimensions of the cable as closely as possible. This is surprisingly important - if the impedance of the connector is wrong, it causes a discontinuity that affects the signal by creating reflections. Every time the impedance changes, some of the incoming signal is reflected back to the source, and this reduces the level reaching the equipment.
Because of this, there is often a surprising amount of skill needed to terminate cables with connectors, since a discontinuity creates problems and loss of signal. Some connectors are much easier than others, and some require special tools or failure is almost guaranteed. The tools are often rather expensive, so only those who work with the connectors on a regular basis can justify the expense.
There is a staggering number of different types of connector designed for coaxial cable. All the major types have carefully controlled impedance (mainly 50 or 75Ω), and a small few are available in either impedance. BNC connectors are a good example - they are available in both 50 and 75Ω types. Many of the others are designed for a single impedance, and are not available with an alternative.
A few common examples include ...

| The RCA connector is listed above only because it's been used for many years for video cables (composite and RGB), which are designed for
75Ω. Unfortunately, RCA connectors are nowhere near 75Ω, and with the common types it's close to impossible to determine their impedance because
dimensions change through the length of the connector. There are some RCA connectors that claim to be 'true' 75Ω, but this may be rather optimistic for most.
Based on the dimensions (8.06mm outer shield, 3.12mm inner pin) and assuming an air dielectric, the impedance is about 56Ω. If a PVC or similar dielectric is used, that reduces the impedance to around 32Ω. In a domestic setup, RCA connectors usually work fine, but only because the cables are generally quite short compared to the wavelength of the highest frequencies encountered in the video signal. Since the short cable is not a transmission line, impedance matching isn't especially critical. |
This list is not exhaustive, and has been culled so that only the most common connectors are shown. There are a great many more, some of which have faded into obscurity, and others that are only used for very specific purposes (such as military or aerospace equipment). All the connectors listed (except the RCA) are primarily intended for radio frequency applications, but naturally they all work from DC upwards. Common use with audio frequencies is (generally) limited to only two of those listed - BNC and RCA. Not including connectors used for domestic TV (antenna and video, of which there are millions), the BNC is one of the most popular connectors of all time.
SMA connectors are gaining in popularity in recent years, as they are very compact, and have good performance at radio frequencies. They also perform well at audio frequencies of course, and as they use a screw thread on the locking ring, they can't easily be accidentally disconnected. Most are designed to use RG178 miniature coax
Almost every oscilloscope made since the early 1960s uses BNC female sockets on the front panel for all inputs (vertical, horizontal and sync). As a result of the proliferation of BNC connectors on oscilloscopes, other test equipment has also provided BNC inputs and outputs as well, so now almost all quality lab instruments will have BNC connectors as part of the instrument. If other connectors are needed, it's common to provide adaptors to mate with other equipment.
BNC connectors are also common for telecommunications, and were also used for early computer networking systems (ARCNET is one that I was very familiar with many years ago, and it survives to this day). Although the cable has an impedance of 93Ω (RG-62U), standard 50Ω BNC connectors were used. While this is a significant impedance mismatch, ARCNET cables could still be run for over 600 metres from an active hub to an end node, compared to ~180 metres for so-called 'thin Ethernet' aka 10BASE2 using RG-58 coax. This also used BNC connectors, as did other coax based networking schemes. A male line (cable) plug and chassis mount female socket are shown below.

It should be apparent that with so many different systems using BNC connectors, their reputation for reliability is second to none. The only time anyone will have issues is if exceptionally low quality connectors are sourced from Asia, and/ or the cables are badly terminated. Poor crimping (often because the wrong crimping tool has been used) and generally shoddy workmanship will cause problems, but it's surprising just how well even cheap connectors work ... provided you don't expect good performance up to several GHz of course.
It's also probably fairly apparent that I really like BNC connectors. So much so that even my workshop audio input (to amplifier and speaker system) and output (from FM tuner or CD player) are BNC, as are all my test instruments and various workshop preamps. Some adaptors are used, but most of the time I rely on BNC leads for almost everything. The majority have a BNC on one end, and alligator clips at the other with suitable flexible fly leads.
Most of my leads are RG-174U, a nice thin cable (2.55mm diameter) with a capacitance of around 100pF/ metre. It is not advisable to use leads of this type with an oscilloscope with a high-speed signal (such as a 10kHz squarewave), because they will affect the waveform far more than a x10 oscilloscope probe. For coupling audio bits and pieces together they are invaluable. Even 2.7 metre test leads only have a capacitance of 270pF. That can be enough to make a fast opamp oscillate, but a series 100Ω resistor will stop that, with no effect over the extended audio band (up to 100kHz).
For a (more-or-less) complete list of different coax cable types, see Wikipedia - Coax Cable. There are many that appear almost identical, and the 'RG' numbering system is not alone. Most of the cables in common use range from 2.5mm diameter (e.g. RG179) up to a bit over 7mm. The range and variety is extensive, with some designed for flexibility, and others of fixed installations.
This is a surprisingly complex topic, and even though there's quite a bit of info in this section, it's been simplified as far as possible to make it understandable. If this is a subject that you really need to understand fully, then you'll ideally get yourself some good books that cover the details thoroughly and (hopefully) accurately. While there's a lot of useful info on the Net, there's also a great deal that's either misleading or wrong. It can be very difficult to know which is which when you're starting out.
Unlike low frequency circuits which generally use low output impedances and high (or comparatively high) load impedances, with RF impedances need to be matched. This can also become necessary even with audio, but only if the cables are of significant length - typically several kilometres. The most common place that these conditions are found is in the telephone system.
With RF, it's not just the cables that form the transmission line - the connectors are very much a part of the overall circuit, as is any join in the cable or other transition from one medium to another. As such, the impedance of each part has to be carefully engineered to match the cable being used. This is the reason there is so much info on connectors in the previous section. Ignore these essential components at your peril, and remember that joints (and even small radius bends) need just as much attention.
When dealing with transmission lines, it's almost always necessary to know the wavelength. There are some seemingly very odd (but perfectly reasonable once understood) things that happen with high frequencies, and you will often need to know the wavelength to be able to make sense of the measured results. With low frequencies (such as audio) this is almost never a problem. Consider that the wavelength of a 20kHz signal is 15km for a signal travelling in a vacuum - it's even longer in a transmission line (twisted pair or coax). Increase the frequency to 100MHz and it's down to 3 metres. Wavelength is easily calculated ...
λ = v / f
Where ...
λ = wavelength (metres)
v = velocity of propagation (metres/ second)
f = frequency (Hz)
For the remainder of this section, we will assume a coax impedance of 50Ω, velocity factor of 0.75 (75%), and a frequency of 100MHz. It's quite easy to re-calculate everything described below for any frequency, and only basic maths (and a scientific calculator) are needed.
So, with a velocity factor of 0.75, the wavelength of 100MHz in the coax transmission line is 2.25 metres (using the above formula). If we have a source of 100MHz and feed it into a 2.25 metre length of coaxial cable, the signal at the unterminated far end of the cable will be reflected back to the source. This reflection will be in phase with the applied signal, and the cable appears to be open-circuit. The same thing happens if the cable is reduced to exactly 1/2 the length (1.125 metres).
Things become interesting (to put it mildly) if this same cable is a little over 560mm long - this is 1/4 wavelength (often referred to as a 'stub'). When a 100MHz signal is applied to one end, the unterminated cable appears to be a short circuit! The signal is reflected at the open end, but is now 180° out-of-phase. The reflection causes signal cancellation, and the source (such as a transmitter) will 'see' a short circuit and will probably be damaged. If the 560mm open stub is connected to a receiving antenna, it will filter out (remove) any signal at 100MHz, while letting adjacent frequencies through with little reduction. This is all very much frequency dependent, and all multiples of 1/4 wavelength will be affected in different ways, depending on the termination.
With a good quality low loss coax, the Q (quality factor) of this 1/4 wave trap is so high that the bandwidth may be as low as 100kHz, although expecting better than 1MHz is probably unwise. This is one place where the DC resistance of the centre conductor and shield dramatically affect performance. All cable resistance and dielectric loss appear in series with the coax tuned circuit, affecting the depth of the notch. Also, be aware that the signal will also be effectively shorted out at 300MHz, 500MHz, 700MHz, etc. This is known as a 1/4 wave stub, and as always you'll find plenty of information on line if you search for it.
Things get even more interesting if this same 560mm length of coax is now shorted at one end. It will appear to be a short circuit at DC (as expected), but it starts to show a significant impedance at a frequency of a little over 2MHz. At 100MHz (1/4 wave), it's now an open circuit, showing very high impedance - not quite infinite, but getting close. There will then be a series of peaks and nulls in the impedance curve, with the cable appearing to be open circuit at the same frequencies as above (300MHz, 500MHz, 700MHz, etc.). This type of 1/4 wave trap acts as a short circuit at 200MHz, 400MHz, 600MHz, etc.

In the above, you can see the transmission characteristics for a 1/4 wave stub, with the far end shorted (red) and open (green). The traces show the relative impedance seen from the source into the cable. The cable has a delay of 2.5ns, which is 1/4 wavelength at 100MHz. If we use the same cable referred to above (the one with a velocity factor of 0.75), a 1/4 wave stub will actually be 562.5mm in length (560mm is an approximation). This is both confusing and confronting when you come across it for the first time, because it seems to go against all logic, but it's all perfectly reasonable once you understand how it works.
From a little over 200kHz, the cable with the far end shorted (red trace) appears as an inductor. Its impedance increases with increasing frequency, until it appears to be an open circuit at 100MHz. The impedance then starts to fall, and is capacitive (falling with increasing frequency). At 200MHz the cable is a 1/2 wave stub, and it presents a short to the signal source. This process repeats as the frequency is increased further.
As may be becoming apparent, coaxial cable can be used for much more than simply a means for transporting a signal from one place to another. However, once the cable is terminated in its characteristic impedance, for all intents and purposes it disappears. The 1/4 wave stub discussed above simply becomes an almost perfect conductor when the load impedance and cable impedance are the same. Its only when the impedances are mismatched that problems (and apparently strange behaviour) arise.
We can take it from this that impedance matching is critical, but it's very important to understand that these effects to not come into play until the length of the cable is 'significant' compared to wavelength. A 'rule of thumb' that can be applied here is that significant means an order of magnitude - for the example shown above, effects become noticeable at 10MHz - 1/10th of the frequency we are working with.
Most people working with audio will never experience any of the phenomena described, because the cables needed to experiment are simply far too long if you are limited to the audio range. Even if you can generate a 1MHz signal (and somehow consider it to be 'audio'), you're still looking at a 1/4 wave cable that's around 56 metres in length, so it's not easy to verify if you don't have the ability to generate (and measure) high frequency signals. At 100kHz, you need over 500m (1/2 a kilometre) of cable. Unwieldy and expensive to put it mildly.
At any frequency below around 10MHz, the length of coax we've used here is classified as being electrically 'short', because the line length is much less than a wavelength. The impedance seen by the source is almost entirely dependent on the load impedance at the far end of the cable. It follows that for audio (and even well above), this is a 'short' line, and it never behaves like a transmission line - it's simply a cable with resistance, capacitance and inductance. A piece of wire!
Once the cable length is several wavelengths, it is an electrically 'long' line. The load seen by the source now depends primarily on the cable. Provided the load impedance equals the characteristic impedance of the cable (e.g. 50Ω), the source sees only the cable impedance. In an infinitely long transmission line, the impedance seen by the source depends solely on the cable. This is because it will take an infinite amount of time for the original signal to reach the end of the cable, so the load is irrelevant.
In the real world, it's often hard to ensure that a radio frequency load (an antenna for example) is exactly the right impedance. We now know that if the load doesn't exactly equal the cable impedance there will be reflections, and these are easily measured with fairly simple test instruments. The most common of these is the VSWR meter (sometimes referred to as SWR). VSWR stands for 'voltage standing wave ratio', and this is a good measure of the impedance mismatch between the cable and load. If both impedances are equal, the VSWR is 1:1 (unity) - this is the ideal case.
VSWR = ( 1 + Γ ) / ( 1 - Γ ) or ...
VSWR = Vr / Vf
Where ...
VSWR = voltage standing wave ratio
Γ = reflection coefficient (Gamma) - ( √ Reflected Power / Input Power )
Vr = Complex value of reflected voltage
Vf = Complex value of forward voltage
VSWR is essentially a measure of how much of the delivered power is reflected by the far end of the transmission line - coaxial cable in our case. If we deliver 10W to a cable and load (typically an antenna) and 2.5 watts are reflected due to an impedance mismatch, the measured VSWR is 3:1 (or just 3). In this case, the gamma (Γ) is 0.5 as shown for the formula notes.
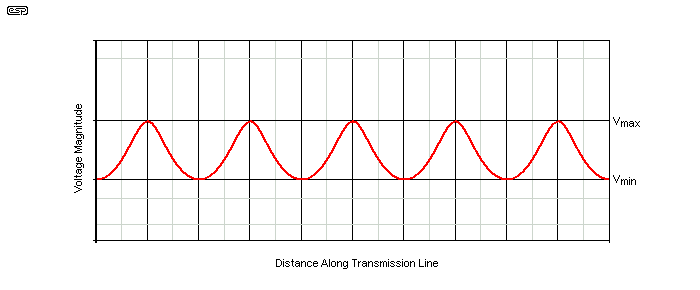
Figure 4 - Voltage Measured Along A Transmission Line
In the above, you can see that the voltage varies between a maximum and minimum along the length of the line. This is the voltage standing wave ratio, and for the above, a 50Ω cable was terminated with a 100Ω resistor (representing the load - typically an antenna). This provides a VSWR of 2:1 due to the mismatch. VSWR meters are designed to match the impedance of the system they will be used to test, and since most transmitters use 50Ω, so are the meters used. Naturally, for 75Ω systems a 75Ω VSWR meter must be used.
In many cases, the VSWR will be determined by a different measure - return loss, expressed in dB. A VSWR of 3:1 is equivalent to a return loss of 6dB. The ideal return loss (RL) is infinity, which indicates that there is zero loss and the impedances are exactly equal. With RF systems, it's unrealistic to expect better than 30dB, indicating a VSWR of 1.065:1 and a reflection coefficient of 0.032. There are several useful converters on the Net - one that I used for this article is VSWR to return loss conversion.
RL = 10 × log ( P1 / P2 ) or ...
RL = 20 × log ( V1 / V2 )
Where ...
RL = return loss
P1 = forward (input) power
P2 = reverse (reflected) power
V1 = maximum voltage
V2 = minimum voltage
Return loss is always used in telecommunications systems rather than VSWR, and it's measured using a return loss bridge. An example of a return loss bridge is shown in AN-010 - 2-4 Wire Converters / Hybrids on the ESP site. This is specifically related to telecommunications systems, where return loss has been the measure for impedance matching for many years (VSWR is not used). Note that return loss should always be expressed as a positive value, although in some cases you may see it (incorrectly) expressed as a negative.
It's interesting to see a length of coax along with the signal wave, and this is shown below. Only a single cycle is shown, having three nodes (zero voltage points) and two antinodes (peak voltage points). If a short circuit is placed at a node, it's 'invisible' to the source, which sees an open circuit. Conversely, if the node is open, it will be seen as a short by the source. This seemingly odd behaviour may be unexpected, but it happens whether you like it or not. Of course, the wave isn't a static entity as shown in the drawing. From the source, it varies from zero, through the positive peak, back to zero, then the negative peak, repeated indefinitely.
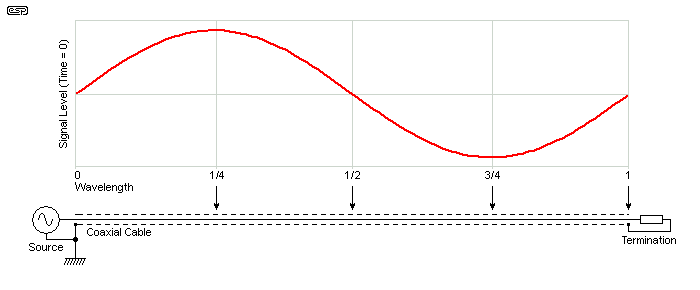
An open circuit antinode appears to be a short to the source, and naturally if it's shorted, it appears as open circuit. These conditions can only exist at frequencies where the length of the cable is a perfect multiple (or sub-multiple, i.e. 1/4, 1/2, 3/4) of the wavelength, so the short vs. open conditions only apply at specific frequencies. At other frequencies, the cable is a complex impedance creating a tuned circuit, but since it's only resonant at very specific frequencies determined by its length, other nearby frequencies are relatively unaffected.
This can all be quite difficult to come to grips with, and isn't easily explained in simple terms. However (and with any luck), the explanations here will be helpful to your understanding. Don't worry too much if it doesn't seem to make sense, because we are talking about RF after all. 
Provided you use reasonably well matched impedances with coax, you will generally get fairly good results with RF applications. However, impedance matching is (almost) never used with audio, and that can introduce some apparently strange behaviour with some circuits.
From the info shown above, it is (or should be) quite obvious that a coax cable isn't just 'a piece of shielded wire', but is something far more complex. Indeed, even a piece of shielded wire isn't just 'a piece of shielded wire' - it's a coaxial cable. Anyone who has looked through the various ESP projects will have noticed that I always include a 100Ω resistor at the output of any preamp or other circuit that is likely to be connected to other gear with a cable. This can be thought of as a 'stopper' resistor, in that it stops the output circuit from interacting with potentially very low impedances at specific frequencies determined by the characteristics of the attached cable.
Because the cable between pieces of equipment will nearly always be shielded, that means it has capacitance and inductance and is therefore a resonant circuit. More importantly, it is a transmission line for high frequencies. The reactance of the cable doesn't create a problem within the audio band, but it does cause issues within the bandwidth of the opamp (whether integrated or discrete). The cable is perfectly capable of causing an opamp to oscillate, often at a frequency that's outside the bandwidth of many budget oscilloscopes. That means that even if it does happen, you probably won't even be able to see it on the scope.
The inductance of the coax (for audio applications) is almost never a problem. However, the capacitance is often right in the range where opamps (and even emitter followers) are subject to the greatest potential for oscillation. Few active circuits like capacitive loads, and the most critical range is from around 500pF up to 10nF or so. This is exactly the range of capacitance that common shielded cables and/or 'true' coax will present to the driving circuit. Very short lengths (as used for internal wiring for example) are usually below the critical range, but 'typical' interconnects will usually measure somewhere between 500pF up to a few nF, and will cause problems if an output 'stopper' resistor isn't used. Some opamps are less tolerant than others, and the datasheet may (or may not) indicate the response with capacitive loading. Few opamps can tolerate a capacitive load of more than ~200pF without 'bad' things happening (some can tolerate a great deal less - for example, the LM833 may oscillate with a capacitive load of more than 50pF).
If an opamp oscillates at some extreme frequency, the effect is often audible as either hum or buzz, it may cause audible distortion, or it may have no audible effect - until you use a different cable. It's completely unpredictable, and never good. Adding a series output resistor is enough to swamp the effect of the cable, by isolating the opamp's output from the external high Q resonant circuit that is the cable. Even a simple emitter follower can be affected, and it's worse if the base is fed from an impedance that is low at high frequencies.
While I use a 100Ω output resistor as a matter of convenience, in some cases the series output resistor can be reduced. It's rarely necessary though, because most other audio equipment has an impedance of at least 10k, and usually more. The attenuation caused by the 100Ω resistor is negligible, and I have never seen any opamp oscillate with any cable when the resistor is used. However, I've seen many discrete and opamp based amplifiers oscillate if the resistor is omitted - even as little as a 1 metre cable can cause oscillation in some cases. The following is an example, taken from Project 88 (left channel output stage). The output will generally be connected to a power amp (or perhaps an electronic crossover) via a shielded cable, and R9L is the output resistor.
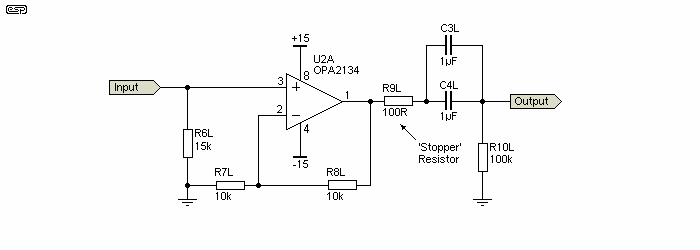
There are other ways of preventing any oscillation problems caused by a coax cable, but most are more expensive, less convenient, or both. You can use a Zobel network at the far end - i.e. the equipment being supplied with the signal. I don't know of any manufacturer of audio equipment that includes a Zobel network at the inputs, so it would have to be added (a 51Ω resistor and a 220pF cap in series would work). Other than modifying equipment, this is not a viable solution - especially since the solution is so cheap and simple. With power amplifiers, it's common to include a 10Ω/ 100nF Zobel network and an RF 'choke' (inductor) of a few micro-Henrys at the amp's output to prevent problems caused by speaker cable capacitance. The same thing can be done with preamps, but a resistor is a far simpler option, and works just as well.
Over the years, many people have asked me why the 100Ω resistor is included, and now you know the reason.
In some cases, you might find that a circuit just doesn't sound 'right', with audible artifacts or some other issue that indicates that there's a problem. In some cases, you can probe around with a finger (provided there are no high voltages present of course), and you might find that if you place your finger 'there', the problem goes away. This is almost always a good indicator that there is high frequency oscillation within the circuit, and your finger provides just enough coupling/ decoupling/ damping to stop or reduce the level of the oscillation. This usually means that you need a re-design of the board, but in some cases you may be able to include a series output resistor and/or a low value cap in the feedback network, or just use a different opamp. Some opamps are way too fast for audio, and there are a few that like to oscillate (at RF of course) - the LM833 is one that I know that would sometimes rather oscillate than amplify.
Impedance conversion requires a transformer, which may also be required to convert from balanced to unbalanced. This is needed with a 1/2 wave folded dipole antenna for example, and has to convert a balanced 280Ω (300Ω is generally assumed) antenna impedance to 75Ω unbalanced. The term 'balun' is simply a contraction of balanced-unbalanced, and they are very common with TV and FM receiving antenna installations. In most installations, a balun will be used to connect a balanced antenna to an unbalanced feeder - a coax transmission line leading to the receiver (or transmitter).
Because the frequencies used for TV and FM are fairly high (over 80MHz for nearly all systems now), the transformer is fairly simple, and for receiving systems is normally just a few turns of insulated wire through a ferrite bead. There are countless ways to make baluns, and it's worth doing an image search to see the different types that can be made or purchased. A common TV balun may use perhaps 6 to 8 turns on the 300Ω side, and exactly half the number for the other winding. Not all baluns are isolating, so some will use a single tapped coil (an autotransformer) rather than separate windings.
Baluns are also sometimes used in reverse - converting a balanced transmission line to an unbalanced load, but this is less common. The inductance needed is very small - as little as 10µH is usually more than sufficient for frequencies above around 50MHz. However, this article has no intention to cover the design of RF transformers or baluns - it is a general discussion only.
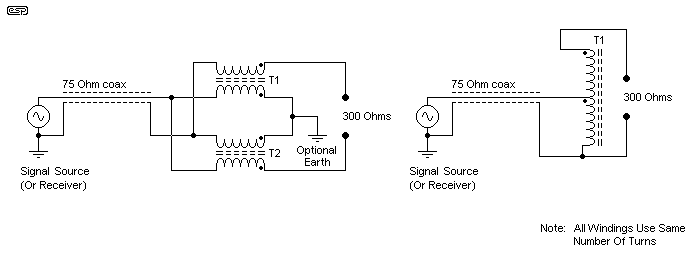
A couple of more-or-less typical designs are shown above. The single auto-transformer version is not a true balun, because both input and output are unbalanced. However, if it's connected to a folded dipole antenna that doesn't have an earth connection at the mid-point of the dipole itself it will still work fine. Most TV and FM antennas do earth the centre point of the dipole though, as this provides some protection against nearby lightning strikes. However, protection circuits notwithstanding, a direct hit will usually destroy everything regardless.
There's an old myth that says "lightning never strikes the same place twice" - generally untrue, but it can arise simply because the same place isn't there any more! 
It's important to understand that many RF circuits are as much an art as they are a science. Some of the most unlikely circuits can be seen in RF installations, and the apparently simple act of impedance conversion can become anything but simple when you have a 500kW transmitter to deal with. A seemingly insignificant resistance or impedance variation can become your worst nightmare very quickly, since the transmitter will have an output of 5kV at 100A for a 50Ω system. They are quite scary numbers, and if the transmission line only loses 10% of the input power it has to dissipate 5kW - that's a lot of watts!
With the introduction of digital TV, transmitter power is generally lower than was the case with analogue transmissions, but they (mostly) operate at higher frequencies. However, in some parts of Australia digital TV transmitters have an effective radiated power (ERP) of up to 350kW. Effective radiated power is a measure of the transmitter's actual output and the gain of the antenna system. A detailed discussion of this is well outside the scope of this article.
Coaxial cables are common in audio, but are generally referred to as 'shielded cables'. This is simply because the characteristic impedance is usually uncontrolled, and is not relevant. Even with a velocity factor of 0.66, the wavelength at 20kHz is 9.9km (yes, kilometres). These are uncommon in home installations, where the leads are typically no more than a couple of metres in length. Since it's already been established that any coax that's shorter than λ/10 is not acting as a transmission line, as long as your signal leads are less than a kilometre you don't need to be concerned about impedance matching. Note however, that this does not apply to cables handling video!
For audio, only one thing matters ... capacitance. One of my favourite cables for internal wiring (and test leads) is RG174/U, a flexible 50Ω coax that's only 2.5mm diameter. Another is RG316/U which is (IMO) a better cable, but harder to find and more expensive. The capacitance of both is about 100pF per metre, so even if driven by a 10k source impedance (uncharacteristically high, but a good example), the signal will be attenuated by 3dB at 159kHz with a 1m cable. This will naturally not cause any audible degradation. Most connections are far shorter, and are driven with a lower resistance.
As noted earlier, many opamps (and discrete circuits including simple emitter followers) will oscillate if their bandwidth is high enough to reach the resonant frequency of the length of coax connected to the output. If you have 1-metre shielded cables (coax), the resonant (full-wave) frequency will be somewhere between 100-300MHz, depending on the coax itself. Should an active device be connected without a series damping resistor (I use 100Ω), there is a good chance that the circuit will oscillate. This chance is increased if the 1/4 wavelength (25MHz to 75MHz) becomes 'excited' by the coax, and that's well within the bandwidth of many modern devices.
However, it's not even necessary to 'excite' a length of coaxial cable, and capacitance alone is often all that's needed to trigger oscillation. Many opamp specifications show the maximum permitted capacitive loading before the device becomes unstable. For example, the NE5532 opamp has a unity gain bandwidth of 10MHz, loaded with 600Ω in parallel with 100pF. The datasheet doesn't say what the maximum capacitance is, but You can be pretty sure that more than 100pF would be ... inadvisable.
You can see the trend with a simulator, but the models used in most aren't good enough to predict instability at this level. What you can do is run a frequency sweep up to at least 10MHz with a known working circuit, and you'll usually see a peak occur at some high frequency. For example, a SIMetrix simulation with a TL072 shows a peak of over 5dB at 623kHz (and no, I don't believe that at all). However, the trend will be seen, and doubly so if you build the circuit and test it. Often, you'll find that the oscillation is parasitic, and only shows up at certain points on the output waveform. This is easily confirmed by testing the circuit.
Provided you always use an output damping resistor from opamp or discrete circuit outputs, it's highly unlikely that cable-induced oscillation will ever cause a problem. If you don't then the results will be unpredictable at best, unusable at worst. The simple addition of the output resistor ensures you will have no problems (at least from output loading). Poor PCB layout and/ or lack of adequate bypassing can, and do, cause apparently very similar problems. However, the causes are quite different, and are not related (other than by accident).
By nature, RF is somewhat sneaky. Although radio frequencies really do obey all the laws of physics, to the casual observer this isn't always apparent. Coaxial cables and/or transmission lines are the case in point here, and as should now be obvious they are far more complex than they seem. Impedance is a critical factor once coaxial cable is used at a frequency where the cable is long (or 'significant') compared to wavelength.
In this context, a cable's length has to be considered significant once it is longer than about 1/10th of the signal wavelength at the highest frequency of interest. If you are only dealing with audio frequencies (including up to 100kHz or so), the cable makes little or no difference unless it's more than 300 metres in length. This is rather unusual in most cases, so it's safe to regard any coax (including shielded audio cables) as simply being a piece of wire that has a shield wrapped around it. As such, you need to consider the cable's capacitance, because that will work with the equipment's output impedance to create a low-pass filter. Impedance of most audio cables is irrelevant, and if anyone tries to tell you any different be wary - they may be trying to sell you some expensive snake-oil.
A 30m long piece of coax with a capacitance of 100pF/m (a reasonable value for many cables) has a total capacitance of 3nF, so to get response to 100kHz (-3dB) means that the equipment's output impedance has to be no more than 500Ω. If you need to be able to transmit a digital signal at 100kHz (which is a pulse waveform, essentially rectangular), the cable must be terminated with the correct impedance or the waveform will be distorted by the reflections of the high frequency harmonics. In the worst case this will make the data unreadable, but if marginal it will cause errors and make the connection slower.
Most modern computers operate at speeds where digital buses need to be terminated or the data will be severely degraded. If a data bus is bidirectional, a terminator will usually be located at each end of the bus. Computer bus termination can be passive (just a resistor) or active, using circuits designed for the purpose. The PCB tracks form transmission lines for high speed data, and these are affected by every issue noted in this article. There is some more detail on this topic in the article Analogue vs Digital - Does 'Digital' Really Exist?.
The interactions between high frequency signals and transmission lines of all kinds are very difficult areas to understand, and engineering at this level is very different from that needed for audio, industrial processes and most other areas where electronics is used. As data speeds increase, most digital system designers have to be aware of the limitations of their PCBs, interconnects and other wiring.
Hopefully, this article has cleared up at least some misconceptions about shielded cables (coax) in general. Remember that all shielded cables are equally affected, regardless of whether they are specifically intended for RF applications or not. Shielded audio cables are still coaxial, but their impedance is undefined. Due to their intended purpose (audio), they may have a lower Q than RF coax, but are still more than happy to cause a circuit to oscillate if precautions aren't taken. Dual conductor shielded mic cables will also share many of the characteristics of a 'true' coax cable, but the inner twisted pair causes some changes to their operation. Despite this, they can (and will) still become resonant circuits at radio frequencies.
 Main Index Main Index
 Articles Index Articles Index
|