

|
| Elliott Sound Products | Valve (Vacuum Tube) Preamps |
 Main Index
Main Index
 Valves Index
Valves Index
Before reading this article, I suggest that you read Bias and Gain, as that provides a lot of the background that is needed here. Although may points are repeated here as needed, the concepts of bias and gain need to be well understood before we look more closely at the many things that seem to conspire against us.
Valve preamps are essentially very simple, so much so that it's actually hard to make one that doesn't work. To get the optimum performance from valves is actually quite difficult though, and often for reasons that are very baffling until you know the cause. Even then, the very characteristics of valves themselves are constantly working against you - the relatively low gain and high intrinsic impedance of valves are sources of constant battles to get the desired end result.
This is one of the issues that made the uptake of transistors so dramatic once they became affordable. Of course, transistors also have intrinsic impedances that require extensive work-arounds to get good results, but most modern designers are far more comfortable with semiconductors because they are a little less mysterious in many respects. There is no doubt that very good results can be obtained from valve circuits, and many of the common circuit designs we see today stem from original designs that used valves as their basis.
Differential amplifiers (aka long-tailed pairs), the Schmitt trigger, cascode circuits and many of the standard RF oscillator configurations were all originally designed using valves, and only much later transferred to transistor circuitry and then into ICs. Even logic gates, dividers and other essentially digital circuitry were all pioneered using vacuum tubes.
This article is devoted to low-level circuitry, and how to minimise the problems encountered due to the high impedances and low gain of typical valves. All examples here are limited to the most common valve types used in preamps, namely the 12AX7 and 12AU7. There are many others, some of which are superior to those I'll be using, but they are less common, more expensive, and I don't have any to hand for testing.
One thing I will not include here is a complete valve preamp design, nor will I attempt a valve RIAA equalisation (vinyl disc) circuit. There are countless designs on the Net, but all of them are well below the performance of the ESP P06 phono equaliser. I do understand that many people like the full retro approach, but there are simply some things for which valves are fundamentally inappropriate, and RIAA equalisation is one of those.
A common claim is that a valve preamp (for example) is far simpler than a transistor equivalent. This is true only if you completely ignore the power supply. Although it is superficially simple, the high voltage parts needed are dramatically more expensive than the low voltage components needed for a transistor or IC preamp, and you still have to mess around to get the proper heater voltage. Then there's the added expense of finding decent valve sockets and, of course, the valves themselves.
Many resistors in valve amps have relatively high voltages across them and are also relatively high values, and that leads to excess noise and reduced reliability in some cases. Silly comments about transistor circuits needing high value (electrolytic) capacitors are a distraction and don't reflect reality. The cathode resistor in most valve circuits needs an electrolytic bypass capacitor too, and that's subjected to high temperatures that don't occur in transistorised preamps.
The following short section is duplicated in the Valve Vs. Transistors article that discusses the difference between valves and transistors. There is also some information in the Valve Myths article that shows the results of a direct comparison between valve and transistor stages, and shows conclusively that even a simple one-transistor stage can beat a valve stage for both noise and distortion.
It's worth noting that there have been several 'studies' published by electronics professional organisations, and while the results might appear to show that valves are 'superior', the results have to be taken with a very large pinch of salt. For example, an article on the IEEE website entitled "The Cool Sound of Tubes" is seriously flawed and simply shows the bias of the author. The article was published in 1998, and many of the claims made regarding noise and distortion simply don't stand up to scrutiny. In some cases, noise is measured with resistance in series with the input, so the thermal noise of the resistor itself is a major limiting factor. Comparing a triode with a single transistor circuit is somewhat unfair, because other than a few very early designs, this is not how transistors are generally used. It is notable that several opinions are provided, but they are nearly all from designers of valve equipment, with nary a word from respected designers who work primarily with semiconductor devices.
Another study from 1972 and published by the AES ("Tubes vs Transistors: Is there an audible difference?") is hardly worthwhile today, because so much has changed in the 40+ years since the article was written. It doesn't help that the writer's bias is clearly obvious, and that some of the claims made are best described as alarming! Of even more concern is the fact that there is zero reference anywhere to proper double-blind subjective testing, and that means that the published 'results' are worse than useless.
A comparison table of advantages and disadvantages of valves and transistors presented is laughable. Many of the comparisons fail to mention valve failings that are highlighted as 'disadvantages' of transistors, do not include a similar disadvantage (which exists as a matter of physical principles) of valves. For example, the stored change of transistors is listed as a disadvantage, but the equivalent problem of electron transit time through a valve escapes mention. Ok, so it's not a major problem, but limited high frequency response due to anode-grid capacitance wasn't mentioned, nor was the inductance of the internal lead wires (although this is not an issue with audio frequencies). Some of the other comparisons simply defy reason, such as transistors have "Usually more physical ruggedness than tubes (depends on chassis construction)". What unmitigated drivel - the chassis has nothing to do with anything, and needless to say wasn't mentioned for valve circuits where it's far more important.
It can be taken as read that these articles (and many more like them) are treated as gospel by those who imagine that valves are better, more linear, more musical (etc., etc.) than transistor or IC designs. They will regard anything that supports their view as 'proof' that they are right. There's no need to be objective and do your own double-blind tests when the proof you are looking for is all over the Net. Having your beliefs crushed is painful, and it's much better all round to disregard any evidence that you find confronting.
Before we start, it's important to understand what a valve does, and (at least on a theoretical level) what happens when something changes. A valve is a voltage to current converter - a voltage applied at the grid causes a current to flow in the plate circuit ... provided of course that the plate circuit is connected to a positive potential with respect to the cathode. In order to emit electrons efficiently, the cathode is heated, and coated with various materials that were found to emit electrons at lower temperatures than would otherwise be the case.
For the purposes of this article, only indirectly heated cathode valves will be considered. In this arrangement, the cathode is a metal tube, and the filament (now called a heater) is installed inside the tube, with an insulating coating to the two cannot make contact.
There are several parameters that are always provided in valve datasheets, and these are necessary for the user to work out how the valve will perform in a real circuit. The most fundamental of these is the amplification factor - µ (pronounced mu). This is the maximum theoretical gain the valve can provide, and in a perfect world would be independent of voltage or current. In the real world, this does not apply.
The second major parameter is the internal plate resistance (rP) - the effective internal resistance of the valve itself. This is derived by measuring the change of current flowing through the plate circuit for a known change of voltage across the valve, with the grid voltage held constant. Plate resistance is then determined using Ohm's law ( R = V / I ). So if the plate voltage is changed by 10V and the current varies by 250uA, the resistance is 40,000 ohms (40k).
The last of the dynamic properties is mutual conductance (gm - 'gee-em'). This may be described in µmhos (the mho is the inverse of the ohm, so is conductance as opposed to resistance). Other terms are Siemens (1S = 1 mho) or - and preferably - mA / V. The last term is almost self explanatory - the plate voltage is held constant, and the current change measured for a known change of grid voltage. If a 100mV change on the grid causes a 0.5mA change in plate current, the gm is simply 0.5mA / 0.1V = 5mA / V.
Amplification factor is generally derived from rP and gm, based on the formula ...
µ = gm × rP
In the same perfect world that we didn't have before (and still don't), all of these functions would be linear, and would remain so provided we stayed within the limits for a particular device. Needless to say, this is not the case, and non-linearities abound. It is these very non-linearities that we must confront in order to design a workable circuit with the required parameters - in particular frequency response and distortion.
The biggest problem with valve circuits in general is impedance - high impedance to be specific. Apart from inevitable high frequency loss which comes free with high impedance circuits, the high resistance values mean that thermal noise is higher than we might prefer, and electrostatic fields can cause hum problems. Valves used in preamps can be microphonic, so they pick up vibration which is often injected into the circuitry. Once there, it cannot be removed, and the audible effects are dependent on many different factors. Audibility can range from severe to nil, and is affected by proximity to loudspeakers, room geometry, etc., etc.
There are quite a few rules of thumb that were common knowledge during the valve era, but many of these are lost unless one has access to books about valves, written when valve designs were at their peak. Chief amongst these for me is the Radiotron Designer's Handbook (1957 edition), which is highly regarded and generally considered to be one of the most comprehensive books about valves ever written. Naturally, it's also important to be able to make and test actual circuits - while the theory is fairly important, in many areas the calculations that one can make are cumbersome, tedious, and have limited accuracy unless you are 100% certain that the valve you are using is identical to the typical data published. With reliable valve supply an uncertainty at the best of times nowadays, the chances are low that the valve you are using will be exactly as described.
The rules that were generally applied back then are nearly all to do with impedance, since this is the parameter that affects the way a valve performs. There will always be occasions where the rules are broken to obtain a specific result, but in general they were devised to maximise bandwidth and minimise distortion. Even at low levels (a few volts at most), valves can introduce considerable distortion. Other than for instrument use (especially electric guitar), distortion is never beneficial. A relatively benign 2% THD (total harmonic distortion) that is predominantly 2nd harmonic can introduce a great deal more intermodulation distortion than is expected or desirable.
The basic rules used are (or were) ...
Rule 1
Of these rules, the first is the most commonly violated, because it is assumed that the grid circuit of a valve is virtually infinite provided the grid is negative with respect to the cathode. This is true only up to a point. As the input signal drives the grid positive, the negative grid-cathode voltage is reduced, the valve draws more current and the plate swings negative from its quiescent voltage.
What also happens is that the grid starts to draw a small current (sometimes referred to 'grid damping'). Provided the source impedance is low, the extra current is immaterial, and causes no problems. When the source impedance is high, the tiny grid current drawn as it approaches the cathode voltage loads the source more. A stage with a nominal input impedance of 1M (no signal, and set by the grid resistor) will be very close to 1M, and it will remain so for negative input voltage swings. Positive input swings naturally reduce the grid-cathode voltage, and the grid current starts to rise. The point where this occurs depends on the valve type and anode voltage, and is not normally supplied in datasheets.
For the sake of explanation, assume that the cathode is at +1.5V, so the grid is at -1.5V with respect to the cathode, via a 1M resistor. Grid current may be a few nanoamperes and can be disregarded. A negative input voltage of say 1V makes the grid more negative (-2.5V WRT the cathode), turning off the electron flow, and grid current may fall even further. Because the process is far from linear, a positive 1V signal will reduce the grid-cathode voltage to 0.5V, and grid current might rise to 500nA (as an example only).
This seemingly minuscule amount of current will have absolutely no effect on a low impedance source, such as a signal generator (for testing) or a CD player (for listening). The valve's input impedance changes, but over such a tiny amount that a low impedance source is unaffected. We need to calculate the impedance change now, because this is crux of the problem.
Nominal impedance is 1M, but this is in parallel with the valve grid, drawing virtually no grid current, so we'll ignore it. With a negative voltage swings the current (if any) is reduced further, so can be ignored even more.
If you're still following this, we're doing alright. 
The fun part comes about when the grid swings positive. With a 1V positive swing, grid-cathode voltage is 0.5V, and grid current may rise to 500nA, so the valve's input impedance is 0.5V / 500nA = 1M. This is in parallel with the grid resistor, so total impedance is 1M || 1M = 500kΩ We can't ignore that! This means that the impedance is different for positive and negative signals, and becomes worse as signal level increases. If the source happens to be high impedance (1M perhaps) it will be loaded differently depending on the polarity and the amplitude. The result is distortion, and that's before the valve has even attempted to amplify anything.
This is real, and can be tested easily by driving a valve preamp circuit with a high impedance. I have done the test, and was easily able to increase total distortion from 2% to 5% for the same RMS output voltage, just by adding a series resistance between my signal generator and the preamp circuit. (I used 220k.)
Rules 2 & 3
Normally, to get the maximum gain from any valve, the plate load resistor has to be as high as possible. Mu (µ) or amplification factor, is the maximum voltage gain possible, but is only possible with an infinite plate load resistor (which requires an infinite plate supply voltage). A good current source will get very close, but valves are not good enough - you'll need to use a high gain bipolar transistor.
In reality, the plate load resistor is a compromise, but 100k is a common value for 12AX7 valves. Plate resistance depends on plate voltage, and for 100V on the plate, rP is around 80k - according to the data sheet. Since µ is 100, the voltage gain with a 100k plate load is about 55. (How this is determined will be looked at later, but the details are also in the Bias and Gain article.) We also have a circuit of some kind after the amplifying valve, and unless it happens to be a cathode follower, the impedance of the following load is in parallel with the plate load. If we apply Rule 3, the minimum is 400k (4 x RP). The total load on the valve is now 80k, so the gain is reduced to 50.
The upper and lower frequencies that a preamp can reproduce are determined by resistance (or impedance) and capacitance. For low frequencies, the value of the cathode bypass capacitor should be between 5 and 10 times larger than needed for a desired low frequency response. This ensures that the (usually) electrolytic capacitor is not part of any high pass filter that is created by coupling capacitors and circuit impedances. Electros can generate considerable distortion when their reactance becomes significant - at the frequency where capacitive reactance equals the value of the cathode resistor.
To calculate the value of any coupling or bypass capacitor, the standard formula is used ...
C = 1 / ( 2π × f × R ) (Where f is the lowest frequency of interest, and R is the resistance of the grid or cathode resistor)
For cathode bypass caps, the value obtained from the above should be multiplied by 10. For example, for a 1.2k cathode resistor and a minimum frequency of 20Hz, the cap needs to be ...
C = 1 / ( 2π × 20 × 1,200 ) = 6.6µF × 10 (use 100µF)
As shown, the sensible choice here would be to use a 100µF cap with a suggested voltage rating of 10V. Since it's in a valve amplifier, a 105°C temperature rating is strongly recommended.
Where a capacitor is used to couple two stages, the total series resistance is really the output impedance of the driving stage plus the grid resistance of the driven stage. It's generally easier to disregard the source impedance unless a strictly defined lower frequency limit is required, but if this is the case it's better to use an active filter. Remember that if multiple stages are cascaded, the rolloff frequency will be increased, so allowance must be made for the number of stages. For a single stage driving an impedance of (say) 100k with a -3dB frequency of 20Hz, the cap value is ...
C = 1 / ( 2π × 20 × 100k ) = 79nF (Use 82nF or 100nF)
To determine the high frequency response, you'll need to consult the datasheet for the valve you are using. The most significant value is the plate to grid capacitance, and this is multiplied by the stage gain. For a 12AU7, this is 1.5pF, and if the stage has a gain of (say) 10, the capacitance (CMiller) becomes 15pF.
To calculate the HF response, you need to know the source impedance. If this is a preceding valve stage, RS (the source impedance) is the grid resistance (Rg) in parallel with the preceding stage's plate load resistor RP in parallel with valve's internal plate resistance rP. Since the latter is variable, it can be determined either by consulting the valve chart, or by direct measurement. Once the total series resistance is known, the -3dB frequency (f3) is ...
f3 = 1 / ( 2π × CMiller × RS ) (Where CMiller is Miller value of the plate-grid capacitance (Cp-g) multiplied by stage gain.
Assume a 12AU7, with a 22k plate resistor, rP of 6,125 ohms, and plate to grid capacitance of 1.5pF. Grid resistance is 100k, and gain (Av) is 10 times. Cp-g is multiplied by the miller effect and becomes 1.5pF × Av = 15pF. RS is 22k || 6,165Ω || 100k = 4,572Ω. The upper frequency limit is therefore ...
f3 = 1 / ( 2π × 15pF × 4,572 ohms ) (Where C is Miller value of the plate-grid capacitance (Cp-g) multiplied by stage gain.
f = 2.3MHz (Note that this is the maximum possible, and fails to consider external stray capacitance)
Performing the same calculation for a 12AX7, we see that the plate to grid capacitance has a much greater effect. We'll assume that the total value of RS is about 70k - typical of a 12AX7 with a 220k plate load resistor. Plate to grid capacitance is 1.7pF, and typical voltage gain is 50. The Miller capacitance is therefore 85pF ...
f3 = 1 / ( 2π × 85pF × 70k ohms ) (Where C is Miller value of the plate-grid capacitance (Cp-g) multiplied by stage gain.
f = 26.7kHz (Again, this is the maximum possible, and external stray capacitance is not included)
To be strictly accurate we should also add the grid to cathode capacitance to the Miller capacitance, but it's usually small and neglecting it does not cause a significant error. Wiring capacitance - especially between grid and plate circuits - may have a surprisingly large effect, especially if the two circuits are close to each other on a printed circuit board. Because normal FR-4 fibreglass PCB material has a dielectric constant of about 4.3, any capacitance that might only be a few pF in air must be multiplied by the dielectric constant, so just 1pF (free air) becomes ~4.3pF because of the PCB material. If this is added to the plate to grid capacitance, HF performance can be seriously degraded. PCB layout for valve circuits is critical, and plate and grid circuits in particular must be kept as far apart as possible.
With all this new found knowledge, it's time to look at a practical preamp circuit that would be usable in a modern system. Input levels might range from about 500mV for a tuner, and about 2V for CD players. Since about 2.5V RMS will drive any power amp to full power, the gain doesn't need to be more than 5 (14dB) - many people who have built the ESP P88 preamp have found that they don't even need that much. As noted above, if RIAA (phono) inputs are needed, use P06 or similar - don't bother trying to use valves as it's not worth the effort.
Figure 1 is the chart for rP, gm and µ for a 12AU7. Since any modern preamp needs only to be able to accept mostly high-level signals, the requirement for lots of gain does not apply. This rules out a high-mu triode such as the 12AX7, and even a medium mu triode like the 12AT7 still has too much gain. The 12AU7 is ideal in all respects, and although the gain will probably still be too high, it's within reasonable limits.
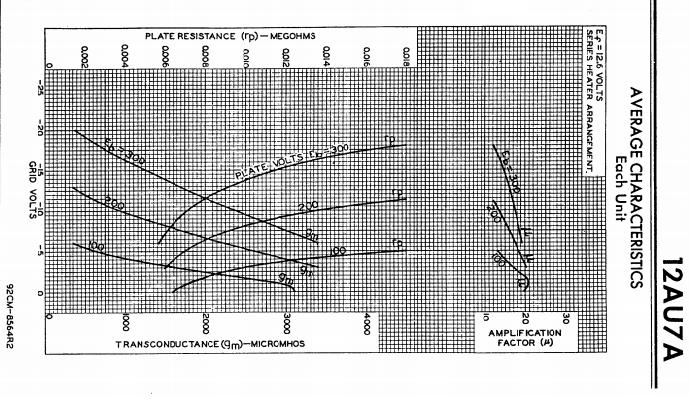
Figure 1 - Curves for a 12AU7
From the bias and gain article, we know that a general purpose triode can be modelled as a voltage source (zero impedance), with the internal plate resistance (rP) in series. Alternatively, it can be modelled as a perfect current source with rP in parallel. Either model works, as they are equivalent in all respects. Personally, I prefer the current source model as it more closely resembles the actual function of the valve.
Figure 2 shows the low frequency equivalent circuit of the stage we are discussing. At high frequencies, inter-electrode capacitance becomes an issue and that will be dealt with separately. This kind of arrangement is extremely common, but in many cases will immediately violate Rule 1, so the valve's load resistance will vary between 1M and 500k at some point that's determined by the voltage where the following valve draws some grid current. At voltages below the onset of grid current, loading is symmetrical, but once the critical voltage is reached distortion is inevitable. Above this critical voltage, the grid current rises exponentially. While it may seem safe to simply keep the peak input signal voltage below the cathode voltage, this is not the case. A valve can draw comparatively significant grid current while the grid is as much as -1V with respect to the cathode, so it's not enough to keep the input signal peaks below the grid bias voltage.

Figure 2 - Valve Equivalent Circuit (Low Frequency)
The critical voltage for grid current varies with different valves, with plate voltage and with age, so a definitive figure is simply not available. However, if you can keep the input signal to such a voltage that ensures that you can maintain at least 1V of negative grid bias even at the highest positive peaks, then this form of distortion is minimised. The reason that grid current flows earlier than expected is based on a number of factors, one being the contact potential developed between dissimilar metals. While the grid and cathode are not in physical contact, they are in electrical contact due to the space charge - the cloud of electrons that surrounds the cathode. The grid and cathode of a valve are typically made from nickel and barium/strontium oxide respectively, and therefore have a small contact potential which serves to change the effective grid voltage. While the contact potential is typically less than 0.5V, it's a moving target. While it can be measured, a very sensitive meter is needed to measure considerably less than 1uA. To be able to get an accurate measurement, you need to be able to measure down to perhaps 100nA, but without introducing significant extra resistance into the circuit. See below for the method I used - it's much easier than trying to take a direct measurement.
Other sources of grid current include ionisation current, caused by gas molecules becoming ionised and returning to the grid to regain the lost electron. Some degree of grid emission is also present, because the grid temperature will be elevated due to its proximity to the hot cathode. While these effects are minor in preamp valves, if allowance is not made for their existence you can easily end up with a circuit that has far greater distortion than the plate curves may indicate. For this reason, any attempt at calculating distortion using the data sheet graphs is utterly pointless and will not be covered here.
The circuit in Figure 2 is biased so that the cathode voltage is 4.1V, allowing for a grid swing of up to 3V peak (2.12V RMS). With a plate voltage of 125V, a 200V supply and grid voltage of -4.1V, gm is about 1.15mA / V. With a 22k plate load resistor, plate current is 3.4mA, and at this current there's 4.1V across the 1.2k cathode resistor. Measured voltage gain is 5.45, or 14.7dB. Based on the chart, rP is about 12k, so µ will be ...
µ = gm × rP / 1000 = 13.8 Because we are using mA / V rather than micromhos, the answer must be divided by 1,000
Since the above circuit was derived by experiment rather than from the charts, it's worth checking to see if the measured and calculated gain are in agreement. Because the cathode resistor is not bypassed, we have to do a couple more calculations than normally, but they aren't difficult ...
Rsource = rP + ( µ × RK )
Rsource = 12k + ( 13.8 × 1.2k ) = 12k + 16.56k = 28.56k
RTot = RP || Rload
RTot = 22k || 100k = 18k
Av = µ / (( Rsource / Rtot ) + 1 )
Av = 13.8 / (( 28.56 / 18 ) + 1) Av = 5.33
Since the measured gain was 5.45, that's fairly good agreement - better than we might normally expect based on charts that aren't particularly clear, and with a recent 12AU7 instead of one from the era when the charts were made in the first place.
Ok, you may ask, what's the purpose of this anyway? It's quite simple - I wanted to have a preamp that would accept an input voltage of up to 2V RMS with less than 1% distortion, and capable of being connected to a 100k pot without using a cathode follower. It also had to have bandwidth to at least 50kHz, and operate from a 200V supply that I have for experiments such as this. I also wanted to be able to test the input voltage that just caused grid current to be drawn, and naturally it had to be less than 2V RMS. Even though low impedance sources are not affected by small amounts of grid current, it's simply a bad idea!
The end result is tabulated below. For any high-level inputs, it would be sensible to attenuate them slightly before the preamp stage as this reduces distortion further.
| Input Voltage | 2V RMS | 1V RMS |
| Output Voltage | 10.9V RMS | 5.45V RMS |
| Distortion (THD) | 0.95% | 0.42% |
| -3dB Bandwidth (10kΩ Source) | 85kHz | 85kHz |
I did manage to work out a way to determine when grid current started. The source impedance was changed from 10k to 220k, with the input voltage adjusted as needed to maintain exactly the same output voltage. Distortion was measured for both source impedances. If there is no grid current, distortion will be the same regardless of source impedance (for the same output voltage). The input voltage was increased in stages until a difference of 0.01% THD was detected, with the higher distortion appearing with the high source impedance. The higher distortion reading can only be caused by grid current, and although it was only a few nanoamps for the distortion change I looked for, it rises very rapidly beyond the level where distortion starts to increase.
I found that with this particular valve, and under the operating conditions shown above, that grid current was detectable with an input voltage of 2.18V RMS (3.1V peak) - exactly 1V below the voltage where one expects grid current. This is in substantial agreement with the details shown above, and at higher input voltages it was easy to measure the distortion of the input signal itself (using the high impedance source resistor).
As you can see, there is an almost endless stream of compromises, and the designer's job is to rationalise these down to a final circuit that does what's needed. In this case, we need to decide if we really need a gain of 5.45 - in most cases, the answer is no. The gain needs to be reduced further, and the easiest way to achieve this is to use additional feedback. With a single stage amplifier, that means that the input impedance will be reduced, and this might cause other problems.
To be really useful, a preamp should have less than 0.1% distortion, primarily to ensure that intermodulation is negligible. While the proponents of 'no feedback' don't seem to hear the effects of intermodulation distortion, it is by far the most objectionable form of distortion known, and is the inevitable result of harmonic distortion. As I found with an earlier experiment, less than 5% (of predominantly second harmonic) distortion creates intermodulation products that render the sound unlistenable - and that's through my workshop system. In a hi-fi setting, the effect will be much, much worse.
Of all the forms of distortion, intermodulation distortion (IMD) is by far the most grating. The effect is listener fatigue, and complex music in particular just becomes a mess of sound. Differentiating between instruments becomes difficult, and a great deal of potential enjoyment is destroyed. There is no simple way to determine IMD from a simple THD (total harmonic distortion) measurement. Reference 1 provides a very simplified formula, but it only applies if the THD is low, and relies on the two forms of distortion that cannot exist in isolation (this is stated).
For an amplifier that produces only second harmonic distortion (2HD), IMD is approximately 3.2 times the THD. For a circuit that produces only third harmonic distortion (3HD), IMD is 3.8 times the THD. All real circuits produce at least two harmonics, and some produce many more. 2HD and 3HD are both produced in a triode amplifier that is operating in its most linear range, but at the lowest levels 3HD is minimal, to the point where the distortion residual looks just like a sinewave on an oscilloscope. Needless to say, further examination reveals that 3HD is indeed present, as are fourth, fifth and so on. Especially with valve stages, it's very common that the harmonics above the third may be buried in noise, and are therefore effectively inaudible. While it is often possible to hear a tone that is well below the noise level, this does not apply when there are also other harmonically related tones present at the same time and at much higher levels. This effect is known as masking, and is the basis for lossy audio compression algorithms such as MP3.
There are many ways to measure IMD, but few of those used in the valve era are sensitive enough to reveal the detail that's available to us now. Consequently, I will not bother describing any of the old methods. While they were appropriate in the 1950s, the methods used at the time are now well past their use-by date. The tool of choice now is FFT - Fast Fourier Transform, a technique that is even available on freeware PC programs that allow the sound card to be used as an oscilloscope. While the sound card based systems have limited bandwidth, it's still sufficient for reasonably accurate measurements if the frequencies are chosen to be well within the card's capabilities.
For those who may not know exactly what IMD is, it's worthwhile to provide a brief explanation. If two signals are mixed together with a perfectly linear system, then the output is simply a mixture of the two frequencies. For this example, we'll consider 400Hz and 500Hz at equal levels. Mixed with resistors, the output will consist of the two frequencies and nothing more. If this signal is now applied to a simple non-linear amplifier, we will get the original two frequencies, their second harmonics (800Hz and 1kHz) and perhaps some third harmonic (1.2kHz and 1.5kHz). The test circuit was the open loop FET SRPP circuit shown below (Figure 3), with open loop distortion of 2.7% at a peak output level of 11V.
So, in addition to the harmonic distortion, we also get the sum of the two frequencies (900Hz) and the difference (100Hz). So the two frequencies have become a sequence (figures in bold are the two we started with, those in italics are at levels greater than 100mV or -34dB) ...
100, 200, 300, 400, 500, 600, 700, 800, 900, 1k, 1,1k, 1.2k, 1.3k, 1,5k, 1.7k. 1.8k, 1.9k, 2.0k, 2.1k, 2.2k, 2.3k, etc.
As if that's not bad enough, we may also get the sum and difference frequencies of the distortion products, and if the signal is amplified again by a non-linear amp, the whole process starts again with all the new frequencies as normal input, so the number of output frequencies just gets worse. IMD is by far the most objectionable kind of distortion, and is unavoidable in any circuit that has even the allegedly 'benign' predominantly second harmonic distortion. No distortion is benign, simply because its presence indicates that non-benign distortion comes free, whether you like it or not.
Note that all of the above frequencies up to 1.9kHz are greater than 1mV, which is above the level of -74dB referred to the input voltages (5.3V RMS for each frequency). There are lots more harmonics, but they are below the -74dB cutoff level I chose. Those above 1.9kHz are shown for reference only. As you can see, the sum and difference signals are well above the harmonic distortion levels.
Another form of IMD is AM (amplitude modulation). While this is very common with valve guitar amps, it should never be present in anything that claims to be of even fairly low-grade fidelity. I mention it because it was (apparently) common with low-end valve equipment in the '40s and '50s. If there is any evidence of amplitude modulation, all other forms of distortion can be considered severe, and such a system is simply not worth listening to.
AM is easily explained in a valve circuit. If one measures the gain at low level (say 1V RMS output) and finds it to be 50, but when measured at a higher level (eg. 15V RMS), it may be less - depending on the configuration gain might fall to perhaps 40 or less. If these output voltages are within the normal signal range for typical music reproduction (the source is immaterial), then a loud bass passage for example will reduce the gain of quieter background sounds - the result is extremely unpleasant, especially since the total of all other distortions have already made the signal quality intolerable.
During the valve era, the 20Hz to 20kHz we now consider to be the minimum acceptable was considered very wide range. Many lower grade systems were deliberately band-limited to reduce the audibility of distortion. Mantel radios generally had a frequency response from around 150Hz to 5kHz (some were even worse), because a reduction of bandwidth was the only way to make the sound quality acceptable. It was discovered quite early that by limiting the bandwidth, an otherwise intolerable amount of distortion could be made acceptable to the average (casual) listener. By limiting the bass and treble response, there is less chance of AM distortion, and many of the upper harmonics are filtered out - either electrically or by the loudspeaker itself.
Consider that a perfect squarewave at 1kHz will sound and measure just like a sinewave if filtered (with a 'brick wall' filter) at 2.8kHz. This shows that by limiting the high frequency response, harmonic content can be reduced dramatically. IMD is another matter however - all IMD products that fall below the cutoff frequency are still present. It is generally accepted that the high harmonics (from the seventh and beyond) are discordant and/or objectionable, so the simple trick of including a 'tone control' that only acted to reduce the high frequencies was popular with a great deal of valve based consumer products. Most people would reduce the treble because that also reduced the audibility of the upper harmonics, so the equipment generally sounded better when used like that. For some of the older generation used to old valve equipment, the presence of properly balanced and extended high frequency response is disconcerting in the extreme, until they get used to the 'new' sound.
By far the easiest way to improve performance is to add transistors or FETs as current sources, but this is about a valve preamp, so it's not the approach I'll take here. Distortion minimisation is not an area that I've really looked at, since most of my valve experience was with guitar amps, where distortion is a desired outcome. As a result, experimentation is needed to determine the best way to get very low levels of distortion with the very moderate gain that's needed for hi-fi.
One approach that has considerable presence on the Net is the SRPP circuit, as shown below in Figure 3. This is a version that I built to test, since any attempt to work the design mathematically using valve characteristic charts is simply too cumbersome. Having looked at quite a few preamps from a variety of manufacturers of the valve era, many of them have insanely high gain, which is reduced to something sensible by attenuators or feedback. In most cases, it's better to keep feedback fairly low with low gain devices such as valves. This is one of the few circuit arrangements where adding feedback can increase the level of high-order harmonics, even though overall distortion is reduced.
The circuits shown below are both SRPP - one using FETs and the other valves. The FET circuit was simulated, but I had to build the valve circuit as my simulator doesn't understand valves. There is an option on both to disconnect the feedback so open-loop distortion can be measured, and naturally without feedback the gain is higher. All measurements (simulated and actual) were performed at about the same output voltage ... approximately 10V peak or 7V RMS. Although this is higher than we would normally ever need, it means that at any lower level distortion will be reduced roughly in proportion to the level difference. For example, the FET circuit gives 2.7% THD at 8V RMS, falling to 0.28% at 800mV output. Both circuits were loaded with a 22k resistor to provide an impedance typical of that of a power amplifier.
Please note - the JFETs shown are rated at a maximum voltage of 25V, and were only used in a simulation. Do not build the circuit as shown, because the FETs are liable to be damaged due to excess voltage. To use the circuit, the supply voltage should be reduced to no more than 30V, preferably 25V. Resistor values may need to be changed to obtain results similar to those I simulated.
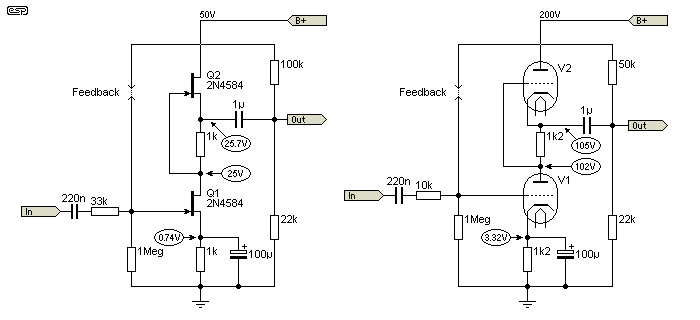
Figure 3 - FET And Valve SRPP Circuits
Because it's easy to simulate, I tried a pair of FETs in the SRPP configuration. Open loop gain measured 112 (41dB) which is obviously much too high, but I wanted to measure distortion and IMD with open loop and with feedback. At 8V RMS output, THD was 2.7% - already above a sensible level. After feedback, the THD was down to 0.13% - a little high, but the output level is well above normal. Gain was somewhat arbitrarily set for 3 (9.5dB), although from experience it is more likely that a gain of 2 (6dB) is sufficient. Two such stages, one before and one after the volume control, typically give more than enough range for 99% of systems. Frequencies shown in bold in the table below are the original frequencies - all others are distortion artefacts.
| No Feedback - THD: 400 Hz tone, 100 mV input, IMD: 400 Hz + 500 Hz, 50 mV Each | ||||||||||
| Freq. | 100 | 400 | 500 | 800 | 900 | 1k | 1.2k | 1.5k | 1.6kHz | 1.8k |
| THD | - | 10.6 V | - | 288 mV | - | - | 39 mV | - | 4.4 mV | |
| IMD | 148 mV | 5.3 V | 5.3 V | 73 mV | 145 mV | 71 mV | 5 mV | 5 mV | 270 µV | 1.6 mV |
| With Feedback - THD: 400 Hz tone, 4 V input, IMD: 400 Hz + 500 Hz, 2 V Each | ||||||||||
| Freq. | 100 | 400 | 500 | 800 | 900 | 1k | 1.2k | 1.5k | 1.6kHz | 1.8k |
| THD | - | 10.4 V | - | 13.7 mV | - | - | 3.1 mV | - | 171 µV | - |
| IMD | 7 mV | 5.2 V | 5.2 V | 3.6 mV | 7.3 mV | 3.6 mV | 420 µV | 420 µV | 15 µV | 71 µV |
| Reduction | 26.5 dB | n/a | n/a | 26 dB | 32 dB | 25.9 dB | 21 dB | 21 dB | 25 dB | 27 dB |
Note that there are several frequencies missing from the above, even though they exceeded other levels in some cases. This is simply because there are so many, I just used the most obvious frequencies and those that also coincided with simple harmonics. The full sequence of frequencies up to 2kHz is shown above. Note that with feedback applied, every harmonic and intermodulation product is reduced - most dramatically. The row 'Reduction' is the reduction (in dB) of each distortion frequency between feedback and no feedback. The two fundamental frequencies are indicated as not applicable, because the reference level for them is the same as the previous test.
It is possible to manipulate the figures to make it appear that the distortion levels are actually higher with feedback than without, but this is charlatanism at it's very best. Distortion (including intermodulation) is reduced across the board, and it is wrong and silly to imagine it to be otherwise. Any test equipment or simulation will show very clearly that negative feedback reduces distortion. If it were otherwise, I feel reasonably certain that someone would have noticed by now.
The valve stage was not measured for IMD, only THD. This is because setting up an IMD test is somewhat irksome, and I know that if THD is reduced, so too is IMD - and usually by roughly the same amount (as shown in the table above). I also tried the SRPP circuit with no cathode bypass cap. Although there is an improvement, it's small, and is roughly in proportion to the gain reduction.
| 12AU7 - Open Loop SRPP | ||||
| Vin | Vout | Av | dB | THD |
| 1.0 V | 10.2 V | 10.2 | 20 | 1.5% |
| 196 mV | 2.0 V | 10.2 | 20 | 0.3% |
| 12AU7 - Feedback SRPP | ||||
| Vin | Vout | Av | dB | THD |
| 3.35 V | 10.0 V | 2.98 | 9.5 | 0.74% |
| 671 mV | 2.0 V | 2.98 | 9.5 | 0.14% |
| 12AU7 - Feedback SRPP, No Cathode Bypass | ||||
| Vin | Vout | Av | dB | THD |
| 4.54 V | 10.0 V | 2.2 | 6.8 | 0.46% |
| 909 mV | 2.0 V | 2.2 | 6.8 | 0.11% |
I also tried a 12AX7 in the same circuit, but it was not a resounding success. Distortion at 2V output was 0.11%, and at 10V was tolerable (0.9%), but contained significant second and third harmonics. This would no doubt be a lot better if the cathode resistors were optimised, but open loop bandwidth was much worse than the 12AU7 versions, because of the much higher gain. Another circuit was also tried - a simple plate loaded amplifier with a cathode follower output. With a 12AU7, this circuit had 0.18% THD at 10V and a rather better figure of 0.014% at 2V - this makes it the clear winner. With a fairly sensible gain of 2.4 (7.6dB) it also had the widest bandwidth, being only 0.2dB down at 285kHz (the maximum from my oscillator).

Figure 4 - 12AU7 Feedback Amplifier Circuit
This is part of the circuit I used in the valve preamp I used some time ago (in fact, all valve preamp tests were done using the board and power supplies I built for it). Despite the rather common-or-garden circuitry, it is a fairly clear winner. While the SRPP circuit is more interesting, and with a higher supply voltage and rigorous optimisation may be slightly better, the performance of this circuit is not too bad at all. Again, optimisation may improve performance, but it's still a far cry from the performance and ease of use of opamps.
While it has a significantly higher headroom than any opamp circuit, there is no common music source that can deliver more than about 2V RMS anyway, so it's an academic consideration that has no relevance to reality. I freely admit that I almost certainly deluded myself when I was using this preamp, and doubt that I could pick the difference (in a blind A-B test) between the valve circuit above, an IC opamp, or a discrete transistor opamp such as the P37 circuit at any normal listening level. All have distortion that is generally below the limits of audibility, and bandwidth that is far greater than that of the source material. The cue to picking the valve preamp might be noise level, as it's a little higher than most solid-state stages with similar gain.
This next circuit is one that I originally designed for an amplifier which was designed and built by John Burnett and me for AMW ... just before they ceased operations. It's not original (although I thought so for some time), and I've subsequently seen that this arrangement was published in Wireless World magazine in 1947 (but that used a pentode). The circuit is remarkably similar to a transistor preamp I designed many, many years ago (see Project 13). Even the plate load resistors are (coincidentally) the same value.
This really is as good as it gets, with distortion that is far lower than any of the arrangements described above. The only optimisation was to select the optimum cathode bias resistor, and as shown it was operated from the same 200V supply I used for the other tests. This preamp has a low output impedance, and with no feedback can still give 10V RMS at less than 0.1% THD.

Figure 5 - Bootstrapped Load Feedback Amplifier
The plate load resistor to the amplifier valve (V1) is split into a pair of 39k resistors. The midpoint is driven via a capacitor from the output of the cathode follower, which results in the voltage across the lower 39k resistor remaining substantially constant. If the voltage is constant, then so is the current, and this linearises the amplifier valve's output, giving the lowest possible distortion. Although I've not attempted a full optimisation, the overall performance is already so much better than any of the traditional circuits that I didn't bother. I have absolutely no doubt that it can be made better still, but as explained in the conclusion, there really isn't much point.
With feedback applied as shown, voltage gain is 4 (12dB), and distortion at 10V output is 0.03% (no, that's not a misprint - 0.03%) - and that's driving a 50k load. At 2V RMS output, I can't even measure the distortion, because it's the same as my signal generator (0.014%). At higher voltages, the distortion is predominantly third harmonic, which appears to be a direct result of the bootstrap circuit. The level is so low that it's below the limits of audibility until the output voltage is well above anything even remotely sensible. With a measured output impedance below 1k (without feedback), this circuit probably is as good as they come. The low output impedance means it can drive long interconnects with no loss of treble response. The weak point is actually the cathode follower, since its limited current and gain reduces the performance slightly.
Optimisation would include selecting a more linear valve (a 6DJ8 for example), and changing the supply voltage, plate and cathode load resistors for the values that give the lowest possible distortion and the highest output voltage. As it is shown here, it already beats any of the other topologies hands down (I used the same 12AU7 for all tests). We are close to the levels of distortion found in an opamp circuit, and since high quality opamps are far cheaper than valves it seems silly to continue.
Most people will think of operational amplifiers (opamps or op-amps) as being fairly recent, but they were used in the late 1930s through to the early 1960s, built using valves. Many of the earliest popular valve opamps were made by Philbrick (George A. Philbrick Researches, or GAP/R), and many of our most common applications came from these early disciplines. The valve opamp was rather constrained compared to its modern equivalent, and was generally only operated in inverting mode.
The non-inverting input was commonly reserved for an 'offset null', allowing the operator to set the output to zero when no input signal was present. The following is the schematic of the Philbrick K2-W, the first truly modular plug-in opamp. Another reasonably representative example of the era is shown in a 1962 copy of the American magazine 'Electronics World' (not to be confused with the UK magazine 'Wireless World' which changed its name to Electronics World many years later).
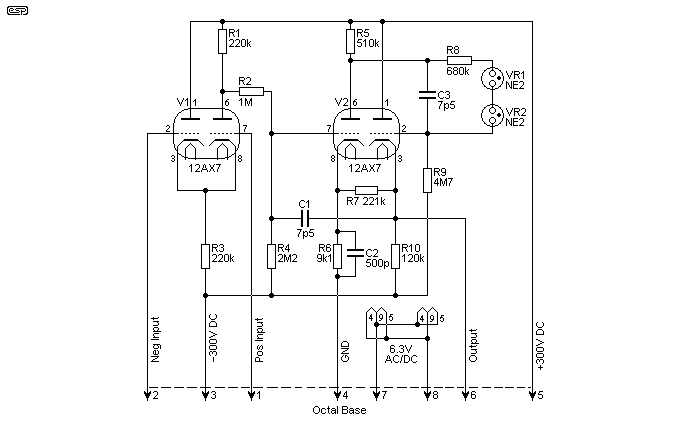
Figure 6 - Philbrick GAP/R K2-W Operational Amplifier Circuit
There were many systems using valves that performed similar functions to the 'opamp', but the term wasn't coined until some time in around 1946-7, by John R. Ragazzini. There is some speculation that the original design of these modular circuits was done by a young engineer working at Columbia University, Loebe Julie, although Ragazzini apparently took the credit. The famous Robert A Pease (aka Bob Pease, RAP) was involved in much of the early design work, and Philbrick was the first to commercialise the opamp as a plug-in module. The K2-W was one of the first, and despite its not inconsiderable cost was very popular through the 1950s and 60s until the introduction of the first fully integrated version - the venerable µA702. Philbrick also made 'solid state' opamps once transistors were readily available, but they were in potted modules rather than ICs (which came along much later).
Alan Blumlein patented the circuit we now call a 'long tailed pair' in 1936, with the cathodes of two triodes tied together and using a common cathode resistor. This was the birth of the differential amplifier which is the heart and soul of any opamp. One of the earliest IC opamps was the µA702 in 1964 (by Fairchild), and the rest (as they say) is history.
For those interested (and it is a very interesting topic) I suggest a search for 'opamp history' or something similar. This is the birth of the 'new' era of electronics, and it's worth knowing about.
The design process for a high fidelity preamp involves many issues that must be overcome. So much so that it is difficult to recommend valves for this application. There are many other valve types that I don't have to hand, but a review of various commercial and DIY offerings shows that for the most part, distortion is generally not as low as it should be. This is compounded by the fact that transistorised power amps generally have low impedance inputs as far as valves are concerned. The simple fact of the matter is that valve stages just don't like feeding low impedances unless a matching transformer is used. While cathode followers and feedback help, the load should draw considerably less than one quarter of the total valve current at the highest level encountered.
Even when a valve stage has a low value (22k) plate load resistor, even 100k of external loading will change the optimum bias point and/or the distortion. Application of feedback can maintain a reasonable stage gain, but loading will almost always create problems. Any applied load changes the current through the valve itself, since some current (however small) is required by the load. Valve stages are sensitive to the plate current, and even a small change can cause an easily measurable change of output level and distortion. Compare this with transistor or opamp designs, where loading can usually be anything from infinity to less than 10k, with absolutely no audible (or measurable) change in gain or distortion. Note that harmonic distortion is considered only by virtue of the fact that any non-linearity causes intermodulation distortion. While simple (low order) harmonic distortion may not be objectionable if it could be had in isolation, the intermodulation distortion (IMD) that results from any non-linearity is extremely unpleasant. Since one is not available without the other, it follows that distortion must be low to avoid intermodulation. IMD can also occur in amplifiers that are (or appear to be) reasonably linear and is the ultimate test of any preamp or power amp. Poor IMD performance means bad sound quality, regardless of the technology used for the amplifier.
All valves change their characteristics over time, so while the selected bias current might be optimum when the valves have had perhaps 100 hours of use, after 1,000 hours or more it is probable that distortion (in particular) may be very different. Needless to say, it's highly unlikely that anything will get better, so we can expect performance to degrade as the valves age. Added to this is the fact that all valves are microphonic to some extent. Tapping a preamp valve will almost always elicit an audible response through the speaker, so any signal from the speaker may excite the internals of the valve causing colouration. With proper mounting techniques and damping this can be minimised, but it never goes away. Normally, one should look at expensive isolated equipment bases as being totally unnecessary, but with a valve system a suitable isolated base is usually a good idea.
Although it's very easy to make a valve preamp stage that works (and might even sound alright), it's another matter entirely to get it right. This means that distortion should be very low, noise and microphony must be minimised, and performance should remain fairly consistent over the life of the valves. The only way that this can be achieved is to apply feedback - as much of it as possible. Once the distortion is below 0.1% and remains there for the life of a set of valves, it's highly unlikely that anyone would be able to pick a valve preamp from an opamp version in a blind test - provided noise levels and frequency response are comparable of course.
Once no-one can pick the difference between equivalent valve or solid state equipment in a blind A-B listening test, then there's obviously no point using the valve equipment because it is far more costly, requires periodic valve replacement and generates a great deal more heat - all for no audible difference. This tends to make the whole idea rather pointless, unless you like distortion and choose a preamp that adds 'colour' to the sound. The problem with this approach is that you don't have a knob or switch that allows you to select between 'coloured' and 'uncoloured' so you can choose the setting that suits the music or your mood.
Given the difficulties of making a valve preamp that will retain its performance for many years without attention, I can no longer see any point to using valves for hi-fi preamps - despite the time taken to evaluate the circuitry described in this article. At one stage (a few years ago) I was using one, and while I really liked it at the time, I have been using a completely solid state system for at least 8 years at the time of writing. I can't even begin to imagine the difficulties (or the cost, including running & maintenance costs) involved in making a valve preamp with RIAA equalisation, 3-way, 24dB/octave active crossovers and adequate line drivers for the six power amps plus subwoofer that make up my main system.
There can be no doubt whatsoever that most of the systems of the 1940s and 1950s were exceptionally poor performers by today's standards - obviously some were suitable, but very expensive. Earlier systems were even worse, because neither microphone or loudspeaker technology could (re)produce a wide range, low distortion signal. As a result, there was no point trying to build amplifiers whose benefits could not be heard using existing microphones, radio (wireless) broadcasts or loudspeakers. Only when high quality material and speakers became available was there any point to making an amplifier that had respectable performance. All improvements involved greater complexity and higher cost at that time, and almost no-one would pay extra for equipment that sounded no better than anything else.
Home audio (aka hi-fi) owes a lot to professional audio, from cinema systems to studio monitors, but prior to the Acoustic Research AR-1 in 1954 and the first Quad ESL (electrostatic loudspeaker) in 1957, few home loudspeakers could really be considered hi-fi. By today's standards, neither of these examples is outstanding, nor were any of the other systems available at the time. Some theatre systems had reasonable fidelity, but most were highly coloured - leading to the classic 'theatre sound' that was still fairly common in the 1970s. High quality material was rare until (perhaps, at a stretch) the mid 1950s, and the BBC in the UK and a few others elsewhere provided the highest quality material available with direct FM broadcasts from concert halls.
Prior to 1940, shellac (78 RPM) recordings were generally limited to about 6kHz, and even in 1957, most vinyl discs were only capable of 8 - 10kHz, with a few extending to 15kHz. Vinyl discs capable of 20kHz didn't arrive until some time in the 1960s. To imagine that circuitry that was suitable for shellac recordings in 1940 is somehow not only suitable but better than modern circuitry for playback of CD or SACD quality recordings is clearly preposterous.
 Main Index
Main Index
 Valves Index
Valves Index