

|
| Elliott Sound Products | Valves (Vacuum Tubes) - Biasing and Gain |
 Main Index Main Index
 Valves Index Valves Index
|
Having decided that you want to use valves in your preamp project, it is necessary to understand the transfer curves and know how to bias the valve to get the desired result. Most applications also require a specific gain, but we need to know how to work that out or we're stuck with the 'hit or miss' technique. Not that there's anything wrong with using a test setup to determine the optimum values, but unless you go through the calculations you don't learn anything.
Unlike opamps, valves have a relatively high output impedance. This means that the gain is determined not only by the stage itself, but by any circuitry that follows the stage. As a result, gain is often much lower than expected because this has not been considered. There are also a few tricks that one needs to understand if noise is to be kept to a minimum. All active electronic devices make noise, but valves introduce a noise source not experienced by transistors or opamps. This will be looked at later in this article.
One of the claims you might come across is that valves are inherently linear, while transistors are not. This is false! Valves are actually quite non-linear, and some are much worse than others. I expect that this myth came about in the early days of transistors, and there's a simple explanation. Audio signals haven't changed much in amplitude since the beginning, so the AC signal voltages after amplification are generally within the range of 1-5V RMS. There will be exceptions as always, but in general this is a fair guess.
A valve stage with a supply voltage of perhaps 250V and an output of 5V means that the signal level is only one fiftieth (1/50) of the supply voltage. With such a small relative change, the overall linearity will be quite good. In contrast, early transistor equipment used a supply voltage of around 20V, and 5V is one quarter (1/4) of the supply voltage. The transistor circuit therefore had to swing much closer to the supply and earth (ground) than an equivalent valve circuit, so non-linearity became more of an issue. Despite this, many of the traditional transistor circuits can have distortion that is comparable to that of an equivalent valve design (and in some cases considerably better, especially with feedback amplifiers).
Speaking of feedback, this has been blamed for everything - 'bad sound', 'smeared' stereo imaging, transient distortion and ingrown toenails (ok, maybe not the latter ... yet). Feedback was invented in the valve era by Harold Black, U.S. Patent 2,102,671 filed in 1932, issued in 1937. It was used extensively in telecommunications equipment to reduce the distortion that plagued early systems. Almost all valve amplifiers gain benefit from the use of feedback, with greatly reduced intermodulation distortion in particular. This is not a bad thing.
Note: In numerous places in this article, you will see the symbol || This simply means 'in parallel with'.
Something that is rarely mentioned other than in passing is the maximum input level that a valve can handle. If you don't mind having lots of distortion as well as other equally undesirable side-effects then just connect a valve input stage to any old signal level and hope for the best. If you'd prefer to get the best linearity from a valve stage then you need to understand the input voltage limits.
When a valve is biased, there is a defined voltage between the grid and cathode that sets the operating conditions. This is described in more detail below. We'll assume that the cathode bias resistor is bypassed with a capacitor, because that's almost always necessary to get the maximum gain and lowest noise. The absolute maximum input level is then determined by the voltage across the cathode resistor. As an example, the cathode may run at +1V DC - see below for the design decisions that have to be made.
The input voltage to the grid must never exceed 1V at the positive peaks, or the control grid will become positive with respect to the cathode and it will act like a diode (which it is). This means that the absolute maximum input voltage is 707mV RMS (sinewave), but preferably no more than 500mV. If your input voltage is greater than that, the valve will distort because grid current will be drawn during positive peaks. For high input levels, it is essential that the signal is attenuated before it reaches the grid to ensure that there is no chance of grid current. This is one of the main reasons that vintage valve preamps have a much higher sensitivity (lower input levels) than a modern opamp based equivalent.
If you are using a valve preamp with a CD, SACD or DVD player, the output level is far too high for most input stages, and has to be reduced to prevent gross distortion. Obviously, this limitation doesn't apply if the unit's volume control is placed before the first amplifier, or if there is an option to bypass the input valve with the normal input switching.
Higher input levels can also be used where the valve is part of an overall feedback network, or uses an unbypassed cathode resistor. The latter approach may not provide very much improvement though, and would need to be tested thoroughly in the final circuit to determine the maximum input level. Because the possibilities are almost endless, you can only find out the highest permissible input level from the operating manual for commercial equipment, and/ or by measurement.
Before we begin, it's useful to look at the equivalent circuit of a valve. In some texts, you see it shown as a voltage source (VCVS - voltage controlled voltage source) with a series resistance. While this is correct, it is less intuitive than the real equivalent - a voltage-controlled current source (VCCS). Functionally, the two are (almost) identical, but the VCCS is more in line with the real way a valve works. As described below, the VCCS model doesn't work for some configurations, and the VCVS doesn't work for others. Interestingly, only one reference I've seen so far uses the VCCS model, and that is applied to pentodes because the VCVS model doesn't work. All very confusing - and somewhat less intuitive than semiconductor design (but that's another story altogether  ). The two models are shown below, along with a triode amplifier for reference ...
). The two models are shown below, along with a triode amplifier for reference ...
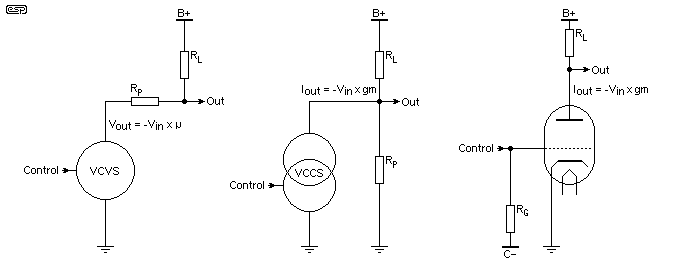
The most basic triode based valve voltage amplifier is shown above. Referring to the positive supply as 'B+' is historical. In the early days, the 'A' battery supplied the filaments, the 'B' battery supplied the high tension (usually about 90V), and the 'C' battery was used to bias the valves. Of these, B+ has remained, and almost everyone who worked with valve equipment will continue to use the term. A and C batteries fell from favour long ago, but most of the older generation of electronics people will know the terms.
Note that all output voltages are indicated as negative. A single valve amplifying stage inverts the signal, so as the input swings positive, the output swings negative with respect to the quiescent voltage. Single stage transistor or FET voltage amplifiers do the same, since in all cases a more positive input signal causes more current to flow in the amplifying device, so its output voltage must fall.
Those who read the valve primer will recall that in the early days of valves, resistors (as we know them today) were not available. Even up until around 1950, resistors were generally available in 10% and 20% tolerance only (so a 100k resistor could be anything from 80k to 120k - hardly a precision component). While close tolerance resistors existed, they were expensive, and completely unsuited where high stability was also needed. Close tolerance stable resistors were almost always wirewound which brought problems too, as they had considerable inductance in the higher values. By using the C battery, valves could be biased via a resistor, but accuracy wasn't a consideration - anything from 100k (or less) to several Megohms would work fine because (in theory at least) there is no current in the grid circuit to cause a voltage drop across the resistor. In reality there is always some current, but it is generally small enough to be ignored unless the valve is faulty.
While the configuration using a negative grid supply certainly works, it is inconvenient because a separate low voltage negative supply is needed. Nonetheless, the three circuits above are functionally equivalent.
With semiconductor designs (transistors or opamps), the first thing we determine is the gain needed, because it is very easy to get the exact gain you need from these circuits. Valves are another matter - to some extent, the gain is decided by the valve itself, and attempting to obtain a specific gain may result in unexpectedly poor performance in other areas. The first thing we must do with valves is to decide on the operational parameters, and the gain we get is what we get. There are certainly a number of approaches we can take that will reduce the gain if necessary, but they come later.
One figure that can be used for this is the 'amplification factor', µ. Although it's a theoretical figure we can use it, but doing so can be somewhat tedious. Indeed, getting exactly the gain you need from valve stages is always more tedious than using opamps, because the gain of an opamp is set only by resistors. With valves there is a more complex relationship that includes the plate resistance, amplification factor, external load resistor, power supply voltage and the input impedance presented by the next stage.
Before we worry to much about gain, the first step is to bias the stage. This part is pretty easy - the hard part is determining the optimum plate current for the available voltage - we'll look at that more closely a little later. For the time being, we can simply assume a few (perfectly reasonable) values to test the theory. Let's use a 100k plate load resistor, and a nice simple 1M as the next stage. All of these appear in parallel as far as the internals of the valve are concerned, so we must know the plate resistance of the valve. A 12AX7 has the following (basic) parameters ...
| Plate Volts | Plate Current | Grid Volts | Mutual Conductance | Amplification Factor | Plate Resistance |
| 250 | 1.2 mA | -2 V | 1,600 µmhos | 100 | 62.5 k |
| 100 | 0.5 mA | -1 V | 1,250 µmhos | 100 | 80 k |
The above is from Miniwatt Technical Data - basically a short-form listing with working examples, but enough for this first example. If the stage is designed as a first amplifier that may have an maximum input of (say) 100mV, the 100V supply is preferred, as this means it can have extra filtering for lower noise. If we have a 150V DC supply available for the stage, that means we need to drop 50V across the plate load resistor, at a current of 0.5mA. Ohm's law indicates that the plate resistor must be 100k (R = V / I = 50 / 0.5mA = 100k). Since this is in parallel with rP and RG of the next stage, the total load resistance is 42.5k.
At a plate voltage of 100V, the mutual conductance is 1.25mA/ Volt (remember - 1,250µmhos = 1.25mmohs = 1.25mS¹ = 1.25mA/ Volt). If the input is varied by 100mV (RMS or peak as you prefer), the valve current will vary by 1.25 × 0.1 = 0.125mA. This current across the total load resistance (42.5k) causes a voltage change of 5.3V - the gain is therefore 53. With this configuration the gain can't be increased substantially, but it can be reduced simply by reducing the value of the grid resistor of the following stage (or simply adding additional loading), or adding a bias resistor in the cathode circuit, as described next. This is one of the disadvantages of valve stages - often to make useful gain changes a different valve has to be used, which commonly means a change of all resistance values as well.
¹ The SI unit for mutual conductance is the Siemens. 1S is equal to 1moh, 1,000mmoh or 10,000µmoh. Most 'valve people' will still use mohs or mA/V rather than Siemens.
As noted above, the valve must be biased so that it operates within the range you select. It's not difficult, and in many cases a rough (educated) guess will get you pretty close to what you need. Care is needed though. Valves are all rated for a maximum cathode current, and this should not be exceeded. Doing so can cause cathode 'stripping' where the emission enhancing materials on the cathode's surface are forcibly removed by the flow of electrons. For the 12AX7, the limit is 10mA, but it would not be sensible to operate the valve at much above 3mA. Typical currents are in the range of 0.5-2mA, although operation down to a few microamps is perfectly ok for some applications.
All valves have a maximum plate dissipation too, and again, exceed this at your peril. For the 12AX7, the maximum is 1W. Plate dissipation is simply the product of plate voltage and current - 100V at 1mA is 100mW. Note that power dissipation in all valves is average, and not peak as is the case with semiconductor power ratings.
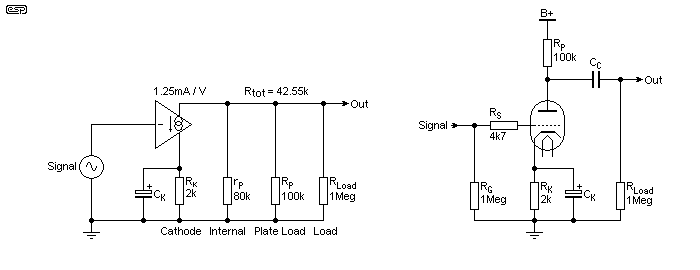
Based on the same info we used above, a circuit can be drawn for a biased valve stage and the equivalent circuit using a VCCS. The addition of a resistor in the cathode circuit has two effects. Firstly, we want a plate current of 0.5mA, and from the table, we know that requires a grid voltage of -1V. By placing a selected resistor (R = V / I = 1 / 0.5mA = 2k) in the cathode circuit, when a current of 0.5mA flows through the valve, 1V will be developed across RK. If the grid is connected to earth (ground) via a resistor, the cathode voltage is 1V greater than the grid voltage, therefore the grid is at -1V with respect to the cathode. All requirements for bias are satisfied.
However, by adding this resistor, some of the input voltage will also appear across it, and this reduces the gain. The amount of signal voltage that appears across RK is not so easily worked out, because it is subtracted from the input voltage as far as the valve is concerned - this is local feedback (actually degeneration), and the effects are interdependent. To get an accurate gain figure, the formula is reiterative, and it's no real surprise that few sites attempt to provide the maths needed to get (even close to) the right answer. Unlike a transistor stage where the effective device gain is extremely high, valves have limited gain and simple formulae can't be used. For the time being, we'll simply bypass the resistor with a capacitor. The capacitive reactance must remain small compared to the value of the resistor at the lowest frequency of interest, and full gain is restored. This will be covered in more detail at a later stage.
The valve is now biased, and using cathode bias is the optimum for all low-level stages. It's self-correcting to some degree, so as the valve ages the bias conditions won't change by much - this is because using a cathode resistor provides a measure of DC negative feedback, so the bias is stabilised against most disturbances - not completely, but enough to prevent any major change in operation.
The small resistance (RS) in series with the control grid is commonly referred to as a 'stopper' - it is designed to prevent the valve from detecting (mainly) AM radio transmissions, and generally does a fairly good job. The assumption is that the source impedance for stray RF will be fairly low (a few hundred ohms at most), so the relatively low resistance of the stopper will be significant. It has no effect on the wanted signal level appearing at the grid, but if made too large (22k or more perhaps), can lead to premature high frequency rolloff in the valve itself, due to the plate to grid capacitance.
Grid stoppers are also used where parasitic oscillation is a problem, and effectively introduce a simple filter into the circuit. Typical values range from as low as 1k to perhaps 22k in extreme cases (uncommon though). The input valve is the most susceptible to stray radio interference because of its connection to the outside world. Stoppers must be placed as close as possible to the grid pin to be effective, preferably wired directly to the valve socket with the minimum of excess resistor lead.
The peak input voltage at the grid should always be a little less than the grid bias voltage. As we have 1V bias, the peak input voltage should be less than 1V (700mV RMS). Any higher signal will cause grid current via the grid-cathode diode that's 'created' as a side effect. Grid current will cause input signal distortion, and may cause other problems depending on the worst case level.
A method for biasing (mainly high mu triodes or small signal pentodes) that used to be common is 'grid leak' or 'contact' (aka 'contact potential') biasing. It was common in early radio receivers when valves had directly heated cathodes (filaments), so cathode biasing couldn't be used. Using grid leak bias eliminated the need for the 'C' battery, which supplied a negative voltage to bias the valves in the receiver.
By using a very high value grid resistor and a coupling capacitor from the previous stage, stray electrons from the space charge surrounding the cathode are collected by the grid, and cause a voltage to appear across the grid resistor. This is also combined with the different 'work functions' ¹ of the cathode and grid materials. The grid resistor will generally be well over 1MΩ, and up to 10MΩ may be used. For example, if the grid collects (say) -100nA (nano amps) of current, a 10MΩ resistor will cause the grid to be at -1V referred to the cathode.
With normal cathode bias, the grid can be direct coupled to the outside world unless there are DC voltages present, but when grid leak bias is used there must be a blocking capacitor. This is because the grid will be at a negative voltage referred to the system ground, and any external connection would bridge the grid leak resistor and affect the valve's operating point. The coupling capacitor also stores the average voltage generated by the grid current.
In general, grid leak biasing is rather unpredictable, and is easily disturbed by a high level input signal. This can cause the valve to 'block' - basically switching off and preventing amplification until the grid capacitor has discharged back to normal. The blocking action happens when the input signal forces the grid to a positive voltage, and causes diode action between the cathode and grid to charge the input capacitor to the point where the valve is forced into cutoff (see note below).
There is no valid reason to use grid leak biasing any more, and it should be avoided.

Note: There are many explanations of grid leak bias (including some from otherwise 'reputable' sources) that state that the bias voltage is developed due to the signal voltage being partially rectified by the internal grid-cathode 'diode' (which conducts when the grid is positive with respect to the cathode). This is obviously nonsense - the valve will (must) be biased normally with zero signal. The bias voltage is (or should be) the result of a very small current flow between the cathode and grid and through a high value resistor, and must be present whether there is a signal or not. The DC blocking capacitor holds the charge constant as the signal level varies.
If the claim that signal is needed were true, the valve would be unbiased (and drawing maximum current) if no signal were present, and it would be unable to amplify normally until the signal had been present for up to several seconds (depending on the time constant of the input cap and grid resistor). Needless to say, this is not the case at all. As always, be wary of much of the info you find on the Net - myths tend to be perpetuated by repetition until they become accepted as 'facts'.
Be aware that there is also a circuit referred to as a grid leak detector. This is a different application of the grid leak principle, and it usually does rely on the input signal to develop some (but not all) of the bias voltage. The two systems are not equivalent in any way, and the operating principle and end-purpose are different. The grid leak detector relies on the non-linear operation of the valve to detect (rectify) an amplitude modulated radio frequency signal to recover the audio. The valve 'automatically' adjusts the grid bias depending on the amplitude of the RF carrier, and it provides reasonably high sensitivity over a wide range of available broadcast signal levels - some transmitters may be close by and others quite distant. It is not a form of AGC (automatic gain control).
It was mentioned above that an unbiased cathode resistor reduces the gain, so we can look at that now. The equivalent circuit has to be changed in order to simulate an unbypassed cathode resistor, but that won't be covered at this time. The following process can be used to determine the gain - while it appears complex, it's really quite straightforward ...
Av = µ × Rtot / ( rP + Rtot + ( RK × ( µ + 1 )))
Where µ is the amplification factor of the valve, rP is the internal plate resistance,
RK is the cathode resistor and Rtot is the parallel combination of RP (external plate resistor) and Rload.
For the example given above, we can work out the gain ...
Rtot = RP || Rload = 100k || 1 Meg = 90k
Av = 100 × 90 / ( 80 + 90 + ( 2 × 101 )) Note that the 'k' can be ignored, as it appears in all resistance values
Av = 9000 / 372 = 24
If you prefer, there's another method that gives the same answer, but the formula may be easier to remember ...
Rsource = rP + ( µ × RK )
Rtot = RP || Rload
Av = µ / (( Rsource / Rtot ) + 1 )
Av = 100 / ( 280 / 90 + 1 ) = 24
Note that the value of the cathode resistor is multiplied by the amplification factor. This extra (multiplied) resistance is then effectively added to rP. It's interesting that for this to make sense with an equivalent circuit, we have to use a voltage controlled voltage source instead of the VCCS used previously. Unlike transistors where everything makes reasonable sense and a single equivalent circuit is sufficient to explain everything, the operation of valves is more complex - largely because of their very limited gain.
There are many parameters that are listed for valves, and many datasheets include comprehensive performance graphs from which the designer can determine the best valve to use, the optimum plate current, required grid bias voltage, etc. During the golden years of valves, some makers published so much information that it was sometimes hard not to be confused. Others provided the bare minimum, but in all cases the necessary information was there - one simply had to look for it, and understand how it was interpreted.
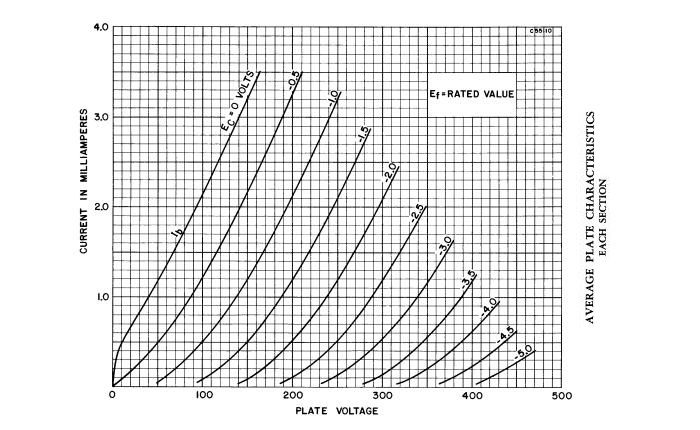
Now it's time to get serious. As noted above, there are quite a few graphs available for most valve types, so it can take a while to figure out which one to use. Some datasheets have no graphs at all, and while that makes life simpler, there are things that you don't get to know about. The average plate characteristics are always a good start though. From this graph, it's easy to see were the valve is most linear (look for the straightest line that extends over the widest range of plate current.
From the above graph, it's easy to see that the choice made for the examples above was less than ideal if there is any significant variation in plate current, such as for a high level amplifier (more than a couple of volts RMS). The greatest linearity is with a grid voltage of -0.5V, at a plate current of 2.2mA, requiring a plate voltage of 150V. However, there is a conundrum here ... high linearity over a wide range implies that we need a high output voltage, but given that the 12AX7 has limited gain, that also means the input voltage will be high too. If the input voltage exceeds 0.5V at any time, the grid will draw current (because it's positive with respect to the cathode).
Grid current is almost always a bad thing, and must be avoided in audio preamp or driver stages. When grid current is drawn, the input impedance of the valve falls dramatically, but only over that part of the input cycle where grid current flows. Distortion is therefore increased (equally dramatically) unless the source impedance/ resistance is very low. Since valves are high impedance devices, a low impedance source is difficult to achieve.
From the chart, it's easy to see that expecting high voltage drive with good linearity is not possible with a 12AX7 - a different valve must be used. This is why there are so many seemingly similar valves, such as the 12AX7, 12AU7 and 12AT7 (ECC83, ECC82 and ECC81 respectively), plus a great many others. Naturally, some people insist that there are huge differences in the sound of different valves, and to some extent this may well be true - depending on usage and accurate design procedures. One dual triode that does seem to be a cut above the average is the ECC88/ 6DJ8, but from what I've seen counterfeits are rife so it's probably best to steer clear unless you have 100% confidence in your source.
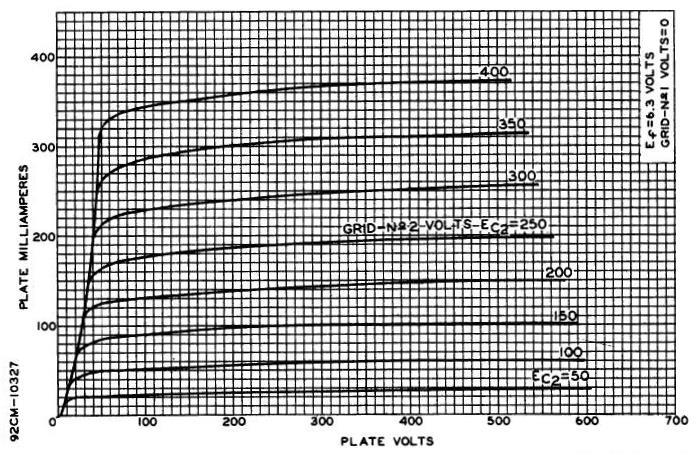
By way of comparison, the plate characteristics for a 6L6-GC (adapted from the RCA datasheet) are shown below. While the graph extends to 600V, the maximum recommended plate is 500V, and the maximum screen grid voltage is 450V. Maximum plate dissipation is 30W, although (and in common with all valves) this is the average value. If applied cyclically (as with an audio waveform), the plate dissipation will typically cycle between 60W and zero in use at maximum output.
Power valves are operated very differently from silicon (whether bipolar transistor or MOSFET). While they are far more rugged electrically (at least when new), they are fragile mechanically, and the mica supports start to break down with age, temperature and vibration. Even when power valves are used in strict accordance with the maker's recommendations, they have a finite life. In contrast, power semiconductors have an indefinite life, provided they are operated well within the peak limits described in the datasheets. They will fail if abused, but are not affected by vibration (as long as they are properly mounted of course).
Although output valves can be biased in exactly the same way as small-signal valves, this is usually only done with low power applications (no more than 15-20W output). High power amplifiers almost always use what's called 'fixed bias', where the control grids are connected to a suitable negative supply via suitable resistors. Drive transformers were used in early designs, but are ruled out by cost today. This is a topic unto itself, and guitar amp makers in particular have made some horrible mistakes with the bias supply.
There are a few things worth noting in the graph. Firstly, you can see that regardless of the stated plate dissipation, the valve will pass 300mA at a plate voltage of 400V and a screen grid voltage of 350V (120W dissipation). This remains one of the endearing things about valves in general - they can handle very high peak power without damage, provided the average remains within the upper limit. Even though valves in guitar amps are often pushed well beyond their ratings, they can still keep going for a surprisingly long time.
Any silicon-based device will fail under the same conditions. This is why it's possible to get at least 60W output from a pair of 30W valves, with transistors you need to allow for about 120W dissipation (each device) to achieve the same power. That's at 25°C, so you actually need more. For example, the Project 27 guitar amplifier uses 2 × 125W devices for the positive and negative sections (four transistors in all, 500W total dissipation at 25°C). Many early designers didn't understand this properly, so the designs were often unreliable.
The 6L6-GC has been included only as an example, but it's also worthwhile so you can see how to interpret graphs - and know what you can (or cannot) get away with!
Returning to small-signal valves, a useful formula that ties the three major parameters together is ...
gm = µ / rP
If two quantities are known, then the third can be worked out easily. This is handy, because not all datasheets provide all three parameters. It's also possible to get both gm and rP from the graph as shown above in Figure 3, so µ can be calculated. Let's do it ...
We know that gm (mutual conductance) can be in several forms, but we'll use mA/ Volt because it's sensible. We'll use the -1V grid load line, and simply pick a convenient plate current. 2mA looks good to me, and for 2mA, we need a plate voltage of 195V. Now, reduce (and increase) the grid voltage by 0.5V, moving to a curve either side of the -1V curve chosen. For the same plate voltage, the current increases to 3.15mA or decreases to 1.1mA - 2.05mA/ Volt. This is much greater than claimed, but is (more or less) within reason.
Plate resistance (rP) is determined by the change of plate current when plate voltage is changed, with the grid voltage held constant. Using the -1V grid voltage curve again, select a suitable plate voltage. 200V seems reasonable, and current is about 2.15mA. Select a higher plate voltage - say 250V. The current increases to 3.15mA, so rP is the change of plate voltage (50V) divided by the change in current (1mA), or 50k.
To calculate all the values (including µ) we use the following formulae ...
gm = ΔIP / ΔVG (Plate voltage maintained constant)
gm = 2.05mA / 1V = 2.05mA/ Volt
rP = ΔVP / ΔIP (Grid voltage maintained constant)
rP = 50V / 1mA = 50kΩ
µ = gm × rP
µ = 0.002 × 50k = 100
Note: The symbol Δ simply means the change between one measured value and another
We already determined that gm and rP vary depending on operating conditions, but that µ is a relatively constant figure. This has just been confirmed.
As alluded to earlier, the gain of a valve can be changed relatively easily. One method is to change the plate resistor, but this modifies the operating conditions so may cause excessive distortion. One can also load the output with additional resistance (after the signal coupling capacitor), but this is a pretty crude approach. The most common method is to partially bypass the cathode resistor, by using a resistor in series with the bypass cap.
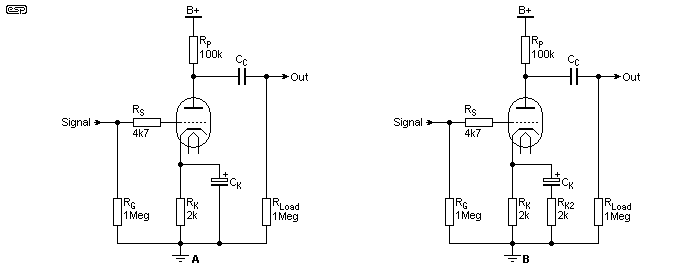
The first circuit shown ('A') is the normal arrangement, where the cathode is fully bypassed. As calculated above, this gives a gain of 53, which may be too high. By introducing a resistor in series with the bypass cap (RK2), the gain can be adjusted to anything between the gain with no bypass at all (calculated above at 24) to the maximum of 53. To make a change outside this range, either choose a different valve or modify the operating conditions (a smaller plate resistance for example).
With a 2k resistor as shown in 'B', the total resistance for AC is 2k || 2k, which is 1k. Gain can be recalculated using this value, and most importantly, the operating conditions of the valve are unchanged.
Rsource = rP + ( µ × RK )
Rtot = RP || Rload
Av = µ / (( Rsource / Rtot ) + 1 )
Av = 100 / ( 180 / 90 + 1 ) = 33
Whenever a cathode bypass cap is used, we need to determine the value needed. The impedance at the cathode is not simply the value of RK, but includes the impedance of the cathode itself. When looking inwards towards the cathode (as opposed to its effect internally), the impedance is ...
rK = ( Rload + rP ) / ( µ + 1 ) Where Rload is the parallel combination of the anode load resistor and the load impedance
Using the same conditions as before, we get ...
rK = ( 90k + 80k ) / ( 101 ) = 1.63k
For the 'A' circuit, the cathode resistance (rK) is 1.63k, the external resistor is 2k, and the parallel combination works out to about 890 ohms. The bypass cap must be determined for that value. For both circuits, the cathode bypass cap must have a low reactance at the lowest frequency of interest, and for 'B' we have an impedance of 2k in series with 890 ohms, or 2.89k ohms. It is traditional with valve (and most other) circuits to make the capacitor at least 5 times larger than required, so for a minimum frequency of 20Hz, the minimum capacitance needs to be ...
C = 1 / 2π F R
C = 1 / 2π × 20 × 820 = 8.94µF
C = C × 5 = 44µF (use 47µF)
For the fully bypassed version ('A'), the cap needs to be at least 47µF. There are many good reasons to make CK even larger, and a value of 220µF is not at all unreasonable, and in fact, that would be preferable. Electrolytic caps are essential because of the large values needed, and these are renowned for having wide tolerance and losing capacitance as they age (especially at the elevated temperatures in a valve amplifier). When a series resistance is used (as shown in 'B'), the total cathode impedance is calculated as before, and the value of RK2 is simply added to that. For our example, the total impedance is 890 + 2k, or 2.89k. The capacitance value needed is reduced accordingly (the minimum is about 15µF).
Be careful if the cathode resistor is left completely unbypassed. This can sometimes lead to a large and unexpected noise increase. The resistor should be of high quality and low noise - metal film is recommended. Also, any heater-cathode leakage can cause the valve to amplify the small leakage current, leading to much higher background hum levels. If unbypassed cathode resistors are used, ideally the heaters should be operated from (smoothed and preferably regulated) DC.
All valve stages have an input and output impedance (like all electronic circuits). The input impedance is almost always simply defined by the value of the grid resistor (often referred to as a 'grid leak' resistor, but grid-leak biasing is something completely different - see Section 3.1 for details). The valve itself is thought to have an almost infinite input impedance, but that's not strictly true. Input impedance is affected by grid current, and in a non-linear manner. Even when biased normally, a small grid current will flow that affects the impedance, and Miller capacitance between plate and grid causes the input impedance to fall at high frequencies.
Output impedance is more complex again. It is the parallel combination of the valve's internal plate resistance, the external plate resistor and the following load. Miller capacitance causes negative feedback at high (audio) frequencies, which slightly reduces the effective impedance of the valve itself. In many cases, the following load will be an unknown, so traditionally it is not included. For the example we've been using, output impedance (simplified) is therefore ...
Zout = rP || RP
Zout = 80k || 100k = 44.44k
When determining the value of the coupling capacitor, the impedance of interest is the total impedance in series with the cap, and assuming a 1MΩ grid resistor on the next stage, we get ...
Z = ( rP || RP ) + Rload
Z = 80k || 100k + 1M = 1.044M
The minimum capacitance needed is therefore 7.6nF for a -3dB frequency of 20Hz. For coupling capacitors, it is generally wise to increase the value by between 2 and 5 times, making the optimum value between 15nF and 39nF (or 47nF if you prefer). When the output is sent externally (to a separate power amplifier for example), the output impedance needs to be as low as possible.
A cathode follower (or a high voltage MOSFET source follower) should be used to ensure the output impedance is low enough to drive the external amplifier and the interconnect lead capacitance. Note that the following stage must be protected against high voltages if a MOSFET is used, because the output will jump to the full supply voltage when power is applied and before the valve has warmed up.
Finally for this section, we have to look at the internal capacitance between the grid and plate. For the 12AX7, this is specified at 1.7pF. In some of the original datasheets, the term µµF was common. This implies one millionth of one millionth of a Farad, which is one picofarad (pF). Awkward and outmoded, and not mentioned further. Even worse was mmF, where 'm' was used to indicate 'micro'. This terminology is still used by some people to this day, which is most regrettable.
Given that there's a capacitance of 1.7pF between the plate and grid, this provides a feedback path for high frequencies. The situation is made worse, because this capacitance is multiplied by the stage gain, so with a gain of 53 (as determined at the beginning), the small CP-G capacitance has grown to 90pF - this is known as the Miller capacitance. If we had an identical stage driving the one we're looking at, this 90pF in conjunction with the output impedance of the preceding stage (plus the value of the grid stopper resistance if significant) will cause a high frequency -3dB frequency of 36kHz ...
R = Rout + RS
R = 44.44k + 4.7k = 49.14k
F-3dB = 1 / 2π R C
F-3dB = 1 / 2π × 49.14k × 90pF
F-3dB = 36kHz
If a better high frequency response is required, the options are to reduce the gain of the stage in question, reduce the source impedance, add some negative feedback around the whole stage (uncommon), or use a different valve with lower plate to grid capacitance. For most applications, the limited HF response is usually not a problem, either because there is no need for extended response (guitar amps for example), or because very high gains are not needed. In some cases, there is no alternative but to use a pentode, where the screen grid isolates the control grid from the plate, reducing capacitance dramatically.
Remember too that the Miller capacitance of the valve itself isn't the only thing that can reduce the HF response. Because valve amplifiers have relatively high impedance and many are hard-wired, stray capacitance can also be a problem - especially if plate and grid components are physically close to each other. Wiring practices are critical in high impedance circuits, both to prevent HF rolloff and minimise hum and noise.
No article of this nature would be complete without some photos, so here they are.

These types represent some of the more popular valves, although the 12AT7 and 6L6GC are notable omissions because I don't have any to photograph. Fortunately, there are copious photos of valves on the Net, so no-one should feel deprived. As always, inclusion of a visible branding does not imply any affiliation or recommendation for the brand shown. In some cases, quite the reverse is true, but I have no intention of making any comments one way or another, because the quality of the valves available from any maker or reseller can be highly variable - good today, useless tomorrow.
There is a significant amount of work needed to design well behaved valve preamp (and output) stages. While a working design is easy - just copy what someone else has done or dream up a few likely values - getting it right takes time and effort. Valves are fairly forgiving ... you have a large supply voltage to play with, most valves work (i.e. do something more or less useful) over a very wide range, and getting a stage that refuses to function at all is actually difficult (other than wiring mistakes of course).
Understanding the interactions and actually designing the circuit is very time consuming, so it's no real surprise that many people just don't bother. There are so many circuits on the net that what appears to be the exact one you need is easily found. However, the interaction between stages, comparatively high output impedance and optimum linearity for an application are difficult to work out, and it's often easier to build it and make modifications as needed. It's also worth noting that many of the 'classic' circuits were often rather poorly thought out (especially with guitar amplifiers). That they happened to give a sound that guitarists liked was almost an accident - there are many examples of very, very poor application of valves in some of the most famous guitar amps made, and some major (and very serious) errors persist to this day. In some cases, the poor design just happens to provide the sound that guitarists like, so if very short valve life is the price you pay for 'the sound', then so be it. In other cases, there is no excuse for some of the blunders made. It's well known that early Marshall guitar amps were a direct copy of the original Fender Bassman, and this is possibly one of the most blatant direct copies, but almost certainly there are others too. It shows that even manufacturers will copy other circuits (warts and all) as readily as hobbyists.
One of the difficult aspects of valve design is to determine the optimum operating point that gives the required gain with the minimum distortion. Perhaps surprisingly, this can become especially critical for cathode followers. While a cathode load of (say) 47k might seem perfectly reasonable, during some experiments for this article I have seen the distortion fall by almost 20dB simply by changing the load to 10k. However, this involved a major trade-off, in that a circuit that could output over 20V RMS easily (but with relatively high distortion) was unable to reach 10V RMS before distortion rose alarmingly (well above the previously measured level). At lower levels (around 3V), the distortion fell from about 0.8% to slightly less than 0.1% - simply by changing the load impedance. While valves may be forgiving to get a working amplifier stage, they are far less so when you want to get the lowest distortion performance from the stage.
The high quality audio equipment from the likes of Leak, Quad, McIntosh and others was generally very well thought out, and everything was done for a good reason. Some used very complex transformer configurations to get the best possible performance. Not so the consumer equipment that came from (mainly) Japan towards the end of the valve era. Some of the designs were between being very ordinary and appalling, and to call the wiring 'rough as guts' was actually high praise. Obviously, there were exceptions, but I can't think of any at the time of writing. For all of that, they worked pretty well, and did (more or less) what was expected of them, but when transistors came along these products died away almost immediately. Transistor circuits produced more power, mostly - but not always - lower audible distortion, much less heat, and (probably most importantly) were cheaper to make. Power supply requirements were simpler, and as a result hi-if valve equipment all but died until the 1980s when we started to see a resurgence of designs - some using pre-WW II technology which may have considerable 'magic' appeal, but are fundamentally worthless.
If a valve amp were to be designed now, the only sensible output valve choice for an amp providing a useful output power would have to be the KT88/ 6550 or preferably, the KT90. These are less common, and are actually a completely new type having been introduced in or around 1990. These have proven to be far superior to KT88s in a collaborative design done by John Burnett and myself. Attempting to use really old valves (such as the 300B for example) might get a working amp, but performance will not be up to the hi-if standards that are accepted today. Not that there's anything wrong with the 300B - in its day it was one of the best power triodes available, but that day was a very long time ago. Single ended designs are simply an abomination compared to the alternatives, and serve no useful purpose.
For output stages, it was determined by the best engineers of the valve era that push-pull was the only viable option for a high quality amplifier. With no net DC component flowing in the output transformer primary winding, it was far easier to make the transformer to a high standard, with much lower losses and performance that could not be matched by any other topology. Nothing has changed today, and a push-pull output even allows the use of a toroidal output transformer. With lower leakage inductance than any other type of transformer, use of a toroidal core can improve bandwidth to an extent not considered possible previously.
Towards the end of the valve era, there was even a brief period where transformerless (OTL - output transformer-less) valve output stages were built. Some required loudspeakers with high impedance voicecoils that proved impractical, and required almost impossibly large inductances for any crossover network. Efficiency was dreadful, and special valves were needed. Altogether a bad idea, but part of the evolution of hi-if as we know it today.
It is inevitable that errors will creep in during the compilation of information, and these are regretted in advance. If any such errors are found, please let me know.
 Main Index Main Index
 Valves Index Valves Index
|