

|
| Elliott Sound Products | Project 170 |
There are already plenty of active crossover designs on the ESP site, so one more is either complete overkill or potentially useful. I leave it to the reader to decide. In general, 6dB filters are one of the best possible for any speaker system. They allow a squarewave to pass unadulterated (if properly set up of course), and being rather gentle, they do nothing 'bad' to the signal.
However, bear in mind that very few loudspeaker drivers will be happy, because they will all get significant power at frequencies well outside their 'comfort zone'. This can allow cone break-up effects to become audible, and does nothing to suppress the natural resonance of the driver. These factors have dictated that most manufacturers of tweeters (in particular) rate the 'system power' with a 12dB/ octave filter, and as a great many constructors have found, using 24dB/ octave eliminates many of the most troublesome frequencies quickly enough that the overall result is generally superior to lower order filters.
Accordingly, the majority of the circuits described on my site are a minimum of 12dB/ octave, with a couple of 18dB designs just to ensure that the line-up is complete. For most serious listening, I have recommended the P09 24dB/ octave filter, and many hundreds have been built with pretty much universal agreement that this is by far the best arrangement. 6dB/ octave filters gave been largely (but not completely) ignored, so that will be set to rights forthwith. 
Because of the very slow rolloff slopes involved, it may be necessary to add notch filters to suppress resonant peaks from the midrange and/ or tweeters. Higher order filters remove most of their effects, but a first order filter cannot do so effectively. Drivers should ideally have a response such that resonance is at least two octaves below the crossover frequency. For example, a tweeter with a 1kHz resonance should not be used with a crossover frequency less than 4kHz. Even with this apparently large safety margin, the tweeter output will only be about 12dB down, and may receive significant power at its resonant frequency.
In common with all active crossover networks, there is no requirement or necessity to use impedance correction networks on any of the drivers, because each is driven directly from its own amplifier.
A 6dB/ octave active filter will use resistors, capacitors and buffers. Inductors will not be shown, although they can be used. However, the inductor is by far the worst passive electronic component known, having far more of the other two (resistance and capacitance) than resistors or capacitors. There are some who believe (but cannot prove it in any meaningful test) that capacitors are somehow 'bad', but this is an opinion, and the facts are very different.
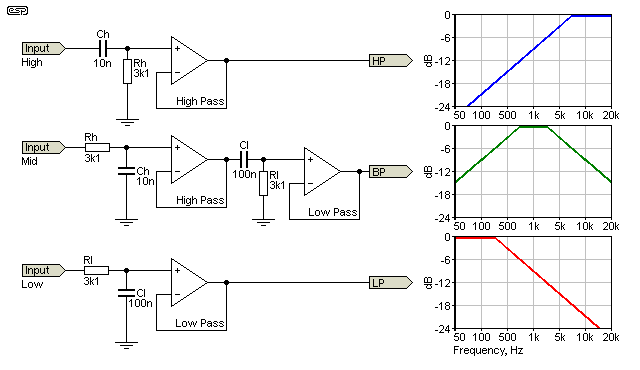
Figure 1 - Basic High Pass, Band Pass And Low Pass Filters
The three filters shown above are the simple building blocks, and you can (at least in theory) use as many bandpass sections as you like. However, because of the slow rolloff slope of 6dB filters, more than three sections is uncommon, and four is generally as many as can ever be used. Fortunately, we rarely need more than four sections for a crossover, so that isn't an issue. One thing that's readily apparent is the slow rolloff. Each filter is 3dB down at the design frequency, and the response curves shown above are 'idealised'.
In reality, the turnover point is not sharply defined, and the actual response of a 4-way filter is shown further below. The frequency for any of the filters is determined by the standard formula ...
f3 = 1 / ( 2π × R × C )
(Where f3 is the -3dB frequency, π is 3.1416, R is resistance in ohms and C is capacitance in Farads)
As shown, the frequencies are 513Hz and 5.13kHz. If you are unsure why the buffers are needed, look at the filter sections, and imagine how they will be affected when loaded by an external circuit or another filter. The opamps have extremely high input impedance when used as buffers (if you use FET input opamps the input impedance is effectively close to infinite). This prevents the following circuitry from changing the filters' insertion loss and frequency response. Each filter has to be driven with a low impedance, or performance is affected again. The sections shown above are assumed to be driven from zero impedance, but in reality it will always be up to a few ohms from typical opamps. This causes a small error, but it's negligible in practice.
Resistors will ideally be between 2.2k and 22k to limit thermal noise and to keep capacitors within reasonable limits. Values less than 1nF or greater than 220nF should be avoided if possible, because with very low values stray capacitance causes problems, and opamp loading becomes too great with high values. The range of resistors and capacitors has more than enough flexibility for any desired crossover frequency. Do not use 'high k' ceramic (multilayer, SMD, etc) caps for the filters, because they are unstable with temperature and have high distortion with even modest audio levels.
A fully working circuit isn't much different from that shown above. You must have an input buffer to ensure that all filters have a low source impedance, and each filter section is buffered as well. The input buffer may need to be able to drive quite low impedances, so use an opamp that can drive 600 ohms (NE5532, OPA2134, LM4562 or similar). The outputs are via 100 ohm resistors to ensure that the opamps remain stable with capacitive loads (especially from shielded cable interconnects).
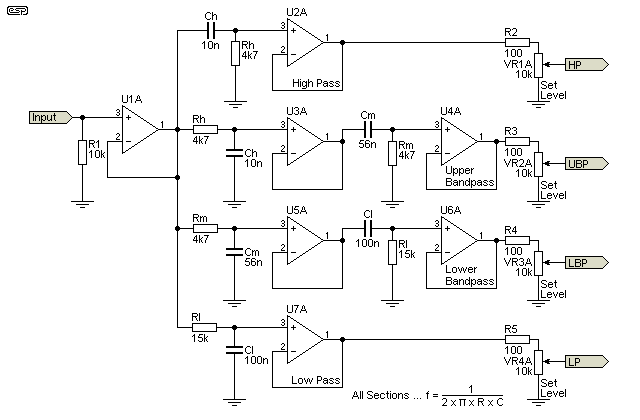
Figure 2 - Full 4-Way Electronic Crossover Network
You can use any competent opamps for the individual buffers shown. As is usually the case, I've assumed dual opamps, and the 'B' half is used for the second channel. Quad opamps can also be used. You can add or remove bandpass sections, making sure that you calculate the proper component values for the frequencies needed in your application. For the bandpass sections, I've shown the high pass filter first. You can have the low pass section first if you like - it make no difference to the way the filters work. In the graph below, the red trace is the sum of the four outputs. It's reduced in level so you can see it clearly.
If you need more (or fewer) bandpass sections, you can work out the values needed yourself. The sequence is shown above, with 'Ch' being the high pass capacitor and 'Rh' being the resistor. The same nomenclature is used for all filters. For a 4-way system, there will be 3 different sets of resistors and capacitors. Only two sets are needed for 3-way, and one set for a 2-way network. The crossover frequencies for the network shown are 106Hz, 605Hz and 3.38kHz. The level controls allow you to set the gain for each frequency, because the drivers will not have identical SPL (sound pressure level) for the same input power.

Figure 3 - Frequency Response of 4-Way Crossover Network
Perhaps surprisingly, when the four signals are summed the response (red trace) is not completely flat. There is a slight rise across the midrange region, because the slow rolloff slopes allow more signal to get through. This causes a rise of about 1.6dB and although it's real, it is of no consequence in reality. The trend is visible on the graph, and the peak is at 485Hz. Equally surprisingly, the summed output is capable of reproducing a squarewave quite well (it's modified a little due to the 1.6dB rise in the midrange). This isn't shown, so you'll have to take my word for it.
Is the ability of a filter to pass a squarewave actually important? In a word, "no". There has been much discussion about the audibility of phase, and the consensus of those who have actually performed properly conducted blind tests is that phase shift (within sensible limits of course) is not audible. Those who claim otherwise will have come to their decisions with sighted tests, where they already know what they are listening to. This instantly makes the test worthless, and the results are of no value whatsoever.
Even if the crossover can pass a squarewave (after summing), when the acoustic signal from the speakers is summed it's almost guaranteed that the squarewave will be mangled by the phase shift of the drivers, compounded by the time shift that occurs if the acoustic centres of the drivers are not in perfect alignment. This is harder than it sounds, because the acoustic centre of most drivers changes with frequency.
There will no doubt some constructors who would prefer that the inputs and outputs be balanced. If this is the case, use the circuits shown below. The balanced input stage is a common circuit, and while some believe that it's not especially good, that's actually not really true. However, feel free to use one of the more complex versions of course - see Project 87 for details and examples. The balanced input has unity gain.
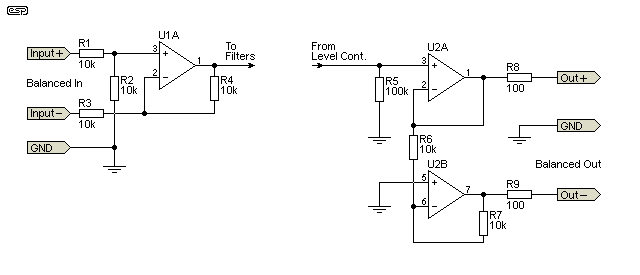
Figure 4 - Balanced Input And Output Circuits
The balanced outputs require one of the circuits shown for each output, and they have an effective gain of two, because the signal is provided 'straight through' and again inverted by U2B. If you build a 4-way crossover, you need four balanced outputs for each channel (left and right) - eight in all. Again, there are alternative circuits in the page referenced above, but there is almost never any good reason to use a more complex circuit. You can also use transformers for input and output, but this is a very expensive option.
There is little or no chance that a dedicated PCB will be offered for this project, because it's not suitable for the vast majority of systems. If anyone really wants to build it, the P09 board could be adapted easily enough - it's simply a matter of leaving out most of the parts. Two P09 PCBs are needed for a 3-way system, and you'd need 4 boards for a 4-way. P125 could also be used, and again that means leaving out most of the parts and installing links to bypass the unused opamps (also required with P09).

| This is the layout of dual opamps, viewed from the top. The pinouts shown here assume the use of a dual opamp in each location. Pin 4 is the negative supply, and pin 8 is positive. In all cases, you must use a 100nF multilayer capacitor close to the IC and across the supply pins. Many opamps will oscillate if this is not included. You will also need similar caps from each supply to ground, but this is only needed at one position on the board, typically at the supply input. |
For those who don't want to use a partially-populated PCB, you can make the circuits up easily enough on Veroboard or similar. The layout isn't critical, but the filter circuits should be close to the opamps to minimise stray capacitance which can be a problem if low value caps are used. Resistors should be standard 1% metal film (0.25-0.5W). Capacitor values are usually 5% tolerance at best, so you can select the caps using a capacitance meter if you like. However, even 5% caps will be quite sufficient, because the filter slopes are so low that a small error is of little or no consequence.
There's really not much more to say about this project. It's unlikely to be suitable for the vast majority of systems, but high-efficiency systems using horns may work reasonably well, because the horns themselves add some rolloff (horns are effectively bandpass filters in their own right). The biggest issue is always going to be excessive power being delivered to the high frequency driver. Tweeters (whether direct-radiating or compression drivers) do not like getting appreciable power below their recommended crossover frequency. They generally show their displeasure by failing, but at lower powers you may hear resonance artifacts or other effects.
Low and mid frequency drivers may suffer cone breakup if driven to higher than optimum frequencies. This is usually audible, and rarely sounds good (to put it mildly).
Some people may believe that opamps "don't sound any good" and might prefer to use a fully discrete solution for the buffer stages. This isn't something I will ever advise, because no discrete buffer that doesn't use a very complex circuit can even approach the performance of even pretty basic opamps. However, if you do want to make up a large number of discrete buffers, some examples are shown in the article Follow The Leader - Voltage Followers & Buffers.
Otherwise, it's a project that some people may find useful, and if nothing else it gives you options that aren't readily available elsewhere. You may also simply want to put one together just for fun - this isn't as silly as it might sound. Many of my regular readers do build projects because they want to see how they work, but with no immediate use for the finished item.
 Main Index
Main Index
 Projects Index
Projects Index