
 |
| Elliott Sound Products | How Fluorescent Lamps Work |
 Main Index
Main Index
 Lamps & Energy Index
Lamps & Energy Index
The article Traditional Fluorescent Tube Lamps & Their Alternatives looks at the operation of fluorescent lamps in fairly simple terms, but here we will examine the lamps, their ballasts (both 'traditional' magnetic and electronic types) and delve a little deeper into their inner workings. There are alternative ballast schemes used (such as the 'lead/ lag' arrangement) and this is shown in the previous article. It's not covered here, because this is about how they work, rather than a discussion of the way fittings are wired.
The way a fluorescent lamp works is very different from a simple incandescent lamp, and modern fluorescents (especially the compact fluorescent lamp, or CFL) make use of electronic ballasts to regulate the voltage across the lamp, and the current through it. When first started, it is necessary to provide a significantly higher voltage than normal to cause the internal arc to strike, and once started, the current must be limited to a safe value for the tube.
This article shows some of the ways these goals are achieved, starting from the basic inductive ballast that has been the mainstay of fluorescent lamp production for many years.
Note that the waveforms shown here are a combination of simulations and actual measurements. Where necessary, the simulated waveforms are corrected to match those measured. The reason for this approach is simple ... the simulator cannot represent a negative impedance load with appropriate strike voltages and other characteristics that a fluorescent tube presents. Likewise, it is very difficult (and potentially lethal) to attempt to capture all the voltages and currents that exist in real fluorescent lamp circuits.
While the approach taken does introduce some minor errors in the waveforms shown, these are relatively insignificant, and the end result is well within any traditional manufacturing tolerance for ballasts, lamps and other components.
For the inductive ballast explanations, I used an old 'compact' fluorescent lamp, which just happens to be ideal for testing. Although it still works, light output is somewhat below what it should be, but that only changes some of the measured values a little. The principles are not changed at all.
The lamp itself has the following characteristics ...
Tube Diameter 11.3mm (non-standard) Length 533 mm (21") Filament Resistance (cold) 12.8 Ohms Filament Resistance (hot) 23 Ohms Ballast Resistance 105 Ohms Ballast Inductance 2.11 H Starter Conventional Neon Starter Capacitor 1.2 nF
The diameter of fluorescent tubes is commonly referred to as T8 (for example). This means that the diameter is 8 x 1/8", which is 1" (25.4 mm). Early tubes were T12 (1½" or 38mm diameter), but these were reduced in size to T8 when the (then) 'new' high efficiency types were introduced. a standard 4' tube (1,200mm) used to be rated at 40W, but their replacements were 36W and light output was improved. The latest incarnation is the T5 (16mm diameter), which uses a smaller pin spacing and a different tombstone fitting. They are also shorter (1,163mm) and will not fit into a standard luminaire designed for earlier tubes.
In the case of my test unit, the tube diameter is much smaller than normal because the lamp is designated as a compact, so it is folded to reduce the overall length. Filament resistance is mentioned because it will be referred to later in this article. The schematic is shown below, and is conventional in all respects.
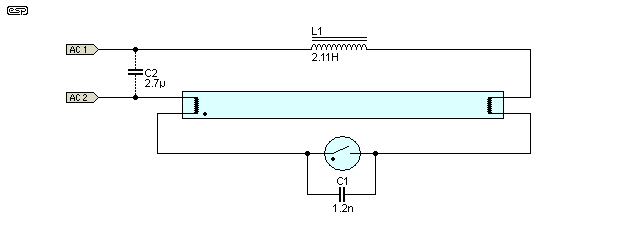
Figure 1 - Fluorescent Lamp Schematic
The inductor is the ballast, and is actually a far more important component that it might appear. It not only limits the maximum tube current, but is used to generate the high voltage pulses needed to start the plasma arc within the tube. The fluorescent tube tube itself has a heater at each end, a small quantity of mercury and an inert gas (usually argon). The wall of the tube is coated with phosphors that emit visible light when excited by the intense short-wave ultra-violet light emitted by the mercury arc discharge. The extra capacitor (C2) is for power factor correction - more on this later.
The small bulb is the starter. A bimetallic strip is sealed into a glass envelope, with (usually) neon gas inside. When power is applied, the voltage is more than enough to cause an arc in the neon starter, but nowhere near enough to start the arc in the lamp itself. The heat from the neon arc causes the bimetallic strip to bend, until it closes the contacts. The arc in the neon starter then stops, and the mains is connected through the ballast and the filaments at each end of the tube, via the starter switch.
Once the starter has no arc (or glow), the bimetallic strip cools, and the switch opens after about a second or so. The interruption of current through the inductor causes a voltage 'flyback' - a high voltage pulse that will (hopefully) start the arc in the tube. If the arc does not start the first time, the process repeats until it does. This is why standard fluorescent lamps flicker a few times when switched on. The filaments are heaters that act as cathodes (emitters of electrons), and are needed to ensure that there is enough heat to vaporise the mercury, and to get a good electron flow to energise the plasma. Once the lamp is working normally, the electron flow is enough to maintain the filaments at an acceptable operating temperature. Both filaments act as cathodes and anodes alternately, because the polarity reverses 50 (or 60) times a second.
The plasma has an interesting characteristic ... negative resistance! Once the arc starts, a higher operating current causes the resistance to fall, and less voltage appears across the tube. If this were allowed to continue, the tube would destroy itself very quickly. The ballast prevents this from happening because it introduces a series impedance to limit the current. Resistance will not work, because it is too wasteful, and provides no energy storage to generate a flyback voltage spike to re-strike the arc with each polarity reversal.
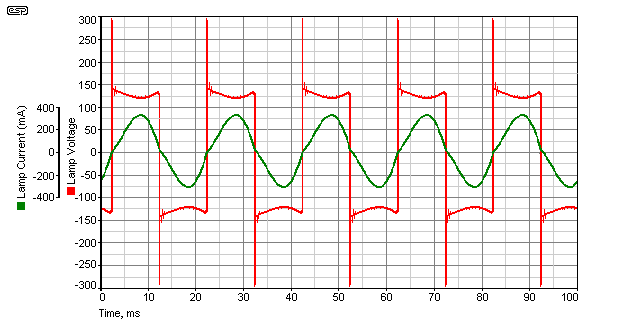
Figure 2 - Operating Waveforms
In Figure 2, you can see that when the tube current (green trace) is at the maximum, the voltage (red trace) across the tube is a minimum. You can see the effect just after each voltage spike. As current goes up, the voltage falls (for this tube, the minimum was ±126V). The spike at the zero crossing point of the current waveform is generated by the ballast, and it is this that re-ignites the arc for each half-cycle of the applied mains. Figure 3 shows the voltage across the ballast - the rapid transitions correspond to the spikes applied to the lamp, and occur near the peak of the voltage, where the current is interrupted as it passes through zero.

Figure 3 - Voltage Across & Current Through Ballast
The voltage waveform across the ballast is essentially the difference between the applied mains voltage and that across the tube. For 120V operation, the voltage is obviously less, but the tube still needs somewhere between 300-400V to strike (or re-strike) the arc, so the ballast has to be able to make up the difference with a flyback pulse at each zero-crossing of current. I don't have a 120V fluorescent lamp or ballast available, so I'm unable to provide full details. That fluorescent lamps even work at all with 120V is somewhat remarkable, but it's easy to see why electronic ballasts are so popular in the US. Many ballasts for 120V countries use an auto-transformer 'ballast' that increases the available voltage and acts as a current limiter.
There are several losses in the system, with the ballast being one of the major contributors. The ballast used for my tests has a DC resistance of 105 Ohms, so wastes almost 7W. The loss is actually higher, because the steel laminations get hot very quickly, so 'iron loss' is considerable. This can only be reduced by using better quality steel and thinner laminations. Both will add considerably to the cost.
Each filament has a hot resistance of 23 Ohms, and a voltage of almost 6V is present across each filament when the lamp is operating. Remember that when running, the end of the filament that goes to the starter is disconnected (except for the very small capacitance across the starter). The voltage measured is a gradient caused by the plasma current, and each filament dissipates about 1.5W (3W total). Just in these components, the fluorescent lamp wastes 10W of the applied power as heat (7W for the ballast, 3W for the filaments).
While the ballast waste can be lowered with a higher quality unit, the filament loss is necessary for the lamp to function. This applies with all fluorescent lamps except specialised cold cathode types, but they require an equally specialised electronic ballast. CCFL (cold cathode fluorescent lamps) are (were) most commonly found in LCD monitors and TV sets but are now replaced by LEDs in new models.
There is another loss which isn't seen or even paid for by the user. This loss is the result of the poor power factor of fluorescent lamps, and this is caused by the predominantly inductive load. The inductive load causes a lagging power factor, where the maximum current occurs after the maximum voltage. You can also consider it as a point where the load (the lamp and inductor) actually return some power to the supply. For the electricity supplier, this means that transformers, cables and alternators have to be capable of more current than should be the case. This becomes very costly when a great many loads have a poor power factor.

Figure 4 - Voltage Vs. Current, Uncorrected and Corrected
In Figure 4, you can see that the uncorrected current waveform has visible distortion near the zero crossing point. As you can also see, the RMS current is also significantly higher than the power rating would indicate. Reactive loads have different power and VA ratings, but for a resistive (or non-reactive) load they are the same.
In this case, the current without C2 is 256mA, and when C2 is added it drops to 162mA. At an applied voltage of 240V, this means that ...
Uncompensated Total Power = 38W VA = 61.4 Power factor = 0.62 Compensated Total Power = 38W VA = 38.9 Power factor = 0.97
Power factor can be calculated using the phase delay or by dividing actual power by VA ( Volts * Amps ). For phase angle, the current lags the voltage by 57.4°, and power factor is calculated by taking the cosine of the phase angle - 0.53 in this case. The figures are different, because the current waveform is not a pure sinewave - it has distortion. Adding the capacitor shifts the phase of the distortion so the compensated current waveform gets a flat top (somewhat like an amplifier clipping). Although this does introduce harmonics into the mains system, the effects are nowhere near as bad as the uncompensated circuit as evidenced by the corrected power factor. Adding a capacitor of the correct value to a purely inductive circuit (with no waveform distortion) will give a power factor of unity - the ideal.
 | Note that using the cosine of the phase angle ( CosΦ) is a shortcut, and can only be used when both voltage and current are sinewaves. It does not work at all for highly distorted waveforms such as those produced by electronic loads, and will give an incorrect answer for inductive loads that include distortion (such as fluorescent lamps). You will always get the right answer if you divide real power by VA. |
There are also 'quick start' and starterless ballasts available. These are beyond the scope of this article, which is intended to describe the basic principles rather than an in-depth coverage of every fluorescent lighting ballast available.
Electronic ballasts are becoming far more common, because they can be made to be more efficient than a typical magnetic ballast, and they require far less material. This makes them cheaper (to make, though not necessarily for you to buy) than fluorescent lamps using a conventional ballast. Compact fluorescent lamps (CFLs) in particular now all use an electronic ballast, and it is commonly supplied with the lamp itself. Although convenient, this is a dreadful waste of resources, because of all the electronic parts that are simply thrown away when the lamp fails. T5 tubes are now becoming the standard for fluorescent lighting, and for maximum life an electronic ballast is mandatory.
To some extent, the efficiency improvement over a magnetic ballast may be an illusion - at least in part. Because they are much lighter, there are real and definite savings in transportation costs, but magnetic ballasts can be made to be just as efficient as an electronic version - perhaps even more so. Be that as it may, the swing to electronic ballasts cannot be stopped now, and as the price comes down usage will continue to increase. Electronic ballasts have some other advantages too, and these will be discussed later.
A (more or less) typical circuit diagram of an electronic ballast as used in a CFL is shown below. Those used for conventional fluorescent lamps will be very similar, but will generally use upgraded components. While the electronics in a CFL may only have to last 15,000 hours, a fixed electronic ballast will be expected to last perhaps 100,000 hours or more (over 10 years continuous operation). In reality, an electronic ballast should be able to last as long as its magnetic counterpart, so a 40 year lifespan is not as silly as it may sound.

Figure 5 - Electronic Ballast Schematic [2]
The schematic in Figure 5 is a slightly simplified version of that shown in the Infineon data sheet. It is fully power factor corrected, and has protection to detect faulty (or missing) lamps. A characteristic failure mode of fluorescent tubes is 'rectification', where one filament (cathode) becomes significantly weaker than the other. If not detected, the DC offset will cause the switching devices to fail, rendering the ballast useless (it is highly unlikely that anyone will repair them when they break down).
The electronic ballast does have some real advantages over the magnetic version. Because the arc will fully extinguish in around 1ms, by using a higher frequency than the 50 or 60Hz mains, the arc will remain. It does not need to be re-struck, but simply reverses direction [1]. In addition, light output is increased by around 10% above 20kHz, so the luminous efficacy is improved.
Until such time as all of these electronic ballasts are power factor corrected, they will cause problems with distribution. Unfortunately, in many countries there is no requirement for low power (typically less than 75W) appliances to have power factor correction, but given the proliferation of CFLs and electronic ballasts in conventional fluorescent lamps this will have to change. Since lighting is used in every household, the problems of uncorrected power factor will get out of hand if something isn't done.
Unlike a magnetic (inductor) ballast, an electronic ballast cannot be power factor corrected by simply adding a capacitor. As seen in the diagram above (although it may not be immediately apparent), there is only a very small capacitor of 220nF across the output of the input bridge rectifier. The first MOSFET operates as a boost converter, and switches right through each half cycle. By doing so, the RMS current drawn from the mains is maintained in phase with the voltage, and the current waveform is approximately sinusoidal. This gives a very good power factor - better than 0.9 is possible. In order to prevent the high speed switching pulses from getting back into the mains supply, extensive filtering is needed, as indicated by the EMI (electro-magnetic interference) filter at the input.
A somewhat simpler scheme is used for compact fluorescent lamps (CFLs), as the circuitry is designed to be thrown away. Personally, I consider this to be wanton waste, and hope that it doesn't continue (or at least recycling is put in place to recover as much as possible). A reasonably typical CFL inverter is shown below ...
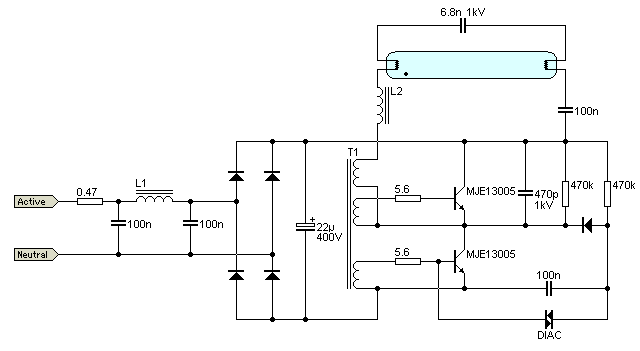
Figure 6 - Typical CFL Electronic Ballast Schematic
I say "reasonably typical" because there are wide variations in the actual circuits. There are dedicated MOSFET driver ICs available, but most of the cheap (consumer grade) CFLs will use a variation of the above. Note that the 0.47 Ohm resistor shown at the input is usually a fusible resistor, and it is used a a fuse first and foremost. Why not use a real fuse? Resistors are cheaper. Most of the parts will be selected to survive for the designated life of the lamp, so best design practices are typically ignored if a lower rated (and cheaper) part can be expected to survive for 10,000 hours or so.
The transformer (T1) is there to provide feedback to the transistors, and generates the base current needed to ensure reliable switching. The cycle is initiated by the DIAC - a bidirectional device that has a sharp transition from the non-conducting to conducting state. Because it shows a characteristic very similar to a negative impedance device it is a common part in light dimmers, fluorescent ballasts and even strobe lights. For more information, click here for a DIAC tutorial.
Please note that the circuits shown above are for information only, and must not be built as shown. Some components require very specific ratings, transformers and inductors are critical. There is nothing inherently wrong with the circuits, they just lack all the information you need to be able to construct them. This is about how these things work, not how to build them.
Power factor is not well understood by most electronics enthusiasts, and this is quite understandable because there is little call for it in general electronics circuits. There are aspects of power factor that aren't even understood by many engineers, who should know better. When non-sinusoidal current waveforms are created, even many engineers will do a double-take, because they may not be used to dealing with electronic loads. I shall cover both cases here, and also intend to show both passive and active power factor correction techniques. While passive PFC (power factor correction) has the appeal of simplicity, it actually works out to be more expensive because of the large inductor needed. Active PFC appears complex (and it really is if you have to design it), but once designed uses relatively cheap components.
The simplest case is where a load is inductive. This applies to many electrical machines, including motors, transformers and (of course) fluorescent lighting ballasts (magnetic types). When a motor or transformer is fully loaded, it appears as a resistive load, and has an excellent PF. At light loadings, the same part appears inductive, and this causes the current to lag behind the voltage. Where the load operates in this mode for the majority of its working life, it is necessary to apply correction to return the PF to as close to unity as possible.
The power factor of a resistive load is always unity - it is perfect. Every volt and every amp is used to generate heat. Common examples are electric heaters, toasters, kettles and incandescent light bulbs. Not all loads are resistive though so let's look at a typical example (but simplified for ease of description and understanding).
An electric machine normally runs at half load, but might need the full power at start-up or to be able to handle transient loads. This could be a motor or a transformer - being two of the most common electric machines in use (a fluorescent lamp with magnetic ballast is slightly more complex). In each case, the inductive and resistive components of the load will be equal (for half power), and the voltage, current and power waveforms look like this ...

Figure 7 - Electric Machine at Half Power
As expected, when the resistive and inductive components are equal, there is a 45° phase shift, with the current lagging behind the voltage (lagging power factor). The applied voltage is 240V, the resistive portion of the load is 120 Ohms, inductive reactance is also 120 Ohms, and the power is 240W. We should draw 1A from the mains (240V x 1A = 240W), but instead draw 1.414A. The additional current has to be supplied, but is completely wasted. Well, this isn't strictly true - it is returned to the supply grid. If many loads do the same thing though, then it is simply dissipated as heat in the transformers, transmission lines and power station alternators. Very few real loads are capacitive, so a capacitor is added to the circuit.
With a 45° phase shift, the power factor is 0.707, and we are drawing 1.42A from the mains instead of 1A. To restore the current so that it is in phase with the voltage, we need to add a capacitor to the circuit. A capacitor is effectively the opposite of an inductor, and (by itself) will create a leading PF - the current will occur before the voltage. By adding a capacitor of the right value to the circuit, the power factor can be restored to unity, resulting in a significant reduction in the current drawn from the mains. For this example, 13uF is almost perfect, but even 10uF will reduce the lagging phase shift to 14.2°, and this raises the power factor to 0.96 - generally considered to be as close to perfect as ever needed.
The whole process is somewhat counter-intuitive. That a load may draw more current then it should is easy enough to understand, but that drawing more current again through a capacitor will reduce the mains current does not appear to make any sense. It's all to do with the relative phase of the two currents, and it really does work. Our power system would be in dire straights if it didn't.
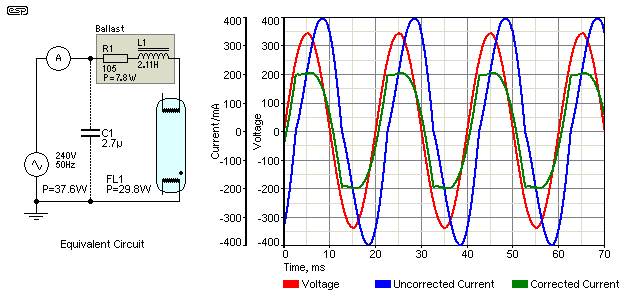
Figure 8 - Fluorescent Light During Normal Operation
The somewhat simplified diagram above shows the voltage and current waveforms of a fluorescent lamp. The simplification is because simulators don't include non-linear negative resistance loads, but the basic principle (and the resulting waveforms) are not materially affected. As you can see, the current waveform is slightly distorted, and this affects the waveform after compensation is applied. In effect, the harmonics generated by the distortion are shifted in phase, so the final current waveform looks like a clipped sinewave. Power factor is very good after compensation though, at 0.98 - an excellent result.
Uncompensated, the current drawn is 276.5mA (giving a power factor of 0.57), and after compensation, this drops to 159.5mA. Power in the load (the lamp itself) is 29.8W, and the resistive component of the ballast (R1) dissipates 7.8W - this is wasted as heat. All wasted heat reduces overall efficiency, but this is unavoidable because real components have real losses.
Things get a lot worse when a non-linear (electronic) load is used. Figure 9 shows the equivalent circuit and waveforms - current is drawn only at the peak of the applied voltage. While this current is in phase with the voltage, power factor is dreadful because the current waveform is nothing like a sinewave. The abrupt current peaks have a comparatively high RMS value, but the power supplied and delivered to the load is a great deal less.
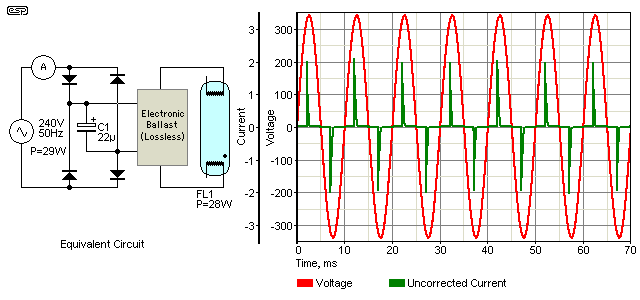
Figure 9 - Electronic Load Power Waveforms
The corrected current is not shown, for the simple reason that significant additional components are needed to correct the waveform. Unlike the case where the load current is (or is close to) a sinewave, just adding a capacitor will not achieve anything useful. The current spikes are such that they can only be removed by using a filter, designed to pass the mains frequency only. As shown, the current is 296mA, but as is evident, the peak value is almost 2A. The load dissipates 28W, but the 'apparent power' (VA) is 71.4VA. This gives a power factor of 0.39 - very poor indeed. In case you wondered where the 1W difference between the source and load disappeared to, that is lost in the diodes.
By adding a filter (passive PFC) consisting of an inductor and a couple of capacitors this can be improved, but the requirement for a relatively large inductance adds considerable weight and cost. One Henry is about as small as you can use for the load's power rating, and although a larger value will work better, it will also be larger again - as well as having higher losses. For these reasons, passive PFC is not commonly used with switchmode power supplies.
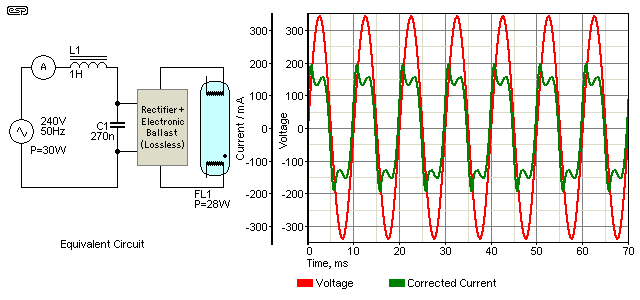
Figure 10 - Passive Power Factor Correction
By adding an inductor and capacitor as shown, the power factor is improved quite dramatically. The current waveform is still not very good, but is far better than the circuit with no correction at all. The RMS current is reduced from 296mA to 136mA, giving 32.6VA. Load power is 29W, so the power factor is now 0.88 which is far more respectable. As in Figure 9, the electronics are considered essentially lossless. Needless to say this is not the case, but the discussion is PFC rather than circuit losses.
The inductor (L1) is a relatively large component, and because of this will be comparatively expensive. In order to reduce cost and weight, an electronic PFC circuit is a better proposition, and it will also be more efficient. Lower power losses mean less wasted heat and cooler electronics.
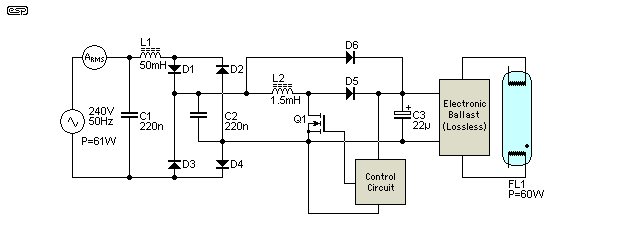
Figure 11 - Active Power Factor Correction Circuit
The scheme shown here is almost identical to that in Figure 5, but is simplified so it can be understood more easily. The incoming mains passes through the EMI filter, consisting of C1 and L1. It then goes to a bridge rectifier, but instead of a large electrolytic cap, a 220nF (C2) capacitor is all that's needed. The output is pulsating DC, and varies from almost zero to the full peak voltage (340V for a 240V RMS supply). This then passes to a very clever switchmode boost converter - L2, Q1 and D5. This boosts whatever instantaneous voltage is present at its input to the peak voltage - in this case the simulated converter stabilised at 446V (somewhat higher than normally used).
The on and off times are carefully controlled to maintain a current that is proportional to the incoming AC waveform, so the duty cycle (on-off ratio) constantly varies to maintain the correct boosted voltage and proportional current. D6 is included to allow the main filter cap (C3) to charge quickly from the mains, and also provides a 'top-up' charge to the cap. This allows some simplification in the control circuit.
The output voltage of the boost converter is (usually) regulated, but the regulation doesn't have to be wonderful, which again simplifies the circuit to an extent. In the circuit shown in Figure 5, you see that the boost converter's inductor (1.58mH) has a secondary winding. This is used to tell the controller IC when the correct current has been reached. The simplified circuit shown in Figure 11 doesn't use this - the switching period is fixed (the circuit was simulated so I could produce the current waveform shown below). While this simplified version isn't quite as good as the 'real thing', it does work rather well - in the simulator at least.
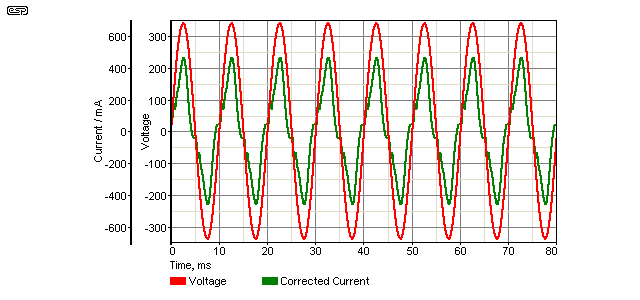
Figure 12 - Active Power Factor Correction Waveforms
As you can see, the current waveform is rather distorted, but the measured performance from the simulator is quite impressive despite its relative simplicity. With 60W in the load (the ballast and fluorescent lamp), actual mains power is 61W (diode losses as before), and with 266mA mains current, it draws 64VA. Power factor is therefore 0.94 - a very satisfactory result indeed. This is significantly better than the passive PFC scheme, and this is to be expected. All analysis that I have seen indicates that an active PFC circuit will outperform a passive circuit, both in terms of overall efficiency and power factor. The inductors are small (electrically and physically), and losses will be much lower than those in any passive PFC circuit.
In case you were wondering, the lamp power is double that of the two previous examples because of the boost converter's higher than desired output voltage. I was most reluctant to spend a lot of time trying to match the power levels, and my simplified version has no regulation. Getting the simulation for the switchmode converter to run happily was a challenge, and simulations take a long time to run because of the high frequency switching.
It is now fairly standard that the waveform distortion is quoted as THD (total harmonic distortion), which in the case of the active PFC circuit is 11.7%. Make of this what you will.
One thing that is fairly critical for proper operation of all mercury arc fluorescent lamps is temperature. There is a relatively narrow band above and below which the arc is diminished, resulting in lower than expected light output. When a tube is cold, there is less mercury vapour available, so the arc cannot reach full strength because there are not enough mercury molecules available to maintain the discharge at the desired level.
When the temperature is too high, the vapour pressure increases, increasing the arc's effective impedance, and again reducing the discharge current. For most compact lamps (and probably most standard fluorescent lamps as well), the tube should be at around 40°C for maximum light output. At 0°C, light output is only 40% - a very dim lamp indeed. Higher temperatures are not as drastic, but a lamp that runs too hot will still be down by a significant amount.

Figure 13 - Light Output vs. Temperature
As the temperature approaches -38.83°C, light output ceases altogether. This is the temperature at which mercury freezes, so there can be no mercury vapour to support the arc and emit UV radiation. In addition, as the temperature decreases, the voltage needed to strike the arc increases, and at 0°C the lamp will need about 40% more voltage to strike, compared to the strike voltage at normal ambient temperatures.
In many parts of the world, 0°C (or less) is a normal ambient temperature for many months of the year, so the lamp will be harder to start and will have low output until the tube heats up a little. In such climates, the tube should be enclosed to protect it from wind that may reduce the temperature and light output significantly.
| Relative Light Output (RLO) [3] | ||
|---|---|---|
| Ambient Temp | Open Fixture | Closed Fixture * |
| -10°C | 25% | 50% |
| 0°C | 50% | 80% |
| 10°C | 80% | 100% |
| 25°C | 100% | 98% |
* Note - a closed fixture provides a +10°C rise over ambient
Like all material on the topic, there are variances in the way the material is presented and different tube types may have substantial variations one from another. The figures are largely in agreement with the above graph, but the small note assumes that the stated temperatures are at thermal equilibrium. This may take some time to stabilise, so initial light output when the lamp is first switched on will be the same for open and closed fixtures. Since the fixture volume with respect to the lamp is not quoted, there will be large variations if the housing is larger or smaller than the (unstated) values used for the table.
 Main Index
Main Index
 Lamps & Energy Index
Lamps & Energy Index