NTC Thermistor Selection

Project 39 has been available for many years (it was published in 1999), and has proven to be reliable and effective. I've had no reports of failures in use, although a small few constructors have made errors when populating the PCB. The recommended current limiter has long been 3 × wirewound resistors in parallel (to get 50Ω for 230V or 33Ω for 120V). Over the years, a few people have asked about or used using NTC thermistors (including me), and although I have tested this option, I've been a bit wary. This was simply because finding good information on their capabilities was so hit-and-miss.

The makers of wirewound resistors almost never publish details of the maximum instantaneous current, and I determined the optimum values by experimentation. NTC thermistors have been a secondary recommendation for some time, but after working through the maths (and run tests), I've decided that thermistors really are a better proposition.

The difficulty has always been the way manufacturers specify the NTC ratings, and (predictably) it's almost never done in a way that is useful. By doing a few simple maths, I've been able to make some specific recommendations, and the reasoning I used is shown below. The suggestions are based on decoding the makers' specifications, along with testing - always the final arbiter.

For reference, a photo of the thermistors I've tested and referred to in this article is shown above. It's not even mildly exciting, but you probably wouldn't expect it to be

. The 20mm NTC is rated for 47 Joules, and the 13mm version is 25 Joules. The significance of this is described below. These seemingly fairly low ratings are far more robust than they may appear at first!

Inrush current can be very challenging, and it doesn't matter if the load is a transformer, a capacitor following a bridge rectifier (as used with SMPS), or a transformer connected to a bridge rectifier with a large filter capacitor. The latter will be assumed for most of the examples shown here, as this is a very common arrangement for DIY power supplies for power amplifiers. The maximum worst-case instantaneous current is normally limited only by the transformer's primary resistance, along with the impedance of the mains wiring (from the local distribution transformer/ substation), the house wiring and the resistance in the power outlet and mains lead.

With 230V mains, the impedance/ resistance at the wall outlet is typically around 1Ω, but it can vary. 120V mains requires larger wire, and for the same loss the resistance will be roughly 0.25Ω. The primary winding resistance of a transformer depends on its VA rating and design voltage, and larger transformers have correspondingly lower winding resistance. The theoretical maximum inrush current for a 500VA transformer with no inrush limiting is somewhere up to 64A with 230V mains.

Table 1 - Typical Toroidal Transformer Specifications
VA	Reg %	R_pΩ - 230V	R_pΩ - 120V	Diameter	Height	Mass (kg)
160	9	10 - 13	2.9 - 3.4	105	42	1.50
225	8	6.9 - 8.1	1.9 - 2.2	112	47	1.90
300	7	4.6 - 5.4	1.3 - 1.5	115	58	2.25
500	6	2.4 - 2.8	0.65 - 0.77	136	60	3.50
625	5	1.6 - 1.9	0.44 - 0.52	142	68	4.30
800	5	1.3 - 1.5	0.35 - 0.41	162	60	5.10
1000	5	1.0 - 1.2	0.28 - 0.33	165	70	6.50

In general, an inrush limiter is not needed for any toroidal transformer of 300VA or less, which may increase to perhaps 400VA for E-I transformers. These always have a higher resistance than toroidal types, and the magnetic circuit is not as 'perfect', so the cause of high inrush current (saturation) is not as pronounced. However, using an inrush limiter with lower powered transformers can still be beneficial, especially if the transformer makes mechanical noise when powered on. You know that you need an inrush limiter if the lights dim momentarily when the transformer is turned on (and no, I'm not messing with you).

For the examples that follow, a toroidal transformer is assumed, and the primary voltage is 230V RMS. A 500VA transformer is a 'good' size, and a high inrush current is assured - especially if the mains is connected at zero voltage (this guarantees maximum inrush current). P39 is a very popular project, and the project article describes two different limiting devices - resistors and NTC (negative temperature coefficient) thermistors.

Resistors require little comment, other than that they must be able to handle the peak current, and this information is not always available (readily or otherwise). All wirewound resistors can handle an instantaneous power of many times their steady-state rating (e.g. 5W for P39). The tricky part has always been to arrive at a sensible compromise, where the resistor survives the peak current/ power without failure. It's quite easy (and I've proven this by experimentation) to cause a rugged-looking wirewound resistor to fail - sometimes spectacularly!

Unfortunately, data are seriously lacking when it comes to the peak instantaneous current that wirewound resistors can handle. Metal film resistors may have this specified, but it's generally lower than desirable (e.g. 5 times the rated current for 5 seconds). This doesn't tell us how much power can be dissipated for 3-5ms ('typical' time for an inrush current event). The 5W, 150Ω resistors I suggest for P39 will dissipate a peak of 770W for ~3ms, and I know that they can handle that quite easily.

The biggest issue with any form of inrush mitigation is power dissipation. Once the first few milliseconds are over it's academic, but in those first few ms, the instantaneous energy is extreme. The thermistors described below are often described as having a maximum capacitive load, which varies depending on the size and resistance of the thermistor. The same criteria apply with fixed resistors - the device must be able to carry the peak current without failure. It needs to be able to do this for many years - essentially for the life of the equipment.

The way this is specified is not necessarily clear, and it's often unhelpful. Some suppliers state a maximum capacitance and a DC supply, others specify an AC supply. Ultimately, equipment is turned on at a random phase, which varies from zero to the peak (5ms for 50Hz, 4.16ms for 60Hz), back to zero. The switching 'event' can occur during a positive or negative half-cycle. The graph below shows the two main possibilities - the peak current will be between the minimum (zero-crossing) and maximum (peak) every time the equipment is powered on.

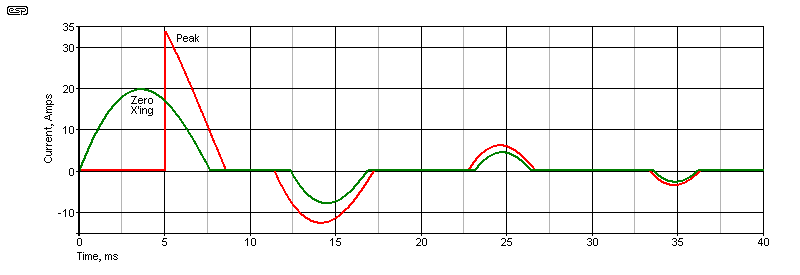
When the mains is turned on at the AC waveform peak, the maximum capacitor current is simply the peak voltage of the AC, divided by the resistance. For nominal 230V mains, this is 325V (170V for 120V mains). The peak is 340V for the graph, meaning that the worst-case maximum current through a 10Ω resistor is 34A, an instantaneous dissipation of 11.56kW (not a misprint!). It's harder to calculate the peak current when switching at zero volts, as it requires calculus to get the answer. However, the simulator tells me that it's just under 20A (19.7A in fact). This reduces the peak dissipation to 3.88kW. The power remains above 1kW for just over 5ms (at 50Hz). Note that peak switching for a transformer load requires little or no inrush mitigation

It doesn't matter whether we use a resistor or a thermistor to limit the current - the peak dissipation isn't changed. To get a lower dissipation, the resistance has to be increased. If we double the resistance, the current is halved and so is the power. My recommendation has always been to use somewhere between 30Ω and 50Ω for inrush limiting, so the worst-case total dissipation becomes 3.8kW, or just under 1.3kW each if three 10Ω resistors/ thermistors are used in series. This may seem highly unrealistic, but it's not - this is reality. The standard value suggested for P39 is 3 × 150Ω resistors in parallel, which means each dissipates a maximum of 770W, but that lasts for less than 5ms.

In all cases, there is some mitigation of the peak current, due to the transformer's winding resistance along with stray resistance. The 'stray' resistance is the combination of the mains impedance (typically around 1Ω for 230V mains or ~250mΩ for 120V), plus resistance in the mains lead, switches and the equipment's internal wiring. For an off-line (mains powered) SMPS, the capacitance should not exceed the value specified in the thermistor datasheet. For the N13SP010 thermistors I've referred to in this article, that means less than 430μF. The specification for maximum capacitance is more-or-less useful for an SMPS with a capacitor filter (the vast majority), but it's not helpful if your load is a transformer.

Unfortunately, while thermistors are specifically designed for inrush current mitigation, the specifications are not easy to decode. Different manufacturers use different ways to describe the peak current, and converting from one method to another is not intuitive. In some cases, the datasheet may specify the peak allowable energy (in Joules), while others give a maximum allowable capacitance charged from a given DC voltage. For those unused to Joules, 1J is 1W/s (i.e. 1W for 1 second).

I'm at a loss to understand why the peak current/ power isn't specified, as that would make selection easy. If you know the peak current, the resistance needed is easily calculated. As an example, I have a bag of N13SP010 (13mm diameter, 10Ω) thermistors, and the datasheet says that with a DC supply of 340V, the maximum allowable capacitance is 430μF. Being 10Ω the peak current is not necessarily 34A as you'd logically imagine - when charging a capacitor (from 240V RMS), the actual current depends on when the power is applied during a half-cycle. If power is applied at the zero-crossing, the peak current is ~19.6A, but if it's powered on at the peak, then the instantaneous current really is 34A. However, the peak current is only above 20A for about 2.2 milliseconds. If we read the peak current as that implied by the application of 340V into a 430μF cap, it is 34A - an instantaneous power of 11.56kW, remaining at over 2kW for 3.8ms. I don't consider this to be sensible, but it doesn't exceed the maximum rating.

Somewhat confusingly, in some cases you'll see a specification for P_Max. This is not the maximum instantaneous power, but refers to the maximum power dissipated when the NTC is left in circuit and the equipment is operational. The maximum operating temperature is typically around 150°C. Operating below the maximum means there will be 'residual' resistance in-circuit, and it will cycle depending on load. IMO a bypass mechanism should be considered mandatory, but it's almost never suggested (no, I don't know why either!).

So (at least in theory) the energy is determined by 340V and 430μF, or 24.8J. The problem is that this is still not very useful! It's alright for a capacitive load, but not for a transformer. Sometimes (but nowhere near often enough) the datasheet will specify the maximum energy that can be dissipated, again in Joules. As a general rule (but it's not especially accurate), you can take the rating in Joules, and multiply it by the time period of interest. For this exercise, we have to make some assumptions. A half-cycle at 50Hz is 10ms (8.33ms for 60Hz), but around 5ms is not unreasonable for a transformer and filter bank.

The energy calculation works in either direction (i.e. charge or discharge). When powered from the mains, we have a theoretical advantage that the mains waveform is not instantaneous, and that is helpful with large transformers. If the mains is applied at the voltage peak (325V for 230V RMS, 340V for 240V RMS and 170V for 120V RMS), that is optimum for a transformer, and inrush current is already minimised. This may sound counter-intuitive, but it is the case, as explained in detail in the Transformers articles. The worst case is when power is applied at the zero-crossing, resulting in the maximum possible saturation, with the current limited only by the winding resistance (along with 'stray' resistances due to switching, wiring, etc.).

To determine the maximum worst-case dissipation for a known (or estimated) time period, use the following formula ...

From that, you can work out the peak current if you really want to. For example, if you divide 5kW by 340V, the peak current is 14.7A ( I = W / V ). This is best used as a rough guideline, and should not be taken as gospel. Ideally, you want to keep the instantaneous current (and power) to the minimum possible. Using the peak value as determined next must be considered the absolute maximum, a value that should never be exceeded.

Using the NTC datasheets to calculate Joules from a capacitance, we can determine that the peak current is equal to the peak voltage divided by the resistance. The time constant (R × C) of a 10Ω NTC and a 430μF cap is 4.3ms. The peak power is 11.5kW, falling to 1.65kW after one time-constant. This sounds pretty scary (which is fair because it is), but the makers claim that this is acceptable - albeit the maximum allowable.

If the thermistor is rated for 25J, we should de-rate it by at least 10-20%. Operating an NTC thermistor beyond its claimed rating is not advised! Staying below the stated maximum means that destruction is unlikely. So, if we say ~20J is 'reasonable', that's 20W for one second, or 10kW for 2ms (20J / 2ms), which is fairly easy to achieve. This may look like a scary number, but there is little risk that the NTC will fail, even with that much power. However, the makers consistently neglect to tell us the maximum instantaneous current, so we don't have a firm answer yet.

I would not be happy dissipating more than 10kW for 2ms - that's an instantaneous current of just under 30A. If we use three of these thermistors in series (30Ω for the example used), the worst-case instantaneous current is 11A. That's still a lot of power (~1.25kW each), but it's also assuming that there is no other resistance in the circuit.

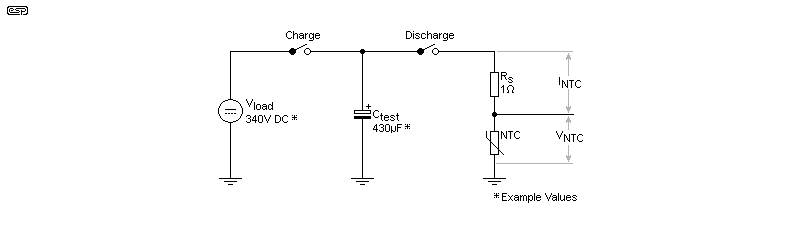
When a capacitance is quoted, the test circuit shown above is assumed. The capacitor is charged to the peak of the mains voltage (e.g. 340V), then discharged through a series limiting resistor into the thermistor. The voltage across the thermistor is measured, along with the current through it. In most cases, the very high initial current is sufficient to cause the resistance to fall (taking around 600μs). There's an application note published by TDK (who make Epcos NTCs) that even shows a graph of current vs. voltage, but as seems typical in these documents, they fail to state which NTC the graph refers to. Whatever it was, the initial peak power was determined to be about 25.5kW (by me - no-one thought to include it). Unfortunately, this is common - the stuff you really need to know is routinely omitted.

Most app. notes and other materials assume a capacitive load, and if an inductive load is even mentioned, it's generally for a motor. Transformers are ignored, even though this is a very common requirement. Also, be aware that some datasheets assume an AC waveform. In theory, the worst-case peak power is the same, but no-one will tell you if they use zero-crossing or peak waveform switching. When it comes to transformer loads, I've done a lot of work on this over the years, and most of it is published on the ESP site. In particular, I suggest that you read Inrush Current Mitigation. The article has real-life current waveform captures and a lot of other info that you'll hopefully find useful.

Transformers are a 'special' case, and they don't behave in the way many people expect. It's quite obvious that powering a capacitive load at the zero-crossing is far less stressful, but it's the worst possible option for a transformer. The captures below show this quite clearly. This is a graph taken from the Inrush Current Mitigation article, hence the transformer is different from the 500VA toroidal described in this article. Regardless, the trend is easily seen, with peak switching reducing the peak current by a factor of nearly five times. It's more pronounced with toroidal transformers!

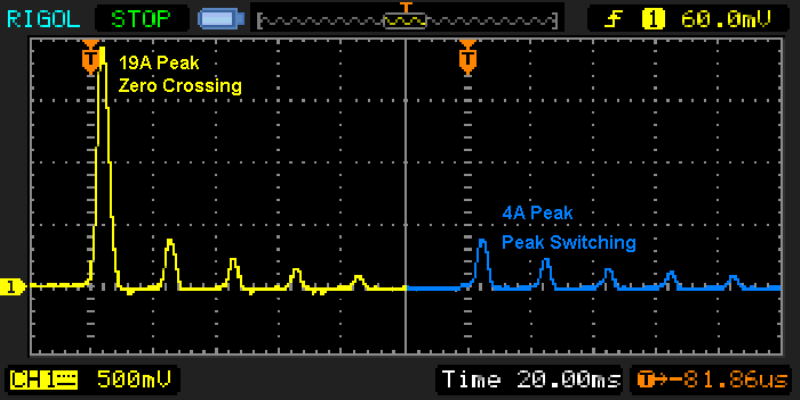
Figure 4 is two captures combined into one, and shows the inrush current waveform captured when power is applied at both the mains zero crossing point and at the peak. The transformer is a single phase, 200VA E-I type, with a primary resistance of 10.5Ω. Absolute worst case current is simply the peak value of the mains voltage (325V or 170V), divided by the circuit resistance. This includes the transformer winding, cables, switch resistance, and the effective resistance of the mains feed. The latter is usually less than 1Ω, and allowing an extra Ohm for other wiring, this transformer could conceivably draw a peak of about 28A. My inrush tester (see Inrush Current Testing Unit) also has some residual resistance, primarily due to the TRIAC that's used for switching. Although it's bypassed with a relay, there is a time delay before the relay contacts close and this reduces the measured inrush current slightly. Peak switching quite obviously reduces the inrush current dramatically, from a measured 19A down to 4A.

Note that the current peaks are unidirectional, and at the mains frequency. The negative half-cycles don't do anything, because the core is saturated in one direction. This unidirectional current introduces a DC 'transient' into the mains circuit, and that can cause other connected transformers to saturate too - even though they are otherwise operating normally. This is known as 'sympathetic saturation' or 'sympathetic inrush' (aka 'sympathetic inrush phenomenon'). So, you owe it to the other transformers in your system to be kind.

For a 500VA toroidal transformer, expect the primary resistance to be 2.4 to 2.8Ω, plus 1-2Ω for the mains circuit. We can reasonably expect that the maximum current that can be drawn at power-on using 3 × 10Ω thermistors won't exceed 10A - enough to cause the transformer to complain a little as it saturates, but not so much that the thermistors can't handle it or for the transformer to make noise. We still don't know for certain if the powdered metal oxides used for NTC thermistors can handle the peak power, but if we can keep the peak current (and therefore power) down to something sensible (i.e. well within the rating in Joules), they should last for a very long time.

The numbering system used by most makers is unsurprisingly inconsistent. If we take the N13SP010 as an example, the 'N' means NTC, '13' is the diameter (in mm), 'SP' is surge protection, and '010' is the resistance (10Ω). From that, you can easily work out that a N20SP005 (for example) is 20mm diameter, rated for surge protection, and has a resistance of 5Ω.

Predictably, there are as many numbering schemes as there are manufacturers, but the majority do make (at least some) sense. Bournes are a well known supplier of electronics products, they have (for example) the BN-LG13Y series. 'BN' is their manufacturer code, 'LG' means they are inrush limiting (no, I don't see how that translates either), '13Y' means 13mm with kinked leads, and the 3-digit resistance code follows (e.g. 8R0 for 8Ω or 100 for 10Ω). Anatherm uses a code of SL12 10006 for the same resistance and diameter. TDK uses a code of B57211P0100M3 for the same thermistor. I'm not even going to try to decode that!

For power transformers, anything less than a 20J rating is almost certainly inadequate, and the smallest NTC I'd recommend is 13mm, 20J or more. The energy rating depends on the resistance, but if you stay within the range of 20-30Ω for 2-3 NTCs in series, most will be suitable. Based on a Yageo datasheet, even their 10Ω, 10mm NTC has a rated capacity of 19J, but the extra safety margin of a 13mm NTC is worthwhile. If you use a small NTC, use three in series (30Ω), but that can be reduced to 20Ω (two in series) with 15mm diameter or more. For example, an N20SP010 will have an energy rating of over 45J, allowing an instantaneous dissipation of over 9kW.

NTCs should never be used in parallel. Their resistance tolerance is fairly wide - a spec of ±20% is not uncommon. I measured a few of the N13SP010 thermistors I have, and the lowest read 11.6Ω, and the highest 13.3Ω. If operated in parallel, the lowest resistance will draw the most current, and it will heat faster, causing it to draw more current. The remaining NTCs may do almost nothing at all, so a series connection is an absolute requirement.

One thing that we should never do is leave the thermistor(s) in circuit. This is often done with SMPS, but it means that if power is interrupted, the thermistor won't return to ambient temperature for some 10s of seconds (or up to a few minutes), depending on its thermal mass. A bypass mechanism is essential, otherwise the thermistor will be constantly cycling as the load current varies. It also means that the thermistor runs hot - up to 150°C at rated steady-state current!

This is why P39 was developed in the first place. It's designed to short out the resistors/ thermistors after about 100ms (5 cycles at 50Hz), so they return to ambient temperature and aren't continually stressed by thermal cycling. Some manufacturers publish 'white papers' or selection guides, but I have found errors and inconsistencies in such literature, so it can be hard to recommend any. Even datasheets aren't usually helpful - they provide multiple graphs of resistance vs. temperature, maximum continuous power and either a rating in Joules or a maximum capacitance for a couple of voltages, but I don't think I've seen even one that specifically states the peak current vs. duration (e.g. 10A for 10ms).

The datasheets nearly all have multiple diagrams showing lead configurations, packaging options and the aforementioned (fairly useless) graphs, but the one piece of information that you really need is missing. It's no wonder that people have difficulties selecting the right thermistor for the job! Hopefully, this guide will help. It's not perfect and there are no guarantees, but I've tested a 30Ω series string (3 × 13mm NTCs) with a 1kVA transformer using 10,000μF filter caps, and I know that this power supply will almost always either blow the fuse or trip my workbench circuit breaker if just powered on 'normally'.

The photo shows a P39 board fully populated, and fitted with three N13SP010 thermistors. This is not the same photo as that shown in the project article, as it's the latest revision of the PCB. There's no difference in the circuit, but the latest version just means that I don't have to use a guillotine to separate the sub-board (the vertical PCB with the thermistors). If you have the earlier version, don't fret, as it's functionally identical. The one in the photo is configured to use an external 12V power supply, but I installed the bridge rectifier anyway.

With the 3 × 10Ω series string of 13mm NTCs, in circuit for 100ms (using P39), the supply can be powered on directly from the mains. The peak current I saw during tests was 11A - pretty much exactly as calculated. After 5 or 6 power cycles, the thermistors were slightly warm - nowhere near hot enough for their resistance to be reduced by very much. The 'typical' operating temperature of NTCs is around 150°C when operated at the maximum steady-state load current. That is seriously hot, and is an extraordinarily non-sensible idea, especially if it's anywhere near semiconductors or electrolytic capacitors.

By bypassing the thermistors after they have done their job (preventing high inrush current) they should always be shorted out with a relay. In theory you can use an SSR (solid state relay), but a standard electromechanical relay (aka EMR) is very hard to beat. They are fairly cheap, very rugged, and have excellent isolation between hazardous voltages (the mains) and the remainder of your circuitry. An SSR will cost more (sometimes much more), and provides no real benefits, other than a lower drive current. The two relays (one for power, the other to bypass the thermistors) will draw about 44mA each, which is negligible compared to the power dissipated by the power amplifiers. The ones I recommend for P39 are extremely rugged, and I've never had one fail (I've used a lot of relays over the years!).

I tested the P39 pictured above with a 1.5kVA transformer that was so vicious at turn-on (zero-crossing) that it blew up my inrush tester.

This was unexpected, as it's tested some pretty savage loads over the years. This particular transformer has a primary resistance of less than 1Ω, and the calculated peak current is over 100A. Even when powered on at the waveform peak (best possible case), the peak current was over 12A. Multiple tests with the P39 gave a maximum peak of 15A, only achieved because the thermistors had heated up - a little. The theoretical peak with cold thermistors is ~10A, but even after multiple turn-on tests the thermistors never became more than luke warm.

The idea of this article is to make it (hopefully) a bit easier for you to determine the ideal thermistors for inrush current mitigation. As it transpires, it's fairly easy to use a compromise value that will work with any transformer/ filter cap combination. Three common 10Ω 13mm NTC thermistors (in series) can be used with almost any transformer, but you can also use two 10Ω 20-25mm types if you can get them cheaply. 230V is always more challenging than 120V, because power is increased by the square of voltage, but something that works with 230V will also work with 120V with no changes. You can use two NTCs rather than three if you like, but they are fairly cheap - around AU$1.50 each.

The advantage of NTCs vs. wirewound resistors is that we have at least some idea of the maximum allowable dissipation, even if it takes some maths to get there. Wirewound resistor datasheets rarely specify the peak (instantaneous) power dissipation, so it can only be determined by workshop testing (and destruction), as I did for P39 when it was first designed back in 1999. To date, I have never heard from anyone who has experienced resistor failure, and I know that the suggested values work because of extensive testing at the time.

However reliable the resistors may be, it's probable that NTCs are still a better choice. When the relay operates, the resistors/ NTCs are shorted out, and if there's a serious fault the fuse will blow. This reduces the chance of a catastrophic failure (e.g. a 'meltdown') from causing an electrical hazard. In some failure scenarios, thermistors may run very hot, but they are designed to do so. The fuse will fail before any serious damage is done, but expect both resistors and NTCs to fail as well. I've seen NTCs explode (not with P39) when subjected to a shorted load, and some people like to enclose the thermistor(s) in heatshrink tubing. However, it's not designed to handle temperatures of 150°C or more, and it's likely to prove useless.

The only external references used were manufacturer datasheets. Many of the various 'selection guides' that I've seen are not useful. Some are drivel - completely useless and riddled with errors!

However, it's worthwhile looking at the Project 39 article, which explains the various functions needed by a workable inrush limiter. Also of interest is the Inrush Testing Unit (aka Project 225), along with Inrush Current Mitigation. These articles are probably the most complete that you'll find outside of academic papers on the topic (many of which are purely theoretical).

NTC Thermistor Selection For Inrush Limiting