

|
| Elliott Sound Products | Microphones II |
 Main Index
Main Index
 Articles Index
Articles Index
Before anything else is discussed, it's very important to understand that all sound measurements ultimately depend on the location of the microphone in relation to the sound source. Nearby surfaces cause reflections, some surfaces are (at least partially) absorptive, and the relative distances have to be considered in respect of the wavelength(s) of the sound being measured. Moving the mic (or meter) position by just a few metres can change the measured result by anything from a fraction of a dB up to 10dB or more. The relative sizes of any boundaries also have an effect, depending on whether they are larger or smaller than a wavelength at any given frequency.
Anyone who has tried to measure the response of a loudspeaker will have seen serious anomalies in the region of 150-300Hz, where the distances between the mic, floor and ceiling cause reflections that show up as (usually) a huge response dip, which is accompanied by other peaks and dips at various frequencies where the relative distances are related to wavelength. These errors are not subtle, but as humans listening with our ears, the effect is greatly diminished - often to the point where we don't hear the response variations at all. Microphones are dumb, and they don't have our brain's processing power. This is why sound measurements and reality often don't coincide, unless extreme care is taken when the measurement is made. When measuring noise, A-Weighting only ever manages to make a bad situation worse.
On the basis of the above, it's somewhat surprising that the 'authorities' (whomever they may be) will insist on the use of a carefully calibrated microphone, but don't usually ask for a detailed drawing of the measurement position, including reflection and absorption coefficients and sizes of nearby surfaces. Be that as it may, it's expected that any measurement of SPL will be done using meters of a certain standard, and that they will have been calibrated before use. Needless to say, measurements will almost always be A-Weighted, despite the fact that the use of A-Weighting is almost never appropriate because it throws away everything that is likely to be really annoying.
None of the above is intended to imply that calibration is somehow 'unimportant' though. How the mic performs (with or without attached sound level meter) certainly matters, and both level and frequency response should be within predetermined limits to ensure that readings are as accurate as needed, and are reproducible. If two people take a reading from the same location using different meters, it is expected that they should get the same answer (with a small allowance of perhaps 1dB or so). The world of acoustics would be in a very sorry state if it weren't for the standards that exist to ensure that results are as accurate as can reasonably be expected. Other issues that may arise are then the responsibility of the person taking the measurement, not the equipment.
There are many different types of microphone, but in the world of measurement there are only two that comprise the overwhelming majority. The first, and the one with the longest history, is the externally polarised capacitor ('condenser') mic, which dates back to 1916. A DC voltage of up to 200V is used to polarise the capacitance between the diaphragm and back plate. When the diaphragm moves as it's exposed to air pressure variations (aka sound), the capacitance changes and an AC voltage is generated that's an electrical equivalent of the sound.
The other popular mic is the 'pre-polarised' capacitor microphone, more commonly known as an electret. Instead of an external DC supply, a charge is permanently 'embedded' into an insulating material, and this is generally used as the back plate (often referred to as a 'back-electret'). Early electret mics used the diaphragm as the electret material, but this is rarely seen any more. Electret mics come in two versions as well, with consumer versions having an in-built FET impedance converter. Professional electret mics use an external impedance converter as part of the powered preamp, and the mic capsule is screwed onto the preamp.
The frequency response of a measurement microphone is not as simple as it may seem. The response is determined by the sound field for which the microphone is designed. There are three different ways that a measurement microphone may be calibrated, being free field, diffuse field, and pressure. A free field is defined as a space with no reflections (an anechoic chamber), with the source being measured at 0° incidence to the microphone (i.e. directly facing the diaphragm). A diffuse field is a reverberant acoustic field in which sound has an equal probability of coming from any direction. The diffuse field response for a random incidence microphone is the average of the response of the microphone's response at varying angles of incidence. A pressure microphone is assumed to be flush mounted with the boundary of the acoustic chamber, and unlike the other two calibrations is not itself a part of the sound field.
All microphones can be used in all sound fields, but each sound field registers a different response in the microphone. This is due to the geometry of the mic itself being a part of the sound field. In the case of pressure response, it is assumed that the mic is not 'immersed' in the sound field, so its geometry is not a factor. The different effects don't have any significant influence at frequencies where the size of the microphone's diaphragm is small compared to wavelength, but it becomes important at high frequencies (typically above 10kHz where the wavelength is less than 35mm). This is a topic that could easily occupy an entire article itself, but this is not that article.
However, the smaller the microphone itself (and its housing) the better it will function at high frequencies. While 25mm (1") diameter measurement mics used to be the standard, most are now 12.7mm (1/2"), and some are available down to 6.35mm (1/4"). Because the smaller diaphragms have dimensions that are significantly smaller than the wavelength of sound (even at 20kHz), there is less disturbance of the sound field and HF performance is improved. When protective grilles are added, these also cause some interference, but of course they are necessary to prevent damage to the delicate diaphragm. We have to live with some limitations, and doubly so in a field measurement application where the mic has to be used in all kinds of environments. Not all of these are friendly!
When taking any readings of SPL (sound pressure level), it's important to know that your meter and its microphone are accurate. Professional meters are either Class-1 (the best and most expensive) or Class-2. The latter are more affordable, but those you buy from your local electronics shop are usually neither - they don't have the required accuracy to be classified. They'll certainly give you an indication of the approximate level, but it could be out by a couple of dB and you wouldn't know. In many cases it doesn't matter, because as discussed (briefly) above, the location of the mic can change the response dramatically. There are also apps for smartphones, but most don't have any provision for calibration (even with an external microphone), so are best considered as toys.
While you can get any microphone or sound level meter (SLM) professionally calibrated, there's no guarantee that it will remain in calibration for any length of time, and in some cases the mic sensitivity may be temperature dependent, or affected by humidity. Rough handling can also affect the mic, and very high quality mics are likely to be rather delicate.
It's important to understand that this article is a generalised view of microphone calibration, and is not intended to describe the different processes used in great detail. For example, mics can be calibrated using a pressure system or acoustic coupler (as described here) or 'free field' in an anechoic chamber. There is also calibration by 'reciprocity', where a reference microphone is used to provide an excitation signal (i.e. it acts as a sound source) for the mic under test. In this case, the diaphragms are close coupled, being separated by the smallest possible distance. In some cases, air is replaced by hydrogen as the coupling medium - especially for high frequency calibration. Another method uses an electrostatic field to excite the diaphragm directly (no sound is produced), but this only works with metallised diaphragms as used with capacitor ('condenser') mics (electret or externally polarised).
This article concentrates on the use of a conventional air-filled acoustic coupler driven by a suitable small transducer (typically a miniature speaker), although the use of small pistons is also discussed. These calibrators are usually fixed frequency, although there are some that offer several frequencies.
The standards that apply vary by country, but IEC 61672-1:2013 is recognised in most places. This defines a wide range of performance criteria that the SLM must meet. These criteria are technically complex and detailed and have tolerances for response at various frequencies. In the current IEC standard there are two levels of tolerance, and these are known as Class 1 and Class 2. The following table provides abridged data for the two classes ...
| Frequency | Class 1 (dB) | Class 2 (dB) |
| 1kHz (Reference) | ± 1.1 | ± 1.4 |
| 16Hz | +2.5, -4.5 | +5.5, -∞ |
| 20Hz | ± 2.5 | ± 3.5 |
| 10kHz | +2.6, -3.6 | +5.6, -∞ |
| 16kHz | +3.5, -17 | +6, -∞ |
Depending where the information comes from, you may find different results. The American National Standards Institute (ANSI) specifies sound level meters as three different Types 0, 1 and 2. These are roughly equivalent to the Classes defined by the IEC (International Electrotechnical Committee), but there are some subtle differences that mean the classifications do not necessarily translate from the US to Europe and other countries including the UK, Australia, New Zealand, and many others that use IEC based standards. Another class exists - Class 0, and these meters are generally considered laboratory grade and are not intended for field work.
Regrettably, most countries mandate the use of an A-Weighting filter (See Project 17 for an example), which was originally intended for use only in quiet locations, but is now inappropriately used for everything. I've been railing against this insane approach for many years, because it completely negates the sound that travels the furthest and causes the most annoyance - bass! Nevertheless (and unfortunately) it exists, and there are great many noise polluters who will fight tooth and nail to ensure it remains. Why? Because it lets them get away with far more low frequency noise than is good for people's health and wellbeing (something they universally deny outright).
There are other weighting filters used, with C-Weighting being common on all meters that are aimed at professionals. Pity that most don't actually use it. C-Weighting allows for some rolloff below 100Hz and above 10kHz, with a typical response that's roughly 6dB down at 20Hz and 10dB down at 20kHz. Z-Weighting is intended to be flat from 20Hz to 20kHz. There are some others as well, but if you want to know more, I suggest a web search.
The response of all meters with A, C and Z-Weighting is the same at 1kHz, and the most common calibration tone is 1kHz (±0.2%, < 1% THD - total harmonic distortion). The level is usually 1Pa (1 Pascal) which equates to 94dB SPL. Some calibrators also offer higher SPLs, with 114dB being fairly common (10Pa). Laboratory calibrators can generally test over the full frequency range and at various levels in addition to the standard 94dB, and are used to calibrate lab grade microphones which are then in turn used to verify that a calibrator is accurate.
This is all very convoluted, and it can be extremely difficult (and expensive) to get a calibrator properly calibrated unless you are willing to pay for a lab to perform the work for you. Early calibrators (in particular from Brüel & Kjær in Denmark), used what is called a 'pistonphone', where the reference SPL is generated from a carefully calibrated pair of pistons driven from a motorised cam. Because the displacement of the pistons and the volume of the measurement chamber are tightly controlled, the reference SPL can be calculated (with a barometric offset - and yes, the barometer is supplied in the kit). Pistonphones generally produce a 250Hz signal because it's not possible to obtain perfectly predictable displacement at higher speeds. Several manufacturers now make pistonphones, but they are expensive (even second hand). Because the frequency is 250Hz instead of 1kHz, a correction has to be applied for meters with A-Weighting (the signal will show an SPL of 85.4dB - 8.6dB lower than at 1kHz, as per IEC 61672-1:2013).
Meters also use two different time weightings - 'F' (formerly known as 'fast', with a 125ms integration time) and 'S' ('slow', 1 second integration time). These are also defined in the appropriate standards, and set the rise-time of a reading. Fast response is needed to see the peak level of transients, while slow response is preferred when the background noise is steady. 'I' weighting (Impulse, 35ms) used to be common, but it's no longer defined in the standards and is not used. It may be available on some old SLMs, but isn't provided on any of the new ones.
It's generally accepted that the measurement should be true RMS, although it's usually difficult to find out for certain is this is the case. Certainly, budget meters will be average reading but 'RMS' calibrated, and this means that the reading will only be accurate when monitoring a sinewave. While this is expected from a calibrator, most real noise sources will present a complex waveform, and the error can be substantial.
There are many other facilities included in professional SLMs, such as long-term average SPL - LEQ, the sound pressure level in dB, equivalent to the total sound energy over a given period of time. It's accepted practice to include the frequency weighting as well, so LAEQ is the long term average, A-Weighted. Others include LAT - the equivalent steady level over a given period of time that contains the same amount of noise energy as the measured fluctuating sound level. Meters may also include band filters (typically octave or 1/3 octave).
You will also see terms such as LA10, the noise level exceeded for 10% of the measurement period, A-weighted and calculated by statistical analysis and/or LA90, the noise level exceeded for 90% of the measurement period, A-weighted and again determined by statistical analysis. This is a complex area, and the meter setting needs to be set appropriately for the measurement conditions.
As noted above, while meter accuracy is obviously important, many people fail to understand that the position selected for the measurement can make a difference of 10dB or more either way, depending on the surroundings. A measurement taken from in front of a large wall (such as the side of a building) can give very different results depending on the distance from the surface and any openings therein. Unless the terrain information and measurement position is provided, the measurement is virtually useless, and the most accurate SLM in the world won't help one bit.
To be useful, a calibrator needs to meet several criteria, with frequency and level being especially important. A small variation of level due to temperature changes might be tolerable, but only if it's less than perhaps 0.2dB over the 'normal' temperature range of between 0°C and 40°C. Likewise, the frequency needs to be stable as well over the same range, and it shouldn't vary by more than ±0.2% (±2Hz). The distortion requirement isn't difficult to achieve, as it only needs to be less than 1%.
There are many 'low cost' calibrators available on-line (around AU$150 or so at the time of writing), but they may not be especially accurate as supplied. I have modified quite a few for clients because the speaker's back enclosure was not sealed properly and the speaker could also move slightly, which caused the output to change when the calibrator was changed from horizontal to vertical (or vice versa). With most, the levels weren't right either, so they required a second trimpot so that the level could be independently adjusted for 114dB and 94dB. Unfortunately, some of these also show some level variance with temperature, so they are not at all useful for field work where wide temperature changes can be common. After modifications, they will probably scrape through in terms of specifications for Class 2, but they won't satisfy the criteria for Class 1 calibrators because the level changes too much.
It's surprisingly difficult to get a sinewave oscillator to be very stable with temperature, largely because of the need for a system for ensuring that the level remains constant. This apparent contradiction is created by the stabilisation system itself. To minimise distortion, the gain must be dynamically varied so that the waveform doesn't clip (distort). If other factors affect the loop gain of the oscillator (such as thermal effects on capacitors or opamps), the stabilisation network will compensate, but the final output can vary by ±0.5dB or more.
Common stabilisation schemes are to use a small lamp (the #327 lamp is commonly suggested - 28V at 40mA), or some form of electronic stabilisation. Electronic methods will use diodes to get a DC feedback signal (to control a JFET for example), so there's already a -2.2mV/°C change (the temperature coefficient of a 'typical' silicon diode) that has to be accounted for. The diode voltage change may not seem like much, but at a voltage of 1V and a temperature range of perhaps ±25°C, the diode alone represents a total error of a little over 0.5dB.
The above doesn't include any other parameters that may change in other components, such as resistors and capacitors. There will also be changes in the bias current of opamps, and their saturation voltage changes with temperature. Making up a sinewave oscillator may not seem like such a big deal - especially when resources like the ESP article on Sinewave Oscillators - Characteristics, Topologies and Examples are available. Unfortunately, getting a stable sinewave is difficult, particularly when it will be subjected to relatively harsh treatment in the field and will have to perform over a much wider range of temperatures and supply voltages than any piece of normal test equipment. A field calibrator also has to run from batteries, and the varying supply voltage as the battery discharges has to be considered.
More than acceptable frequency stability is assured by using a crystal, and then it only requires a digital divider to obtain the 1kHz needed, plus a means of converting the output squarewave into a reasonable sinewave. This means filters, and they can be affected by temperature as well - largely due to the temperature coefficient of the capacitors used. For this reason, it is essential that plastic film (polypropylene (-200ppm/°C) or polyester/ PET (+400ppm/°C)) capacitors are used. Use of high Q ceramic caps (very common in SMD styles) is not acceptable, because they have a very high thermal coefficient as well as a significant voltage coefficient. That means the capacitance varies widely depending on the instantaneous voltage present, so distortion can be high as well as having very poor thermal characteristics.
The electromechanical part (the miniature speaker or other transducer) also needs to have stable performance over the normal temperature range. The thermal coefficient of resistance of copper is +0.00386/°C *, so a (measured) 8 ohm voicecoil at 25°C will be 7.228 ohms at 0°C and 8.772 ohms at 50°C. This is rather large change, and probably came as a surprise. If driven from a constant voltage, the power change is a little over 0.84dB over a 50°C range (±0.42dB referred to 25°C). This effect can be mitigated by feeding the voicecoil from a higher than normal impedance so the resistance change doesn't cause such a significant error. If an 8.2 ohm series resistor is used (for example), the total variation is reduced to well below ±0.01dB. The optimum output impedance value for the driving amplifier is equal to the voicecoil resistance.
* Note that the temperature coefficient of resistance of copper is somewhat variable, depending on the reference used. The figure shown is typical of published values.
Unless compensated, the resistance change can be a significant source of error over the temperature range typically encountered. Other transducers (piezoelectric for example) are even less stable, so should not be used unless they have undergone extensive testing to ensure thermal stability. It's quite obvious that a calibrator using a copper voicecoil in the speaker cannot be expected to give a consistent result over a wide temperature range unless it's fed from the correct impedance.
Even the atmospheric conditions (temperature, humidity and barometric pressure) make a difference to the measured SPL, and it is vitally important to ensure that any mic inserted into the calibrator doesn't change the internal volume. I was able to find the formulae for calculating the change of SPL caused only by the change of volume of the measuring chamber. Unfortunately, the formula used dynes/cm², an old and outdated measure of pressure (the Pascal is now the standard), but this information is extraordinarily difficult to find anywhere. I must confess that I think that finding the formula at all can only be put down to pure luck. I've converted the formula to suit current standards ...
P = γ × Po × ΔV / V PaWhere
γ = (gamma) the ratio of specific heats for the gas in the enclosure. For air at 20°C and at 1 atmosphere, γ = 1.402
Po = atmospheric pressure = 101.325 kPa
ΔV = the change in volume of ...
V = the reference volume
Reference SPL (0dB SPL) is 20µPa - we'll call this Pref
An excellent example is described in the references [ 4 ], where the displacement of a Brüel & Kjær (B&K) pistonphone is explained in detail. The internal volume is 19ml, and the pistons change this by 6.28µl. If you want to see the process used to determine the piston displacement, please see the referenced document, as the displacement calculations are not shown here. Applying the formula shown above shows that the volume change created by the pistons causes the peak SPL to be 127dB, so the RMS value is 3dB less. First, we calculate the pressure variation ...
P = γ × Po × ΔV / V
P = 1.402 × 101.325k × ( 6.28µ / 19m )
P = 46.954 Pa
Calculating the SPL ...
SPL (peak) = 20 × log ( P / Pref )
SPL (peak) = 20 × log ( 46.954 / 20µ )
SPL (peak) = 127.413 dB
SPL (RMS) = 127.413 - 3 = 124.4 dB SPL
Note that the calculated 0.4dB variation is within the specification for a Class 1 instrument (±1.1dB at 1kHz). As should be apparent by now, none of this is trivial, and even seemingly insignificant changes to the reference volume (because a mic goes too far or not far enough into the chamber for example) will affect the accuracy of the calibration. I leave it as an exercise for the reader to calculate the effect of changing the reference volume by ±1ml for example. Naturally, if the chamber is made smaller, the effect is magnified - and vice versa.
However, the chamber's dimensions must remain small compared to the wavelength of the calibration tone, or standing waves may create gross errors. A larger chamber also needs a greater displacement from the transducer - this is all a careful balancing act. The wavelength of a 1kHz tone in air is about 345mm, and ideally all dimensions will be smaller than 1/4 wavelength (86mm). When B&K designed the original pistonphone, the selection of 19ml for the mic chamber was almost certainly the result of some serious calculations and experiment, and it should come as no surprise that many microphone calibrators use a similar volume to this day. There are variations of course, but in general I expect that based on those I've seen, few will be much less than around 10ml. Note too that most calibrators have a small vent in the main (mic) chamber so that the delicate diaphragm isn't damaged by over (or under) pressure as the mic is inserted and removed. The vent has to be small enough to ensure that it doesn't affect the pressure response at the test frequency.
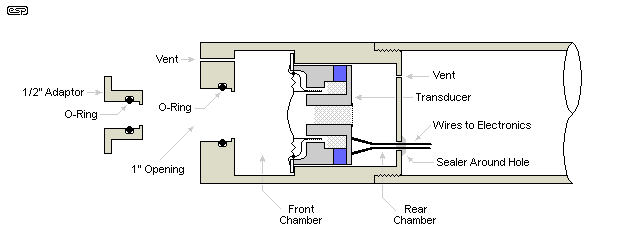
Figure 1 - Calibration Chamber Example
The drawing shows the essential parts of a calibrator's mechanical (hardware) parts. There are many possibilities for the transducer, including dynamic microphone capsules operated in reverse, small speakers, headset/ headphone drivers, etc. Most will be no more than about 40mm diameter. The outer casing can be steel, aluminium, plastic, or a combination of materials. The volume of the two chambers can vary somewhat without affecting performance, because calibration will set the SPL to the correct value. As noted earlier, if the front chamber is too small, the calibration level becomes much more dependent upon very consistent microphone insertion depth. If the mic goes in too far, it reduces the size of the chamber and increases the apparent SPL, and vice versa.
There's a small lip at the end of the hole where the mic is inserted, and the microphone must always be pressed in (gently of course) until it can't go any further. This ensures that the effective chamber size remains the same for each mic you use. It doesn't always work out that way though, because some microphones have a protective grille that distances the diaphragm from the end of the receptacle, and others may penetrate the chamber due to their geometry. If the chamber is large enough, these small variations will only have a minor effect. All calibrators make use of an O-ring to seal the mic and provide a reasonably firm attachment so the mic doesn't move during calibration.
The electronics consist of a battery powered oscillator, with very (hopefully) stable output level and frequency. Some may use more than one level (94dB and 114dB SPL for example), or have several available frequencies. In multi-frequency calibrators, there may be a separate adjustment for each frequency, because the transducer is unlikely to have flat frequency response. It's also necessary to include a battery voltage monitor that either stops the oscillator or turns off the power LED if the voltage is below the allowable minimum.
There are many suppliers of mic calibrators, ranging from top-of-the-line Class 1 units from major manufacturers, all the way down to budget versions available from well known on-line auction sites. However, even 'cheap' calibrators are fairly costly, and even more so if you discover that they don't perform well. Consistency is critical, and if you calibrate the same mic twice in a short period and get two different answers, then which one is right? The first? The second? I suggest that neither can be trusted, so either you aren't inserting the microphone properly each time (so you need to perfect the technique and understand that the insertion distance is usually critical) ... or the calibrator is rubbish.
We can discount the option of reciprocity calibrators (where one mic drives another) because the equipment is very expensive, and the setup is critical and time consuming. Few of us can afford a dedicated anechoic chamber (free field) or even a reverberation chamber (diffuse field), so that leaves us with no choice but to use a pressure calibrator, generally at a single frequency and with a reference level of 1kHz at 94dB SPL. Determining the frequency response is difficult and expensive, so mostly we rely on a calibration certificate from the manufacturer. Some are generic - the graph shown is typical of that type of mic, but more expensive mics will have an individual graph indicating the serial number of the mic and its tested response.
For the vast majority of users, the only sensible option is a pressure calibrator, where the mic is inserted into a close-fitting receptacle (usually sealed with an o-ring). The required frequency and SPL are generated by an electronic oscillator driving a small moving coil transducer, which may be a miniature loudspeaker or even a dynamic microphone capsule used in 'reverse'. Pressure calibrators are the most common, and are the only ones that are suitable for field work because they are easy to use and compact enough to be carried to the site along with the other equipment.
It's rather unfortunate that calibrators are expensive. Even 'cheap' ones are typically at least AU$150 and those from major measurement mic manufacturers have price tags that are quite scary ($400 to $1,000 or more). Having seen the insides of several (from 'cheap' to expensive), I can only assume that the price is based on the comparatively small number that are made and sold, and they don't quite manage to get much economy of scale. A significant part of the cost will always be the microphone adaptor(s) and the transducer + housing. These are difficult for most people to build because they require machining, which generally means that a lathe is necessary.
This doesn't mean that you can't build a calibrator yourself of course, but the required machining makes it that much harder. You also have to calibrate it to a known standard, and that will almost certainly cause most people grief. It's notable that there are almost zero schematics available - most that come up in a search are not calibrators at all.
As noted earlier, the high frequency response is affected by the wavelength of sound, and as the diaphragm size starts to become significant compared to wavelength, the response will change. There is usually nothing you can do to improve matters, so for precision work it's essential to have a microphone calibration chart so corrections can be made as needed. Some high-end measurement microphones use TEDS (Transducer Electronic Data Sheet [ 5 ]), which can provide a compatible measuring instrument with details such as type, operation, and attributes of a transducer. This includes model, serial number, sensitivity, operational limits, and other information that is used to tell the measuring instrument what has been connected.
The minimum frequency for any capacitor microphone is a combination of two main factors. The first is the size of the vent or bleeder. All omnidirectional microphones need a vent so that atmospheric pressure equalises on both sides of the diaphragm. Without any form of vent, a normal increase of atmospheric pressure would push the diaphragm in towards the backplate, and a decrease will pull it outwards. In the extreme, the diaphragm may be damaged, but in all cases the change of distance between the diaphragm and backplate will affect the mic's sensitivity. If atmospheric pressure forces the diaphragm closer to the backplate, the effective capacitance is increased and the sensitivity will be increased. The converse also applies of course. This venting is standard for most directional mics, because the rear vent is relatively large and is part of the process of modifying the directivity.
To circumvent this very real problem, microphones use a tiny vent so that the pressure can equalise, and good low frequency performance requires a very small vent so that pressure equalisation time is large compared to the minimum frequency. For example, if you need to measure below 1Hz, the equalisation time needs to be at least 10 seconds to prevent premature rolloff.
The other major contributor is the impedance presented by the preamplifier, whether it's included in the capsule or external. Consider that the capacitance may only be a few picofarads for a small mic, so the input impedance of the preamp has to be extremely high. For example, a 6mm diameter mic has a diaphragm area of about 28µm². If the diaphragm is spaced 50µm from the backplate, the capacitance can be calculated (as an approximation, because there are several assumptions made) ...
C = 8.85E-12 kA / t ... where C = capacitance (Farads), k = dielectric constant, A = area (m²) and t = dielectric thickness (m)
C = 8.85E-12 × 1.5 × 28µ / 50µ = 7.4pF
The dielectric constant is a guess, because it's partly the diaphragm material (typically Mylar) and partly air, but the calculated capacitance is not far from what I'd expect for a mic that size. The total resistive load on the capacitance can now be determined for the lowest frequency of interest. So, if we want the microphone to be able to measure down to 1Hz (-3dB frequency), the total resistance (including the FET's gate leakage) needed is ...
R = 1 / ( 2π × C × f ) ... where C = capacitance (Farads) and f is the frequency in Hz
R = 1 / ( 2π × 7.4p × 1 ) = 21.5G ohms (yes, that's over 21 gigaohms!)
It goes without saying that if a lower frequency limit is needed, the resistance has to be even higher. I have some electret mics that have been specified for response down to 0.1Hz - and they have been tested and verified at that frequency. That means the 'load' resistor is probably well in excess of 200G ohms - that's not a resistor, it's an insulator. In many cases, the gate of the internal FET is simply connected to the metallisation on the diaphragm with no resistor at all, and the circuit relies on the miniscule surface leakage resistance of the diaphragm and its insulating support to bias the FET.
Of course, many capacitor microphones are larger than the one calculated above, so have more capacitance and can tolerate a lower resistance without suffering loss of sensitivity at low frequencies. However, it's unrealistic to expect more than 40-50pF in any capacitor mic, and even that requires a comparatively large diaphragm area.
Noise in electronic circuits is a fact of life, and can't be eliminated. In most cases, it's necessary to ensure circuit impedances are as low as possible. A 200 ohm resistor generates 257nV over a 20kHz bandwidth and at 25°C - see Noise In Audio Amplifiers for a complete description and some worked examples. Using the above example of a 21G ohm resistor, we need to consider current noise rather than voltage noise. A 21G ohm resistor can be expected to generate a little over 125fA (femto amps) in a circuit, or a voltage noise of 2.64mV with a 20kHz bandwidth. For many mics, this noise voltage could easily be greater than the signal level.
Fortunately, the capacitance of the microphone forms a low pass filter for the noise voltage, effectively shorting it to ground. However, noise at the low frequency end is not attenuated by very much, and it's only reduced by 3dB at the low end corner frequency (1Hz for the example in the previous section). This always means that there is more noise at very low frequencies, and it's made worse by semiconductor shot (1/f) noise. A microphone can be made less noisy by using a higher load resistance, and discarding the extreme low frequency part of the spectrum by tailoring the size of the bleeder vent. The microphone then performs down to the design frequency, but the capacitance is still able to reduce the noise by a useful margin.
A microphone's self-noise (the noise generated by the mic and its associated preamp if it's a capacitor mic) requires a completely soundproof chamber to be measured, and it is almost always expressed in dBA (A-Weighted). For most mics it's expressed as the total noise that exists due to the mic alone, expressed as 'equivalent input noise'. This is the same as using an ideal noiseless microphone in a room with the same noise level. In general, if you need very low self noise you need a large diaphragm capacitor mic, as they are more likely to be capable of getting below around 10dBA, and with comparatively high sensitivity. This is based on 0dBA being the threshold of hearing, a sound pressure of 20µPa. Low impedance dynamic mics are quieter, but are also less sensitive so need more gain.
In some cases, the mic specifications will provide the SNR (S/N ratio or signal to noise ratio). For example, a mic with a sensitivity of -44dB (referred to 1 Pascal) might quote a S/N ratio of 68dB. This means that its noise is 68dB below the reference level, so in this case the self noise is equivalent to 26dB SPL (94dB - 68dB). The use of an A-Weighting filter artificially improves the apparent S/N ratio by filtering out frequencies above 4kHz and below 1kHz. Depending on the frequencies involved, the use of an A-Weighting filter may provide an apparent 'improvement' of 10dB or more, so the figure can be rather misleading, especially if you need to use the mic to measure low frequencies at low levels.
Because they have no electronics, it may be thought that dynamic mics would be quieter than capacitor types, but that's not necessarily true. Ultimately, Brownian motion of air molecules will generate some noise, and as mentioned earlier a 200 ohm resistor has a 20kHz bandwidth noise level of 257nV, and it makes no difference if the resistance is from a metal film resistor or a copper winding. If the mic has a sensitivity of (say) 6mV/Pascal (-44dB), the noise contributed by a 200 ohm voicecoil or transformer winding is -87dB referred to 1 Pascal (unweighted). Equivalent input noise is therefore 7dB SPL (unweighted).
This may sound very good (and it is), but the small signal from a microphone always has to be amplified. A perfect (noiseless) mic preamp will have a wideband noise output of 257µV with a 200 ohm source and 60dB of gain. In reality, there is no such thing as a 'noiseless' preamplifier, and even the quietest will add a couple of dB of noise to that from the mic itself. An 'ideal' mic preamp (zero noise) has an equivalent input noise of -129.6dBu or -131.8dBV (20kHz bandwidth, 200 ohm source). A preamp with an input noise figure of 1nV√Hz has 141nV of input noise at full 20kHz bandwidth, but it's actually higher than that because the noise figure is generally quoted at 1kHz, and it's worse at low frequencies.
We can add the noise voltages together to get total EIN (equivalent input noise), noting that random noise signals cannot simply be added algebraically ...
Total noise = √ ( Noise1² + Noise2² )
Total noise = √ ( 257nV² + 141nV² ) = 293nV (20kHz bandwidth)
If the preamp has a gain of 60dB and we refer the noise to 1V output, that gives us an EIN of -130dBV which is 1.8dB more noise than the ideal case. This figure is rarely found even in the best mic preamps, so if you expect to be able to record a signal at (say) 20dB SPL (200µPascals), you will be competing with the system's background noise. The only option is to use a mic with the highest possible sensitivity, and that will generally mean a large diaphragm capacitor microphone.
It's difficult to get a definitive answer on noise created by Brownian motion of air molecules, but it appears to be in the order of -20 to -24dB SPL, which works to be between 1.25µPa and 2µPa (note that these numbers vary depending on the source, but around -24dB seems to be a popular estimate). It's very doubtful that Brownian motion will ever limit the overall signal to noise ratio of any microphone.
Although nearly all measurements will generally be made using A-Weighting, as regular readers will be aware I consider this to be a fool's errand at best. At worst, it can almost be considered a conspiracy, because it allows noise polluters to escape any form of punishment for generating low frequency noise at often intolerable levels. Even at 31.5Hz (well within our normal hearing range), the SPL is reduced by 40dB and it will barely register. If you listen to sound with 31Hz content, the low frequency content is clearly audible - even at a relatively low SPL. So much for 'international standards'.
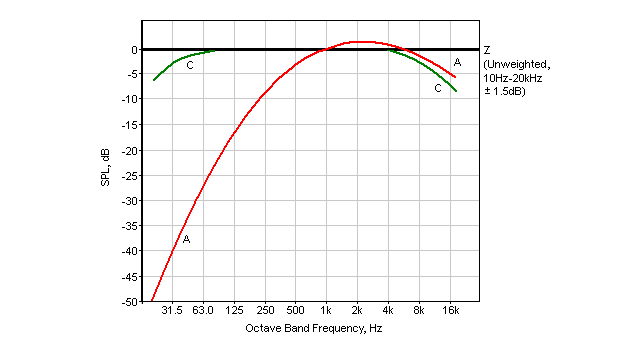
Figure 2 - 'A', 'C' And 'Z' Weighting Curves Compared
The above graph shows the accepted weighting curves, with A-Weighting being by far the most common, and equally the least useful. C-Weighting is better, and Z-Weighting (linear from 10Hz to 20kHz ±1.5dB) is the best of all. Few meters can manage Z-Weighting, because getting flat response to 10Hz is difficult (as noted above in the 'Low Frequency Response' section).
Note that at 1kHz, all weightings provide the same sensitivity, so a calibrator only needs to be able to produce a 1kHz tone. While multi-frequency calibrators exist, they are used primarily in calibration laboratories, and are not generally suited to field usage.
In the interests of science, I conducted a basic test some time ago. I freely admit the test was rudimentary, but it is easily repeated by anyone who cares to do so. I have no doubt that the results will be similar, although will probably be more accurate (I have a basic workshop, not an acoustics laboratory). The test was conducted in my workshop, with the radio playing through my normal system. This includes a subwoofer that can reproduce 30Hz quite easily. Using a sound level meter and a parametric equaliser, I was able to boost the very low bass quite easily. Bass was boosted below about 70Hz, and all other frequencies were unaffected. Average SPL was around 60dBA and 70dBC for these tests. This is roughly the level of normal speech at ~1 metre.
When the sound level meter was set to A-weighting (dBA), it registered no discernible increase in sound level when the low frequency range was boosted, even though the deep bass was clearly audibly increased! Setting the meter to C-weighting (close to flat response), a consistent 6dB increase of SPL was easily measured. Both the meter (when set to C-weighting) and my ears easily detected the low frequency boost, yet the meter indicated no change when set for A-weighting. Bear in mind that most music has little recorded bass below 40Hz and insists on changing as we listen, so a wideband pink noise source was also tested.
The noise level was adjusted until the meter indicated 60dBA, and when the low bass was increased by about 8dB (the range of my equaliser at these frequencies) no increase was shown on the meter. The increased bass was clearly audible, and I verified this by inviting my wife into the workshop to listen to the test. Initially, she thought the deep rumble came from outside (not sure what she thought may have made the noise), but several tests later it was easy to tell whether the equaliser was in or out of circuit. The difference between the normal (flat) condition and deep bass boost was consistently audible. The meter sat stoically showing a level of about 60dBA regardless of whether boost was applied or not. The deep rumble would be extremely annoying if it were present for any length of time.
Without changing any settings (or the meter placement), I switched to C-weighting. The meter then showed the average level as 68dB, and this increased to about 76dB when boost was applied. So the meter now registered that there was about 8dB more low bass energy, and it was clearly audible as before. Acoustic theory (suitable adjusted to give the desired results) tells us that we can't hear these frequencies well, courts and governments believe the theory, everyone insists on using A-weighting (dBA), and they are quite clearly wrong in any case that involves deep bass. I have complained bitterly about the stupidity of measuring all noises (regardless of SPL) in dBA, and this simple test has proved that my complaints are (and always were) justified.
It is remarkable that such a basic test can demonstrate quite clearly that A-weighting is a fundamentally useless way to quantify low frequency annoyance levels, and I urge anyone who is involved in any kind of acoustic testing to run this same test. It is even more remarkable that no-one involved in acoustics seems to have run tests and published their findings, because this is fundamental to our understanding of the perception of low frequency noise.
Note that this test has been performed by others, who have found exactly the same. Low frequency noise is audible, regardless of whether the meter shows it or not !
Measurement microphone calibration is an essential step, but the difficulty will always be actually performing the calibration with a known standard. It's not an issue for organisations who specialise in noise (or sound) measurements, because it's simply part of the cost of doing business. As such, the calibration costs can be amortised across the business, with each client paying a small part of the cost. It's not so easy for hobbyists, because they have to bear the entire cost.
For general work measuring loudspeakers (for example), the absolute accuracy of the mic is immaterial. In 99% of cases it only needs to be able to make comparative tests, with frequency response being far more important than being able to measure SPL within ±0.5dB. As noted at the beginning, huge amplitude errors are common due to mic positioning, and most of these also affect the response. Few of us can afford the space or money for an anechoic chamber, so for the majority of us, speaker listening tests remain the 'gold standard'. Fortunately, most electret mics have remarkably flat response (at least across the frequency ranges needed for most tests/ measurements), so the main unknown remains accuracy of the SPL measured.
In professional acoustics, absolute accuracy is necessary, because without it noise level testing is meaningless. Of course, the use of A-Weighting makes many measurements meaningless anyway, regardless of the accuracy of the microphone and measurement system. Be that as it may, if any measurement is to be made that has to survive legal scrutiny, the accuracy of the system is paramount. For this, calibration is essential, and will ideally be carried out before any measurement is taken. For long-term measurements (typically recording either the actual waveform or the measured results), calibration should be carried out both before and after the measurement, with the calibration results recorded along with the measurement data.
 Main Index
Main Index
 Articles Index
Articles Index