

|
| Elliott Sound Products | LC Oscillators |
LC (inductor/ capacitor) oscillators are almost a thing of the past now, with digital synthesis having taken the lion's share of modern applications. While digital synthesis can cover a wider range and do things that 'simple' LC oscillators cannot, they require a far greater effort to design and build. Like most things analogue, many people might consider LC oscillators to be 'old hat', but they are easy to build and can provide very good performance.
While LC oscillators aren't particularly useful for audio applications, with large enough inductance and capacitance they can be made to work at any (low) frequency you like. High frequencies are the most common place you'll find these circuits, with typical frequencies ranging from a few hundred kilohertz up to around 100MHz or so. Early radio ('wireless' as it was known in the early days) and TV receivers used LC oscillators, as did many other circuits (wireless remote control being a common application).
Crystal oscillators are actually a specialised version of the more traditional LC tuned circuit, except that the tuning is done by mechanical resonance rather than electrical resonance. In this role, the inductance is roughly equivalent to compliance, and the capacitance is (equally roughly) equivalent to mass. Both of these are physically very small, so the frequency is high. The equivalent inductance is generally high (in excess of 1H) and the capacitance very low (less than 1pF), and the Q ('quality factor') is extremely high. Quartz is a piezo-electric material, so when it's flexed it generates a voltage, and conversely when a voltage is applied, the quartz flexes. Metallised electrodes are deposited onto the thin quartz crystal (which is 'cut' to suit the application).
Many audio enthusiasts have (albeit inadvertently) built LC tuned circuits when constructing a graphic equaliser for example. These originally used physical inductors until the development of the gyrator - a simulated inductor (see Active Filters Using Gyrators - Characteristics, and Examples). Gyrators perform as an inductor, by 'reversing' the action of a capacitor. They can be built to simulate a very large inductance (many Henrys), but aren't subject to magnetic fields as would be the case with a physical inductor. However, they are not suited to (and aren't necessary for) radio frequencies.
Passive loudspeaker crossover networks use inductors and capacitors, and they follow the same rules as any other LC circuit. A 12dB/ octave crossover network with an open-circuit (or missing) driver will act as a series tuned circuit at the resonant frequency. It will appear as close to a short-circuit across the amplifier at resonance! This is something that everyone should know, but most constructors are blissfully unaware of the damage it can do.
When an inductor and capacitor are wired in series or parallel, they have a response that's dictated by the value of capacitance and inductance. With parallel resonance, the tank circuit's impedance is (theoretically) infinite, but naturally it can never achieve this due to circuit losses (resistance in particular). In contrast, a series LC network has (again theoretically) zero impedance at resonance. Resistive loss (particularly the resistance of the wire used to make the inductor) is the limiting factor. A series network has one other (very important) characteristic, in that the input voltage is multiplied by the Q ('quality factor') of the circuit. A series LC circuit with a Q of 100 and an input voltage of 1V RMS, will produce a voltage of 100V RMS at the junction between the capacitor and inductor. An example would be a 100µH inductor in series with a 10nF capacitor, having a total series resistance of 0.99Ω.
The resonant frequency is determined by the formula ...
f = 1 / ( 2π × √ L × C ) More commonly shown as ...
f = 1 / ( 2π √ LC )
For the example described above, resonance is 159.155kHz. In radio frequency work, the inductance and capacitance will be a great deal lower. To resonate at 1.59MHz, the inductor could be reduced to 10µH and the capacitance reduced to 1nF (in RF circles this would be often be referred to as 1,000pF). At resonance, the capacitive reactance and inductive reactance are equal, but the signal across each is 180° out of phase. For the 159kHz example, the inductive reactance (XL) is 100Ω as is the capacitive reactance (XC).
XL = 2π × L × f
XC = 1 / ( 2π × L × f )
In each case, f is in Hertz, L is in Henrys and C is in Farads. The values are selected so they are 'sensible' for the impedance of the surrounding circuitry. What constitutes 'sensible' varies widely, and most radio (and TV) circuits will have impedances of several kΩ. This means comparatively large inductance, and equally comparatively small capacitance. In most of the examples that follow, I've aimed for an impedance at resonance of around 100Ω, but some of the other examples will be different as the values can become inconvenient.
The tank circuit is fundamental to LC oscillators, and it's also used for transmitters of all powers. In many cases it uses a tapped inductor (basically an autotransformer), but it can also have a second winding, often to enable the circuit to boost the signal level to ensure reliable oscillation. In other cases, the transformer action is used to match the impedance of the oscillator to an external circuit or transmission line. As interesting as these topics can be, they will only be mentioned in passing, as the possibilities are endless, and this is an article, not a book about RF circuits.

Figure 1.1 - Basic LC Tank Circuits
The basic tank is simply an inductor and a capacitor, along with parasitic resistance. They can be classified as being in series or parallel, depending upon the way the signal is applied. For a series circuit, the signal is in series with the loop, and for parallel circuits the signal is applied from an external source (i.e. outside the loop). The impedance of the source should be high for a parallel circuit, and low for series. Coil (and wiring) resistance is parasitic, and needs to be carefully controlled to obtain high Q. Note that inducing a current into the inductor with a secondary winding is effectively the same as inserting a physical voltage source.
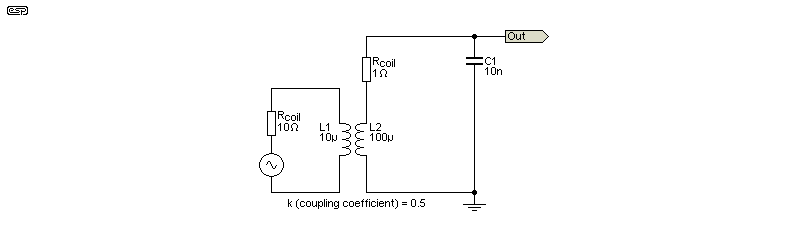
Figure 1.2 - LC Tank Circuit With Inductive Coupling
The drawing poses an important question - is it a series or parallel resonant circuit? While it looks like a series tuned circuit, it's actually parallel. I added a 10Ω resistor to the drive winding, and monitoring the input current shows that the current falls to a minimum at resonance, which tells us that the impedance is at maximum. It's important to understand this, as many oscillators may look like the tuned circuit is a series type, but it almost always behaves like a parallel network. We would understandably expect that the input should be a sinewave, but usually it's not. This is because many oscillators operate in Class-C, so the active device may only conduct for a small fraction of a cycle. So, while the input distortion is very high, the output distortion will be low. A high-Q tuned circuit reduces the distortion more effectively than a low-Q circuit.
The amount of coupling (k) determines how much of the magnetic flux from the drive coil passes through the resonant coil. I used a value of 0.5, which indicates loosely-coupled coils. The actual value depends on how close the coils are to each other, the type of core (ferrite or air) and whether the magnetic circuit is open or closed. A closed magnetic circuit can only be achieved with a high-permeability core that encloses the windings (e.g. a toroidal or E-I type core). The maximum coupling coefficient is unity, meaning that the flux cuts through both coils with no 'leakage'.
There is always phase shift through any frequency-selective circuit. Below resonance, the inductor is dominant, so amplitude increases with increasing frequency. Above resonance, the capacitor is dominant, so amplitude decreases with increasing frequency. At resonance, there is no phase shift with either a series or parallel resonant circuit. Because inductive and capacitive reactances are equal and opposite they cancel, leaving only the coil's winding resistance (plus any other stray resistance).

Figure 1.3 - Basic (Fig. 1.1) LC Tank Circuit Responses
The two examples shown provide a capacitive and inductive reactance of 100Ω at 159kHz. Increasing the feed resistance (Rfeed) for the parallel circuit improves the selectivity (Q) of the tuned circuit. With 1k, the bandwidth (-3dB from the peak) is 17.4kHz and the Q is 9. If Rfeed is increased to 10k, the bandwidth is 3.17kHz, a Q of 50. Figure 1.2 shows the response with the values shown in Fig. 1.1. The main limitation for the Q is the coil's series resistance. The signal source is assumed to have zero impedance for the two tests.
In theory (and assuming no losses), once the tank circuit is triggered into oscillation, it will continue to pass an electric field from the capacitor to the inductor (where energy is stored by way of the magnetic field) and back again indefinitely. The real world does not allow this of course, as losses are ever-present (even if the coil is a super-conductor, as used in MRI systems). Resistance is inevitable in other parts for the circuit, and energy is absorbed by the victim patient. All 'ordinary' resonant circuits are subjected to greater losses (lower Q), and the oscillation dies out quickly.
There's another factor that affects the Q as well - the dielectric losses of the capacitor. Ceramic caps (usually NP0 or G0G, zero temperature coefficient) are common, but in the early days silvered mica was popular. Silvered mica caps are still available, but at a serious cost penalty. Polystyrene (also expensive) is also very good, and polypropylene can be used when high values are required. The so-called 'tuning gang' (a [usually dual] variable capacitor) was used extensively in AM and FM radios until fairly recently. Air is a particularly good dielectric, and has very low losses.
In some cases, the ceramic cap would be chosen to have a particular temperature coefficient to offset the effects of temperature on the tuned circuit. For example, an N750 ceramic cap will show a 2.2% capacitance increase at 0°C, and a decrease of 2.2% at +50°C (25°C is the reference temperature) [ 1 ]. Other common temperature compensation classifications are N450, N330, N220, N150 and N75. The 'N' number specifies PPM/ °C. Somewhat predictably, I won't covering temperature compensation further as it's very specialised.
When it comes to coils (inductors), many RF circuits use Litz wire (multiple thin individually insulated strands woven together) to minimise skin effect. This is a problem at radio frequencies, because the current tends to flow on the outer 'skin' of the conductor, increasing its effective resistance. Many RF coils are made with silver plated wire to give high conductivity for the outer skin, especially for higher power applications. You may have seen RF coaxial cable with a copper-plated single steel inner conductor, and this is done for the same reason. The steel is 'incidental' - it's there to provide support for the copper plating, and of course it adds strength to the cable too.
For very high-power circuits, it used to be common to wind coils with copper tube, with cooling water pumped through the tube. The water was (is) generally de-ionised or distilled to ensure low electrical conductivity. When you're dealing with transmitters delivering hundreds of kilowatts, you need all the help you can get. Needless to say this is outside the scope of this article, and is only mentioned in passing. For completeness, I must include a quote taken from the Radiotron Designer's Handbook ...
With any valve oscillator an exact analysis of the method of operation is very difficult, if not impossible, and it is usual to treat the circuits as being linear (at least for simple design procedure) although they depend on conditions of non-linearity for their operation. This simplification is valuable because the mathematical analysis which can be carried out yields a great deal of useful information concerning the behaviour of the circuits. That the circuit operation is non-linear can be readily appreciated by considering the fact that the amplitude of the oscillations, once started, does not continue to build up indefinitely. The energy gain of the system reaches a certain amplitude and then progressively falls until equilibrium is established. The limits are usually set by the valve-plate current cut-off [which] occurs beyond some value of the negative grid voltage swing, and plate current saturation or grid current damping will limit the amplitude of the grid swing in the positive direction.
The above is not specific to valves, and it applies regardless of the type of amplifying device. These days, full analysis is possible and we have the benefit of very powerful computers, simulators and other tools that didn't exist at the time. However it's often pointless anyway because the tools still cannot take the physical conditions into consideration unless each is specifically accounted for. In particular, stray capacitance, mechanical rigidity and 'incidental' losses via radiation due to the coil's magnetic field interacting with its surroundings remain difficult to model.
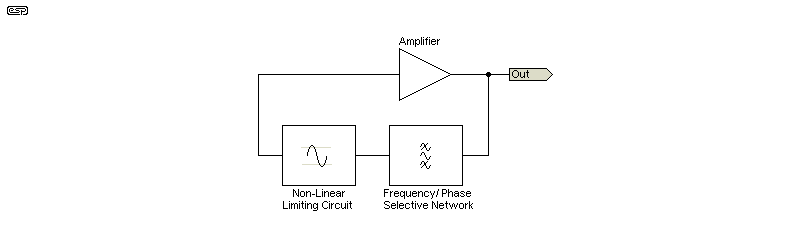
Figure 1.4 - Requirements For An Oscillator
The requirements for all oscillators is the same. It doesn't matter if they are audio or RF, tuned with caps and coils or caps and resistors, they all share the same basics. The first is an amplifier. This must have sufficient gain at the tuned frequency to ensure that oscillation is continuous. If the gain is too low, oscillations will not start, or may be triggered at power-on but die out quickly. The frequency or phase sensitive network is designed to provide zero phase shift at the required frequency of oscillation, so the output of the amplifier is fed back to the input as positive feedback. Finally, there's a non-linear element (explicit or implied) that prevents the oscillation amplitude from increasing forever. In most RF oscillators, this is an 'implied' part of the circuit, so there's no additional parts needed, but the power supply voltage (or available current in some cases) is the limiting factor.
For audio oscillators or RF oscillators requiring high purity sinewave output (low distortion), other methods are used. This will typically take the form of an automatic gain control system, which can be as simple as a thermistor or lamp (at least for audio), or a secondary tuned circuit to remove harmonics generated by the oscillator. In most cases, RF oscillators rely on the tuned circuit to get acceptably low distortion. That's certainly the case with all of the circuits shown below. Distortion (as simulated at least) is less than 3% for all examples. This can be improved by operating the transistor in Class-A (all circuits shown use Class-C, where conduction is less than 180°).
Class-C is very common with RF circuitry, as there is (almost) always a tank circuit that completes the cycle, and it only needs a small 'injection' of energy to maintain oscillation. RF is very different from audio, even though the two may seem to be similar in many ways. The greatest difference is bandwidth, and in most cases this makes audio far more challenging. An AM broadcast receiver has a frequency range of (roughly) 3.2:1, and an audio bandwidth of about 5kHz - a very small fraction of the radio carrier frequency (which is converted to [typically] 455kHz in a superheterodyne AM receiver). The audio bandwidth is a mere 1% of the RF signal. Audio covers the range from (nominally) 20Hz to 20kHz, a ratio of 1,000:1. Note that due to broadcasting requirements, AM radio has an upper frequency limit of about 7kHz, but even that is rarely achieved by most receivers.
Probably the two most common RF oscillators are the Hartley and Colpitts. A variation on the Colpitts oscillator is the Gouriet-Clapp, which provides higher frequency stability. The Hartley circuit gets its name from the inventor, Ralph Hartley, in ca. 1915. The Colpitts oscillator is a variation on the Hartley, in that it uses a capacitive signal 'splitter' instead of a tapped inductor. It was invented in ca. 1918 by Edwin Colpitts. The Gouriet-Clapp is a variation of the Colpitts circuit, and it looks very similar but for the addition of an extra capacitor.
Preceding the circuits mentioned above was the Armstrong oscillator, invented by Edwin Armstrong in 1912. It's a little more complex, and uses two coils often with some adjustment of the mutual coupling between the two. The 'feeder' coil (connected in the plate or collector circuit) is referred to as a 'tickler' coil. Frequency stability is acceptable, but isn't as good as the Hartley, Colpitts or Clapp (in ascending order of stability). The Armstrong oscillator was the basis for two of Armstrong's greatest contributions to radio - continuous-wave transmission using an oscillator to set the frequency, and the superheterodyne (aka superhet) receiver (after some controversy the earliest patent for the invention is now credited to French radio engineer and radio manufacturer Lucien Lévy) [ 2 ]. Prior to that 'regenerative' receivers were common, using positive feedback to increase the available gain and selectivity.
When all of these circuits were devised, the only amplifying device available was the valve (vacuum tube). They can also be made using bipolar transistors (BJTs), junction FETs (JFETs) or MOSFETs. Any device capable of amplification will work, including opamps, although they generally have limited frequency response. All oscillators can be driven with common emitter, common collector or common base transistor topologies, or the equivalent for JFETs, MOSFETs or valves. Most of the circuits shown use the common emitter connection, although common collector (emitter follower) connections are shown for Hartley and Colpitts circuits.
The three most common circuits are shown in the next section. These are all common-emitter designs, and each is tuned for 159kHz. In some cases there will be minor frequency deviations caused by coupling capacitors (in particular the cap to the base of the transistor), but these are not considered in the circuits shown. All circuits use the same bias and emitter resistances. Most of these oscillators operate in Class-C (much less than 180° conduction time), and signal purity is provided by the tank circuit. For optimum performance, this requires the highest Q possible.
Strictly speaking, the capacitance is a combination of the actual capacitance used, along with inevitable stray capacitance. This may include the collector (or drain/ plate) capacitance, along with any capacitance between the wiring and chassis. There is also inter-turn capacitance in the coil itself. It's important to ensure mechanical rigidity, which in the early days often meant using single-core wiring, suspended between circuit nodes. This isn't an issue with a PCB, but at very high frequencies the losses inherent in fibreglass can play havoc. Ceramic or other low-loss materials are necessary when the frequency is greater than 1GHz, and at lower frequencies when significant power is involved.
In the examples shown here, the coil is indicated as being air-cored. However, this would be rather large for 100µH, and it would almost certainly use a ferrite core to keep the size down. The choice of ferrite composition is highly dependent on the expected frequency, and a core intended for use with lower frequencies (including audio) would show high losses with RF. A coil calculator for air cored coils can be found here: Single Layer Air Core Inductor Calculator. A 25mm diameter coil with 100µH inductance will be 5.1mm long using 0.1mm enamelled wire, with 51.6 turns. This would require about 4 metres of wire.
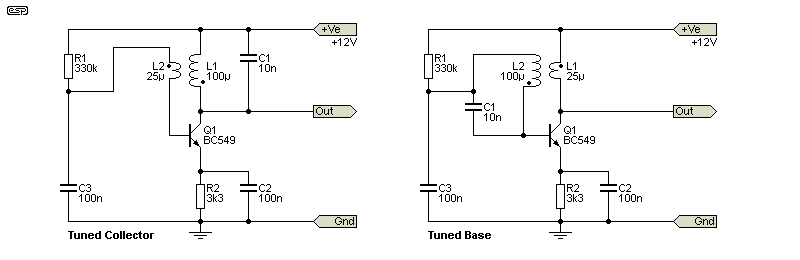
Figure 2.1 - Armstrong/ Meissner Oscillator
The Armstrong or Meissner design is really the 'grandfather' of all oscillators. Invented in 1912 by Edwin Armstrong and independently by Alexander Meissner in 1913, [ 3 ], this was the most important contribution to radio of all. Transmitters rely on an oscillator to provide a known frequency for transmission. Early (on-off only) transmitters used just a spark-gap, followed later by a tuned circuit excited by a spark gap or a high frequency alternator, but the spark-gap transmitters were very wide bandwidth and could not be adapted for voice transmission. While theoretically possible, alternators were not used for voice transmission either.
like all LC oscillators, the Armstrong/ Meissner oscillator uses a tuned circuit. The location of the tuned circuit varies, and it can in the plate (for a valve) or collector (using a transistor), and a loosely coupled ('tickler') coil to provide feedback to the grid/ base. There are several variations, and in others, the tuned circuit is in the grid or base circuit allowing the tuning capacitor to be grounded. Note the coil's 'polarity' marks in Figure 2.1 - the dot signifies the start of the winding. The coils are loosely-coupled, meaning that they are usually wound side-by-side on the former (with a small gap between them). Amongst other things, this prevents a high degree of interaction between the two, and helps to reduce distortion. Determination of the tickler coil's turns and spacing from the tuned coil was done (usually empirically) in the design phase.
As with all of the designs shown, the amplifying device can be a valve, bipolar transistor, JFET or as part of a dedicated IC. In the simulation I ran, a JFET was the most stable, as the much higher gain of a BJT caused the circuit to misbehave. This was the only oscillator I simulated that was 'finicky' about the coupling between the coils, and if the coupling is too great the circuit has very high distortion. All others simulated pretty much perfectly from the outset, and required no tweaking. I suspect that 'real life' would be similar, one of the reasons the Armstrong/ Meissner circuit isn't used often any more.
In some cases (particularly when impedance matching was required), a third coil was used for the output. This could be close-coupled to L1, or use loose coupling to prevent unwanted interactions between the tank circuit and the 'outside world'. A separate output winding can be added to any of the circuits shown below as well.
While the Armstrong may be the grandfather of LC oscillators, it's been superseded for the most part. One reason is that it's sensitive to the coupling between the tuned circuit and 'tickler' coil, which isn't an issue in the circuits that followed. Stability is a very important parameter for an RF oscillator, because the frequency is high, and even a small drift (in percentage terms) means a large frequency change. AM radio stations are spaced only 9kHz or 10kHz apart, so a drift of a few kHz is the difference between your signal being received clearly, subjected to heterodyning (adjacent channel interference causing high-pitched whistles along with the audio) and/or not being picked up at the expected frequency. Prior to crystal oscillators being used, this would be a major problem if your transmitted signal changed frequency with time, temperature or whim.
If a transmitter drifts, everyone tuned in is affected, and that's a real problem. This is one of the reasons that temperature sensitive ceramic capacitors were developed, so that temperature changes wouldn't affect the tuning (for transmitters and receivers). Modern transmitter and receiver designs render these points moot for the most part, but these designs have mainly been evolutionary, not revolutionary. One thing that did revolutionise transmission and reception was the crystal oscillator, followed by digital synthesis, and these have made most LC oscillators a part of history. That doesn't mean that they are useless or pointless, as it's far easier to build a fully tunable LC oscillator than it is to put together a digital frequency synthesiser!
The basic Hartley oscillator is shown in Fig. 3.1. The total inductance is 100µH, with 10nF in parallel. The circuit oscillates at 159kHz, as determined by the inductance (L1) and capacitance (C1). The coil has a tap that is usually somewhere between 50% and 25%. The tap means that the signal to the base is inverted so it's in phase with the collector signal (positive feedback).
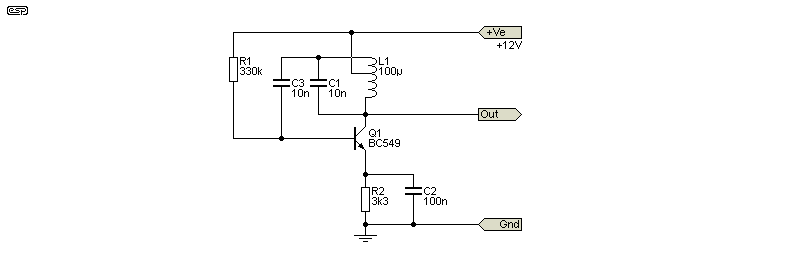
Figure 3.1 - Hartley Oscillator
The tap simply provides enough positive feedback to ensure reliable oscillation. Reducing the drive level into the base lowers distortion, which is important for many RF applications. The output level will be from (close to) zero to +24V due to the tuned circuit (an output of almost 8.5V RMS). The reactance of C2 and C3 is only 10Ω and 100Ω (respectively) at 159kHz. These caps can be made smaller for higher frequencies.
With a Colpitts design, a single inductor is used, with two capacitors, each with twice the required tuning value, to split the signal. The centre-tap of the tuning caps is grounded, and the resulting signal at the base is inverted, providing positive feedback.
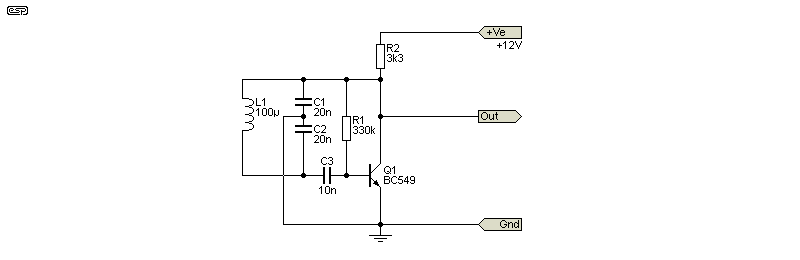
Figure 3.2 - Colpitts Oscillator
The collector load resistor (R2) may be accompanied by a RFC in series, to provide a higher impedance at radio frequencies. This isn't necessary at low frequencies such as 159kHz, but it helps as the fT (transition frequency) of the transistor is approached. As shown, the circuit is perfectly happy at up to 20MHz and likely beyond. The fT of a BC549 is around 100MHz if that helps at all. Expecting higher than perhaps 30-40MHz would almost certainly be unwise.
Tuning a Colpitts oscillator may seem like a challenge, but a common approach is to add a tuning cap in parallel with the coil. The tuning frequency is easily calculated, as it's based on the existing series caps in parallel with the tuning cap.
James K. Clapp published his design in ca. 1948, and provided a full paper on the oscillator in 1954 [ 3 ]. The formula to determine the frequency is more complex than the others, as it uses a combination of series and parallel capacitors in the tuned circuit. The circuit is also (and preferably) referred to as the Gouriet-Clapp oscillator, because the circuit was independently developed by Geoffrey Gouriet for the BBC in Britain in ca. 1938. The Gouriet circuit was not published until ca. 1947.
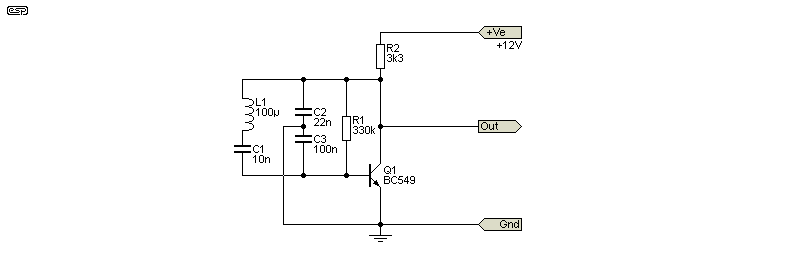
Figure 2.3 - Gouriet-Clapp Oscillator
Although the circuit is superficially similar to the Colpitts oscillator, the primary tuning capacitor is C1, is in series with the tuning coil. The frequency is also influenced by the series combination of C2 and C3. With the values shown, the effective capacitance of C2 and C3 in series is (roughly) 18nF, and the frequency is determined by the following formulae ...
Cp = C2 × C3 / ( C2 + C3 )
fo = 1 / ( 2π × √ L × C1 × Cp / ( C1 + Cp ))
fo = 198kHz for the example shown in Fig 2.3
If (for example) C2 were reduced to 47nF, the series combination is 14.98nF (15nF is close enough) and the frequency is increased to 205.5kHz. This has been verified by simulation, with the calculated and simulated frequency being almost identical. While the tuning frequency is more difficult to calculate, the Gouriet-Clapp circuit has the best frequency stability of the three major types, so is a very good choice. The two parallel caps (C2 and C3) must be high-stability types. The ratio between them is somewhat arbitrary, but common usage indicates that it will be within the range of 2:1 to 5:1, with the upper capacitor (C2) being the smaller of the two.
It may seem odd to use an emitter follower (or any other device including a valve). The follower circuits have a voltage gain of less than unity (typically between 0.9 and 0.98). The small loss is easily compensated though, since it's easy to make the tuned circuit have the necessary gain to ensure oscillation. Followers have an advantage, in that the output impedance is low, making it easier to drive following circuitry.
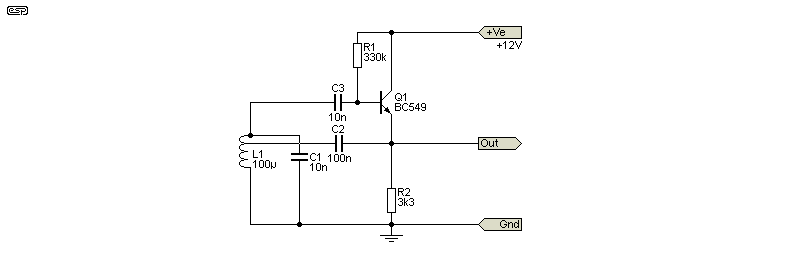
Figure 3.1 - Hartley Oscillator (Follower)
An emitter-follower Hartley oscillator is shown above, and the tuning coil provides the necessary voltage step-up via transformer action. As before, the tapping point is around 25%, so the AC voltage at the base of Q1 will be greater than the voltage at the emitter. The idea is to provide enough step-up via transformer action to get reliable oscillation, but not so much that the transistor is overdriven, as that will cause excessive distortion.
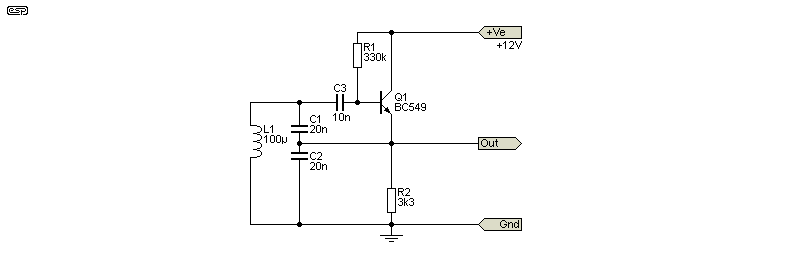
Figure 4.2 - Colpitts Oscillator (Follower)
For a Colpitts oscillator using the tapped capacitance, we get the same step-up action as before. This will require you to perform some calculations or experiments, as it may not be immediately apparent. The capacitors are normally equal, providing a (nominal) 2:1 step-up. While this may seem excessive, it usually works well enough in practice.
The most common tuning method is to use a variable capacitor. Examples can be found in older (valve or transistor) radios. You can still get them, but most now use a plastic film dielectric which is must less stable than air. The advantage is that the capacitor is a lot smaller for the same capacitance. Some are seriously expensive, particularly anything classified as 'vintage'. Most AM radios used a dual-gang variable capacitor, with one section used for the local oscillator and the other to tune the incoming RF signal.
There's a 'gotcha' when tuning an oscillator. If the capacitance (or less commonly the inductance) is changed, the frequency is changes as expected, but so is the tuned circuit's Q. You should recall from Section 1 that the resonant frequency occurs when capacitive and inductive reactances are equal. If one is varied, the effective impedance of the circuit is altered, so the Q and (by implication) amplitude are affected.
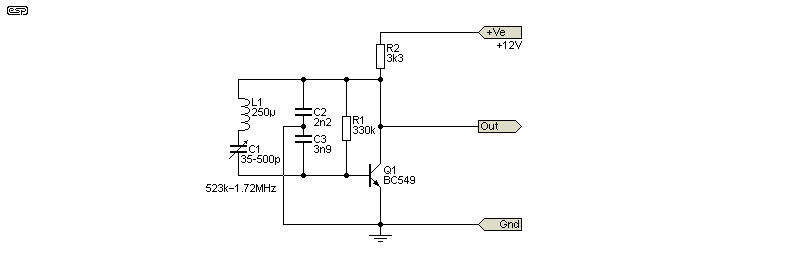
Figure 5.1 - Variable Gouriet-Clapp Oscillator
Note that I made no attempt to optimise the above circuit, other than to provide values that allowed it to oscillate across the range shown. With an output frequency of 523kHz the amplitude is 5.12V RMS, falling to 3.27V (RMS) at 1.7MHz. The variable output level was (comparatively) easy to cure with valves, because many were available with a 'remote cutoff' grid construction, meaning the gain could be varied by changing the bias (this was also used for AGC - automatic gain control).
In most cases, the range needed isn't particularly great, as AM radio only spans the frequency range from 530-1700kHz (this differs slightly by country). That's a ratio of 3.2:1, and while the oscillator level will vary, manufacturers made an effort to minimise the amplitude variation. This article isn't about AM radio receivers though, so I won't be providing any more detail. All of the oscillators shown above can be made variable, but the Colpitts is harder than the others because there are two capacitors. A small frequency variation is possible by changing only one cap, but it's not a common approach. As noted above, it's more common to reduce the value of the series caps, and place a variable capacitor in parallel with the coil.
As noted above, a crystal (aka xtal) is an electro-mechanical resonator, using quartz as the piezoelectric medium. They have extremely high Q (up to 3,000 is common), and consequently very good frequency stability. Where necessary, crystals are housed in a temperature controlled mini-oven (OCXO - oven controlled/ compensated crystal oscillator). A variation is the TCXO - temperature compensated crystal oscillator (the term TCXO is sometimes used to describe temperature controlled crystal oscillator). The frequencies available range from a few tens of kHz up to about 200MHz, but that's at the extreme end. Without compensation, the frequency drift is typically around 0.6PPM/°C (just over 1 second per month).
In modern circuits, there is often provision for direct connection of a crystal to the IC (many microcontrollers have this feature). The necessary circuitry is internal, and only requires the connection of the desired crystal and (usually) a pair of loading capacitors. These can often be 'tweaked' to pull the crystal frequency a little - the range is small though. The most common 'cut' applied to crystals is known ass the AT-cut. I don't propose to go into details here, as there's a great deal of information elsewhere.
One of the most common circuits is the Pierce oscillator, using a CMOS inverter. The feed resistor (R1) is commonly left out, as a CMOS inverter has enough output resistance to limit the drive level to a safe value. C1 and C2 depend on the crystal itself, and datasheets will usually provide the optimum value for a given crystal. The range is typically between 10pF to 100pF, but higher values are sometimes used. In some cases a trimmer capacitor is used (usually in place of C1) to allow a small amount of variation. Some CMOS ICs will require R2 to force the inverter into 'linear' operation, but this is usually not needed. If included the value will typically be at least 1MΩ.

Figure 6.1 - Xtal Equivalent Circuit And Basic Pierce Oscillator
The values in the equivalent circuit are ... unusual, and would never be found in a 'traditional' tuned circuit. The inductance is very high (250mH) and the capacitance extremely low (40fF - femto-farad, or 0.04pF), but be aware that these are not physical values, but are used for modelling the crystal's behaviour. The high inductance and low series resistance contribute to a very high Q, with the circuit shown resonating at 1.59MHz with a Q of around 50,000!
Because there is so much available material for crystal oscillators (and Reference 7 is recommended reading) I don't intend to go any further on this topic. Crystal oscillators are mentioned here simply because the crystal itself is equivalent to a series resonant circuit, with the crystal providing the inductance and capacitance. Today, these are probably the most common radio frequency oscillators used, because they remove the tedium of winding coils and perfecting circuits to get acceptable frequency stability.
Of course, crystals aren't perfect, and this is particularly true for the 32.768kHz crystals used in quartz clocks. The cheap movements are often less accurate than a decent mechanical clock, and they have fairly poor temperature stability and initial accuracy. It used to be that (quality) quartz clocks were very accurate, but those are now consigned to the dustbin of history.
Although LC oscillators aren't used for 'true' audio applications, they are still an important analogue building block. Since radio is intended for audio, the topic is relevant. Even if it weren't, oscillators in general are an interesting topic, and while you may not need to use an LC oscillator any time soon, knowing the basics of how they work is an important part of general electronics knowledge. RF circuits seem rather mysterious to many people, and sometimes they seem to defy the laws of physics. They don't, but RF is a very different world from that of audio.
This article is intended only as a short introduction to the world of RF oscillators. While countless hobbyists have built oscillators, this is often an unwanted byproduct. Any time you have sufficient positive feedback (due to excessive gain, poor shielding between preamps and power amps, etc.) you risk creating an oscillator. Its frequency won't be stable or predictable, because there's no defined resonant circuit, other than by accident. Audio oscillators are very different, and many examples are shown in the article Sinewave Oscillators - Characteristics, Topologies and Examples.
Radio would never have been possible without the contributions of the early pioneers who devised the circuits described here, and (as always) a great deal of the development was done to facilitate telephone systems, which were the basis of all modern electronics. As with many other articles, this one is not something you'll need very often, and many in electronics will never need to know anything other than how to construct a crystal oscillator. Even that's becoming uncommon, as most microcontroller boards have already done the hard work, and all that's left is to provide power and some code, along with interfaces to the outside world.
1 Ceramic Capacitor Data (Tecate Group)
2 Superheterodyne Receiver (Wikipedia)
3 Armstrong oscillator (Wikipedia)
4 Frequency Stable LC Oscillators (JK Clapp)
5 Oscillators (Oregon State)
6 LC Oscillators (Modern Ham Guy)
7 Crystal Oscillator Circuits (Robert J. Matthys)
8 Crystal Oscillators (Prof. Ali M. Niknejad, University of California, Berkeley)
9 AWV Radiotron Designers Handbook (Edited by F. Langford Smith. 1955)
 Main Index
Main Index
 Articles Index
Articles Index