

|
| Elliott Sound Products | Heatsinks And Amplifiers |
 Main Index
Main Index
 Articles Index
Articles Index
The question posed above - "How much heatsink do I need for an amplifier?" is right up there with "How long is a piece of string?". There's no simple answer, and no simple way to work out the answer. The answer itself (to both questions) is "it depends". In fact, the answer depends on quite a few factors, and some may be imagined to be fairly complex. Although they can be simplified, there are quite a few things you need to consider.
Trying to determine how big a heatsink should be for any given amplifier seems to be something that most DIY people try to avoid. This is probably with good reason, because it's not especially easy to work out. We also need to look at various amplifier classes (e.g. Class-A, Class-B, Class-D, etc.), and each is unique in terms of the heatsink needed. It's pretty much a given that Class-A needs the most, and it's also the easiest to calculate. Class-B (or Class-AB) is somewhat trickier, and Class-D can be quite difficult when all characteristics are considered.
In this short article, you will only get some basic guidelines. There is a great deal more that you will need before you can make a complete and accurate calculation, and often physical testing can be the only real way to know for certain. If you haven't done so already, I recommend that you read the article Heatsinks - selection, transistor mounting and thermal transfer principles. This is a very comprehensive article, and should be considered essential reading.
There are some assumptions used here, the first being that the air temperature available to the heatsink is at 25°C, and that the maximum allowable average transistor die temperature should not exceed 85°C. Cooler is better, but that can get expensive. I've also assumed that music will be the source, and that it has some dynamic range, so even if the amp is driven to just below clipping the long term average output power will typically be no more than 10% of the full power available from the amp. That assumes a peak to average ratio of 10dB. You'll find that this is not an area that's well covered on the Net, and there's surprisingly little information available that tells you just how much heatsink you need for a given amplifier. The peak to average ratio is also known as crest factor. (I will mention in passing that the crest factor of a sinewave is 3dB (a ratio of 1.414:1), but it's generally irrelevant and is not a useful parameter.)
By far the biggest single problem is trying to determine how much power an amplifier will dissipate, based on the power delivered to the load. Ultimately, it depends on a great many factors, such as the amplifier's maximum power, how loud you will be listening, the type of programme material and the loudspeaker's impedance. There are no simple answers, but I will try to provide solutions that will be quite acceptable for most home listening. For professional audio (including large scale PA systems) hopefully the amp designers have already provided heatsinks that will handle the power, and almost all use at least one fan, often two or more. Forced air cooling requires testing to determine the effective thermal resistance.
It's very important to make this point ... There is no such thing as a heatsink that's too big. Using a heatsink that's bigger than necessary means that it's physically larger and more expensive, but an oversized heatsink will never cause an amplifier to fail.

| It's imperative that you are aware that this article discusses average output device dissipation only. Safe operating area of the output devices is not included, and is a completely separate part of the design process. For more information on this topic, see Transistor Safe Operating Area and Phase Angle Vs. Transistor Dissipation. Peak dissipation and average dissipation are separate design processes, and one does not predict the other. |
This article is not meant to provide a single 'definitive' figure for the size of a heatsink. The guidelines here may over or under estimate the actual power that needs to be dissipated by the heatsink, and there is simply no way that a single figure can ever be used with any amplifier. The programme material, actual (vs. rated) speaker impedance, loudspeaker efficiency, use of compression or limiting and just how loud the sound needs to be are variables that cannot be predicted. Designing for absolute worst case will result in a heatsink that's larger and more expensive than necessary, and its capabilities may never be utilised. Designing for a (perhaps utopian) 'ideal' case will result in a heatsink that's too small. Like everything else in electronics, the heatsink will be a compromise.
An anecdote is appropriate here. A chap approached someone I know with the claim that the heatsink on an amp he had built was too large. He came to this conclusion because the transistors were very hot but the heatsink was almost cold. Therefore, by his reasoning, the heatsink was obviously too big because it didn't get hot enough. Reality was different of course. The problem wasn't that the heatsink was too big (there really is no such thing), but that the transistor mounting was abysmal and the thermal resistance between transistors and heatsink was much too high. This is a critical part of the assembly, and the lowest possible thermal resistance between case and heatsink is essential for maximum power handling.
The first thing that must be considered is the thermal resistance (often written as θ) of the entire thermal path. This means the effective resistance between the transistor (or IC) die and the ambient air. The ambient air temperature is not the temperature of the air in the room, but the temperature of the air at the heatsink's surface. If the heatsink is in a hot environment, then that temperature is what has to be considered. No heatsink should be operated where it can't get free airflow, because that will increase the temperature of the heatsink, and ultimately the transistor (or IC) case and the internal die. Most of the examples that follow will assume that the amp's heatsink has access to free air at no more than 25°C.
Thermal resistance (θ) includes the quoted figure from the manufacturer between the die and case, the insulating medium you use between the device's case and the heatsink, and the heatsink itself. See the heatsink article for some very detailed information about the various thermal transfer materials. There are several different ways you can insulate the transistor or IC case from the heatsink, and the most common are shown in the following table.
| Material | Thermal | Electrical | Thermal Resistance | Other Properties |
| mica | Good | Excellent | ~ 0.75 - 1.0 °C/W | Fragile |
| Kapton | Good | Excellent | ~ 0.9 - 1.5°C/W | Robust (but very thin) |
| aluminium oxide | Excellent | Very Good | ~ 0.4°C/W | Fragile - easily damaged |
| Sil-Pads | Fair + | Excellent | ~ 1.0 - 1.5°C/W | Convenient |
The above is simplified, and is based on the TO-220 case style. Larger cases will have a reduced thermal resistance, directly proportional to the surface area. For example, if you use a TOP-3 (plastic version of TO-3) TO-247 or TO-264 case the area is more than double, so thermal resistance may be around half that shown in the table. However, this also depends on the transistor specifications and how well you can prepare the heatsink surface and insulating medium, and how the transistors are held down. Note that silicone pads in general are a very poor choice if you expect to dissipate more than a few watts. Manufacturer's claims and reality are usually quite different from each other!
There are countless variables, but for the sake of convenience we'll assume for the moment that the total thermal resistance between the die and heatsink is 3°C/W. That means that for every watt dissipated by the transistor or IC power amp (long term average) the die will increase its temperature by 3°C. This assumes that the heatsink remains at 25°C, but of course that cannot and does not happen in reality.
The heatsink has to be made big enough to ensure that the die temperature remains as low as possible. This is essential to ensure that the transistors safe operating area (SOA) will not be exceeded, even when the amplifier is driven at the worst case power level for an extended period. The SOA is temperature dependent, so hot transistors can dissipate less power than cool ones. Maintaining a fairly low die temperature also allows for instantaneous peak dissipation that's much higher than the average. The heatsink's thermal mass will ensure that the heatsink itself remains at a fairly stable temperature, but the die temperature will fluctuate widely during operation.
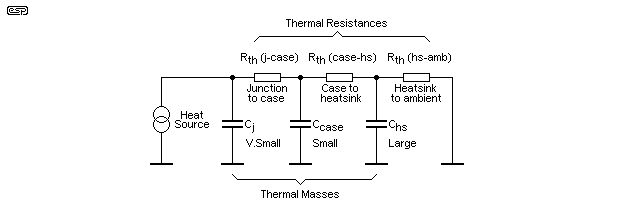
Figure 1 - Thermal Path - Junction To Ambient (Schematic)
Figure 1 shows the thermal path that we need to look at. The heat source is the transistor or IC die, and the thermal resistances shown are the three that need to be taken into account. The capacitors show the thermal mass of each component in the chain. The junction's thermal mass is tiny and can be ignored, as can the thermal mass of the case. The heatsink's thermal mass will usually be significant, and it's very important as it allows short bursts of very high power to be absorbed quickly, so only the average power needs to be considered.
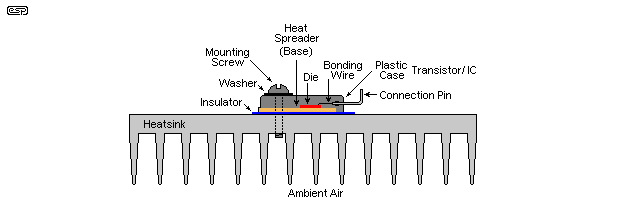
Figure 2 - Thermal Path - Junction To Ambient (Physical)
This drawing shows the thermal path in more familiar form. It shows the interfaces in their physical form rather than a schematic. The end result is the same - there is thermal resistance at each interface because none of the materials is a perfect thermal conductor, and no interface between materials can be perfect. The heat spreader is the metal part of the semiconductor's case with flat-pack devices, and it's usually nickel plated copper or similar. TO-3 style devices use a steel case, with an internal copper 'coin' or heat spreader between the die and case itself. It's notable that most counterfeit transistors have the die attached directly to the steel case, resulting in much higher thermal resistance (steel is a very poor thermal conductor).
You can't directly change the junction to case thermal resistance, but you can improve matters by using parallel transistors, or using transistors with a higher power rating than are strictly necessary for normal operation. This isn't required for low to medium power (up to 100W amplifiers), but becomes critical as power increases. Running any transistor to the limits (or beyond) its rated instantaneous dissipation is a recipe for disaster, and this includes its rated safe operating area (to avoid second breakdown failure).
Most heatsinks are a fairly heavy mass of aluminium, and the thermal mass is usually quite high. While the die will experience short duration sudden temperature increases and decreases, the heatsink will rise to a stable temperature depending on the average power being dissipated. A heatsink can remain almost cold for a period of time, and it heats up fairly slowly if designed conservatively.
 | One thing you need to be aware of is the nature of a heatsink's thermal resistance. When it's specified by
the manufacturer or supplier, the operating temperature is rarely provided. This is most unfortunate, because you really do need to know at what surface temperature
the claimed thermal resistance is valid. As the temperature differential increases, the thermal resistance falls. A heatsink operating at 100°C in an ambient temperature of 25°C will show a thermal resistance that's a great deal better than it will be at (say) 50°C. Because few suppliers ever tell you the operating temperature you already have an unknown quantity that will affect all subsequent calculations. |
The location and orientation of the heatsink also affects the thermal resistance. Unless you are using a fan, convection is the primary cause of air movement. The fins must be vertical so air can pass between the fins with the minimum possible interference. Anything with a heatsink should never be housed in a cabinet or any other enclosure that prevents free air movement into the room. Remember that the ambient temperature is the temperature of the air in the immediate vicinity of the heatsink, and this can be quite different from the room temperature.
Enclosing the heatsink in the cabinet is a really bad idea, unless there are large ventilation slots above and below the heatsink(s). This also means that the cabinet needs substantial feet to keep it off the surface upon which it's standing. You also can't place anything on top that will impede ventilation. Fans can be used, but you still need ventilation slots. Hot air must be able to escape the enclosure, and fresh cool air needs to be able to get in.
Placing all the power transistors right next to each other might look nice and be the most appropriate electrically, but it does nothing good for getting rid of heat. Power transistors (or other heat sources) should be spread across the heatsink area as much as possible, but remaining a sensible distance from edges and ends. The heat from each device has to be conducted through the aluminium, and because it's not a perfect thermal conductor the metal will be hotter directly behind the heat source.
The top of the heatsink will nearly always be slightly hotter then the bottom, because the air received (by convection) has already passed by the fins at the bottom, and is therefore hotter at the top where it exits. The thermal gradient is usually quite small, and can be discounted if the devices are all (more or less) mounted along the centre line.
If you haven't done so already, please see the article about Heatsinks. This knowledge is invaluable before you start, and it would not be sensible to repeat it all here.
The easiest amplifiers to calculate for are Class-A designs, because the dissipation is close to constant regardless of load. If the power supply is 30V and the current 1.5A, then the dissipation is simply 1.5A x 30V = 45W. Multiple devices will make it easier to keep the die temperature low, but it doesn't really matter if that power is dissipated in one or ten transistors, the total power is still the same. There are other considerations such as the thermal resistance between the transistor dies and the heatsink itself, but we'll look at that a little later. Before you start you'll need to decide on an appropriate maximum transistor die temperature. I suggest around 85°C if possible.
If we have to dissipate 45W and we don't want the heatsink temperature to exceed (say) 40°C in a 25°C ambient, then the heatsink's thermal resistance needs to be ...
Tr = 40 - 25 = 15°C
Rt = 15 / 45 = 0.33°C/W
Where Tr is the temperature rise and Rt is thermal resistance
Now we can factor in the thermal resistance between the transistor die(s) and the heatsink. With a pair of transistors they'll operate at half power - 22.5W for each. If the thermal resistance between die and heatsink is 2°C/W (difficult but achievable for high power devices mounted with care), each die will be 45°C hotter than the heatsink which we decided should run at no more than 40°C. The die temperature is simply the heatsink temperature plus the temperature rise across the case and mounting. The thermal gradient will be ...
Ambient = 25°C
Heatsink = 40°C
Junction = 85°C
With this amount of dissipation, it will be difficult to maintain the junction temperature at a maximum of 85°C unless the heatsink temperature is kept to 40°C or less. If the thermal resistance between the junction and heatsink is greater than 2°C/W you may end up with an impossible situation. For example, if the thermal resistance between junction and heatsink increases to 3°C/W, the heatsink would have to run at no more than 17.5°C - clearly impossible if the ambient is 25°C. The only alternatives are to allow the junctions to run hotter than the (hoped for) target figure or reduce the effective thermal resistance between the die and heatsink.
If more transistors are used, the heatsink temperature will remain the same, but each transistor die will run cooler. Each device still has the same thermal resistance from die to heatsink, but the power dissipated is reduced. These relationships are actually quite simple once you get your head around them. For example, if the amp dissipation is shared between four transistors instead of two, each will dissipate 11.25W instead of 22.5W, and the die temperature rise is reduced to 22.5°C, or just under 34°C if the thermal resistance is a more realistic 3°C/W between die and heatsink. This allows a smaller heatsink to be used, or means lower die temperature for the same heatsink. Lower operating temperature should always be a design goal, but is not always possible.
When the amp does not dissipate a constant power the calculations become harder. Since this describes the majority of amps in use (most commonly Class-AB), there are many decisions to be made. Quiescent current is usually fairly low, no more than 100mA in most designs and usually a lot less, so quiescent dissipation is easy to calculate. If the supply voltage is 70V (±35V) then the dissipation is 7W at the maximum quiescent current of 100mA, and will usually be lower than that.
The next graph shows peak output voltage and dissipation of one half of a Class-AB power amplifier. This shows the peak power in the positive output transistor with a 4 ohm resistive load, and the negative transistor has the same dissipation for negative-going half cycles. At exactly half the +35V supply voltage (17.5V), the transistor dissipation is at its maximum, 76W. The average dissipation in each output transistor is 22.7W at the onset of clipping. The situation changes with a reactive (loudspeaker) load and the peak power increases (as much as double), but the average remains much the same. This is discussed in more detail in the article Phase Angle Vs. Transistor Dissipation.

Figure 3 - Instantaneous Dissipation Vs. Output Voltage
If the amp will be driven fairly hard, a reasonable approximation for dissipation might be 50% of the output power. If the amp runs from ±35V and is driving a 4 ohm load, output power will be close to 100W, therefore total dissipation will be just under 50W. This is a worst case figure that will not be reached in practice, and it's common in commercial designs to only allow less than half that because music is dynamic and full power is never continuous. Knowing that a long term average dissipation of 25W is reasonable (if overly generous), the heatsink can be determined easily, using the same method as described above. If we can allow a maximum heatsink temperature of 60°C, we get ...
Rt = 35 / 25 = 1.4°C/W
That figure is for a single amplifier, and power dissipated is naturally double for a stereo amp, so the heatsink's thermal resistance should be 0.7°C/W for a stereo pair of amps. In most cases this may still be considered overkill, but if you design for the smallest possible heatsink, then it's a very good idea to include an over-temperature cutout, or a thermo-fan that will turn on if the heatsink temperature rises above a preset limit. An example calculation is shown below and is from an ST Microelectronics application note [ 1 ].
Pd = V² / (( 2π )² * RL )
(Where V is the total supply voltage, Pd is total dissipation and RL is the load resistance in ohms)
For example, for the same amp described above (±35V supplies, 4 ohm load) ...
Pd = 70² / (( 2π )² * 4 ) = 31 Watts
The dissipation calculated as above is for the complete output stage, so the average dissipation of each output transistor is half that calculated. The figures derived using this formula are in reasonable agreement with the table shown further below, but are a little more optimistic (i.e. the dissipation is somewhat lower than my table shows).
If the amp is rated at (say) 20W/ channel, then you need to allow for a dissipation of up to 5W continuous. If the amplifier is a small 'chip amp' such as the LM1875, this has a TO-220 case. Therefore the heatsink has to be bigger than you think, because the IC's thermal resistance from die to heatsink is a lot higher than a pair of discrete transistors. In this instance, I suggest that the heatsink needs to be designed based on a dissipation of 10W, not 5W, so it should be about 3.5°C/W for each IC. A cooler heatsink allows for a higher temperature rise between the heatsink and transistor or IC die, while maintaining the die temperature at (or below) 85°C.
I took some measurements of a music source (FM radio) to determine the worst case peak to RMS (or average power) ratio one can expect. The type of music is largely irrelevant due to original material compression plus that added by most FM radio stations. What I was doing was obtaining a figure that can safely be used to determine the dissipation that one can expect from any given amplifier used with the worst possible input signal. Programme material with greater dynamic range requires less heatsinking.

Figure 4 - Worst Case Signal Waveform
The waveform is shown above. The peak amplitude is ±800mV and the RMS voltage is 342mV. The peak to RMS ratio is therefore about 2.35:1 or 7.5dB. This does change though, because 'infinite' compression is neither possible nor desirable, and over a period of a few minutes I saw the RMS voltage go as low as 250mV - the peaks were unchanged. The RMS voltage can also be higher than the 342mV measured, but not by a great deal. On average and taken over a reasonable period with different tunes playing, the peak to average ratio was 2.5:1 - a ratio of 8dB. For a hypothetical 100W amplifier, the average power is about 16W when the amp is driven to just below clipping.
When an amplifier is driven with a sinewave to just below clipping, a suitably pessimistic assumption is that transistor dissipation (two devices in push-pull) is roughly 50% (both devices) of the power delivered to the load. The worst case is to run the amplifier at half output voltage (one quarter of full power), when the total transistor dissipation will be close to double the power delivered to the load. A 100W amp operating at 25W continuous will dissipate about 50W as heat. If the RMS output voltage is higher or lower than half of the maximum, output stage dissipation is reduced.
We don't listen to sinewaves, so the peak to average ratio determined above should be used. This provides a reasonable determination of the likely average power needed. This can be difficult because there are too many unknown factors. You can't design a heatsink based on how you think an amplifier will be used, because others will use it differently. If we use the signal I captured as a possible 'typical' signal, when an amplifier is at the onset of clipping the RMS voltage will be around 0.4 of the maximum possible, close enough to the half voltage point where dissipation is at its maximum.
By that reckoning, a 100W amplifier needs a heatsink capable of dissipating up to 40W when driven by the waveform shown above and when driven to the maximum undistorted power. Fortunately, reality is different from worst case and the long-term average will be usually somewhat lower than calculated by using absolute worst case measurements. It's generally safe to assume the peak to average ratio to be 10dB, so the average output power will be 1/10th of the peak output. The average output power from a 100W amp will be around 10W, and total transistor dissipation will be 30W.
These general principles apply regardless of whether you have a discrete or chip (IC) power amp. If a 50W IC amplifier is running at just under clipping with normal programme material, the average output power will be about 5W and the IC's average dissipation will be around 15W. Now we have enough information to devise some rules to allow the appropriate heatsink thermal performance to be worked out.
Class-D amplifiers are a special case, and there are no simple methods you can use to calculate the dissipation. The switching MOSFETs have two (or perhaps three) different ways they can generate heat. The first (and simplest) of these is the power dissipated as a result of load current and the MOSFET's 'on' resistance (RDS-ON). If 5A flows and RDS-ON is 0.1 ohm, then the MOSFETs will dissipate about 250mW each (average), which is easily handled.
Because no MOSFET can switch instantly, there is a very brief period where the MOSFET has a significant voltage across it, as well as current through it. The instantaneous peak dissipation can be very high, but it lasts for less than a micro-second or so and the average is low. Just how low depends on the design of the circuit, and the ability of the drive circuit to source and sink the current demanded by the MOSFET's gate capacitance.
The third problem should not happen, and is commonly known as 'shoot-though'. This is a situation where the two MOSFETs conduct at the same time, which can raise the average dissipation to destructive levels. Although this is never intended, it may occur if the MOSFETs get too hot. At this point, failure is perhaps only milliseconds away. For this reason, it's essential that Class-D amps have an adequate heatsink.
Unfortunately, there is no easy way to work out the dissipation of a Class-D amplifier. If the designer or manufacturer provides the information you need then it's simple enough, but if not you will only know by testing. During any test, it's very important to ensure that the MOSFETs run as cool as possible to prevent thermal runaway due to RDS-ON. It's made very clear to most MOSFET users that RDS-ON increases with temperature and thus forces current sharing with parallel devices, but the downside is that as RDS-ON increases, so does the dissipation when the MOSFET is on. Increased dissipation leads to higher temperature, increasing RDS-ON and increasing dissipation. I think you can figure out what comes next.
It's a very good idea to keep MOSFETs as cool as possible, and fortunately with a well designed Class-D stage that's not especially difficult. You also need to be aware that some low cost Class-D modules (in particular those from Asia) have barely adequate heatsinks, and may self destruct if operated at maximum power for long periods.
Firstly, it must be understood that if a heatsink operates at 50°C with 25°C ambient air temperature, the heatsink's allowable temperature rise is 25°C. With no power being dissipated, the heatsink will already be at the room's ambient temperature, so in all calculations the ambient temperature has to be subtracted from the maximum allowable heatsink temperature, to obtain a figure for temperature rise.
Next, we need to work out the maximum acceptable transistor or die temperature. I recommend that 85°C is a sensible maximum, as most semiconductors still have a reasonable allowable dissipation at that temperature, and it's not so high that reliability is likely to suffer too much. IC power amps are different from discrete designs, because all the parts (power and driver transistors, etc.) are located in the same package, and the total thermal resistance will be higher as a result. On average, you might expect that the thermal resistance between the die and heatsink will be about 2°C/W (although that's actually optimistic), so if the maximum power is 50W and average dissipation is 15W then the temperature gradient will be 30°C.
Die temperature = heatsink temperature + thermal gradient ... or ...
Heatsink temperature = die temp. - thermal gradient
HS temp. = 85° - 30° = 55°C
We have 55°C at 15W remaining, and we are allowing for an ambient air temperature (at the heatsink surface) of 25°C. That means that 15W has to be dissipated with a maximum temperature rise of 30°C, so the heatsink needed is 2°C/W for each amplifier. That is a fairly large heatsink, but it will be needed if the amp is run at between half and full power over an extended period. At continuous long term full power (programme), the heatsink will run at about 55°C.
However, for normal domestic applications, you'll (probably) get away with less than half the calculated thermal resistance. So a 3°C/W heatsink may be quite acceptable, even for a pair of IC power amps, but if the amps are driven to high power for an extended period they will probably shut down thanks to internal thermal protection. If the ICs don't have thermal shutdown they will likely fail if driven hard for any length of time.
The same general principles apply for amps with discrete output stages, but there is a benefit that we don't get with an IC amplifier. The total output stage dissipation is distributed because the output transistors are discrete. If the stage has two output devices, then each handles half the total dissipation. With four devices, each only handles one quarter. This makes it a lot easier to get the heat out of the semiconductor dies and into the heatsink.
A 50W discrete amplifier will still dissipate about 15W with programme material at full volume (without clipping). Each output transistor will handle half that - 7.5W. Assume the same thermal resistance from die to heatsink as before - 2°C/W. At 7.5W (each device), the thermal gradient is 15°C, the heatsink can now operate at up to 70°C and needs a thermal resistance of 3°C/W for each amplifier.
Note that using multiple transistors you can estimate the thermal resistance by dividing (say) 2°C/W by the number of output devices. For the above example, the total average dissipation was 15W, and with 2 transistors we can estimate the thermal resistance between junction and case at 1°C/W. The thermal gradient is unchanged at 15°C.
Much as I'd love to be able to provide a simple formula that would allow you to determine the heatsink size needed for any given output power, it's not possible to do so. However, based on the above calculations it's not particularly hard to work it out. Some assumptions are essential, and the heatsink needed for an IC power amp is actually larger than that for a discrete design of the same output power. You might have expected the reverse, but the IC has to dissipate the total power through a single junction to case - case to heatsink interface, so the thermal resistance is higher.
A very rough way to determine the thermal resistance of a heatsink is to use the following formula. It's not particularly accurate and doesn't consider the heatsink's thickness, temperature, thermal conductivity or surface treatment, but it will give you an idea ...
Thermal Resistance = 50 / √A Where A is the total surface area in cm²
See the Heatsinks article for a great deal more, and to look at more accurate ways to estimate the thermal resistance. Using the above, a piece of aluminium 50mm x 50mm will have a thermal resistance of ~7°C/W if both sides are exposed to ambient air (total area of both sides is 50cm²).
First, determine the maximum output power, based on the supply voltage and load impedance. Some common values are tabulated below. The figures shown are 'ideal' and do not include losses in the amplifier or power supply. Actual power levels will be between 10% and 20% lower than those shown, but the -10dB power needs to be calculated based on the values given because the supply voltage will not collapse by very much with a relatively low average power output.
I could have included a heatsink size for each of the amp ratings below, but it would have to be based on too many assumptions and would therefore be worthless. Instead, you have to make some calculations using the process described, and based on the number of output devices used. We've already seen that using multiple output devices reduces the size of the heatsink required, so that has to be a factor in the final calculations. You may also find that you can run the semiconductor die at more or less than the 85°C suggested. Everything makes a difference!
| Supply Voltage | 8 Ohm Power | -10dB Diss. | 4 Ohm Power | -10dB Diss. |
| ±15V | 14 W | 4.2 W | 28 W | 8.4 W |
| ±20V | 25 W | 7.5 W | 50 W | 15 W |
| ±25V | 39 W | 11.4 W | 78 W | 23 W |
| ±30V | 56 W | 17 W | 112 W | 34 W |
| ±35V | 76 W | 23 W | 153 W | 46 W |
| ±42V | 110 W | 33 W | 220 W | 66 W |
| ±56V | 196 W | 59 W | 392 W | 118 W |
| ±60V | 225 W | 68 W | 450 W | 136W |
| ±70V | 306 W | 92 W | 612 W | 184 W |
| ±100V | 625 W | 188 W | 1.25 kW | 375 W |
The dissipation shown at -10dB is the total output stage dissipation, and includes the positive and negative transistors in each case shown. The output stage dissipation is based on a sinewave at 10% output power, roughly equivalent to -10dB average output voltage or power but deliberately slightly pessimistic. Output powers at or below 25W will often indicate an IC amplifier, and above that will usually use discrete output transistors. Supply voltages above ±35V will almost always involve a discrete output stage, and above ±42V there will usually be at least 4 output devices.
Note that the table assumes that the supply does not collapse under load, but that will almost never be the case in reality. If the unloaded supply voltage is ±35V, it's reasonable to expect that this will fall to about ±30V under load, especially with 4 ohm loads. As a result, the total dissipation (long term average) will usually be somewhat less than indicated. This means that the table is a little pessimistic, and means your heatsink may be a little bigger than is strictly necessary. This is much better than making it too small!
If the amplifier uses a single IC, assume at least 3°C/W from junction to heatsink, and the entire power dissipation shown in Table 2 will be dissipated in the IC package. I included the supply voltage because that determines the maximum output power and total dissipation.
For amplifiers with discrete output devices, assume 3°C/W for each device, and the dissipation shown is shared between the devices. If dissipation is 34W (±56V, 4 ohm load) it will probably be shared between 4 devices, so each will only need to dissipate an average of 8.5W which means a temperature rise of 25.5°C for each device. If we allow a die temperature of 85°C, the heatsink temperature can be as high as 60°C, and needs to have a thermal resistance of 1°C/W. A bigger heatsink means the devices will run cooler and is preferred, but the one calculated will most likely be fine for home listening.
To work out the heatsink's thermal resistance, we use exactly the same method as described earlier. First, measure, calculate or obtain from Table 2, the amp's power rating and supply voltage. Determine the average dissipation based on 1/10th (-10dB) full power. Dissipation is approximately the -10dB power level multiplied by 3. For example, a 70W into 4 ohms amplifier delivers 7W at -10dB. Average dissipation will be 7 x 3 which is 21W.
Power dissipated = ( max power / 10 ) * 3
Pd = ( 70 / 10 ) * 3 = 21W
Now you must consider the total thermal resistance between the junction and heatsink. For a single device (an IC amplifier), all the power is dissipated in a single package, and the thermal resistance will be ~3°C/W. For two transistors, each dissipates half the total, and the total equivalent thermal resistance is 1.5°C/W - assuming 3°C/W thermal resistance for each device. The temperature gradient is 31.5°C.
Die temperature = heatsink temperature + thermal gradient ... or ...
Heatsink temperature = die temp. - thermal gradient
HS temp. = 85° - 31.5° = 53.5°C
Now that you know the heatsink temperature, subtract the ambient (25°C) and work out the heatsink's thermal resistance.
Hs rise = HS temp. - 25°
Hs rise = 53.5° - 25° = 28.5°C
Rth (Hs) = Hs rise / Power dissipated
Rth (Hs) = 28.5° / 21W = 1.36°C/W
This is the heatsink's thermal resistance needed to satisfy the criteria set. The figure is an approximation, but errs on the side of caution. A slightly smaller heatsink will more than likely suffice for all normal listening, but should still provide a reasonable performance if the amp is pushed hard. It also helps that the thermal resistance of any heatsink improves (becomes lower) as the heatsink temperature rise above ambient increases.
One thing that you don't know is how the heatsink manufacturer arrived at the published thermal resistance in the first place. Was it done with the heatsink at 25°C above ambient? 50°C above ambient? More? We don't know, because this is rarely provided, so by assuming the worst (or designing with caution) there's a fighting chance that your amplifier will survive normal use, as well as the occasional party where it will probably be abused fairly heavily.
The only way to know for sure what the thermal resistance is for the designed maximum temperature is to test it.
We also need to consider the load impedance. A loudspeaker is not resistive, and the impedance varies with frequency. The nominal impedance is simply a reference to the average impedance across the frequency range, although the way it's calculated (or guessed) is often obscure. When an amp is driving a full range speaker system, the impedance at some frequencies will be lower than the claimed value, and at other frequencies it will be higher.
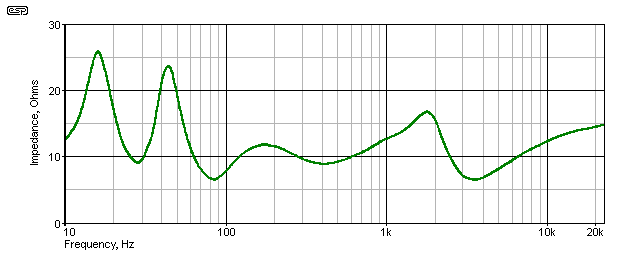
Figure 5 - Typical Loudspeaker Impedance Curve
The above shows a reasonably typical bass-reflex enclosure's impedance response. The double peak at the low frequency end is always present with vented boxes, and the impedance peak just below 2kHz is the result of the crossover network. This speaker has a nominal impedance of 8 ohms, but as you can see the impedance is only 8 ohms at 400Hz. Minima are seen at 85Hz and 3.5kHz at about 6 ohms or so. So even though the impedance would be classified as 8 ohms, over much of the frequency range it's quite a bit higher. The vent tuned frequency is at 28Hz (maximum output and minimum impedance at the extreme low end).
This does impose a reactive load on the amplifier, but because the impedance is much greater than the nominal, the amplifier's average dissipation is less than you would have thought. This means that dissipation is reduced over much of the frequency range. The effects are complex, but an amplifier driving a speaker load almost always has an easier time than if it's driving a dummy load of the same nominal impedance.
When designing the heatsink, you need to take into account the impedance variations of all speakers that are likely to be used with the amp. This is one of the reasons that dummy load tests at the minimum nominal impedance are important, as this will nearly always be a harder test than a loudspeaker. However, there are some speakers that are classified as 'difficult', often because of impedance dips that fall well below the nominal value. Whether these will cause an amplifier serious problems or not depends on how low the impedance falls and whether these dips are narrow or broad.
Narrow impedance dips can cause output devices to exceed their safe operating area at one or two frequencies, but generally don't increase the average dissipation by much. Broad dips in the midrange area in particular can increase the average dissipation significantly, especially if the amp is driven hard.
Ultimately though, it's not possible to design a heatsink to the absolute minimum and expect it to be able to handle every speaker system made. If that's what you need to do, then both the amplifier itself and the heatsink need to have adequate reserves to be able to handle the worst possible case. This increases the cost and size of the heatsink and the output devices. In reality, there aren't many speakers that cause great stress to most amplifiers, and some of those that do are probably best avoided anyway. If a speaker designer can't get the impedance right then it's possible that the response will be all over the place as well.
Although using a fan is a nuisance for a hi-fi amp, consider using a fan that only operates when (or if) the heatsink gets above a predetermined temperature. Project 42 is one method you can use. 99% of the time the fan will remain silent and the amp will be operating well within the output device limits. If pushed hard or used with material that has little dynamic range the fan will turn on only for as long as it's needed. Once the amp cools, the fan turns off again.
This allows you to use a heatsink that's somewhat smaller than necessary for continuous maximum output power, and that doesn't intrude unless it's necessary to protect the amplifier. You can also just use a bimetallic thermal switch attached to the heatsink, preferably as close to the output transistors as possible. Choose one with a temperature rating that's suitable for you needs - around 50-60°C will be fine for most amplifiers.
Even a small amount of forced air can dramatically improve a heatsink's thermal resistance, but it's something that must be tested thoroughly before you set up the amp and forget about it. Ensure that air is blown against the heatsink for maximum turbulence, and airflow must be directed so that it hits the heatsink close to where the transistors are mounted. Make sure that your thermal sensor/ switch is not in or near the airflow, or it may be cooled down faster than the heatsink and the fan will turn off before the heatsink is back to a sensible temperature.
A surprisingly large number of people get this wrong, including some manufacturers of high power amplifiers! Locating the thermal sensor close to the airflow means that it will be cooler than the majority of the heatsink, so transistors can run much hotter than intended. Do not be tempted to make the fan suck air away from the heatsink! This is another common error, and the fan's efficacy is seriously reduced by doing so.
Remember that if you use a fan, its airflow must not be impeded. For example, blowing air into a sealed box won't achieve anything useful, and there must be an exit point that will allow the maximum airflow possible. The exit should be at least as big as the fan, and if you include filters to prevent the electronics from being coated with fluff and dust, they have to allow good airflow and they must be kept clean!
Whenever you use a fan, consider including a thermal switch that will turn the amp off before it self-destructs. If the fan normally turns on at (say) 60°C, you might use a thermal switch that will shut the amp down if the temperature ever gets to 80°C, and that can only happen if the fan fails or its airflow is impeded.
A heatsink is not a device that can magically absorb heat from active components. It requires a lot of surface area so it can transfer the heat to the surrounding air, which itself should be as cool as possible. This means that there must be air circulation to the room. Air circulation within the enclosure is (almost) completely useless if the hot air can't be replaced by cool outside air. Many people make the mistake of adding vents on the bottom of a cabinet, but fail to include vents at the top so air can't circulate through the enclosure.
As noted at the beginning of this article, the answer to the question posed in the heading remains "it depends". The above provides some useful guidelines and hopefully will provide at least a reasonable starting point, but there are so many considerations that it is literally impossible to provide a single figure for heatsink size for any given amplifier. It's always better to err on the side of caution, and use a heatsink that may be a bit bigger than you really need. There really is no such thing as a heatsink that's too big.
Also, consider that a 100W amp running at 10W average power (just below clipping on transients) with speakers of typical sensitivity (say 87dB/1W/1m) will be generating an average sound pressure level (SPL) of 97dB at 1 metre distance. There are two amps in stereo and you will almost certainly be closer to 2m away, but the combined average in the room will still be at least 97dB SPL. That's pretty loud in the greater scheme of things, and hearing protection guidelines indicate for that SPL the maximum exposure in any 24 hour period is only 30 minutes.
Most of the time, power amps used for home systems will operate with an average power of around 1W or less. With fairly typical loudspeakers, 1W per channel will provide an SPL in the room of about 87dB. This might not seem like much, but it's a lot louder than normal speech. This means that in theory, most people could use 10W amplifiers and be perfectly happy, but it too limiting for anyone who listens to music with real dynamics. Most movie soundtracks also have a wide dynamic range and a reasonable amount of headroom is essential. 10dB is about right, which usually means around 100W per channel. At the average 1W or so listening level amp dissipation will be negligible, and often barely more than quiescent.
If the amp is pushed hard (well into clipping), that's theoretically better for the amplifier because the dissipation in transistors that are turned on hard is very low (see figure 4). For example, if a 100W amp is driven to the onset of clipping, the dissipated power is about 30W. If the same amp is overdriven by 10%, the output power increases to 115W and total dissipation falls to 26W. More clipping means even lower dissipation (but of course it sounds gross and places your speakers at risk). Note too that this only applies for a sinewave, and if music is playing you are likely to greatly increase the total dissipation when the amp is pushed into clipping on loud sections and transients. This is because the average power increases.
If the overall gain is increased to the point where an amplifier is clipping by 3dB (meaning that the input signal is 3dB too high), the average power is increased by roughly the same amount, so instead of the average power being at -10dB, it will be at -7dB instead. This can increase the output stage dissipation quite dramatically.
So, as noted at the beginning there are no simple answers. It's usually best to design around the estimates shown in Table 2. These are conservative and will generally give a fairly close approximation to the size of heatsink you should use based on average dissipation. You still need to work through the examples to arrive at a final heatsink rating in °C/W.
If you really must (for whatever reason) use a smaller than optimal heatsink, then include a thermo-fan so that if/when the amp is pushed hard it doesn't self destruct.
There are only two references because there is so little info on the Net, and the primary source of information was other ESP material as listed within this article, or obtained from measurements.
1 Dissipated Power And Heat Sink Dimensioning In Audio Amplifiers ICs - STMicroelectronics AN1965
2 The Effect Of Forced Air Cooling On Heat Sink Thermal Ratings - Crydom Inc.
 Main Index
Main Index
 Articles Index
Articles Index