

|
| Elliott Sound Products | Phase Angle Vs. Transistor Dissipation |
 Main Index
Main Index
 Articles Index
Articles Index
This article will help those who have built an amplifier that just blew up for no apparent reason. It will also help those who are planning to build an amplifier, either from the ESP projects pages or elsewhere. Contained herein are answers to questions such as "why can't I use the P3A amplifier at ±56V, or a single board P68 at ±70V". These questions are common, and it is always good to know why something is so.
For those who just don't understand exactly what 'speaker impedance' means, hopefully you'll get something from it too. A speaker is a reactive load. This means that it has resistance, and most of the time it also has either capacitance or inductance. These can be real capacitors and inductors, or simply the electrical equivalent of moving mass (speaker cones) and restoring forces (cone suspension, air pressure, etc.). Any moving mass translates to an inductance, and restoring forces ('springs') translate to capacitance. Resistance can be either real (electrical) resistance or friction. The loudspeaker's electrical phase angle is something that most people don't understand well, and the way it reacts with an amplifier is important.

| In general, we consider that the worst case power dissipation for an amp driving a resistive load is with one quarter of full power (half voltage) with a sinewave signal. While convenient, it's not strictly correct. An amp with ±30V supplies can produce 112W into a 4 ohm load, and at 15V peak input (10.6V RMS) output power is 28W. Dissipation (each transistor) is 21.3 watts. The (theoretically) correct peak output voltage is actually 0.637 of the supply - in this case 19.11V peak, or 13.51V RMS. Transistor dissipation rises to 22.27 watts. Given all the vagaries of an audio signal and the speaker load, this degree of precision is actually rather pointless. It is nice to know the exact figure, but we'll never need it for anything (and it only applies for a sinewave anyway!). |
While parts of this topic are also covered in the Safe Operating Area article, there is less amplifier design detail in this present version, making it somewhat easier to read - especially for novices. In this case, I have concentrated on the specific effects of phase, and once this is understood, I suggest that you tackle the 'full' version.
While it is generally understood that a typical loudspeaker has an impedance (as opposed to resistance), the implications of this are not widely understood. Many of the designs featured on The Audio Pages appear to be over-engineered, and the number of output devices seems excessive for the claimed output power.
This is entirely true! ... and for a very good reason ...
The problem with real loudspeakers is that they refuse to act like nice, well behaved resistors, and the impedance changes from being resistive, inductive and capacitive, depending on the frequency. Let's look at a typical 2-way loudspeaker system, whose equivalent circuit and impedance response are shown in Figures 1 and 2.
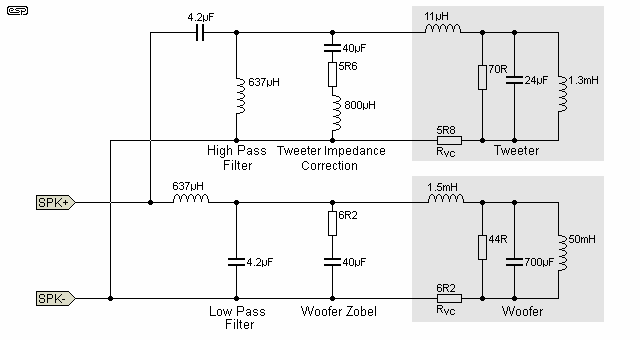
Figure 1 - Loudspeaker Equivalent Circuit
While it may look complex, it is simply a reasonable representation of a typical 2-way loudspeaker, having an impedance correction network to eliminate problems caused by the tweeter's resonance, and a basic Zobel across the woofer to damp the rising impedance cause by its voicecoil inductance. The crossover network is a conventional 12dB/octave parallel design. The speaker drivers are represented by the circuitry within the grey boxes.
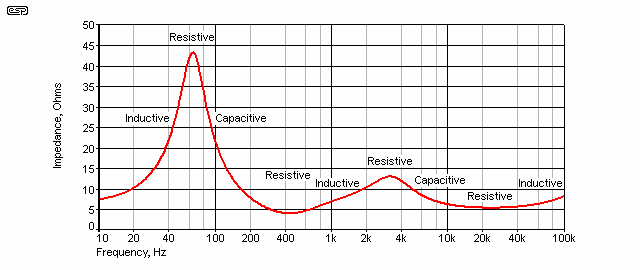
Figure 2 - Impedance Response of Simulated Speaker
Well below resonance, the system appears inductive, with the inductive reactance component rising with frequency as expected. At resonance, the load is purely resistive, and is at a relatively high value (typically from 20 to 50 ohms). Power at this frequency is very low - a 100W amplifier (8 ohms) will deliver less than 20W (19.6W to be exact) into an impedance of 40 ohms.
Above resonance, the load seen by the amplifier becomes capacitive, and impedance falls rapidly with frequency, eventually 'bottoming out' at some frequency (typically around 200Hz or so). This is the loudspeaker's 'nominal impedance' as quoted by the manufacturer. The impedance then starts to rise again as the voice coil (semi) inductance becomes significant. The crossover will almost always introduce further phase anomalies, and as you can see, any time the impedance changes, so too does the phase. The impedance is resistive at four frequencies only - 65Hz (woofer resonance), 430Hz, 3.2kHz (crossover frequency), and 23kHz.
As long as the impedance is predominantly resistive, the amplifier has a relatively easy job, with voltage and current in phase, and amplifier dissipation is at the minimum possible for a given output power. The problems arise close to resonance - either above or below, where the load is highly reactive, or anywhere else where the impedance changes. Note that a vented enclosure has a second low frequency resonant peak, and the amplifier sees exactly the same reactive loading around the peak introduced by the vent tuning.
The worst case is that the amplifier sees either pure inductance or pure capacitance. Under those conditions, the voltage and current output from the amplifier are 90 degrees out of phase. Fortunately, this never happens with a loudspeaker because there is always resistance in the circuit. This is a combination of the series resistance of inductor(s), voicecoil resistance and wiring - both internal and external (speaker leads).
As described above, the voltage and current into anything other than a resistive load will not be in phase. Capacitive loads have a 'leading' phase, where the current waveform occurs first, followed by the voltage. Inductive loads have a 'lagging' phase shift, meaning that the current lags (is behind) the voltage. The seemingly impossible case where the current occurs before the voltage is quite real, but it does take a couple of cycles before the steady state conditions are reached.
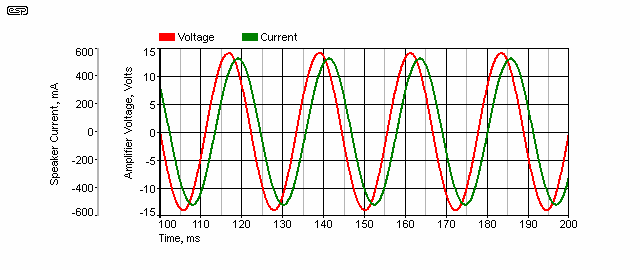
Figure 3 - Phase of Voltage Vs. Current With Reactive Load
As you can see, the voltage comes first, followed by the current (lagging power factor because of inductive load). In this case, the phase angle is 38°, and was taken from the loudspeaker system shown in Figure 1 at a frequency of 45Hz. This is well before resonance, and the impedance is 27 ohms (10V RMS and 371mA RMS). You could be forgiven for imagining that the power into the speaker system is 3.71W (voltage times current), but it's not ...
P = V × I × cos(φ), where φ is the phase angle and 'cos' means cosine. Therefore ...
P = 10 × 0.371 × 0.788 (cosine of 38°) = 2.92W
With a reactive load, some of the power delivered by the amplifier is 'wasted' (in electrical engineering this is called power factor). While the excess current performs no work (such as making sound or heating the voicecoil), it enables work to be performed. It also causes the power amplifier to get hotter than expected, because the 'excess' power is returned to the amplifier and must be dissipated by the power transistors.
For amplifier testing using a 1kHz sinewave, a speaker load can be simulated by placing a 640µH inductor in series with a 4 ohm load resistor. This provides 4 ohms of (inductive) reactance in series with 4 ohms resistance. The combined impedance is 5.66 ohms at 1kHz. While obviously not the same as a loudspeaker load, it is good for testing to ensure that amplifiers don't either fail or trigger protective circuits. The combination is also useful for simulations as it enables accurate determination of the peak transistor dissipation. The phase shift caused by this network is 45° lagging.
It must be understood that the leading and lagging phase conditions are called 'steady state' - the signal has to be present for a period before the voltages and currents achieve their steady state values and relative phases. The actual time needed varies, based on the damping applied to the system and many other factors, but in general, about 2 to 4 cycles will actually be enough. Normal music will easily be able to set up the necessary conditions for the voltage and current to be out of phase with any loudspeaker system. Let's have a look at the phase response of the speaker system shown in Fig 1.
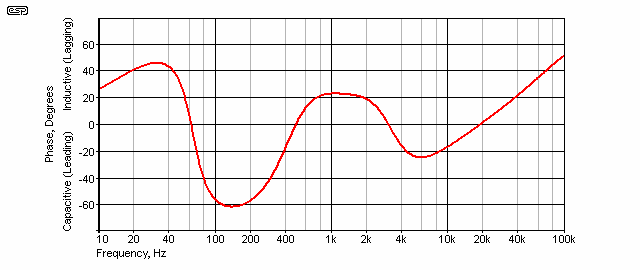
Figure 4 - Phase Response of Simulated Speaker
The phase varies over approximately +45°/ -60°, and while this is fairly realistic, some speakers will exceed this. The majority (and especially mid-woofers as used in most 2-way systems) will have a phase response of ±45 degrees or so, some will be more, others less. It is worth noting just how little of the frequency range appears resistive - the phase angle over the majority of the frequency range is greater than 10° in one direction or the other. The impedance is purely resistive only at the points where the phase angle is zero!
Assume a 100W amplifier and a nominal 8 ohm load. Full power output is reached at a voltage of 40V peak (28.29V RMS). Maximum current is 40 / 8 = 5A peak or a little over 3.53A RMS. This is exactly the voltage and current at full power into a resistive load, and the peak transistor dissipation occurs at 1/2 the supply voltage.
At an instantaneous level 20V into 8 ohms, current is 2.5A, and transistor peak dissipation is 20 × 2.5 = 50W. If voltage and current are out of phase, the power delivered to the load is decreased, and the power dissipated by the transistor is increased.
Worst case (never achieved with any loudspeaker), is a 90 degree phase shift (the cosine of 90° is zero!). This means that when the voltage across the transistors is at the minimum (turned fully on), the current is also at a minimum. That seems pretty good - zero dissipation can't be all bad. The problem is that the converse also applies, so when the voltage across the transistor is at the maximum, so is the current!
Assuming zero losses and an 8 ohm purely reactive load, that means that when the transistor has the full 40V supply across it, it is simultaneously supplying the peak current of 5A. Instantaneous dissipation is therefore 40 × 5 = 200W. Note that it doesn't matter if the reactance is capacitive or inductive, the end result is the same.
So, where it appeared that a 50W transistor was quite adequate, it is obvious that it will fail under these conditions. Add to this the fact that transistors have a SOA (Safe Operating Area) that limits the peak dissipation to the maximum rating or less (depending on voltage and current), and it is easily seen that more powerful transistors must be used.
Now, I stated earlier that the 'worst case' was never achieved in practice, and this is the only thing that saves us. In reality, the voice coil resistance is always in circuit, and this limits the maximum phase angle. Other resistances also help reduce the maximum phase angle - inductor resistance, speaker lead resistance and internal wiring all help to reduce the maximum phase angle.
Looking back to Fig. 1, you can see that the voice coil resistance is not 8 ohms as you might expect, but 6.8 ohms. This resistance is the only factor that stands between your amplifier and a 100% reactive load, and the typical phase angle as a result is typically a little over 45 degrees. The speaker in Fig. 1 has a maximum phase angle of about -60° (capacitive) - not an unrealistic figure.
At 45 degrees, the transistor peak dissipation is doubled, compared to the case with a resistive load. This means that for our 100W 8 ohm amp, the transistor dissipation will be 100W instead of 50W - any increase of phase angle over 45 degrees increases the peak dissipated power vs. the power delivered to the load. It is fair to assume that the 'real life' worst case phase angle will be around 60 degrees, and will occur only near (above or below) resonance, or around the crossover frequency. Note that when the phase angle is 45°, the power delivered to the loudspeaker is half that you may calculate using voltage and current. Remember ...
P = V × I × cos(φ) (where φ is the phase angle)
Table 1 shows the relationship between phase angle (the difference between voltage and current, measured in degrees), peak power dissipated in the amplifier and average power delivered to the load, normalised to 1W. The type of amplifier is unimportant - transistors, MOSFETs (lateral or vertical), valves or 'magic' - all are affected equally. (Note that 'magic' amplifiers do not exist, other than in the minds of some people or in some colour glossies.)
Note that peak power is not the average power - these are entirely different things. Average power is used to determine the heatsink requirements, but peak power is the killer of bipolar junction transistors (BJTs) due to second breakdown. Lateral MOSFETs and valves will survive these momentary peaks without complaint - BJTs will not!
The following table is for peak dissipation at the onset of clipping, and the situation is very different at worst case output level (¼ the maximum power, or ½ total voltage swing). Note that the values are 'normalised' (i.e. referenced to unity), and are not determined by the power factor. The values shown are the result of multiple calculations that have been normalised in order to show clearly the effective power distribution between the amplifier and the load.
For example, with a phase displacement of 45°, the amplifier has a peak dissipation that's exactly double that when driving a resistive load. The reactive load that causes a 45° phase shift dissipates a peak power that's exactly half that of a resistive load for the same amp output voltage. These results can be simulated, but are not particularly easy to calculate unless you are willing to use complex maths (i.e. calculating the 'real' and 'imaginary' parts of the load voltage and current, due to reactance).
The figures shown below are not exact because they don't need to be. Normal music will have the amplitude, frequency and phase shift in constant movement, so we need to understand trends rather than absolute values.
| Phase Angle | Power Factor - cos(φ) | Peak Power (Amp) | Peak Power (Load) |
| 0° | 1.000 | 1 | 1 |
| 15° | 0.966 | 1.38 | 0.94 |
| 30° | 0.866 | 1.76 | 0.75 |
| 45° | 0.707 | 2 | 0.5 |
| 60° | 0.500 | 1.66 | 0.24 |
| 75° | 0.259 | 1.2 | 0.08 |
| 90° | 0.00 | 4 | 0 |
Power Factor (cos(φ)) has been included, not so much because it is something you specifically need to know, but because some knowledge of it is likely to be useful. Power factor is determined by taking the cosine of the phase angle, and is essentially a 'figure of merit' for an AC load. This was shown in the formula above, where cos(φ) is the cosine of the phase angle.
The 'magic' figure of 45° is worst case with typical systems, where the transistors must dissipate double the normal peak power, while the load only receives half the power it would normally get. Note that the amplifier peak dissipation appears to fall after 45 degrees - this is only because of the increased impedance presented because of the reactance. While these figures are reasonably accurate, it must be understood that the situation varies depending on output power and supply voltage - there are a great many variables, and it is not practical to try to cover them all.
The load power is interesting. Notice that at 90 degrees, there is zero power delivered to the load! There is voltage and current (referred to as VA with transformers), but no power, so no physical work is done - the speaker would be silent. This phenomenon is well known in the power industry, and is called power factor. The ideal case is a power factor of 1, where every volt and amp is converted into work - heat, light or rotation (for example).
Obviously, the worst case is a power factor of zero. Volts and amps are readily measured, yet no work is done, and the electricity meter remains still. The majority of real loads are somewhere in between, and the loudspeaker is no exception. A speaker load will always have a 'real' component in the equation - the voicecoil resistance - so a power factor of zero is not possible. It is beyond the scope or intent of this article to discuss this further, so I won't.
The essential to understand is that any power amplifier must have sufficient reserve power dissipation in the output (and driver) transistors to handle the maximum possible peak thermal loading. In real terms, this always means more (or larger) output devices than you anticipated.
As an example, we can look at an 8 ohm load, with 8 ohms of inductive reactance in series. Despite how this may appear, the effective impedance is not 16 ohms, it's really 11.3 ohms (8 × √2). You will often see this written as 8+j8 ohms, where the 'j' indicates a reactive (aka 'imaginary') value. With an output voltage of 28V RMS (±42V supplies), the current drawn is 2.42A. The apparent power (volt-amps) delivered to the loudspeaker is 70VA, and because the power factor is 0.7, the real power is 50W. This is all very confusing, but it's perfectly real, and obeys the laws of physics in all respects.
Meanwhile, the power transistors have an average dissipation of about 22W each, but the peak dissipation is 100W. If the load were resistive (8 ohms), the peak dissipation would only be 54W and the average power is 17.5W - a significant difference! This is explored in greater detail in the next section, except a 4 ohm load will be assumed as this is more representative of many speaker systems.
Let's assume that we want 100W into 4 ohms, based on the design of P3A. That means 20V RMS, or 28.2V peak. Assuming no losses, we shall use a power supply of ±35V. Peak output transistor dissipation at 106W into a 4Ω resistive load is 70W, at an average of just over 20W (each transistor - 46W for the pair). This represents an easy load for the amp, and could easily lull one into a false sense of security. Note that the power of 106W is based on the supply voltage remaining steady at ±35V, but in reality it will fall as power output is increased. 100W is realistic with a typical power supply.
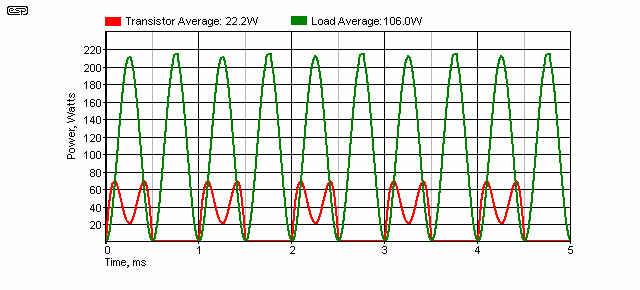
Figure 5 - Power With Resistive Load
Worst case power dissipation (resistive) is actually at around 0.707 of the maximum output voltage (½ power), or 14V RMS. Peak transistor dissipation is still 70W, but the average power increases to a little over 28W because of the way amplifiers work (this topic is covered in greater depth in the Amplifier Design article). This is not a large increase, but every Watt that needs to be disposed of means a greater load on the heatsink.
It is not unreasonable to design for a worst case phase angle of 45°, and as shown in the table above, power actually falls slightly above this. At 45° the peak dissipation is as shown in Figure 6 - this is where things can go pear-shaped in a hurry if you underestimate the operating conditions of a real-world amplifier. Transistor dissipation just before clipping is a bit over 124W (with an average of 28W). Any increase of the supply voltage will push the repetitive peak dissipation into the danger zone - especially when the power transistors are at an elevated temperature.
The above is based on a ±35V supply, but if you increase this to ±42V, at 4 Ohms reactive the peak dissipation will be over 200W ... the maximum rating for the transistors ... at 25°C!. Since it is highly unlikely (impossible, more like it) that the transistor die will be maintained at 25°C, the device must also be derated accordingly. Therefore, P3A cannot be used safely into 4 Ohms with a ±42V supply (something I have been claiming all along  ).
).
The bottom line is that to deliver 100W safely into 8 ohms, and allow 4 ohm operation, you need 400W of available transistor dissipation to ensure that the transistor SOA will not be exceeded at any time. In most amps, that means two pairs of output transistors are needed, although it's very common to see designs that use only one pair. This is always a risk, and while you might get away with it, at some point it will come back to bite you.
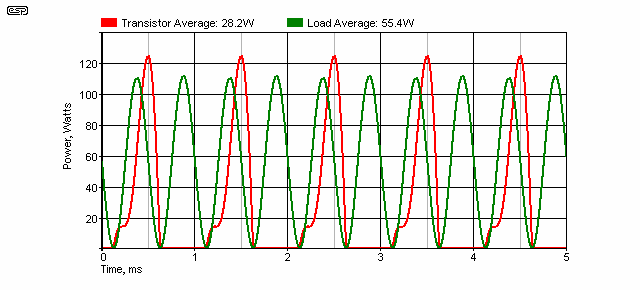
Figure 6 - Power With Reactive Load
Now you know why P3A (for example) is designed for operation at ±35V, and the suggested upper limit (8 Ohms only) is ±42V. When losses are taken into consideration, this is the absolute maximum recommended operating voltage. Under these conditions, using 200W output transistors, it is perfectly fine if the recommended supply is used, but is at risk if you go for the upper limit. The amp might be saved from destruction into 4 ohms (at the maximum voltage) by the fact that the supply voltage will collapse, and although this is common feature with many amplifiers, it is not recommended. Alternatively, you can always try your luck - it is amazing just what some people have managed to get away with, but this is not an approach that I am comfortable with.
You may have noticed that the figures shown here are somewhat conservative. Many devices can tolerate higher than rated power dissipation for short periods, and the SOA (safe operating area) graphs often show instantaneous peak dissipation for 1 second, 100ms and 10ms that are far higher than the continuous (DC) maximum. It's not always clear that these figures are for a die (junction) temperature of 25°C, and that they must be derated at higher temperatures. No power amplifier that's turned on will ever maintain the die temperature at 25°C, because there is always some quiescent current, and when the amp is being driven the temperature will be higher. The actual operating temperature depends on the output level and the load, and can be calculated by careful examination of the heatsink and transistor mounting. This is covered in detail in the Heatsinks article.
It is quite obvious that the heatsink is of paramount importance, as is the transistor mounting. Maintaining the lowest possible thermal resistance keeps the transistors cool, and limits the amount of derating that must be applied. Other techniques that may be used include protection circuits, but these must also take the maximum operating temperature into account to be effective. It is widely believed that protection circuits contribute additional distortion and are 'audible', even when not activated. While this is possible with some designs, there is no doubt that aggressive protection most certainly is audible, as evidenced by many IC power amps - these must be kept below the protection threshold at all times.
Class-D (switching) amplifiers show their displeasure by very different means. Because the output devices are switched at a high frequency, the phase angle of the load does not increase dissipation to any marked degree. Instead, they suffer from a phenomenon called 'bus-pumping'. When driving a reactive load, that almost invariably means bass, because that's where the speaker impedance has a significant capacitive or inductive component. As shown above, this causes energy to be sent back to the amplifier. A linear amp disposes of the 'returned' energy as heat in the output transistors. This doesn't happen with Class-D amps, or any of their 'derivatives' such as 'Class-T'.
So, rather than dissipating the energy as heat, it's returned to the supply rails, forcing the voltage to rise. This is a phenomenon called bus-pumping, because it 'pumps' the supply buses (rails) to a higher than normal voltage. Two things can happen, either ...
a) The amp's over-voltage detector operates and the amplifier shuts down until the voltage is back within spec.
b) The amplifier blows up.
There are a couple of ways this can be mitigated. Using Class-D amps in full bridge mode (two amps with opposite phase, aka BTL) means that while one side attempts to push the supply rail higher, the other is delivering current, so the effects cancel. For single amps, it's common to have one with the signal inverted (so the red output terminal is 'cold' and the black terminal is 'hot'). Bass is generally pretty close to being mono in most sound mixes, so this works with a full range signal.
Another way around the problem is to use much larger supply filter capacitors than may have seemed necessary. These take longer to charge, so there is less chance that the supply voltage will be pushed higher than the amp can handle.
Bus pumping is not really part of this article, but it's been added because Class-D is gaining in popularity as performance improves, and the effect itself is created by the same issues that linear amps have to deal with. Many will have noticed that a great many Class-D amps are operated in BTL, even when there may seem to be no requirement to do so. The reason is to prevent bus pumping, which can be a major problem with high power amps that are common today.
While this article has taken a somewhat simplistic approach to the issue, it is a reasonable description of reality. Real loudspeakers in enclosures will invariably make the amplifier's job harder than any resistive load, and even more so with a vented box. Few loudspeakers will present anything that looks even remotely like a resistive load, so amplifier dissipation will always be worse than simple analysis would indicate.
Of enclosures, the transmission line will usually present the easiest load to an amplifier, but unfortunately these are much larger than a conventional sealed or vented box. In all cases, a passive crossover network will also present additional phase shift. In some cases this can be extreme (usually due to poor design IMO).
At high frequencies, the amplitude is much lower than at low and mid frequencies, and even quite radical phase shifts do not cause undue amplifier stress.
The thing that saves some amplifiers is the power supply impedance, and careful design (hint - the cheapest alternative) ensures that there is enough power available for transients, but it will collapse sufficiently to allow for worst case conditions. This is not a good method to rely on, but if you are prepared to perform extensive testing you'll be able to get more 'transient' power, at the expense of steady state power. The typical range is 1.5 to 2dB with most commercial designs.
Some commercial amplifiers use a tapped power transformer, and have settings for 8 and 4 ohms. The voltage is reduced for 4 ohm operation to make sure that the transistor SOA is not exceeded. Others take a more simplistic approach (many subwoofer amps fall into this category), where the transformer is simply too small for the job. If loaded heavily and driven hard, the supply voltage will collapse because of the under-rated transformer, and the amp will survive. Fortunately, music is dynamic, so the transformer will not have to suffer a sustained overload, and will usually live a long and happy life.
Remember, see the Safe Operating Area article for more detail on this topic.
All graphs shown were captured from SIMetrix circuit simulation software.
 Main Index
Main Index
 Articles Index
Articles Index