

|
| Elliott Sound Products | Satellites and Subwoofers |
 Main Index
Main Index
 Articles Index
Articles IndexIn recent years the satellite sub woofer type of loudspeaker system has become popular, this largely due to the advent of surround sound home theatre. For this and also for music the sat+sub system has many things to recommend it, the use of one subwoofer is made possible because the range bellow 100Hz is, as indicated by most testing, non directional, thus allowing the subwoofer to be put in the best place for bass, and allowing the various other smaller speakers to be arranged in a way most suited to imaging and surround effect. Another benefit is that the higher cut off frequency of the satellites potentially keeps the non linear distortion caused by large low bass cone excursions at a low level.
The low cost and compact size is however bought at a cost, this is that the sound pressure generated by such a system is limited by the use of a small driver down to a typical 80Hz crossover frequency. This is exacerbated by the current fashion to denigrate the reflex enclosure, with people advised to block up those despised ports, and be transported to the sunlit uplands of sonic bliss thereby.
It is generally true that the transient response of vented enclosures is not as good as that from a (properly designed) sealed box, but we live in a world of compromise. There is little point having a system with perfect transient response if the distortion at realistic listening levels is intolerable. It is also pointless to try to convince someone who has a small listening area that they need large 3-way systems - especially if there is no physical room for such enclosures. So, in this area of compromise, there has to be a solution that will provide a reasonable SPL with minimal excursion created distortion.
While sealed enclosures certainly have their place in the scheme of things, any attempt to use them in a 'full range' 2-way system will almost certainly cause excessive distortion at even a moderate SPL, whereas a solution is available that lowers distortion, raises the SPL limit and if carefully done will give very good performance.
Interestingly, any information about the alignment discussed in this article is very scarce on the Net, to the extent that it is almost non-existent. While the author has recommended the method described for some time (mainly in forum sites), it is an alignment that the editor has also contemplated, but (until now) did not have the information to perform a theoretical design - any attempts had to be empirical. That this is time consuming in the extreme is obvious, and it is probable that the Quasi-Butterworth, 5th order (QB5) alignment will see an increase in popularity in the future.
What follows is a discussion of the issues and methods for dealing with the most vexing problems, but first some discussion about the linear excursion limit is in order.
Over part of its cone excursion the loudspeaker driver is to a good approximation a linear transducer, if its B×L (magnetic field strength × conductor length) product is constant, then the force generated by the voice coil is linearly proportional to the current in the voice coil, i.e. ...
F = ( B × L ) × I
Olsen, in his 1962 paper [1], identified two non linear elements that produce harmonic distortion as a function of cone displacement. Typically as the voice coil moves out of the magnetic gap, the B×L product is no longer constant but starts to fall as the excursion increases, this can be described mathematically as ...
F(x) = a × x + bx² and F(x) = a × x + bx³
Where, F(x) is an expression relevant for force when B×L is falling, a & b are constants relevant to a particular driver, and x is the displacement. The first of these expressions is relevant for the voice coil moving from its rest position asymmetrically, and the second when the motion is symmetrical about the centre position.
When excited by a sine wave the Fourier transform of these yields ...
x = A × cos ωt + B× cos 2ωt and x = A ×cos ωt + B× cos 3ωt
Where ω represents the angular frequency (equal to 2πf), x is the amplitude, ωt is the exciting frequency and A ,B are proportional constants, dependant upon signal level.
The second terms, B × cos 2ωt and B × cos 3ωt represent the second and third harmonics respectively.
For small displacements when BL is constant, the second term is vanishingly small, and the distortion produced comes from non linearities in the suspension and surround, and from air trapped in the magnetic gap. The 2nd harmonic component is largely out of our control since its level is largely due to the design and construction of the driver.
The third harmonic is in our control however because it is directly related to the amount of signal we put in. This where the linear excursion comes in....
The peak linear excursion limit is derived, unless it is specified by the manufacturer, by using the rule of thumb that it is the voice coil length, minus the magnetic gap height over two, this is true for the usual overhung voice coil. Gander, [2] measured a wide selection of drivers and came up with the findings that calculating the linear excursion limit in this way is a very reliable indicator of the driver producing 3% third harmonic distortion, when driven to this limit. In what follows this is taken as the maximum peak distortion that is acceptable.
As an example of what this means in practical terms, let us take a typical good quality satellite mid/woofer, the Vifa P17WJ, and put it in a sealed box.
| Nominal impedance [ohm] | 8 | Air gap height [mm] | 6 |
| Voice coil resistance [ohm] | 5.8 | Voice coil inductance [mH] | 0.55 |
| Nominal power [W] | 40 | Eff. diaphragm Area [cm²] | 136 |
| Short term max power [W] | 350 | Moving mass [g] | 14 |
| Long term max power [W] | 150 | Magnet weight [g] | 415 |
| Operating power [W] | 6.3 | Force factor [Bl] | 6.5 |
| Sensitivity [dB] | 88 | VAS [litres] | 34.7 |
| Frequency range [Hz] | 37-5000 | Qms | 1.55 |
| Free air resonance [Hz] | 37 | Qes | 0.45 |
| Voice coil diameter [mm] | 32 | Qts | 0.35 |
| Voice coil height [mm] | 14 |
In a box of 11.5 litres it will have a Q of 0.707 and an fs around 78Hz by the manufacturers specifications. it has a linear cone excursion of around 4mm peak. Using Small's expression for the acoustic power we can expect in an average room [3]
Pa = kp × Vd2 × f34
Where kp is the power output constant, it has a value of around 0.8 for a sealed box
Vd is the volume displacement (cone area × peak excursion) and f3 is the system's lower -3dB frequency. This gives...
kp = 0.8 × (0.0136 × 0.004)2 × 784 = 0.088 WattsConverting this to decibels we have...
107.5 - 10 × log10 (1 / 0.088) = 96.9dB
This is the peak sound level we can reproduce before exceeding the excursion limit. Taking into account that "normal" program is said to have a 20dB dynamic range then our average level is around 77dB. This falls far short of the standard 90dB with 20dB headroom requirement for a hi fi system. Although it can play a lot louder, this will not be without producing large amounts of harsh sounding non linear distortion - the amount of distortion increases very rapidly beyond our excursion limit.
For instance the 110dB peak output causes a 4mm excursion at 189Hz. At the 78Hz region, the driver needs an excursion of 16mm.
From the above it seems that the position is hopeless, crossing small satellites of this sort over to a single subwoofer causes large amounts of distortion.
There are of course several alternatives, these include three way satellites, stereo subwoofers crossing over at a higher frequency and so on, but all of these lack the basic simplicity and low cost of the two way satellite plus single subwoofer system.
Luckily there is a solution, this is in the form of the QB5 reflex alignment.
I know that immediately I say that word 'reflex', many people will throw their hands up in horror, make the sign of the cross, or other gestures that are best not considered. Swimming against the tide of fashionable anti-reflex sentiment is difficult, but I nevertheless present the following for your consideration ...
Two people named Kreutz and Panzer derived the QB5 reflex alignments, and published their work in 1993, [4] the class II group of these have the characteristic that they optimise power handling by means of reducing the cone excursion needed for a given acoustic power output, and these are the most useful for our purpose.
In essence, what we will do is create a box that is specifically designed to have a peaked response at the low end. This means that the box tuning (rather than the loudspeaker cone) is producing the larger proportion of the LF energy, so less power is needed to achieve a given SPL. In order to prevent the system sounding like a boom-box, a 2nd order filter (whose Q is also obtained from the table) is placed before the power amp, tuned to the frequency obtained from the charts below. The system as a whole will now have a vastly higher power output at the low frequency end, without the problem of excursion limiting and subsequent distortion. On the down side (and like all things, there are compromises), the box will be larger than a conventionally tuned system, but this would be the case regardless if a larger woofer were to be used to try to maximise the excursion limited SPL.
The details of these derivations are as they say 'beyond the scope of this article', and for those interested the paper cited in the references is available from the AES. Suffice to say however, that the benefits of filter assisted reflex boxes have been known and exploited for many years, but the derivation of these particular alignments was not achieved formally until Panzer came up with a solution to some very difficult mathematics. Luckily for us this gave us three alignment tables, these are reproduced below.
[Reproduced from:- "Derivation of the Quasi-Butterworth 5 Alignments" , by J.J.M. Kreutz & J. Panzer, Journal of the Audio engineering Society, Vol. 42, No. 5, May 1994]
| Qt | Vas/Vb | F3/Fs | kp | Fb/Fs | 1/Qa | T60 | Fa/Fs |
| Driver Qts | Box Volume | -3dB Freq. | Power Ratio | Box Tuning | Filter Damping | Settling Time | Filter Freq. |
The three tables stem from the value of a parameter used in the solutions of the equation set. In practical terms, Group I is the optimum power handling vs. bass extension for drivers in the Qt range specified. The Group II alignments are for maximum power handling, again within the Qt range covered. Group III are included for completeness, as they represent the edge of usefulness and can be largely ignored.
| Qt | Vas/Vb | F3/Fs | kp | Fb/Fs | 1/Qa | T60 | Fa/Fs |
| 0.324 | 1.989 | 0.935 | 3.911 | 0.995 | 0.467 | 4.778 | 0.944 |
| 0.318 | 2.103 | 1.000 | 6.436 | 1.00 | 0.518 | 4.315 | 1.000 |
| 0.311 | 2.239 | 1.059 | 6.782 | 1.008 | 0.549 | 4.074 | 1.055 |
| 0.303 | 2.396 | 1.114 | 7.237 | 1.018 | 0.569 | 3.933 | 1.110 |
| 0.295 | 2.574 | 1.169 | 7.811 | 1.030 | 0.582 | 3.844 | 1.164 |
| 0.287 | 2.773 | 1.223 | 8.512 | 1.046 | 0.592 | 3.785 | 1.219 |
| 0.279 | 2.991 | 1.277 | 9.349 | 1.063 | 0.598 | 3.746 | 1.274 |
| 0.271 | 3.229 | 1.332 | 10.331 | 1.083 | 0.603 | 3.717 | 1.329 |
| 0.263 | 3.486 | 1.387 | 11.469 | 1.104 | 0.606 | 3.697 | 1.385 |
| 0.255 | 3.762 | 1.443 | 12.776 | 1.127 | 0.608 | 3.682 | 1.441 |
| 0.247 | 4.056 | 1.499 | 14.265 | 1.152 | 0.610 | 3.671 | 1.498 |
| 0.240 | 4.368 | 1.556 | 15.951 | 1.178 | 0.612 | 3.663 | 1.555 |
| 0.233 | 4.698 | 1.614 | 17.849 | 1.205 | 0.613 | 3.656 | 1.613 |
| 0.226 | 5.046 | 1.672 | 19.977 | 1.234 | 0.614 | 3.651 | 1.671 |
| 0.219 | 5.412 | 1.731 | 22.352 | 1.263 | 0.614 | 3.647 | 1.730 |
| 0.213 | 5.795 | 1.790 | 24.992 | 1.293 | 0.615 | 3.643 | 1.789 |
| 0.207 | 6.196 | 1.849 | 27.919 | 1.324 | 0.616 | 3.641 | 1.848 |
| 0.201 | 6.614 | 1.909 | 31.153 | 1.356 | 0.616 | 3.639 | 1.908 |
| 0.196 | 7.050 | 1.969 | 34.716 | 1.389 | 0.616 | 3.637 | 1.968 |
| 0.190 | 7.503 | 2.030 | 38.631 | 1.422 | 0.616 | 3.635 | 2.029 |
| 0.185 | 7.973 | 2.090 | 42.921 | 1.456 | 0.617 | 3.634 | 2.090 |
| Qt | Vas/Vb | F3/Fs | kp | Fb/Fs | 1/Qa | T60 | Fa/Fs |
| 0.445 | 0.550 | 1.000 | 6.436 | 1.000 | 1.414 | 4.316 | 1.000 |
| 0.425 | 0.751 | 1.152 | 10.152 | 1.115 | 1.527 | 3.919 | 1.107 |
| 0.415 | 0.856 | 1.231 | 12.587 | 1.174 | 1.558 | 3.839 | 1.187 |
| 0.405 | 0.960 | 1.303 | 15.176 | 1.228 | 1.576 | 3.790 | 1.264 |
| 0.394 | 1.072 | 1.373 | 18.090 | 1.281 | 1.588 | 3.756 | 1.339 |
| 0.384 | 1.193 | 1.444 | 21.426 | 1.335 | 1.595 | 3.729 | 1.415 |
| 0.373 | 1.325 | 1.515 | 25.264 | 1.389 | 1.601 | 3.709 | 1.491 |
| 0.362 | 1.467 | 1.588 | 29.678 | 1.444 | 1.604 | 3.693 | 1.567 |
| 0.352 | 1.620 | 1.661 | 34.742 | 1.500 | 1.607 | 3.681 | 1.643 |
| 0.342 | 1.784 | 1.736 | 40.528 | 1.557 | 1.609 | 3.671 | 1.720 |
| 0.331 | 1.959 | 1.811 | 47.115 | 1.615 | 1.611 | 3.663 | 1.797 |
| 0.322 | 2.144 | 1.887 | 54.580 | 1.674 | 1.612 | 3.657 | 1.875 |
| 0.312 | 2.339 | 1.963 | 63.009 | 1.733 | 1.613 | 3.652 | 1.953 |
| 0.303 | 2.545 | 2.040 | 72.486 | 1.793 | 1.614 | 3.648 | 2.031 |
| 0.294 | 2.761 | 2.118 | 83.102 | 1.854 | 1.615 | 3.645 | 2.110 |
| 0.286 | 2.988 | 2.196 | 94.952 | 1.916 | 1.615 | 3.642 | 2.188 |
| 0.278 | 3.224 | 2.274 | 108.134 | 1.978 | 1.616 | 3.640 | 2.268 |
| 0.270 | 3.470 | 2.353 | 122.749 | 2.04 | 1.616 | 3.638 | 2.347 |
| 0.262 | 3.726 | 2.432 | 138.903 | 2.103 | 1.616 | 3.636 | 2.426 |
| 0.255 | 3.993 | 2.511 | 156.706 | 2.166 | 1.616 | 3.635 | 2.506 |
| 0.249 | 4.269 | 2.590 | 176.216 | 2.229 | 1.617 | 3.634 | 2.586 |
| Qt | Vas/Vb | F3/Fs | kp | Fb/Fs | 1/Qa | T60 | Fa/Fs |
| 0.514 | 0.533 | 1.029 | 4.976 | 1.018 | 2.020 | 3.833 | 0.794 |
| 0.517 | 0.527 | 1.030 | 5.136 | 1.019 | 2.008 | 3.852 | 0.813 |
| 0.520 | 0.520 | 1.031 | 5.295 | 1.02 | 1.996 | 3.871 | 0.832 |
| 0.523 | 0.513 | 1.032 | 5.451 | 1.02 | 1.987 | 3.892 | 0.850 |
| 0.526 | 0.505 | 1.032 | 5.603 | 1.020 | 1.978 | 3.914 | 0.867 |
| 0.530 | 0.496 | 1.032 | 5.749 | 1.020 | 1.970 | 3.939 | 0.884 |
| 0.534 | 0.487 | 1.031 | 5.887 | 1.020 | 1.963 | 3.966 | 0.901 |
| 0.538 | 0.476 | 1.030 | 6.016 | 1.019 | 1.957 | 3.997 | 0.917 |
| 0.543 | 0.465 | 1.028 | 6.133 | 1.017 | 1.951 | 4.031 | 0.932 |
| 0.549 | 0.452 | 1.024 | 6.234 | 1.015 | 1.947 | 4.070 | 0.947 |
| 0.555 | 0.438 | 1.020 | 6.319 | 1.013 | 1.942 | 4.116 | 0.961 |
| 0.562 | 0.422 | 1.015 | 6.383 | 1.009 | 1.938 | 4.171 | 0.975 |
| 0.569 | 0.405 | 1.008 | 6.423 | 1.005 | 1.935 | 4.236 | 0.988 |
| 0.577 | 0.386 | 1.000 | 6.434 | 1.000 | 1.932 | 4.317 | 1.000 |
| 0.587 | 0.364 | 0.990 | 6.251 | 0.994 | 1.929 | 4.417 | 1.011 |
| 0.598 | 0.339 | 0.977 | 6.035 | 0.986 | 1.927 | 4.545 | 1.022 |
| 0.610 | 0.312 | 0.962 | 5.780 | 0.977 | 1.924 | 4.713 | 1.031 |
| 0.625 | 0.280 | 0.943 | 5.482 | 0.966 | 1.922 | 4.939 | 1.039 |
| 0.643 | 0.244 | 0.921 | 5.132 | 0.952 | 1.921 | 5.254 | 1.045 |
| 0.664 | 0.202 | 0.894 | 4.719 | 0.936 | 1.919 | 5.716 | 1.049 |
| 0.691 | 0.150 | 0.861 | 4.224 | 0.915 | 1.918 | 6.449 | 1.050 |
* T60 is the time needed for a pulse input to settle by 60dB
Plugging our Vifa P17WJ driver into the relevant class II alignment, i.e. that for a Qt of 0.35, yields (after calculation) the following ...
| Box volume | 21.4 litres |
| f3 | 61.5Hz |
| Box tuning frequency | 55.5 Hz |
| Fa (Aux. filter 12dB/Octave high pass) | 60.8Hz |
| Qa | 0.622 |
| kp | 34.74 |
Note that in the above the power handling constant kp has gone up from 0.8 to an impressive 34.74, the practical effect of this is shown below...
Pa = 34.74 × (0.0136 × 0.004)2 × 61.54 = 1.47 Watts
dB SPL = 10 × log10(1.47) + 107.5 = 109.17dB
Our peak output before we reach our excursion limit has gone up by 12.3dB even with a lower f3, if we use the high pass filter from our subwoofer amplifier this should be set at the 61Hz frequency as a minimum, setting it higher results in an even greater increase in power handling.
Two of these speakers in a room can easily meet the 110dB SPL peak level that is the standard for domestic hi fi systems without exceeding the 4mm peak cone excursion limit, this results in a significant reduction in non linear distortion. One must be careful not to exceed the long term power handling of the drivers - since there will be little loudspeaker distortion at even high levels, there will be no warning that the average electrical power is too high, so some common sense is required to prevent voicecoil damage.
Another fully worked example (similar speaker, but different parameters) will help understanding ...
| Nominal impedance [ohm] | 6 | Air gap height [mm] | - |
| Voice coil resistance [ohm] | 4.0 | Voice coil inductance [mH] | 0.4 |
| Nominal power [W] | 50 | Eff. diaphragm Area [cm²] | 140 |
| Short term max power [W] | - | Moving mass [g] | - |
| Long term max power [W] | - | Magnet weight [g] | - |
| Operating power [W] | - | Force factor [Bl] | 4.1 |
| Sensitivity [dB] | 87 | VAS [litres] | 49.4 |
| Frequency range [Hz] | - | Qms | 1.34 |
| Free air resonance [Hz] | 35 | Qes | 0.58 |
| Voice coil diameter [mm] | - | Qts | 0.40 |
| Voice coil height [mm] | - |
The above data were obtained from WinISD, and some parameters are missing, or may be in error. However, this was used for the simulations that follow, and the general idea is the same for any speaker.
| Driver | Vifa P17WG-00-08 | ||
| Qt | 0.40 | ||
| fs | 35 Hz | ||
| Vas / Vb | 0.960 | Vb = 49.4 / 0.96 | Vb = 51.45 litres |
| f3 / fs | 1.303 | f3 = 35 × 1.303 | f3 = 45.6 Hz |
| fb / fs | 1.228 | fb = 35 × 1.228 | fb = 42.98 Hz |
| 1 / Qa | 1.576 | Qa = 1 / 1.576 | Qa = 0.635 |
| fa / fs | 1.264 | fa = 35 × 1.264 | fa = 44.24 Hz |
The box in this case is a little over the normal volume for a critically aligned vented enclosure, and will have a response as shown below. The normal reaction to this would be "Yuck!" because of the large peak of 2.45dB occurring just before rolloff. This is where the electrical filter comes into play, and this filter should have a frequency of 44.24 Hz (fa) and a Q of 0.635 (Qa) to match this alignment.
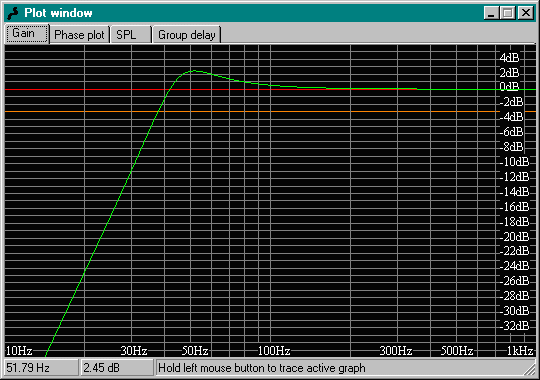
Figure 1 - Speaker Response
The above graph is the output from WinISD, with the box size and tuning frequencies adjusted according to the calculations above. The actual f3 point of the speaker is 37.8Hz, but this will be raised by the electrical filter to the figure of 45.6Hz as obtained from the table. The simplest filter to use for this is the equal component value Sallen-Key, and the schematic for this is shown below. As noted above, the exact Q will not make a great deal of difference - it may look bad, but will be completely overshadowed by room nodes. For the time being, we'll look at the system response with the correct Q, especially since it is quite easy to do.
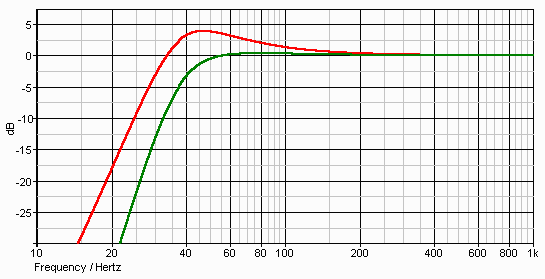
Figure 2 - Speaker (Red) and Combined (Green) Response
I used the Simetrix simulator to produce the above, and although it is not a perfect match for the loudspeaker response in Fig. 1, the result is very close. The red trace is the uncorrected simulated loudspeaker response, while the green trace shows the result after correction with the auxiliary filter. The simplest way to make the auxiliary filter is to use the 'equal component value Sallen-Key' filter topology. This allows independent selection of frequency and Q, but the gain of the circuit will change. The gain obtained from a low Q filter is small, and is unlikely to cause any problems in typical systems.
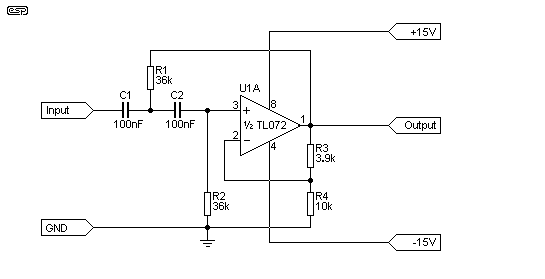
Figure 3 - Auxiliary Correction Filter Circuit
Referring to the schematic above, you can see that R1=R2 and C1=C2. The second half of the opamp would be used for the other channel. Note that this circuit must be fed from a low impedance source (typically less than 1k). The values needed are given by ...
f = 1 / (2π × R × C)
This is not affected by the gain setting (which alters the Q), so it is a flexible solution with no bad habits. For the filter response we calculated above, first we shall select a convenient value for C - say 100nF. The value for R is obtained by ...
R = 1 / (2π × C × f ) = 1 / ( 2π × 100E-9 × 44.24 ) = 35.98kΩ
It has to be said that the calculated resistance value is not going to be easy to get, but a 50k dual-gang pot will allow you to set the frequency wherever you like. Alternatively, you could use a 33k and a 2.7k in series, or even just 33k with a still insignificant error. Now that the frequency is decided, we need to calculate the Q. This is not even a little bit painful, since the tables actually give the figure for damping (1/Qa), which simplifies things even more.
Q = 1 / (3 - K) or R3 = (2 - d) × R4
where K is the circuit gain (determined by the ratio of R3:R4), and d = 1/Q. For minimum DC offset, the parallel combination of R3 and R4 should equal R1, but this is of no consequence if the power amplifier has a capacitor input as offset will be very low. A value of 10k will be quite acceptable for our purposes. From the table, we determined that d (1/Qa) is 1.576, so substituting ...
R3 = (2 - 1.576) × 10k = 0.424 × 10k = 4.24k
Alas, we have another non-standard value, but a 3.9k resistor in series with 330Ω gives 4.23k which will be quite acceptable. In fact, you could just use the 3.9k resistor, since the error is very small indeed, and will be completely un-noticed in practice. The values calculated and shown on the schematic were used in the simulation, and as is obvious, the error is small.
Using the same formula as before, we can calculate the acoustic power increase over a sealed box. 5mm linear excursion is assumed, from the specifications for the P17WG ...
Pa = kp × Vd2 × f34 Pa = 0.8 × (0.0136 × 0.005)2 × 624 = 34mW
and for the QB5 alignment we calculated ...
Pa = 15.176 × (0.0136 × 0.005)2 × 404 = 179mW
Not quite as impressive as the previous example, but note that we have a -3dB frequency of 40Hz instead of 62Hz, and still have a 7.2dB increase in effective acoustic power output. Converting to dB SPL, we get ...
dB SPL = 10 × log10(0.179) + 107.5 = 100.03 dB
The is a substantial improvement over the 92.8dB SPL obtainable from a sealed box, plus we have over ½ octave more low frequency extension. As before, if we were to raise the crossover frequency, there will be an equivalent increase in level before the excursion limit is reached. As it stands, the arrangement just calculated would outperform the majority of systems using conventional vented boxes and the same driver. The enclosure is only marginally larger than a 'critically aligned' system, but has an f3 of 40Hz rather than 34Hz. Another plus is that there is a filter that will help reduce infrasonic excursions that produce no useful output, but can introduce considerable distortion because the cone is unloaded below the cutoff frequency.
As previously mentioned, the 2nd order high pass output from your sub amplifier can be used as the filter. While it is true that this is usually a Butterworth type, with a Q of around 0.7, overall this does not make much difference at this low crossover frequency, as room modes and cancellation/reinforcement from walls predominate over any exact crossover characteristic. Be aware that many 'plate' sub amps have a fixed high-pass filter, and only the low-pass section is variable. Such units will almost certainly need the filter circuit described.
If the high-pass section of the crossover is variable this is also useful, as this allows an optimum setting for a smooth response to be found more easily. It also increases power handling even more. Referring to the original driver (the P17WJ), if kp remains the same and f3 is increased to 80Hz, the excursion limited peak output goes up to 113.7dB - this represents an increase of 16.8dB in peak output over a sealed box before excursion limit is reached. One can use a peak input of 263 Watts in the case of the P17WJ, which has an unspecified 'short term' maximum power input rating of 350 Watts.
The method outlined here allows the maximum performance to be extracted from the single subwoofer plus two way satellite configuration, and in terms of 'bang for your buck' is hard to beat.
It does however use the now demonised reflex enclosure, but it must be emphasised that any negative effects from a port are more than compensated for by the very significant reduction in non linear distortion this technique confers.
In addition, it could be argued that the electrical filter brings the box back into alignment, and not only relieves the loudspeaker of undue stress and distortion, but by removing the low frequency component from the amplifier, the power actually needed could be reduced by perhaps 3dB or more. While this may not sound like much, it is the difference between a 100W amp and a 50W amp, so the savings all round could be very significant.
Curve fit solutions for the first two alignments are presented here. These may be used to calculate the values, rather than using the lookup tables.
Class I Alignments
All of these have a correlation coefficient of at least 0.98, except for 1/Qa, with 0.91
Vas / Vb = 0.126 × (Qt^-2.4731)
F3 / Fs = -1.2576 - 1.9761 × ln(Qt)
kp = 221.419 - 1.401.7 × Qt + 2283.34 × Qt^2
1 / Qa = 0.4437 + 10.2652 × Qt^2 - 29.982 × Qt^3
Fb / Fs = 3.252 - 13.448 × Qt + 20.0398 × Qt^2
Fa / Fs = 4.4786 - 15.94 × Qt + 15.7596 × Qt^2
Class II Alignments
1/Qa has a correlation coefficient of 0.871
Vas / Vb = 16.883 - 69.941 × Qt + 75.2755 × Qt^2
F3 / Fs = 5.6721 - 15.168 × Qt + 10.6884 × Qt^2
kp = 9357.22 × e^(-15.987 × Qt)
1 / Qa = 1.3873 + 7.3126 × Qt^2 - 15.584 × Qt^3
Fb / Fs = 4.7413 - 12.556 × Qt + 9.4877 × Qt^2
Fa/Fs = -1.173 - 2.694 × ln(Qt)
[1] H.F. Olsen "Analysis of the effects of non linear elements upon the performance of back enclosed direct radiator loudspeaker mechanisms" AES journal, Vol 10, pp.156-162, (Apr 1962) [2] M.R. Gander "Moving coil loudspeaker topology as an indicator of linear excursion capability" AES journal, Vol 29, No ½, (Jan./Feb 1981). [3] R.H. Small "Vented box loudspeaker systems, Part II: Large signal analysis" AES journal, Vol 21, No 6 (Jul/Aug 1973). [4] J.J.M. Kreutz & J. Panzer "Derivation of the quasi Butterworth 5 alignments" AES journal, Vol. 42, No 5 (May 1994)
 Main Index
Main Index
 Articles Index
Articles Index