

|
| Elliott Sound Products | Project 64 |
This equaliser is designed as a preamp suitable for musical instruments - guitar, bass and keyboard in particular. Unlike most conventional graphic equalisers, each slider ranges from fully off to fully on, and not the more conventional +/-12dB or so that is normally available.
As a result, there is no flat setting (other than all off!). This graphic is designed to be used to create a sound, and is not suitable for hi-fi. It may be used as an add-on unit to existing instrument amp preamps, tone controls, etc. The flexibility is extraordinary, allowing a hollow 'single frequency' type sound, right through to almost any tonal variant imaginable.
This is the first of several projects based on the multiple-feedback bandpass filter described in Project 63, it can be made with as many (or as few) filter sections as you want.
Because of the repetitive nature of the filter units, I will be designing a PCB for them at some time in the future (depending on demand). One board will carry two or 4 filters, and the boards will be quite small so they can be packed into a case easily. The remainder of the circuitry can easily be constructed on Veroboard or similar.
The input circuit is completely conventional, and uses 1/2 of a dual opamp as the initial gain stage. This is followed by the volume control, second gain stage and buffer. The output of the buffer is fed to the inputs of the filter stages, each of which has a slider for its specific frequency. The outputs of the sliders are summed using another opamp, and a distortion effect is included in the final output stage. This can be left out altogether if distortion is not desired.
If used for guitar, the frequencies needed only have to range from 80Hz to about 7kHz, but to make the unit more versatile I suggest that the lowest frequency should be 31Hz, and the highest around 12kHz. This can be extended if you want.
Decisions!
Now you have to decide on the frequency resolution. 1/3 octave would be really nice, but the number of sliders can be a nightmare. At the very least, you will need octave band, and the suggested frequencies are ...
31 63 125 250 500 1k0 2k0 4k0 8k0 16k
Should you decide on 1/2 octave band frequencies, 20 sliders will cover the range suggested (plus a bit) - these might be ...
31 44 63 87 125 175 250 350 500 700 1k0 1k4 2k0 2k8 4k0 5k6 8k0 11k 16k 20k
The 20kHz filter can be (should be?) left off for instrument use, so that means only 19 slide pots will be needed. Lastly, 1/3 octave band needs 30 sliders to cover the full frequency range, but the 25Hz and 20kHz bands will not be needed. This still requires 28 slide pots, but the flexibility is greater than you will ever get with conventional tone controls ...
31 40 50 63 80 100 125 160 200 250 315 400 500 630 800 1k0 1k2 1k6 2k0 2k5 3k2 4k0 5k0 6k3 8k0 10k 12k 16k
There is no reason at all that the unit has to be 1/2 octave or 1/3 octave all the way. The midrange can be 1/3 octave for finest control, but go to 1/2 octave at the extremes. Especially for guitar and bass, I would prefer 1/3 octave up to 1kHz, then 1/2 octave from 1kHz to 8kHz. The final slider would be a 1 octave band filter at 16kHz. The sequence now looks like this ...
31 40 50 63 80 100 125 160 200 250 315 400 500 630 800 1k0 1k4 2k0 2k8 4k0 5k6 8k0 16k
This gives 23 filters and slide pots, a reasonable compromise that should give excellent results. To ensure reasonable continuity, the filters at 1kHz and 8kHz will need to be a compromise. 1/3 octave filters need a Q of 4, and 1/2 octave filters use a Q of 3, so the 1kHz filter will actually have a Q of 3, and the 8kHz filter will be best with a Q of 2. This might look daunting, but the MFB Filter design program will make short work of determining the component values. Unfortunately, this is only available for users of Microsoft Windows. Note that you will also need the Visual Basic 4 (VB4) runtime library, which can be obtained from the Microsoft support Website.
If you want to use the frequencies shown above, the table at the end of this page shows the values for each filter.
The Circuit
Figure 1 shows the schematic of the input section, and is virtually identical to the guitar preamp presented in Project 27. The two input jacks allow rudimentary mixing of two sources, but are mainly designed to provide a high gain and a low gain input to help prevent input stage overload. The 'Hi' input connects the signal directly to the opamp input, and the 'Lo' introduces a 6dB loss to allow for high output pickups. The buffer stage has an effective load of about 810 ohms - a difficult load for an opamp to drive. I suggest that an NE5532 opamp is used for U1, as it is one of the few that can drive such a load without difficulty. Although a TL072 can be used, this should be for testing or as a last resort. Pinouts are the same for both types, but the NE5532 is more critical of supply bypassing, and the addition of 100nF ceramic caps from each supply to ground is strongly recommended (as shown). These should be as close to the IC package as possible.

Figure 1 - Instrument Equaliser Input Stage & Buffer
The filters and slider pots (with their mixing resistors) are shown in Figure 2. To see the actual filter circuit, refer to Project 63, it is far too cumbersome to draw each of these in full! Even so, only six of the 23 filters are shown. There is one filter module and one slider for each frequency. For guitar especially, you might want to provide more gain for the higher frequencies (typically from about 2kHz to 8kHz). No problem. Since the mixing resistors are nominally 100k, starting from the 1k4 slider, drop the value to 82k, then use 47k resistors for the remaining bands. This gives a 6dB increase in top-end boost which should be sufficient (you can have more, but this will increase the noise level).
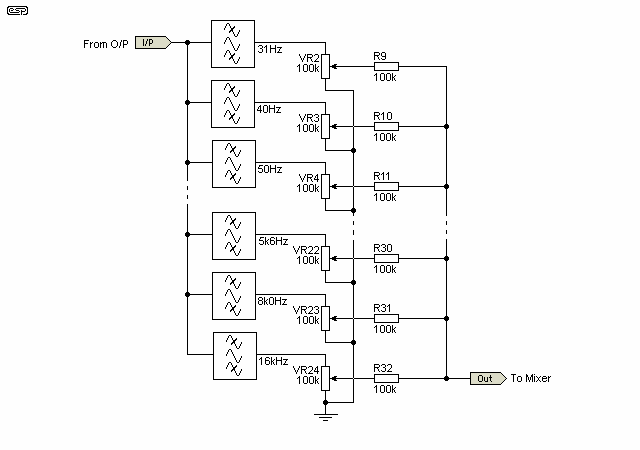
Figure 2 - Filter Bank (Part), Slide Pots and Mixing Resistors
The filters do not need really quiet opamps, and considering the number this would be prohibitively expensive. The opamps do need to be at least to the standard of the TL072 or filter performance will suffer. The suggested frequency ranges will give good performance at all frequencies, since the Q (and hence the demands on the opamps) is reduced as the frequency increases.
Finally, the mixer and output stage are shown in Figure 3. The mixer is a conventional 'virtual earth' type, and minimises interaction between the slide pots. The distortion stage uses the diodes (all 1N4148 types) as a clipping circuit, and in conjunction with VR24 (Master Volume) allows the amount of distortion to be adjusted from zero to 'heavy metal' (aka 'grunge'). It may be necessary to use more diodes than the 4 shown. An additional 4 diodes will raise the maximum output level to about 1,5V RMS before clipping starts. The final opamp is a buffer, and contributes no gain.
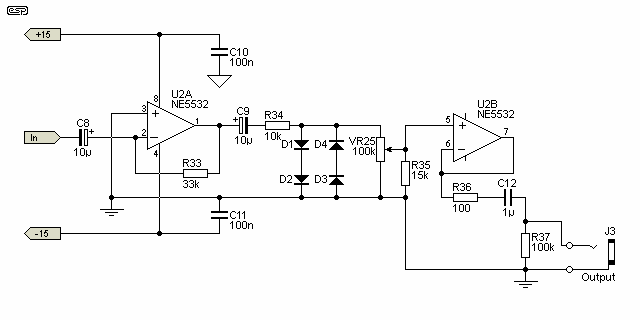
Figure 3 - Mixer and Distortion Circuits
A word of warning. Don't expect this preamp to be especially quiet, because it won't be. Use of a low noise opamp for the mixer helps, but as with all guitar amps, some noise is inevitable. This is made worse by all the filter circuits, but each only adds noise in its own band, so the cumulative noise is not as great as it might be. Using the distortion control will increase noise, and this can be dramatic at full distortion. In reality, this is not much different from a conventional guitar preamp that is turned up LOUD to get the same distortion. The more gain you have, the greater the noise (ye cannae change the laws of physics!).
Using the equaliser is simplicity itself. Just slide sliders up and down to get the sound you want. There is no 'correct' way to use this unit - it is designed to enable you to get sounds. As described above, you can get more of any given frequency by reducing the value of the mixing resistor, but there is a limit to how much noise is tolerable.
The total gain of the unit (with all sliders at maximum) is about 15 times for the input stage, and a further 7.6 for the mixer (using all 100k resistors). This gives a total gain of 113 (or 41dB). Actual gain will be different, depending on the slider setting, and can be increased (or reduced) by changing the value of R33 (lower the value for less gain and vice versa) or R7 (lower value gives more gain). If you change the gain structure, be careful that the input gain is not made too high, or you will get distortion with high output pickups.
To power the circuit, any power supply capable of +/-15V (+/-12V at a pinch) will do, provided that it is capable of 100mA or so.
The table shows the values I calculated for each filter. Component references are based on the diagram in Project 63, which is reproduced here for convenience (pin connections are not shown). For this application, omit C3, R4 and short the non-inverting opamp input to ground.
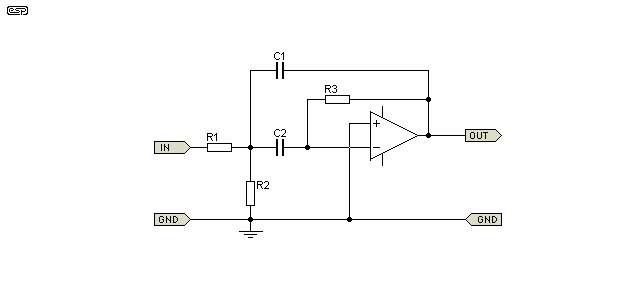
Figure 4 - Multiple Feedback Bandpass Filter
| Freq | R1 | R2 | R3 | C1, C2 | Freq | R1 | R2 | R3 | C1, C2 |
| 31 | 82k | 2k7 | 160k | 220nF | 500 | 27k | 820 | 56k | 47nF |
| 40 | 82k | 2k7 | 160k | 180nF | 630 | 27k | 820 | 56k | 39nF |
| 50 | 82k | 2k7 | 160k | 150nF | 800 | 27k | 820 | 56k | 27nF+2n7 |
| 63 | 82k | 2k7 | 160k | 120nF | 1k0 | 8k2 | 510 | 18k | 47nF+4n7 |
| 80 | 82k | 2k7 | 160k | 100nF | 1k4 | 8k2 | 510 | 18k | 39nF |
| 100 | 82k | 2k7 | 160k | 82nF | 2k0 | 8k2 | 510 | 18k | 27nF |
| 125 | 82k | 2k7 | 160k | 56nF+5n6 | 2k8 | 8k2 | 510 | 18k | 18nF+1n5 |
| 160 | 82k | 2k7 | 160k | 47nF | 4k0 | 8k2 | 510 | 18k | 12nF+1n8 |
| 200 | 82k | 2k7 | 160k | 39nF | 5k6 | 8k2 | 750 | 18k | 8n2 |
| 250 | 82k | 2k7 | 160k | 27nF+4n7 | 8k0 | 8k2 | 1k2 | 18k | 4n7 |
| 315 | 82k | 2k7 | 160k | 22nF+2n7 | 16k | 8k2 | 1k2 | 18k | 2n2 |
| 400 | 82k | 2k7 | 160k | 18nF+1n5 |
I have tried to keep the values reasonably sensible. This is not easy with 1/3 octave band equalisers, but all in all the results are quite acceptable, with not too many different values. It will be apparent that some capacitor values can't be obtained from a single cap, so two are used in parallel (e.g. 56nF+5.6nF = 61.6nF). Note that the Q of the filters is changed as the frequency increases - feel free to use the calculator to reverse calculate the values to see the actual gain, Q and frequency error. None of these will be significant in use.
The frequencies in bold are likely to be good candidates for guitar and bass, where a 1/3 Octave equaliser isn't warranted. Naturally, you may change these around to suit yourself, and remember that the component values will need to be changed to reduce the filter Q (they are too sharp for octave band EQ).
 Main Index
Main Index
 Projects Index
Projects Index