

|
| Elliott Sound Products | Project 179 |
 )
)Some years ago, too many to contemplate, I built an oscillator with low distortion with the aim of using it to test various amplifiers. It was based on a Wien bridge for simplicity, which is shown in outline in Figure 2, and used the R53 thermistor which was designed for amplitude stabilisation in such oscillators. It worked pretty well for a decade or so, and I designed a second unit with extended capabilities, namely 1Hz- 1MHz range. For this I purchased an RA53, which was basically the R53 in a smaller envelope (Figure 1).

Figure 1 - R53 Thermistor (Top), RA53 Thermistor (Bottom)
Those of you familiar with the Wien bridge will know that the operating frequency is given by, for equal resistors and capacitors in the phase lead and lag arms (R1=R2=R and C1=C2=C in Figure 2). That boils down to requiring a time constant (R × C) of 15.9ms for a frequency of 10Hz. Frequency is determined by ...
f = 1 / ( 2π × R × C )
As a result, my original design used a widely available 10k dual-gang pot, and capacitors of 1.5µF and lower decade values, with a limiting 1k resistor so that the nominal lowest frequency is set by 11k and 1.5µF to just under 10Hz. The original circuit was incapable of running at higher frequencies than about 100kHz, so that is where it stopped.
Many contemporary commercial oscillators of similar concept used odd values of potentiometer such as 15k, which are almost impossible to source. To extend the range to 1Hz but keeping capacitor values to a maximum reasonable size of 10µF required 15.9k which I decided to construct using a series 1.5k limiting resistor, then three dual gang pots of 2.2k, 4.7k and 10k giving fine control of the upper frequency ranges. The first thermistor to die was the one in this oscillator, the RA53. By this time, the R53 was extinct and the RA53 hard to find. There were occasional sightings of these animals at a cost of £11 which in today's money would be about £30 (roughly AU$54 at the time of writing).
For expediency, I raided the R53 from the first design to keep the second alive. But after another few years, the amplitude became unsteady. I traced the prime cause at the time to noisy pots, a very common issue with pots over about 10 years old (or earlier with lower quality units). Now, the 2.2k dual pot had vanished, so I replaced that with a 1k dual pot, and recalibrated the front panel scales. (For calibrated frequencies, the pots had to be turned fully clockwise in sequence before changing the next on the right, going up, and conversely fully anti-clockwise before turning the next on to the left when going down). The repair was however short lived as the thermistor then died. In hindsight some of the poor amplitude control may have been due to the thermistor aging.

Figure 2 - General Form Of Wien Bridge Oscillator
I was now faced with no test oscillators, even simple ones, for quick checking. That is when I 'bit the bullet' and went for a low distortion, low bounce oscillator based on IC op-amps with three phases, a six-phase rectifier and LED/LDR control loop. However, that has a frequency range of only 1Hz-30kHz and at 30kHz even the op-amp distortion is not so low. However, that is another story.
To test the bandwidth of amplifiers I really needed the 1MHz response of my 'old faithful' (until it wasn't) Wien bridge. The only practical solution to restoring this was to use a filament lamp. I measured the resistance against current for a number of filament lamps between 6V and 24V. For the higher voltage lamps, not much change in resistance is apparent until at least 1V is reached. Perhaps that is not surprising, since power dissipation in a resistor is proportional to the volts squared (P = V2 / R) and below 1V the V2 term gets smaller quite quickly.
If 1V is required, that implies a peak of 1.414V, and in a Wien bridge a gain of 3 is needed, so that makes the output voltage 4.24V (peak) which would be more than the circuit, which operated from two 6V batteries, could manage without distorting, or in this case, specifically clipping. Of course, starting from a clean sheet it may be preferable to use a higher supply voltage as the current drawn by a 24V lamp is low.
Of the 6V lamps I had, the 40mA unit was a good choice, as it has a high resistance and as a result a reasonably high working resistance but I found that the lowest commercially available lamp is now 60mA. So yet another component has obsoleted itself without my permission! The measured IV curve, with its measurement random kinks, for the 60mA (360mW) lamp is shown in Figure 3.

Figure 3 - Lamp Resistance Vs. Current
At 60mA and 6V the working resistance is normally 100 ohms. But at low voltages where there is no heating, it is about 10 ohms or one tenth of the hot value. This is quite typical of all tungsten lamps. From this characterisation, this lamp shows a significant change of resistance at around 300mV, corresponding to about 15mA current and a resistance of 25 ohms. This is the onset of substantial self-heating. Now, filament lamps of the MES type have a limited life, typically only 100 hours at its rated power. But when run at very low voltages, the filament reaches only a few hundred degrees C and will last much longer. It is desirable to run the filament at a temperature well above ambient so that changes in ambient have little effect on the output voltage, and a few hundred degrees is not a problem.
One of the ever-present issues with filament lamp, or thermistor stabilised oscillators for that matter, is of amplitude bounce. This is where the output voltage is initially low, so the feedback mechanism is designed to give a high gain, or at least something sufficiently higher than the required 3x in order to start the oscillations reliably. But the thermistor or lamp takes a few (to tens of) milliseconds to respond, and if the amplitude in this time has reached a high value the controlling element over-reacts, and shuts the oscillations down because the gain then falls below 3. The oscillator cannot then oscillate until the control element's resistance has allowed the gain to become over 3 again. Instead of a nice steady signal we get an amplitude modulation between zero and clipping, in the worst case.
At low frequencies, there is an additional problem in that the control element can respond within the period of the oscillation. For, say, 1 Hz, this means that during the peak of the signal, the resistance can actually change and limit the gain. Since this will be at the highest voltage, in effect the peaks will be clipped. If not clipped, then at least partly flattened, which corresponds to 3rd harmonic distortion. What is desired is that the control path operates on the average signal, but not within the time period. This conflict of interest cannot be solved using a single controller, which is why multi-phase systems, or sample-and-hold control loops are needed for low distortion, especially at low frequencies.
However, the worst effects of amplitude bounce and distortion can be ameliorated using a simple trick of diluting the feedback so that the thermistor, or lamp, provides a minor, or trimming, effect on the overall feedback. The scheme is illustrated in Figure 4. A feedback network consists of R1 and R2 which set the gain to just over 3 to ensure reliable start-up of the oscillation. Additional feedback is provided through a voltage divider, consisting of R3 and the filament lamp Lp1, which couples into the feedback point through resistor R4. In this way, if R4 is larger than R2, the feedback from the lamp is a smaller fraction than it would be were the whole output voltage used to feedback the amplitude. There is however a secondary consideration to this. That is, the lamp voltage is run at a higher proportion of the output voltage than it would be normally.

Figure 4 - Lamp Resistor Network
Refer to Figure 2, when a thermistor (Th1) is used as the negative feedback amplitude controller. It operates in conjunction with the 'grounding' resistor Rg. In this case, if the output voltage increases, the voltage across the thermistor increases and raises the power in the device. Having a negative temperature coefficient of resistance (TCR) its resistance reduces, increasing the feedback, and (in principle) stabilising the output. In the case of the filament lamp, it has a positive TCR so this has to be used in place of Rg and a fixed resistor in place of the thermistor: they swap places in other words. For a gain of 3x, the lamp would therefore run normally at one-third of the output voltage. In the case where the feedback from the lamp is 'diluted', the lamp voltage runs at a higher fraction of the output. If we choose 1V as the target output voltage, the lamp could run at 0.5V which corresponds to 30 ohms and 17mA from the results in Figure 4. This would actually increase the third harmonic distortion but the dilution effect means that the lamp voltage is attenuated by a factor of about 5, and the overall distortion is still lower than it would have been.
And now the downsides. One of the attractions of the thermistor was that it was a very low power device. You can just make out the tiny beads that were the actual thermistors in the glass bulbs in Figure 2. It only needed a current of a few mA to heat up, as a result. Using a filament lamp of only 6V requires significantly more current – 17mA (RMS, too) – as previously determined. As a result I had to change pretty much every component in the circuit, though the basic circuit architecture was retained. I took the opportunity to add a current mirror to the input stage to improve the open loop gain and reduce distortion, and used a simple Miller capacitor to stabilise the high frequency performance, without which there is a 15MHz-ish peak which could give rise to undesired oscillation.
The basic architecture of the amplifier is a differential input stage, current mirror, single-ended driver and complementary output transistors operating in Class A for low distortion. I had tried using FETs in the front end but second harmonic distortion remained excessive, even after the compensation afforded by the differential stage. The problem was traced as far as exploring a single FET distortion characteristics, then a differential, and I found that unlike the simulations, the differential circuit only partially reduced the second harmonic, which was approximately ten times that expected from simulation, which as first order theory would suggest, should have all but been eliminated. Therefore, I chose to stay with bipolars. In order to obtain a good performance at low frequencies, a base bias current needed to be provided so that no electrolytic capacitors were required (other than a couple of power supply decoupling caps). The original capacitors were now over 20 years old, and showing signs of aging (domed end cap in one case), so were retired. The base bias current is provided by an adjustable current source provided by an additional transistor. The complete circuit, apart from the timing components and output control, is shown in Figure 5.
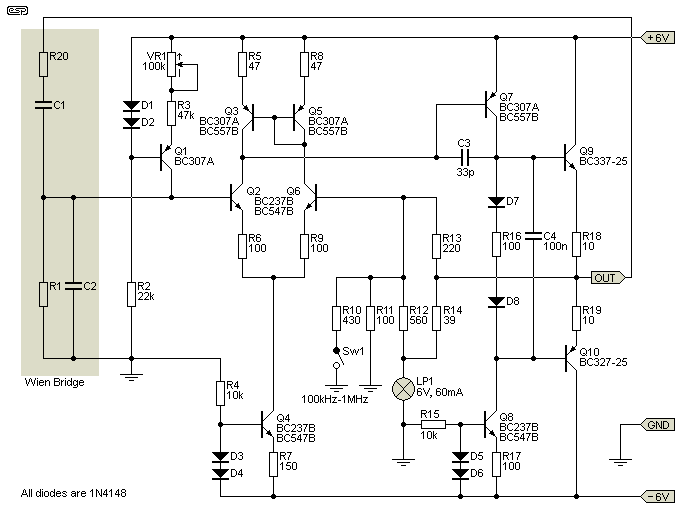
Figure 5 - Complete Circuit Of Oscillator Amplifier
The basic architecture of the amplifier is a differential input stage, current mirror, single-ended driver and complementary output transistors operating in Class A for low distortion. I had tried using FETs in the front end but second harmonic distortion remained excessive, even after the compensation afforded by the differential stage. The problem was traced as far as exploring a single FET distortion characteristics, then a differential, and I found that unlike the simulations, the differential circuit only partially reduced the second harmonic, which was approximately ten times that expected from simulation, which as first order theory would suggest, should have all but been eliminated. Therefore, I chose to stay with bipolars.
In order to obtain a good performance at low frequencies, a base bias current needed to be provided so that no electrolytic capacitors were required (other than a couple of power supply decoupling caps). The original capacitors were now over 20 years old, and showing signs of aging (domed end cap in one case), so were retired. The base bias current is provided by an adjustable current source provided by an additional transistor. The complete circuit, apart from the timing components and output control, is shown in Figure 5.
Transistors Q2 and Q6 form a differential pair with 100 ohm emitter degeneration resistors. These are fed from a simple constant current source formed from Q4, resistor R4 and diodes D3 and D4. A bias current for Q2 is provided by Q1 which is also a current source, but PNP and fed from the positive rail. This operates at a few microamps but is adjustable to suit various transistors. The differential pair operate into a current mirror consisting of Q3 and Q5. These feed a driver transistor Q7 which is a PNP operating in common emitter. It too is fed from a third constant current source, Q8, set to a current of 6mA.
A bias network consisting of diodes D7, D8 and R18 provide approximately 600mV of additional bias to the complementary output pair which have 10 ohm emitter resistors, and this sets the current in the output stage to 30mA. This is sufficient to provide 24mA peak output into the feedback network, noting that each transistor only has to swing by half this and that keeps the distortion manageable. In fact the feedback network is the greatest load as the output is taken to a potentiometer ('volume control') a single gang, 1k pot, which is not shown, but very useful for controlling the output signal.
The choice of transistors is not particularly critical. The current mirror and base bias PNP transistors can be BC307s, as in the original, or, as these are now obsolete, the alternative BC557 of any gain variety but the mirror pair should be matched. The input pair should be BC547Bs and the PNP driver transistor should also be the 'B' grade gain for low distortion. I tend to buy grade B types and use these for all small signal circuits. The output pair should be the higher power BC337 and BC327 devices as they have better current handling capability than the BC547/557 devices. If possible use the higher grade gain groups -25 or -40 for lower distortion.
Stabilisation is provided by a 33pF Miller capacitor to cut the gain beyond a few MHz. Some readers may know that Miller stabilisation is not my (i.e. John's) preferred choice for an audio amplifier but in an oscillator, sinewaves are well behaved and as single frequencies are needed the behaviour is predictable. In this instance, the 33pF only burdens the driver by about 0.6mA at 1MHz and therefore does not cause slew rate distortion, though it does reduce the open loop gain (see later).
The feedback network was optimised for 1V RMS output, in accordance with the original design. The lamp runs at just below 0.5V, and the combination of 39 ohms limiting the signal and a 560 ohm feedback resistor was sufficient to maintain oscillations with minimal bounce. That is not to say that bounce has been eliminated, but it is well controlled and does not take more than a few cycles. At low frequencies, as discussed, the lamp follows the signal and provides real-time control. As a result, there is almost no bounce, unlike the original thermistor design which bounced for longer at low frequencies. The consequence is however higher distortion. It should be noted that the main feedback resistors, R11 and R13, should be 1% tolerance or there could be insufficient gain to start oscillations.
The frequency control components are represented by R1, R20, C1 and C2. In practice the resistors are a 1.5k fixed resistor, in series with a 4.7k and 10k dual-gang potentiometers to generate up to 16k in principle. While ordinary 10% or 20% components can be used, there is a possibility that the lowest frequencies might not be achieved if the resistances are lower than advertised. For best results, tight tolerance components are preferred, and a third potentiometer, 1k, can be used to offset the low end tolerance range, as now used in my modified oscillator. These give a 10:1 working range.
The capacitors required for the various frequency ranges are connected using a two-pole, 6-way switch but there is a caveat. The capacitors used originally, and still used, are 10µF, 1µF, 100nF, 10nF, 1nF. Although 100pF would seem optimum for the top range, it required 68pF to ensure the frequencies were achieved. These cover the ranges as follows:
| Range | Capacitors C1 and C2 | Frequency |
| 1 | 10µF | 1.0-10 Hz |
| 2 | 1µF | 10-100Hz |
| 3 | 100nF | 100Hz-1kHz |
| 4 | 10nF | 1kHz-10kHz |
| 5 | 1nF | 10kHz-100kHz |
| 6 | 68pF | 100kHz-1MHz |
Now the caveats. Due to the Miller compensation, the open loop gain falls to lower values at higher frequencies. The critical split-feedback network relies on a high open loop gain to start oscillations, and in the top decade, is too low as it stands. This is corrected using a supplementary switch (Sw1) which boosts the gain sufficiently by connecting a 430 ohm resistor in parallel with R11. Because the capacitor switch I had already wired up with the two-pole 6 position was difficult to change (no room for an alternative) a separate switch was added. Starting from a blank sheet, a multi-wafer switch should be used, so that an additional switch bank can be added that would switch this resistor in at the top end, and leave open circuit for the other positions.
An additional switch bank would also be extremely useful to adjust the output level in the lowest frequency range. Because the lamp corrects the amplitude in real time, the peak output reaches a higher voltage than the levels of the other ranges, and on my circuit provided 1.4V RMS at 1Hz. Therefore, for this range (1-10Hz) it would be useful to switch in an additional resistor in series with R11 to reduce the amplitude a little.
Setting up is quite straightforward. The control potentiometers are set to minimum resistance (highest frequency) on one of the lower ranges, and the DC output voltage measured. To avoid large AC signals entering your meter, these can be filtered with a 1k and 100uF reversible electrolytic. The pots are then turned to maximum resistance (lowest frequency) and the bias current adjusted to bring the DC offset back to the starting value. If it is necessary to reduce the offset further (typically this is only a few mV) then the emitter degeneration resistors of 100 ohms can be changed to 91 ohms and a 10 or 22 ohm potentiometer added with the wiper taken to the current source. (See Editor's Comments for more info on setting the bias current.)
The measured performance is now at least as good or rather better than the original. At 1Hz the THD was 1% and largely third harmonic, which reduced significantly in the 10-100Hz range. Here is a table of results:
| Range | Frequency | Output | 2nd | 3rd | 4th | 5th |
| 1 | 0.84Hz | 1.4 | 1mV | 15mV | 140µV | 1mV |
| 2 | 8.5Hz | 1.2 | 144µV | 1.0mV | < noise | < noise |
| 3 | 84Hz | 1.14V | < noise | 110µV | < noise | < noise |
| 4 | 863Hz | 1.1V | < noise | < noise | < noise | < noise |
| 5 | 8.25kHz | 1.07 | 77µV | < noise | < noise | < noise |
| 5 | 19.75kHz | 1.2 | 92µV | < noise | < noise | < noise |
Table 2 shows an analysis of distortion components for the lowest frequencies on each range, except for range 5 where two frequencies are given, but no distortion components were able to be measured on range 6, which is likely to increase again. The output voltage variation is largely due to tolerances in component values, but in all cases the output voltage was at least 1V.
The measurement system noise floor is rather limited by today's standards, at around 40µV, or 0.004%. But for a relatively simple test oscillator to provide basic signals, this is actually a good result.
The final comment here is that the compromise over the original circuit is that the battery current drain is now higher, approaching about 40mA. Despite this, it is still recommended to operate the oscillator on batteries as this saves all sorts of earth loop issues when testing amplifiers. A couple of 4-cell battery holders for AA alkaline cells is capable of operating the oscillator for at least a day (the cut-off point is shorter than the published cell data which quotes the capacity to 0.8V). It could be worth considering using C or D cells if starting from a blank sheet. The best policy is to remember to switch off immediately after use.
The text in this article is almost identical to the original, but I changed the transistor designations in both the text and drawings to align with common practice on the ESP website. A small number of other changes were made, mainly in formatting and the order of some of the text and drawings. All drawings have been re-done to 'normal' ESP style, and the photo (Figure 1) is 'as supplied', but resized slightly. It's also worth pointing out (as I did in the Sinewave Generators article), that generating a high quality (low distortion) sinewave is not a simple task!
One thing that needs to be highlighted is that the resistor network (R12, R13 and R14) may need to be adjusted to suit the lamp being used. Small filament lamps are not precision components, and show some variation even within the same batch. If you use something different (as is likely), then you will need to experiment a little to ensure reliable oscillation and minimum distortion. One of the things that affects the gain requirement is the tolerance of the tuning caps and pots - the requirement for a gain of 3 only applies when the resistance and capacitance are well matched. Even relatively small variations (ca. 1%) mean that the gain must be changed slightly to ensure oscillation and/or minimum distortion. Amplitude bounce after changing the frequency is a direct result of imperfect tracking of the tuning potentiometer gangs.
It's mentioned in the text, but you may miss the fact that the dual-gang tuning potentiometer (including series resistors) requires a total resistance of 15.9k (~16k in total). John achieved this with series pots (originally 2.2k, 4.7k and 10k, but then changed to 1.5k fixed, in series with 4.7k and 10k dual-gang pots). 4.7k pots are now (generally) 5k, and even they may be hard to find now. This arrangement allows coarse, fine and very fine tuning using three pots. With two pots, you get coarse and fine adjustment.
You may need to re-calculate the capacitances used to allow the use of a single dual-gang pot (with series resistance). For example, a 10k pot with 1k series resistance gives a low frequency range of 1.44Hz to 15.9Hz using 10µF, caps, with higher ranges in multiples of ten. The highest frequency available is (nominally) 1.59MHz. You might decide to use caps of 15µF, 1.5µF, 150nF, 15nF, 1.5nF and 150pF to achieve the ranges described. Note that the 150pF caps may need to be reduced to account for stray capacitance. Do not use bipolar electrolytic caps for tuning the low frequency ranges, as they are not stable enough and will almost certainly increase distortion to unacceptable levels. Polyester caps are the minimum requirement, but in this role I recommend polypropylene. Test equipment requires performance levels that are better than the equipment being tested.
Note that despite the current source based on Q1, the offset can never be cancelled completely. This is because the resistance from the base of Q2 varies as the frequency is changed. However, if VR1 is adjusted carefully (with the Wien bridge feedback resistor R20 disconnected), DC offset should be able to be trimmed to give less than 1mV DC at any frequency pot setting. This adjustment needs to be done without oscillation because it's very difficult to set properly in the presence of the sinewave output. VR1 must be a multiturn trimpot, because the setting is quite critical. Adjustment is a reiterative process, requiring small changes as the frequency pot(s) are varied from maximum to minimum and vice versa. In practice, the Q1 current needed will be around 7µA.
A further comment concerns the battery arrangement. Constructors may wish to contemplate Li-Ion batteries. The disadvantage is that the charging regime is more complex, because a balance charger is absolutely essential for a series battery pack. The alternative is to use 4 × 18650 cells (18mm diameter × 65mm long), which can be removed and charged in parallel. Chargers and 4-cell holders for these are readily available, and this eliminates the complexities encountered with series charging. With a typical capacity of around 3,500mA/H and with a 40mA current drain, you should get close to 90 hours of continuous use before re-charging is necessary. If 'protected' calls are used, there is no need to add a voltage cutout, as the cells have this built-in. However, despite the same size nomenclature (18650), protected cells are usually closer to 70mm long, so the cell holder must be able to accommodate the extra length.
I make this suggestion having recently tested my 'stash' of Ni-MH cells, and found that most had to be sent off to the local recycling depot. I also have a small stash of AA and 18650 sized Li-Ion cells, and every one of them is in perfect order. My 'everyday' digital camera uses two AA size Li-Ion cells (plus two 'dummy' cells), and it runs for several weeks to a couple of months at a time before a re-charge is needed. Ni-MH don't last anywhere near as long because of the very point that John made - the cutout voltage is only 0.8V/ cell, and the nominal operating voltage is only ±4.8V for eight cells, making them unusable. Alkaline cells are better, but naturally have to be tossed (or preferably recycled) at depressingly regular intervals. Also, woe-betide you should the battery be left in place after discharge, as the internal fluids can make a right-royal mess of your pride and joy when (not 'if' !) the cells decide to leak. While 18650 cells are not inexpensive, if charged properly they will last a long time without problems.
 Main Index
Main Index
 Projects Index
Projects Index