

|
| Elliott Sound Products | Speaker Current Drive |
 Main Index
Main Index
 Articles Index
Articles Index
This topic has been looked at in a couple of articles/ projects, but it's something that creates problems for people, as it always seems to sound 'better' when applied to any given loudspeaker driver or system. In the article/ project Variable Amplifier Impedance (aka Project 56) the basics of both positive and negative impedance are covered, but here we will only look at positive impedance because negative impedance has too many ... negatives  . As discussed in the article, negative impedance is inherently unstable, and that's not something you want when driving a loudspeaker.
. As discussed in the article, negative impedance is inherently unstable, and that's not something you want when driving a loudspeaker.
This is for the experimenter, and the results can be worthwhile if it's done properly. For example, for any number of reasons, it may be advantageous to build a speaker box that's a little too big for the driver (as determined by the Thiele/ Small parameters, and modelled in WinISD or similar). If the driver's Qts is increased by driving it with a higher than normal (i.e. greater than zero ohms) impedance, everything falls back into place, and a useful extension to the low frequency -3dB point can be achieved. Surprisingly, this can work with vented (ported) enclosures as well, but the results are less predictable. Damping is especially troublesome with a vented box.
The idea of being able to vary the output impedance of a power amplifier has been around for a long time. I have used these techniques since the early 1970s in various designs, and much as I would like to be able to claim otherwise, I was by no means the first. In some cases (especially in the early years), it's likely that the high output impedance was 'accidental', in that the makers of some of the equipment weren't at the highest skill levels, and just copied what someone else had done before them. The end result worked, so it wasn't given another thought.
Current drive (or at least a modified form thereof) is used to drive spring reverb units, and various other transducers where a constant current is either preferable or essential, and where voltage drive is inappropriate. For many years (even before transistor amps), voltage drive has been what we all strive for with power amplifiers - a perfect (ideal) voltage amplifier has zero ohms output impedance, and the amplitude does not change as the load varies. Loudspeakers are very non-linear loads, and the impedance will change at different frequencies for all sorts of reasons. Voltage drive has an advantage, because it is easy to achieve (down to well below 0.2Ω) and, most importantly, it is easy to achieve consistent results.
'True' current drive has a high impedance, which may be several thousand ohms or more. Despite simplistic circuits you might come across, it can be difficult to achieve, and amplifiers designed for such high impedances should ideally be installed in (or on) the loudspeaker cabinet. Disconnection of the speaker can result in the amplifier's output voltage swinging to one or the other rail voltage, because there is no feedback. Extreme care is needed to ensure that the amplifier's gain is properly matched to the speaker driver, because the two are inextricably linked. Even a small change of speaker characteristics can cause a fairly substantial level change, at one or more frequencies.
This article mainly covers 'mixed mode' feedback, which provides a defined source impedance to the drivers. This is not current drive, and isn't intended to be. There are some 'interesting' challenges to building an amplifier that has a particularly high output impedance, not the least of which is the likelihood of DC offset which ideally should be maintained at less than 50mV (or less than 10mA) into a nominal 8Ω load.
Based on available literature, the use of current drive (very high amplifier impedance) does appear to improve some aspects of loudspeakers. However, it's entirely up to readers to look through the references and make a decision for themselves. I make no firm claims one way or the other, but merely look at the current 'state of the art', and examine ways to achieve a desired output impedance. To some extent, there seems little doubt that current drive does improve performance, but what matters is whether it can be made to work in a real loudspeaker system. Of course, it also depends on whether the 'improvements' are audible, assuming that identical frequency response can be achieved with both voltage and current drive. This is difficult because so many aspects of the driver(s) change dramatically depending on the source impedance.
A loudspeaker responds to current, not voltage. When a voltage is impressed across the voicecoil, a current flows that is directly related to the impedance at that frequency, and it is the current flow that creates the voicecoil movement. A moving coil loudspeaker will generate a back-EMF whenever the impedance is inductive, seen as impedance rising with increasing frequency. The back-EMF opposes the applied current. Above resonance (impedance falling with increasing frequency), the speaker appears as a capacitive load. These complex interactions are responsible for the impedance curve seen for any loudspeaker. Adding a vent to the enclosure adds to the complexity by including another resonance, this time due to the enclosure tuning and dictated by the air mass within the enclosure and vent.
A typical driver is resistive at two frequencies only. At the resonant peak the impedance is purely resistive, and the same is true at a frequency between resonance and where the impedance starts to rise due to the voicecoil's semi-inductance. The voicecoil is not a 'true' inductance because it's influenced by eddy currents in the steel pole pieces. This resistive frequency is the lowest impedance shown on the curve, and is usually between 200Hz and 400Hz. The voicecoil along with the attached cone and spider (etc.) form a mechanical resonance that is reflected back to the source. There are non-linearities in all the mechanical components, and further electrical non-linearities are caused by the magnetic structure.
The so-called 'damping factor' quoted by amplifier makers only has an effect at the speaker's resonance. This is the point where the impedance it its greatest, and by applying an effective short circuit (by the amplifier), the resonance is damped. However, the damping is limited by the voicecoil resistance, which is in series with the 'resonant circuit'. This resonant circuit is seen in Figure 1, with the components shown as Lp, Cp and Rp. Rp is a special case, and is basically the value of impedance at resonance (plus the voicecoil resistance (Rvc) to be exact). It's due to mechanical losses in the cone, surround and spider. The woofer shown in Figure 1 shows an impedance of 47Ω at resonance. Note that the rather low resonant frequency is simply due to the model used, and the actual frequency is of little consequence. The same effects are produced regardless.
Voltage drive (the most common by far) maintains a constant voltage across the load, regardless of impedance variations. Consider the simple loudspeaker system shown below. The woofer and tweeter use a simple passive series crossover network, consisting of L1 and C1. The equivalent circuits of the two drivers are included, and while these do not represent any particular drivers, they are reasonably close to 'typical' values that you might determine by analysis.
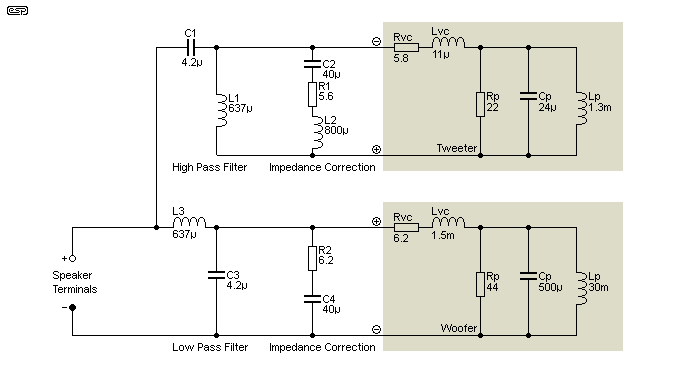
Figure 1 - Two Way Loudspeaker Schematic
The crossover is at 3.17kHz, and is a relatively conventional Linkwitz-Riley 12dB/ octave design. It includes compensation for the tweeter's resonance, as well as impedance compensation for the woofer. This ensure that the woofer's impedance remains flat across the crossover frequency to prevent response aberrations. The impedance compensation networks are indicated on the drawing. There are several articles on the ESP site that deal with crossover networks, and for this exercise we'll stay with this 12dB/ octave network. As always, one driver must be connected in reverse phase due to the phase behaviour of the crossover itself.
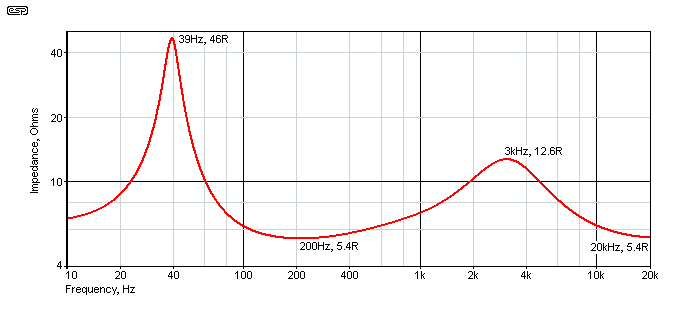
Figure 2 - Two Way Loudspeaker Impedance Curve
The impedance curve is much as one would expect, and when this speaker is driven from a voltage amp (low Z out) it will (or should) sound just the way you'd hope for. The two electrical signals (woofer + tweeter) sum flat when driven by a voltage amplifier. We need to examine the power delivered to the system, so first we'll look at using 'conventional' voltage drive.
If we assume a nominal power of 1W (2.83V RMS into 8Ω), the power at 200Hz is 1.44W because the impedance is less than 8Ω. At woofer resonance (39Hz), the impedance is 46Ω, so power is down to 174mW. Hopefully, the resonant boost obtained will mean that the level isn't too far down (-3dB is expected for a sealed box). At 3kHz there's another peak (12.6Ω) so power is reduced to 636mW at the crossover frequency, possibly resulting in an audible dip at that frequency. When we get to 20kHz, the impedance is only 5.4Ω, so power is greater, at 1.48W.
To keep everything the same with 'pure' current drive (effectively infinite Z out), the current at 200Hz needs to be 508mA (close enough). This current will be forced into the system at any frequency, so at the woofer's resonance, the power is now 11.9W (ouch), at 3kHz it's 3.25W, and back down to 1.44W at 20kHz. It's fairly obvious that the result will not sound as it should. However, the bass boost and increase in 'presence' at 3kHz may give the impression of 'better' bass and treble. By using a modified impedance, it can be (almost) possible to maintain fairly consistent power regardless of impedance, but will that make the system sound any better?
According to a few articles on the Net, no-one should use voltage drive. This is a somewhat naive approach for a number of reasons, not the least of which is that everyone designs loudspeaker systems with the express intention that they will be driven by voltage amplifiers. Crossover networks are designed expressly for 'conventional' voltage amplifiers, as are the loudspeakers used in the enclosure. Multi-way systems (3-way or more) become something of a nightmare to design for a high impedance source, and an amplifier capable of very high output impedance (at least 10 times the highest speaker impedance at resonance) is also a difficult proposition. It can be done, but no commercial systems that I know of do so.
Once an impedance other than zero or infinity is used, the calculations become a great deal more tedious and the results are less predictable. Most of the time, performing said tedious calculations or simulating the results will not be useful, so it becomes either a subjective assessment or the results have to be measured. Unfortunately, the measurements are also tedious (and somewhat error prone unless you have an anechoic chamber handy). I'll save you the trouble - mostly, the answer is 'maybe'. With a system having a flatter impedance curve overall there will be an increase in bass output, and while a bass boost initially might sound 'better' (at least initially), usually it's not. Where a modified impedance can be most useful is when a system is biamped or triamped, with the modified impedance usually applied to the woofer and/ or midrange driver. This is easily done using the circuit shown below.
Lest anyone be misled by some on-line material, I suggest the following experiment. Disconnect the power amplifier from one of your speakers (the amp will, of course, be turned off). Lightly but sharply tap the woofer cone, and listen to the resonant sound of the decay. In some cases it will be more audible if you can place your ear near the vent (if applicable). Almost without exception, there will be a 'boomy' single note bass frequency that should be quite audible. Now, join the speaker terminals with a piece of wire and repeat the test. The resonant 'boominess' should be audibly reduced, indicating that the amplifier does indeed apply damping to the loudspeaker. It might not be as great as amplifier specifications claim, but the damping effect is almost always audible.
Because any current drive amplifier has a significant (non-zero) output impedance, it should be immediately obvious that without amplifier damping, the speaker will sound boomy. In some cases, you may even hear 'one note' bass with music - i.e. bass notes at the right frequency will be heavily accented, while other bass notes will be much quieter. This is not what we want to achieve, so the enclosure itself must be modified to include a great deal more damping material than otherwise to suppress the unwanted resonance(s). This can have some negative effects on the port tuning and box resonance (both of which are important for any tuned system).
Voltage drive is firmly established as the #1 method for powering loudspeakers. The drivers are designed and manufactured with that in mind, and the Thiele-Small parameters are invariably quoted with the assumption that the driver will be used with a conventional (voltage) amplifier. Where response correction is needed (whether for artistic or practical purposes), the most common methods are equalisers based on 'traditional' analogue techniques or (more commonly these days) digital, using DSP - digital signal processing. There's no real reason to think that using EQ will produce a result that's any different from an amplifier with a defined output impedance. Using a voltage amp with EQ retains the amplifier's damping of the speaker.
In most cases, speakers rely on at least some degree of acoustic damping provided by the amplifier, although for very high power systems that may run speakers in parallel with a combined nominal impedance of perhaps two ohms, amplifier damping is seriously curtailed by the resistance of the speaker leads. When high output impedance is used, the enclosures must be very well damped acoustically, because the amplifier provides no useful damping at all. The situation is different for guitar (and some other instrument amplifiers), where players prefer the added 'tonality' the speakers add when under damped. Many are accustomed to using valve (vacuum tube) amps, most of which have a relatively high output impedance because there's often very little negative feedback.
Since a large amount of negative feedback is used in nearly all transistor amplifiers, this reduces the open loop output impedance dramatically. Any amplifier with a high open loop gain and significant feedback reduces the intrinsic output impedance, and that's used in most amplifiers to create the low output impedance that's expected in the market. It's not uncommon for power amps to have Z out at the amplifier terminals (not including any wiring or connectors) to be less than 10mΩ.
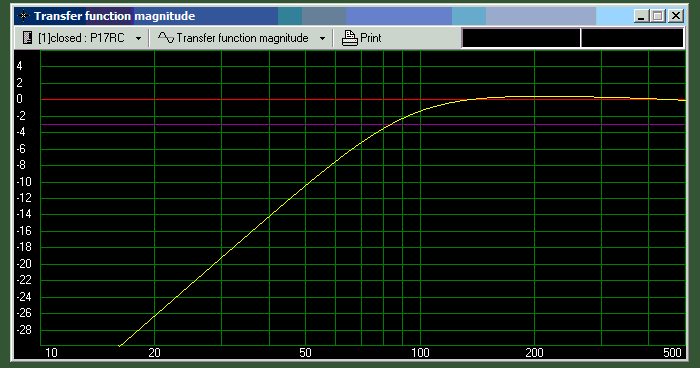
Figure 3 - Seas P17RC In 8 Litre Box (Voltage Drive)
The Seas P17RC driver was selected from the database of WinISD-Pro as an example only. The program will suggest a 10.62 litre box, but that can be reduced to 8 litres with very little change in the -3dB frequency. Unfortunately, the driver only manages to get to 80Hz in either enclosure, so a larger box is better. With voltage drive, that doesn't change the -3dB frequency at all, so the next thing to do is increase the source impedance. With 7Ω, there's a little peaking (+1.19dB at 110Hz), and the -3dB frequency is reduced to 60Hz - a useful improvement. Compared to room effects, the small peak is probably of little consequence (but this is for the designer to decide).
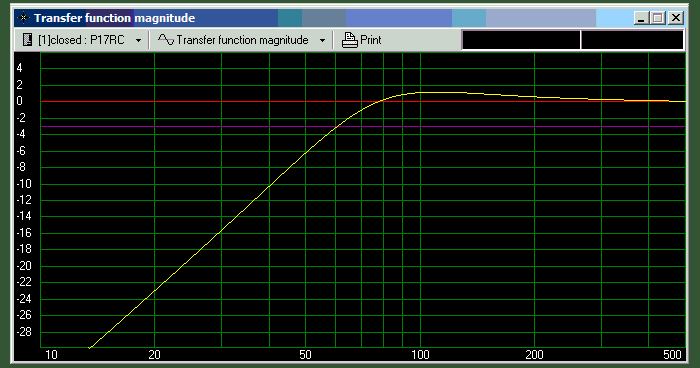
Figure 4 - Seas P17RC In 12 Litre Box (4 Ohm Drive)
The response with 7 ohm drive is shown above, with the enclosure increased to 12 litres. Because the amplifier provides little damping, the box needs to be well stuffed with appropriate material to ensure that there's little 'overhang' after a transient, but that's easily achieved and should be considered mandatory anyway to minimise internal reflections. The only thing to do now is arrange an amplifier that has an output impedance of 7Ω. By increasing the source (amplifier) impedance, the apparent voicecoil resistance is increased, which results in an increase of the electrical Q (Qes) of the driver. The effective increase of Qes means that the driver performs better in a larger box. However, the 'law of diminishing returns' strikes quickly, so to get down to 50Hz (-3dB) would require a 25 litre box and an amplifier impedance of 12Ω. This is impractical for a number of reasons.
For initial testing, it's easy to simply add a physical resistance in series with the amplifier's output. While this 'wastes' considerable power, it's an easy way to run tests so you can decide whether it's worthwhile to pursue the process to a modified impedance amplifier. The resistor needs to be at least 5W (10W is better if you use a large amp), and the power loss is not important if you are performing low-level listening tests and/ or measurements. By maintaining a reasonable stock of resistors in various values from 2.2 ohms up to perhaps 22 ohms, you can test the theory easily without making changes to the power amp. If you decide that 'elevated' output is advantageous, then you can run final tests with an amplifier with the selected output impedance. Remember that listening tests must be at the same SPL or the results will be skewed towards the configuration that's louder. SPL should be within 1dB overall, but if you can manage better that's preferable (0.1dB is generally considered the optimum level matching).
While the above shows the response with 7 ohms, it's (probably) better to limit the output impedance to around 4 ohms - at least for an initial test. Within reason, you can set up almost any impedance you like, and the exact value isn't particularly critical. Most loudspeaker drivers will have more variation than you'll get with an error of 0.5Ω or so.
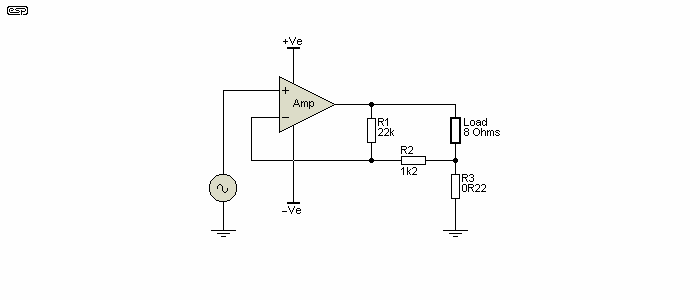
Figure 5 - Concept Four Ohm Output Impedance Amplifier
Mixed mode feedback component values must be determined to achieve the desired result. The values shown will achieve Z out of just over 4Ω, but there are practical issues that need to be addressed. The main one is that the 0.22Ω resistor has to be at least 2W and may run hot, so mounting it on the amplifier PCB might not be a good idea. Having it connected using wires isn't a good idea either, because if the connection from R2 to R3 is lost, the amp will almost certainly oscillate and may destroy itself. Most amplifiers (whether discrete or IC types) have a minimum gain that can be used, below which oscillation is likely. It's common that IC amplifiers in particular have a minimum gain requirement of 25dB (a gain of around 18), below which they are likely to oscillate. The Figure 5 circuit cannot achieve this (gain with an 8 ohm load is only 13).
To combat the gain problem, the feedback network has to be arranged so that the minimum gain is always present, regardless of the load's impedance. This is shown in several ESP projects, and the general form (arranged for 4Ω impedance) is shown in Figure 6. While the Figure 5 circuit works, it is not recommended for use with any power amplifier. The following version is tried and tested, and works properly with almost any power amplifier.
Z out = R3 × ( R1 + R2 ) / R2 (where R1, R2 and R3 are in the locations shown in Figure 5)
The above formula isn't especially accurate, but it does allow you to get a rough idea of the output impedance with different values. Figure 5 has a Z out of 4.4Ω based on the formula, but it's actually (almost) exactly 4Ω. While this may seem to be a large error, it's not really worth worrying about. A discrepancy of 10% is neither here nor there for the amplifier, because the speaker will have much greater errors.
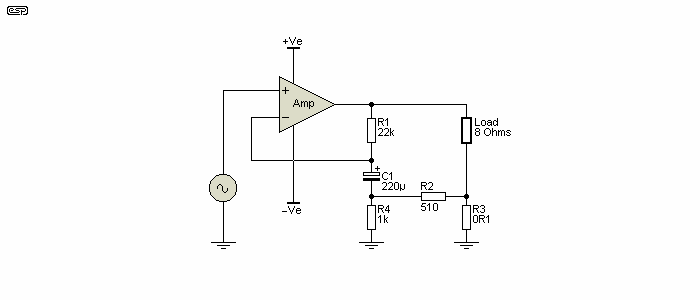
Figure 6 - Practical Four Ohm Output Impedance Amplifier
The practical version is a simple rearrangement of feedback resistances and the addition of a resistor and a capacitor. C1 is there so that the amp doesn't have a huge DC gain, which will cause problems. The value can be increased if you prefer, but the value shown gives a -3dB frequency of under 5Hz for output impedances of 4Ω or less. Up to 470µF will be necessary when R2 is less than 200Ω. R4 ensures that the amplifier has a nominal gain of 23 before the current feedback is connected. R2 is no longer critical, and if disconnected the amplifier works normally without oscillation. Unfortunately, a current amplifier (whether 'true' constant current or mixed feedback) is reliant on the load impedance, so setting the gain can be irksome with any biamped or triamped system. With the values shown, gain is just over 43 (32.7dB) with an 8 ohm load, but of course that changes as the speaker impedance varies with frequency. The minimum gain requirement is met easily, and can only be violated if the amp's load is less than 1.5Ω (not recommended for any amplifier).
Fortunately, it's easy to come up with a formula that comes close for this version, at least for output impedance - it's the same as shown above. Calculating the gain with no load is easy, but working out the gain with a load connected is a great deal more difficult. There are too many simultaneous voltages and currents that combine together to reach the end result, so it's easier to produce a table with different values for R3. This is (usually) the only value that needs to be changed, but even then the loaded voltage will always be different as the frequency is changed, because the amp's output impedance is non-zero and the loudspeaker load has an impedance that changes with frequency.
| R2 | Output Impedance | Gain - No Load | Gain - 8Ω Load |
| 100 Ω | 22 Ω | 243 (47.7 dB) | 65 (36.3 dB) |
| 120 Ω | 18 Ω | 206 (46.3 dB) | 63 (36 dB) |
| 150 Ω | 15 Ω | 169 (44.5 dB) | 60 (35.5 dB) |
| 180 Ω | 12 Ω | 145 (43 dB) | 58 (35.2 dB) |
| 220 Ω | 10 Ω | 123 (42 dB) | 55 (34.8 dB) |
| 270 Ω | 8 Ω | 104 (40 dB) | 52 (34.3 dB) |
| 330 Ω | 7 Ω | 90 (39 dB) | 49 (33.8 dB) |
| 510 Ω | 4 Ω | 66 (36.4 dB) | 43 (32.7 dB) |
| 680 Ω | 3 Ω | 55 (34.8 dB) | 39 (31.8 dB) |
| 1k Ω | 2 Ω | 45 (33 dB) | 35 (30.8 dB) |
For low impedances and especially if the load is 8Ω or more, it will be easier to use a series resistor to set the impedance. For example, if you only need a 2Ω output impedance, a wirewound resistor is a lot simpler than modifying the amplifier. While some power is lost across the resistor, it's generally comparatively low and won't be audible. For example, a 2Ω resistor in series with an 8Ω load and a 60W amplifier, the resistor would dissipate a bit over 12W (at full continuous power), and you'll 'lose' about 1.9dB. However, the amp's peak voltage swing around the speaker's resonant frequency is barely affected, and it's highly unlikely that you'll even notice the difference. Average power dissipation in the resistor won't exceed 5W with 'typical' programme material.
Note that the above table is approximate - there are small errors that are of little consequence with this approach. The values are close enough for most purposes, and if you are using particularly high impedances, a few ohms of difference is of no account. You can see that the unloaded gain becomes rather extreme for Z out above 10Ω, and the loaded gain may be higher than desirable as well. With a discrete amplifier this can be reduced with some circuit changes, but not with IC amplifiers.
Increasing the value of R4 reduces the gain (both with and without load) and has only a minor effect on the output impedance when it's greater than 10Ω or so. The effect of changing R4 is far more pronounced at low impedances, where R2 is also a comparatively high value. As noted earlier, gain must always be greater than the minimum specified for the amplifier. The suggested value of 1k ensures that the amplifier's gain can never be less than 23 (27dB), unless the load impedance is below 1.5Ω. That represents a fault condition that cannot be allowed to occur during operation. When Z out is greater than 10Ω, there is some 'wriggle' room to reduce the gain by increasing the value of R4. You will have to run tests to ensure that the gain doesn't fall below the minimum required and/ or that the amp remains stable (doesn't oscillate).
It's not hard to see why voltage drive is preferred - the amplifier gain remains the same regardless of the load impedance. With partial current drive (Z out > 0), the amplifier's gain depends on the load impedance, and the amp and speaker must be properly matched or the results are unpredictable. For instrument amps this isn't a problem, because it's just part of 'the sound', and speaker levels don't require matching as they do with a biamped system.
It must be considered that almost without exception, loudspeaker drivers and complete systems are designed based on the assumption that the amplifier has a low (less than 0.5 ohm) output impedance. If driven using current drive (full or partial), the result always sounds different, and because of extra bass (and usually treble), people often equate 'different' to 'better'. They are not equivalent, and the result is almost invariably worse, with uneven frequency response and poor low frequency damping. The only exception is if the speaker enclosure and amplifier are designed 'as-one', with the output impedance of the amplifier matched to suit the driver's performance.
Other than for instrument amplifiers (especially guitar and bass), once you decide to use a modified impedance amplifier it becomes an integral part of the loudspeaker. You can no longer mix and match amplifiers, because that will affect the system's response, as shown in Figures 3 and 4. If the speaker system was designed to be driven from a 4 ohm source impedance, the response (especially bass) will be adversely affected if a 'normal' amplifier is used.
From Table 1, the no-load voltage and 8Ω voltages are given. These voltages are measured across the output, and include the voltage drop of the series feedback resistor. Note that a resistive load is assumed, but a speaker has an impedance that varies with frequency. We'll use the values for a 510 ohm resistor as R3 in the formulae below. From this, we can calculate the exact output impedance from ...
I L = V L / R L (where I L = load current, V L = loaded Voltage and R L = load resistance) Z out = (V U - V L) / I L (where Z out = output impedance, V U = unloaded voltage, V L = loaded voltage) I L = 43 / 8 = 5.375 A Z out = (66 - 43) / 5.375 = 23 / 5.375 = 4.28Ω
I simply used the voltages (gain values) from the table, rather than any actual operating voltage. This makes no difference to the final result. You can subtract the value of R3 from the final result, but it's not worth the effort. Note that I have deliberately not developed a single formula to calculate impedance, because no-one will remember it. By showing the basic calculations (using only Ohm's law), it becomes easier to understand the process and remember the method used. An approximate formula to calculate Z out is shown above. According to this formula, Z out is 4.4Ω. This is not entirely in agreement with the results obtained above, nor with a simulation, but it will be more than acceptable for the normal range of desired impedances and it isn't complex. Results will be within a few percent of the theoretical value, which is more than good enough when dealing with speakers.
So we have created an amp with an output impedance of 4.28Ω, with very little loss. Just over 0.5W is lost in the 0.1 ohm series feedback resistor with 50W output into 8Ω, but you must use at least a 2W (wirewound) resistor so it can handle the current. To see if this is useful, we will now have a look at what happens when the load impedance doubles or halves.
With a 16 ohm load, the power into the load falls to 36W, or about -1.4dB. Contrast this with the conventional low impedance amp whose power will fall to 25W (-3dB or half). When the impedance is reduced to 4Ω, the output power is now 56W (an increase of 0.5dB), while a conventional amp would be producing 100W - an increase of 3dB.
There is no magical impedance that will give the same power into any load from double to half the nominal, but about 4Ω for a nominal 8 ohm system comes close. I am not about to test all possibilities, but having experimented with the concept for many years I am quite convinced that there are practical benefits to the use of modified current drive, where the impedance is defined. The exact impedance will depend to a very large degree on just what you are trying to achieve. It's not a panacea for anything of course, but it can be used to advantage when applied properly.
Measuring the output impedance is easy, at least when it's 4Ω or greater. With no load, apply a sinewave input, and set the level to something convenient (e.g. 8V peak-peak with fits on a scope screen nicely). Next, apply a load that's around the value you expect for output impedance. The level should drop to exactly half when the load is connected. For example, look at the values for an 8 ohm impedance in Table 1. With no load, the gain is 104, falling to 52 with an 8 ohm load - output impedance is therefore 8Ω.
It's harder when the designed output impedance is low (less than 4Ω), because you risk damaging the amplifier with very low load impedances. It can still be done, simply by reducing the input level so the output is (say) 80mV peak-peak. This ensures that amplifier output current is low - about 28mA with an output of 80mV, so the amp will not be damaged. The alternative is to use the rated load impedance and run some calculations to determine the output impedance, using the formulae shown above.
An important point needs to be made regarding amplifier clipping. When an amplifier's output voltage attempts to go beyond the power supply voltages, the amplifier is clipping (cutting off) the waveform peaks, and all forms of feedback are inoperable. Feedback (whether voltage or current) relies on the amplifier remaining within its linear range at all times. A current drive or mixed mode amplifier cannot provide more current or voltage than it's designed to provide to the load, and if the maximum current is exceeded the amplifier may be destroyed. Exceeding the linear voltage range simply results in clipping, and the output is limited by the supply voltage - current drive is inoperable with an overdriven amplifier.
It has been suggested that loudspeaker intermodulation distortion is dramatically reduced by using a high impedance source [ 1 ]. One site I looked at some time ago was Russian, and a reader sent me a translation. I have experimented with this idea to some extent, but have been unable to prove that this is the case - at least with the drivers I tried it with.
This does not mean that the claim is false, but I am unable to think of any valid reason that could account for such driver behaviour. It is interesting anyway, and some of you might like to carry out a few experiments of your own. I would be most interested to hear about your results should you decide to test this theory. It's worth remembering that with no exceptions I can think of, loudspeaker drivers are designed for (and tested with) as close to a zero ohm source impedance as possible. All commercial speaker systems are designed to be fed with a normal low impedance power amplifier, because that's considered the 'ideal' case and virtually all commercial hi-fi and sound reinforcement amps are designed for (very) low output impedance.
By adjusting the impedance of an amplifier, the total Q (Qts) of a loudspeaker can also be altered, so driver behaviour in a given sized box can be changed. This can be used to adapt an otherwise unsuitable loudspeaker to a speaker enclosure, but it does have limitations in terms of the overall variation that can be achieved.
More variation can be achieved by virtue of the fact that it is now possible to either retain or increase the power delivered to a loudspeaker at (or near) resonance, so that the ultimate -3dB frequency may be lowered from that theoretically claimed for a loudspeaker/ enclosure combination. Care is needed, since too much additional power will make the speaker boomy, and usually additional internal damping material is needed to compensate for the minimal damping factor provided by the amplifier. With the amplifier output impedance set at 4Ω, damping factor into an 8 ohm load is 2 - a far cry from the figures of several hundred typically quoted. These (of course) fail to take into consideration the resistance of the speaker leads, and loudspeakers themselves are usually compromised by the crossover network, so the damping factor figure is not always as useful (nor as high) as it might seem.
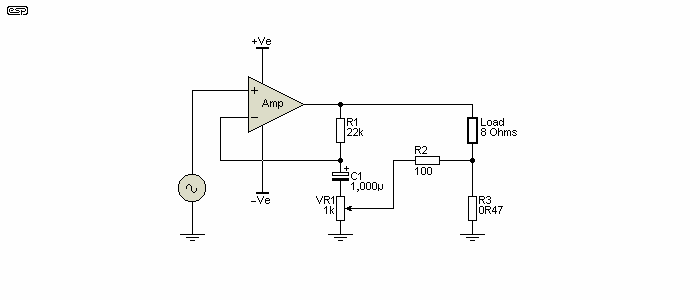
Figure 7 - Variable Impedance Amplifier
The version shown above has variable impedance. It can be varied from (close to) zero ohms when the pot wiper is at ground, up to 100Ω with the pot at maximum. Be warned that the gain varies as the pot value is changed, although the variation isn't overly dramatic for most of the range.
The results of using modified impedance can be very satisfying, allowing a useful extension of the bottom end. My own speakers are driven from a 2 ohm amplifier impedance, and there is no boominess or other unpleasantness (the enclosures are exceptionally well damped), but a worthwhile improvement in bass response is quite noticeable for the woofers, and the midrange drivers would otherwise have a slight droop at 300Hz (the crossover frequency between the woofer and midrange).
Partial current drive can also be used with vented enclosures. Care is needed because they are more sensitive to the actual output impedance of the amplifier, but it's well within the abilities of anyone who chooses to experiment to it try out for themselves. WinISD-Pro is very handy for this, as it offers the ability to select the source impedance, something that the standard version doesn't provide. Using the same driver as shown above (Seas P17RC) in a 35 litre box, tuned to 35Hz and with a 3Ω source impedance, the response extends to 35Hz (-3dB) or 42Hz at the -1dB point. That's not bad for a 170mm diameter driver, and it would satisfy many listeners.
It's worthwhile to reiterate the comments made in the Project 56 article about power compression in loudspeakers. This is a natural phenomenon that causes loudspeaker drivers to lose efficiency as the voicecoil heats up, and while it's generally considered a nuisance, it may be the only thing that prevents driver failure in a system that's pushed to the limits. Consider a speaker driver rated at 1,000W - very silly, but they exist in great numbers. If operated with a 1kW amplifier, the average power might be around 500W - assuming some clipping, and heavy signal compression at the mixer output.
After a short while, the voicecoil heats and its resistance rises, so less power can be absorbed from the amplifier. 3dB power compression is considered to be quite good (see Loudspeaker Power Handling Vs. Efficiency for more details), so the actual average power will drop to around 250W. There is one detail that it's worthwhile remembering ...
Power compression may well be the only thing that saves the speaker from failure!
As the voicecoil heats up, the power is reduced, and that alone prevents the temperature from continuing to rise until the voicecoil fails or sets the cone on fire. If the amplifier were to have current drive (and sufficient reserve power - aka 'headroom'), the power will increase as the voicecoil gets hotter, ensuring the demise of the loudspeaker. For this to be 100% effective at destroying the speaker, the amp's output impedance has to be somewhat higher than the speaker's impedance (at least 6Ω for a 4Ω driver).
Ultimately, the amp's supply rails limit the maximum power that can be delivered, but there are plenty of amps that are capable of destroying any loudspeaker ever made - especially very high power Class-D amps. It's probably fortunate that it's often somewhere between inconvenient to impossible to convert some Class-D amps to current drive without serious modifications.
Power compression is very real, and if you do anything to 'compensate' (such as using a bigger amp and turning up the volume) driver failure is almost a certainty. Equipping amplifiers with partial current drive would be an excellent way to guarantee driver failures, because the voicecoil self-heating cannot protect the system from excess temperature. Unfortunately, the use of negative impedance has too many other problems, so it can't be used to help protect the drivers.
The effects of voicecoil temperature (and therefore its resistance) also have implications for a passive (inductor and capacitor) crossover network. As the voicecoil resistance rises, so too does the impedance of the speaker, and passive crossover networks have to be designed to match a particular impedance. When the impedance changes, so does the crossover frequency and filter alignment, leading to response anomalies when a system is pushed to its limits. This does not occur with active crossovers of course, but level differences between drivers can (and do) change unless all of the voicecoils are at the same temperature. To say that this is unlikely is serious understatement.
Note that positive output impedance is very common for guitar (and to a lesser extent, bass) amplifiers, but they are traditionally equipped with speakers that can handle the full output power when the amp is driven into hard clipping, so the output impedance cannot create a situation where the speakers get more power than they can handle safely. It's used as a tonal modifier, allowing the speakers to provide their own colouration to the sound, and is simply an extension of the situation with valve ('tube') amps, most of which have comparatively high output impedance.
There is the potential for power compression to introduce distortion, due to the heating and cooling of the voicecoil. However, this is a relatively slow process (seconds rather than milliseconds), and will not usually generate significant audible distortion, even at the lowest frequencies of interest (below 25Hz). While I have no doubt that it could be measured if one were so inclined, attempting to eliminate (or mitigate) it would be a big mistake for the most part. As already stated, power compression may be the only thing that saves high power loudspeakers from destruction, although using current drive at 'sensible' power levels is unlikely to cause any harm. 'Sensible' in this context means an average power level of perhaps 5-10 watts, implying peak levels of up to 50-100 watts (calculated by voltage, and assuming that the voicecoil's impedance is the nominal value).
With all this info, it would be remiss of me not to include a proper current (aka transconductance) amplifier. They aren't trivial, and the circuit shown does not include complete details of the amplifier itself. The main addition is the DC servo circuit (U1), which is essential to keep DC out of the speaker. Use of a feedback coupling capacitor isn't practical because of the extremely low impedance of the feedback network, which would require an unrealistically large value capacitor. Even the DC servo needs to have a very slow response, simply because the output impedance is very high and unwanted interactions will occur.
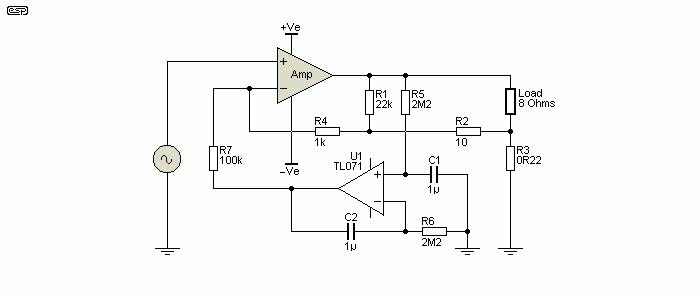
Figure 8 - High Impedance Amplifier
The DC servo can't simply be connected to the feedback point either, because without R4 in its new location, the impedance is too low for the opamp to be able to correct any DC error. By using R4 and R7, the opamp can deliver just enough current to pull typical DC offsets (up to 1V or so at the output) back to something less than a couple of millivolts. The output impedance is about 500 ohms - not exactly infinite (as required for 'ideal' current drive), but it's an order of magnitude greater than the typical maximum impedance of a loudspeaker load. If R1 is deleted (meaning that you can also delete R2), Z out increases to over 8kΩ, but there is no reason to expect that this will be beneficial.
You also face some difficulties trying to build an amplifier with an open-loop gain (without load) that may exceed 60 thousand (8kΩ Z out), while retaining flat open loop response and stable operation when loaded. These are not insignificant undertakings, and expecting an off-the-shelf power amp IC to provide good results is wishful thinking at best. The design of an amplifier that satisfies all of the criteria for true current output is daunting, simply because achieving very high output impedance is, to put it mildly, a serious undertaking.
There are some suggested circuits in the second reference, but they are not trivial. The article covers the salient points, and specifically mentions the difficulties involved. It's unknown if anyone other than the authors have built amplifiers using the circuits shown, but be aware that it's a fairly old document and some of the suggested devices may be obsolete or difficult to obtain. It's also important that the final amplifier can not only deliver the current demanded by the load (loudspeaker), but also has sufficient voltage to accommodate the peak voltages, which may be far greater than are typically provided by a voltage amplifier.
It is too easy to make a change such as shown here, and fully believe that the result is an improvement, where in reality (as eventually discovered after extensive listening and comparison) the opposite is true. Positive impedance can produce an improvement in bass response, but the cost can be high - boomy, over-accentuated bass around resonance, usually accompanied by a loss of definition. There will be more freedom for the speaker cone to waffle about after the signal has gone ('overhang'), and it is rare that a speaker driven by a higher than normal impedance will perform well without additional damping material in the enclosure.
There is no doubt that at output impedances in the order of 4 to 6Ω your amp will sound more like a valve amp (but generally with lower distortion), but it is up to you to decide if this is what you really want to do. The technique works well for guitar amps, as it allows the speaker to add its own colouration to the sound, which adds to the overall combination of distortion and other effects to produce pleasing results. For Hi-Fi the case is less clear, and experimenting is the only way you will ever find out for sure.
However, you will need to take great care to avoid inadvertent bias towards one scheme or the other. This is sometimes known as the 'experimenter expectancy effect', in that the experimenter expects to hear a difference, and due to subconscious bias will hear a difference, even if the outcomes are actually identical. There is no known cure, and even the most experienced people (who already know about the effects of subconscious bias) will be caught out anyway. Getting around it with loudspeakers is particularly difficult, because the DBT (double-blind test) methodology is very difficult to implement with large physical enclosures that have to be in the same location so that room effects don't affect the outcome.
I'm unsure just how you can avoid this effect for listening tests, but if careful measurements are used they are a more reliable way to determine whether a loudspeaker/ system is better or worse. This doesn't consider the psycho-acoustical phenomena that influence 'the sound' of any speaker system though, and this is one place where measurements may not coincide with listener preferences. The references show measurements that indicate lower levels of speaker intermodulation distortion, but that doesn't actually mean that the speaker sounds better. Many of the measurements described seem to have been taken at (IMO) unrealistically low power levels, so correlation with listening tests (using music) may not be as great as hoped for.
Much of the info here is similar to that shown in Project 56 and some parts are duplicated (deliberately). I have added more details so the info presented is easier to use, and it is intended to be a starting point for experimentation. The circuits shown will all work with 'real' amplifiers, but great care and considerable testing are needed to ensure that the results you actually obtain are providing a real benefit. Be very careful if you use IC power amps (LM3886 or TDA7293 for example). Most are designed to run at a particular minimum gain, and they may oscillate if the gain is reduced below the minimum recommended due to the current feedback. This is especially dangerous if the load impedance falls at high frequencies.
There have been many claims over the years that current drive is the best, and some may claim it's the only) way to drive loudspeakers, as it reduces distortion and allows the speaker to work the "way it was intended". While there is some discussion of this on the Net (see [ 2 ] as an example), there is little real evidence that the benefits are anywhere near as great as claimed. Tests I've run have shown little improvement, and this is expected given that loudspeaker systems and the drivers used therein are designed specifically with the understanding that they will be driven with a voltage amplifier. By definition, that means the output impedance is low, always below 0.2Ω, and often much less.
A claim that you may see is that current drive eliminates power compression in loudspeaker drivers, because the change of voicecoil resistance doesn't affect the amplifier current. While this is perfectly true, in reality as the voicecoil heats you may actually get more power with pure current drive, thus pretty much guaranteeing that the driver will be destroyed without human intervention. This can be mitigated by using modified impedance, but why? The reduced power delivered to speakers when they get hot is often the only thing that saves them from destruction, and current drive ceases as soon as the amplifier clips anyway.
Naturally, there are a great many outrageous and/ or poorly thought through claims made by the ever present audio nut-cases - 'new' and 'revolutionary' are but two of the silly terms used to describe what they think they have found. Well, sorry chaps, it was actually never lost, it's anything but new, and isn't even a little bit revolutionary. Discoveries in this area are pretty much old-hat now, because so many people have played with current drive for so long.
Many full-range loudspeakers are likely to sound better with current drive (extended bass and treble in particular), but cabinet size, internal damping and (more than likely) parallel filters have to be optimised to account for the loss of amplifier damping and to minimise peaks and/ or excessive high frequency output. Using mixed mode amplifiers can allow a speaker to work at its best in a larger than optimal enclosure, because the use of a defined source impedance affects the Thiele-Small parameters.
It is also possible to adapt a bridged amplifier to use current drive, but there are some interesting obstacles to overcome. This will not be covered here unless there is overwhelming interest. In particular, the problem of ensuring a high gain with good frequency response remains, and maintaining stability at the lowest gain (coincident with the lowest impedance of the speaker driver) is difficult to achieve, especially for an amplifier that's expected to cover the full audio range. This becomes even harder if the output impedance is more than 100Ω.
I've been using current drive in various forms since the early 1970s, with typical output impedances (at low frequencies) of up to 200Ω. Over the years many people have heard what they initially thought were huge improvements in the sound of individual drivers and/or complete systems. In reality, only some effects were ultimately found to be useful, and almost identical results can often be achieved with fairly basic equalisation. This doesn't negate the process though, and there are some who think that current drive is worthy of taking out a silly patent on a process that is already well known to a great many people, and for a very long time.
For myself, I still like playing around with variable impedance. I have a 3-way active test amplifier with two channels that can be varied from -8 to +32Ω, and I use it regularly - it drives my workshop 3-way active sound system. It has been used in the past to test many, many drivers, enclosures and compression drivers + horns, and it remains a useful tool for testing, despite its age (it was built sometime in the 1980s!).
Useful tool, major improvement in loudspeaker driver performance or just a fun thing to play with? I leave it to the reader to decide. 
 Main Index
Main Index
 Articles Index
Articles Index